Методика расчета сферических куполов на прочность и устойчивость

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2023PNRPU MECHANICS BULLETIN

Оболочечные конструкции широко применяются в различных областях промышленности [1–5], в том числе и в строительстве для покрытия большепролетных сооружений. Наиболее часто используемый вид геометрии таких конструкций – сферическая оболочка (купол), исследованию процесса деформирования которой посвящено достаточно много работ [6–16].

Сферические оболочки применяются для решения различных прикладных задач [8; 12; 17–20] и исследуются как при статических воздействиях [14, 21–23], так и при динамических [11; 13; 17; 24–28]. Например, процесс деформирования оболочки при действии равномерно-распределенной нагрузки исследуется в работах [12; 23; 26; 28; 29].

Оболочечные конструкции могут быть выполнены как из изотропных [27; 29–32], так и из ортотропных материалов [25; 30; 31].

В работах [9–13; 29] рассматриваются оболочки при жестком закреплении контура, а в работах [10–14; 26; 31; 32] – при шарнирно-неподвижном. Влияние несовершенств конструкции на процесс ее деформирования исследуется в работах [21; 24; 26]. Прочность анализируется в работах [7–9], а устойчивость – в работах [14; 21– 23; 27; 28; 33].

Математическая модель Кирхгофа – Лява используется в [9; 26; 30], а модель Тимошенко – Рейсснера – в работах [10; 27; 30; 31; 33].

В работе [21] показана важность учета нелинейности процесса деформирования оболочек из текстильно усиленного бетона (TRC). Помимо геометрической и физической нелинейности, рассматривается учет несовершенств и показано существенное снижение значения критической нагрузки при их наличии.

Tornabene et al. [32] проведен анализ свободных колебаний однослойных и многослойных изотропных композитных сферических оболочек. Показано сравнение между классическим и усовершенствованным методами GDQ и точным трехмерным решением.

В работе [15] рассмотрена математическая модель, позволяющая определять напряжённо-деформированное состояние сферической оболочки из титанового сплава ВТ1-0, внешняя нагрузка принята поперечной равномерно распределённой, действующей на внешнюю поверхность, среда принята действующей на внутреннюю поверхность оболочки. Получены нелинейные разрешающие уравнения расчёта сферической оболочки. Разработан алгоритм решения задачи наводороживания оболочек из титанового сплава.

Исследование нелинейного деформирования тонкостенных конструкций приводит к необходимости решения нелинейных систем уравнений. Основная сложность таких систем заключается в неустойчивости решения вблизи особых точек, соответствующих критическим нагрузкам, и возможности ветвления кривой равновесных состояний, то есть появлении точек бифуркации. Существует группа численных методов, позволяющих получать все точки кривой равновесных состояний (в отличие, например, от метода Ньютона), – это методы, основанные на продолжении решения по параметру. К ним следует отнести и метод последовательных нагружений, предложенный В. В. Петровым [34], и метод продолжения решения по наилучшему параметру, детально описанный В.И. Шалашилиным и Е.Б. Кузнецовым [35].

Данная группа методов позволяет находить верхние и нижние критические нагрузки потери устойчивости оболочек, исследовать их закритическое поведение [36–40].

Целью данной работы является расширение области применения разработанных авторами моделей, алгоритмов, программного обеспечения и методик исследования оболочечных конструкций на сферические купола.

1.    Теория и методы 1.1.    Математическая модель деформирования сферической оболочки

6 1 =

£ W

A 8 x

+ k x U I , 6 2

k_x = —, k_y ^xR 1 ^y

^^^^^^B

£ W

B 8 у

+ k y V

R 2

Будем рассматривать сферические оболочечные конструкции толщиной h и радиуса R (рис. 1), шарнирнонеподвижно или жестко закрепленные по контуру и находящиеся под действием внешней равномерно распределенной поперечной нагрузки q . Нагрузка направлена по нормали к срединной поверхности.

где £ x , e y - деформации удлинения вдоль координат x , у срединной поверхности; y xy , Y _xz , Y y_z — деформации сдвига в плоскостях x О у, x О z , у О z ; U = U ( x , у ) , V = V ( x , у ) , W = W ( x , у ) – неизвестные функции перемещений; Т _x = Т _x ( x, у ) , Т _у = Т _у ( x, у ) - неизвестные функции углов поворота нормали. Данные соотношения являются универсальными и могут использоваться для оболочек разного вида посредством указания нужных параметров Ламе и радиусов главных кривизн.

Геометрические соотношения для слоя, отстоящего на расстояние z от срединной поверхности, выражаются следующим образом:

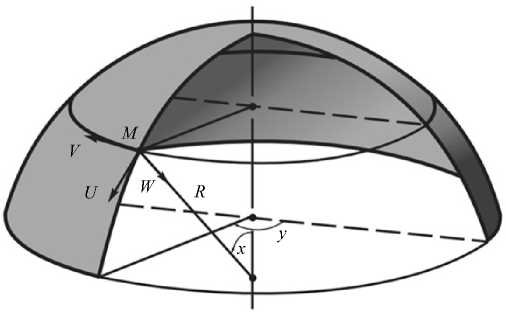
Рис. 1. Сферическая оболочка

Fig. 1. Spherical shell

£ x = £ x + Z X1, £ у = £ у + Z X2, Y Xy =Y xy + 2 z X12"    (2)

Функции изменения кривизн х 1 , Х ₂ и кручения х ₁₂ для принятой модели принимают вид:

X1 =

1 5Т 1 8Л_т       1 ^дТ у 1 5 в_и,

--- + Т,. X2 = - +--т

A 8 x AB 8 у ^у      B д у AB д x

^X 12 = 2

1 ат у 1 ат x 1 ГаAw abvi Г +1     Т x + Т у I

A d x B д у AB (д у     d x    )

Функционал Лагранжа полной потенциальной энергии деформации оболочки, находящейся под действием механической нагрузки, является суммой работ внутренних и внешних сил, и для модели Тимошенко – Рейсснера принимает следующий вид:

Для сферической оболочки с радиусом R параметры Ляме принимают вид A = R , B = R sin x , главный радиус кривизны R = R 1 = R ₂ = const. Будем рассматривать геометрически нелинейный вариант модели, учитывающий поперечные сдвиги. Тогда геометрические соотношения в срединной поверхности оболочки принимают вид

ab

Е = - bV£ + Ne +-(N +N )у +

5 2 x x у у 2 xy ук I xy a1 0

⁺ Mx X 1 ^{+ М} у X 2 ⁺ ( ^М ,у ⁺ M_y x ) X 12 ⁺

+ Q x ( Т x -6 1 ) + Q_y ( Т у -0 2 ) -

- 2 1 P_xU + P y V + qW I^ ABdxdy .

£x = x	1 a и 1 a a --+— v— a a x ab а у	- kxW + 1 x 2	0 12 ,
£ у =	1 a v 1 t b в + и в а у ab a x	- kW + 1 y 2	0 22 ,	(1)
Y x, =	1 a v 1 а и -          +             - a a x в а у	—U ^ A - ab а у	— V ^ B + 0!02 , ab a x 12

Y xz = k f ( z ) [ Т x -0 1 ] , y _yz = k f ( z ) [Т у -6 2 ] ,

В дальнейшем будем рассматривать только поперечную компоненту нагрузки q , то есть P _x = Р _у = 0.

Несмотря на то, что все рассуждения для удобства

интерпретации представлены в размерных параметрах, в разработанной расчетной программе все вычисления выполняются в безразмерных [41]

x ^- а      у _т aA

^ = -----, П= ”, Х= —, k,. = hkx, kn= hky , a - a,       b bB

и = U- , V = bVB , W = W h 2 h 2 h

Y aA Y bB xy x h , y h

a ⁴ A ⁴ q       aA bB

P = —2—-, A = —, B =— h ⁴ E ₁    hh

z z = —.

h

Это позволяет выровнять в системе уравнений порядок неизвестных переменных (что повышает устойчивость вычислительного процесса) и получить данные сразу для большого числа подобных оболочечных конструкций (рис. 2).

Рис. 2. Подобные сферические оболочки

Fig. 2. Similar spherical shells

1.2. Алгоритм решения

При исследовании напряженно-деформированного состояния оболочки решается вариационная задача нахождения минимума функционала. Для этого к функционалу (4) применяется метод Ритца, и для решения задач в размерных параметрах представим искомые функции в виде

NN

U ( x , y ) = ZZ U ki X 1 Y 1 l , = 1 l = 1

V (x, y) = Z Z VkiX2^2, W (x, y ) = Z Z WkiXkY, k=1 l=1

k = 1 l = 1

NN тД x, y )=     y HxYy;, xxkl44

k = 1 l = 1

NN yy (x, y )=ZZy yklXY, k=1 l=1

где U.., V., W.., T.w, T ., - неизвестные числовые коэф-kl kl kl xkl ykl фициенты, а X1k–X5k, Y1l– Y5l – известные аппроксимирующие функции аргументов x и y , удовлетворяющие заданным краевым условиям на контуре оболочки, N – количество членов разложения. В соотношениях (6), чтобы предусмотреть все возможные сочетания выбранных аппроксимирующих функций Xk, Yl, общее количество слагаемых должно соответствовать правилу N = n2, где n - целое положительное число.

Расчет сферических куполов требует выбора специальных аппроксимирующих функций вдоль оси x (безразмерная ось ^ ), поскольку необходимо избежать особенности в вершине купола. В связи с этим область конструкции будем определять в пределах от - а до a , притом функции возьмем в виде

X k = X k = X k = X k = sin I k п x + a I , 1235

V k I, x + a I

X4 = cos I kпI

V

А вдоль окружной координаты аппроксимирующие функции для куполов должны удовлетворять условию периодичности, поэтому возьмем их в виде

Y l = Y ₂ l = Y ₃ l = Y 4 l = Y 5 l = 1, cos I 2 п y I , V b )

■ I      y I        I ,   y I       I  , y I sin 2n , cos 4n , sin 4n .

V    b J     V    b )     V b )

Здесь функции вдоль окружной координаты задаются не зависимостью от l , а берутся в виде ряда. И в безразмерном виде получим

X k = X ₂ ^k = X ₃ ^k = X ₅ ^k = sin ¹ k n^+ 1

X^k = cos| k п-^— I, ⁴ V 2 )

Y l = Y2 l = Y3 l = Y4 = Y5 l = 1, cos (2nn), sin(2nn), cos(4nn), sin(4пп).

В случае жесткого закрепления для сферических куполов необходимо взять

Xk = X2k = X3k = X44 = X5k = sin I kп x+a I,(10)

V lllll

1 Y 2 Y 3 Y 4 Y 5

, I y I • y I I „ y I I „ y I = 1, cos 2п— , sin 2п— , cos 4п— , sin 4п— , 7                            7                            77

V b ) V b ) V b ) V b )

kkkkk

X 1 = X 2 = X 3 = X 4 = X 5

I ^+11 = sin k п

V 2 )

lllll

Y 1 Y 2 Y 3 Y 4 Y 5

= 1, cos ( 2 nn ) , sin ( 2 nn ) , cos ( 4 nn ) , sin ( 4 nn ) .

Получаемая в итоге система нелинейных алгебраических уравнений решается методом продолжения решения по наилучшему параметру (в качестве наилучшего параметра берется длина дуги кривой равновесных состояний в пространстве неизвестных коэффициентов). Получаемые в процессе использования метода задачи Коши решаются методом Эйлера.

В качестве критерия потери устойчивости оболочек будем использовать критерий А.А. Ляпунова: нагрузка, при которой малому изменению нагрузки соответствует существенное изменение прогиба, считается критической нагрузкой. Практически строится кривая «нагрузка q – прогиб W » в какой-то характерной точке конструкции, например, в центре оболочки.

При использовании алгоритма, основанного на методе Ритца и методе продолжения решения по наилучшему параметру, экстремумы кривой в пространстве состояний (соответствующие критическим нагрузкам) определяются из условия det( J ) = 0 .

Следует отметить, что при использовании метода продолжения решения по наилучшему параметру обход особых точек не требует смены параметра и происходит автоматически, данный процесс детально описан в [42].

Однако следует также отметить, что величину шага по длине дуги кривой равновесных состояний следует выбирать адаптивно. Чем больше разница между векторами приращений числовых коэффициентов, тем менее устойчив вычислительный процесс и больше погрешность решения. Поэтому на каждом шаге решения вычисляется угол между векторами приращений с прошлого и текущего шага, и если значение угла превышает заданный параметр точности А а 1 , то происходит возвращение процесса на шаг назад и расчет нового вектора уже с уменьшающим его длину коэффициентом А a k . Предлагается брать коэффициент А a k = 1/ 2 .

Также здесь вводится и второе ограничение по углу, значение которого А a ₂ берется в два раза меньше, чем первое установленное ограничение ( А а ₂ = А a 1 /2). В том случае, если значение угла находится в диапазоне между этими двумя значениями А a 1 и А а ₂, то выбранный коэффициент при следующем шаге принимается А a k = 1. А если значение угла меньше А а ₂, то на следующем шаге А a k = 2 .

Такой подход позволяет исследовать прочность и устойчивость оболочек, обходить особые точки кривой «нагрузка – прогиб», получать значения верхней и нижней критических нагрузок, находить точки бифуркации и исследовать закритическое поведение конструкции [42].

2.    Расчеты

В данном параграфе приводятся результаты исследования прочности и устойчивости замкнутого сферического купола, что показывает возможность применения разработанной математической модели, алгоритма и программного обеспечения для исследования конструкций данного вида.

Для расчета сферических куполов будем использовать аппроксимирующие функции (9), (10).

Для верификации предложенного подхода проведем сравнение результатов исследования устойчивости сферической оболочки (купола) с решением, полученным Э.И. Григолюком и Е.А. Лопаницыным [43]. В этой работе рассматривался сферический пологий купол, жестко закрепленный по контуру и находящийся под действием равномерного поперечного давления с параметрами R / h = 100, углом разворота a = 19° = 0,3316 рад, материал оболочки - сталь с E = 2,1-105 МПа, ц = 0,3. Также авторами вводится параметр тонкостен-ности оболочки ц = [12 (1 -ц2)]4 [ a2 Rh ]2 = 6.

Э.И. Григолюком и Е.А. Лопаницыным для описания процесса деформирования купола используется уравнение Маргерра в осесимметричной постановке (учитывается геометрическая нелинейность и поперечные сдвиги в радиальном направлении). Решение этих уравнений строится методом Релея – Ритца с аппроксимацией радиальных перемещений и прогиба купола суммами по функциям Бесселя. Решение системы нелинейных алгебраических уравнений, получающееся методом Ре-лея – Ритца, ищется методом продолжения решения по наилучшему параметру (длине дуги равновесных состояний). Для оценки результатов вводится безразмерный 1

параметр нагрузки q * = [ з ( 1 - ц ² ) ] ² [ qR 2/2 Eh ² ] и безразмерный параметр прогиба w * = W / h .

В работе [43] для данного примера получено значение критической нагрузки q * r = 0,972 , потеря устойчивости происходит хлопком. Глубина вмятины вблизи вершины купола w ₀ ^* наибольшая, и плавно понижается к контуру купола. До потери устойчивости величина прогиба составляла w * = 0,49, после потери устойчивости он становится равным 10,55 (рис. 3).

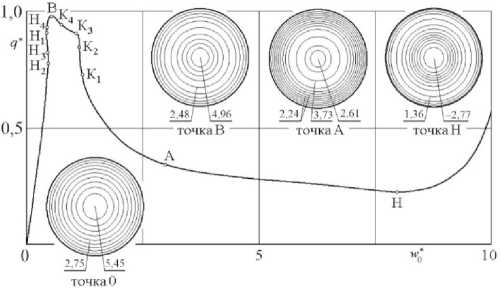
Рис. 3. Траектория нагружения в случае осесимметричного деформирования рассматриваемого купола [43]

Fig. 3. Loading path in the case of axisymmetric deformation of the considered dome [43]

В нашем случае при аппроксимации всех неизвестных функций вдоль окружной координаты рядом

• 1,    cos ( 2 nn ) , sin ( 2 nn ) , cos ( 4 nn ) , где n = — , были полу-2 п

чены значения критической нагрузки, показанные в таблице.

Сравнение полученных значений критических нагрузок

Comparison of the obtained values of buckling loads

N	Шарнирно-неподвижное закрепление				Жесткое закрепление
	Прочность	Устойчивость			Прочность	Устойчивость
	q pr , МПа	P	q cr , МПа	q c * r	q pr , МПа	P	q cr , МПа	q c * r	q c * r [43]
4	4.29	168.99	29.35	1.155	2.27	117.44	20.39	0.802	0.972
9	4.48	125.62	21.82	0.858	3.39	107.67	18.70	0.735
16	4.50	114.08	19.81	0.779	3.38	131.13	22.78	0.896

Будем рассматривать сферический купол и при жестком закреплении, и при шарнирно-неподвижном. Для сравнения результатов, полученных автором, значения критических нагрузок также дублируются с переводом в параметр q _c ^* _r . Для тестовой задачи разница в значениях составила около 7 %. Однако более низкое значение критической нагрузки лучше согласуется с результатами экспериментов, также описанными в работе: согласно экспериментам, диапазон q _c ^* _r составляет от 0,28 до 0,9. Кроме того, данное расхождение может быть объяснено использованием разных математических моделей и выбранными параметрами точности численных методов.

На рис. 4 показан график «нагрузка – прогиб» для рассматриваемого варианта купола при разных значениях N , совмещенный с графиком из работы [43]. Из рисунка видно, что при N = 16 кривые уже достаточно хорошо согласуются.

На рис. 5 показан исследуемый сферический купол в недеформированном состоянии в докритический момент и в закритический момент. Помимо фрагмента поля прогибов и его вида сбоку (в безразмерных параметрах), показано изображение купола в глобальной декартовой системе координат (в размерных параметрах).

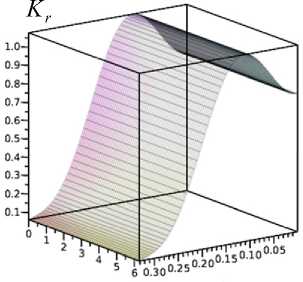
Также для рассматриваемого купола была проведена оценка невыполнения условий прочности. Оценка производилась по критерию Мизеса: на рис. 6 показаны поля критерия и соответствующие им нагрузки при разных значениях N . Учитывая, что для данной конструкции начало невыполнения условий прочности произойдет до потери устойчивости, может быть рекомендовано для ее проектирования выбрать марку стали с более высоким значением предела текучести.

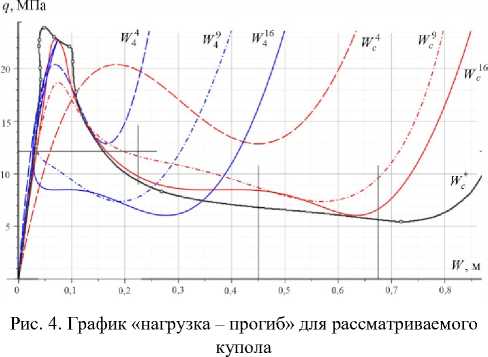
Fig. 4. Graph load – deflection for the considered dome

Заключение

Сравнение результатов расчета тестовой задачи с известным результатом Э.И. Григолюка и Е.А. Лопани-цына позволяет судить о достоверности полученных данных. Математическая модель, алгоритм расчета и методика исследования сферических оболочек на прочность и устойчивость могут быть использованы в организациях, занимающихся проектированием большепролетных строительных сооружений, в научных исследованиях и учебном процессе.

Выявлено, что для рассматриваемой конструкции потеря прочности наступает значительно раньше потери устойчивости, в связи с чем может быть рекомендовано для ее проектирования выбрать марку стали с более высоким значением предела текучести. Шарнирно-неподвижное закрепление в данном случае дает более высокое значение предельно допустимой нагрузки.

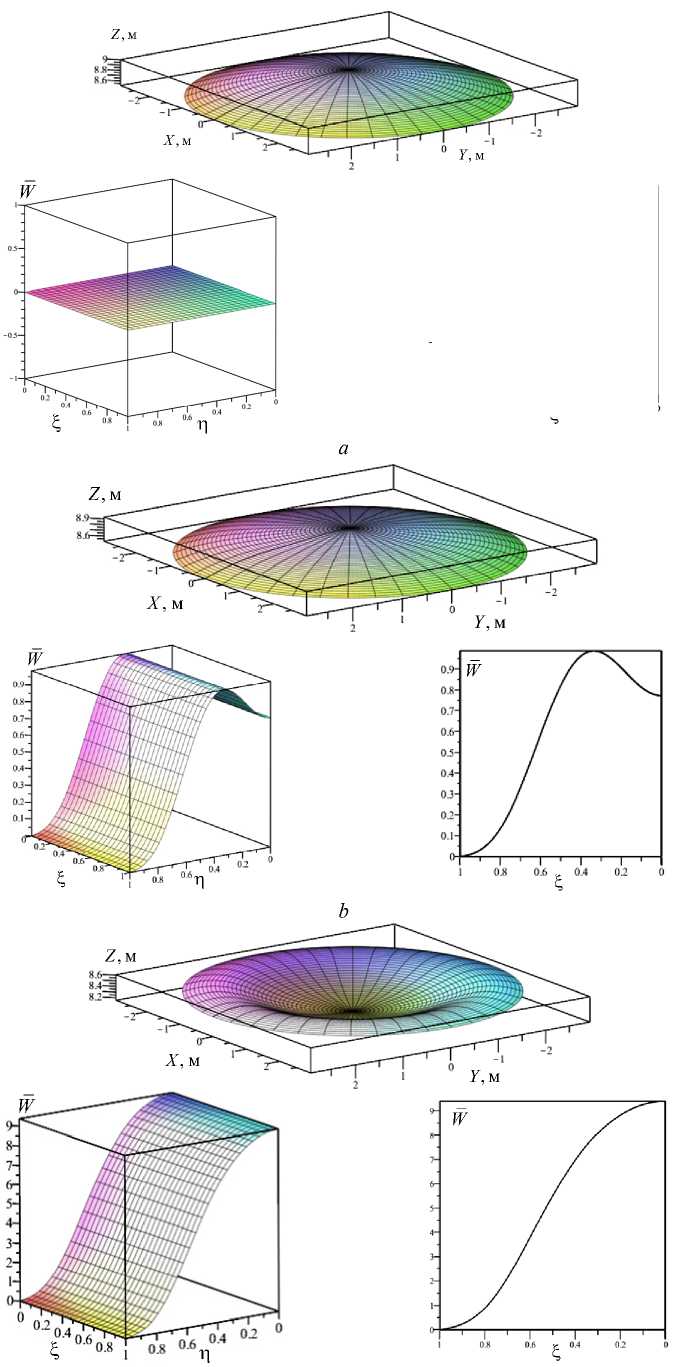
c

Рис. 5. Сферическая оболочка в недеформированном ( a ), докритическом (при нагрузке 0,896 МПа) ( b ) и в закритическом состояниях (при нагрузке 0,896 МПа) ( с )

Fig. 5. Spherical shell in undeformed ( a ), subcritical (at a load of 0.896 MPa) ( b ) and in supercritical states (at a load of 0.896 MPa) ( c )

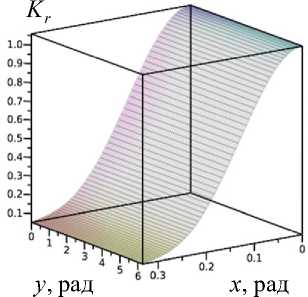
N = 4, q pr = 2,27 Мпа

y , рад              х , рад

N = 9, q pr = 3,39 МПа

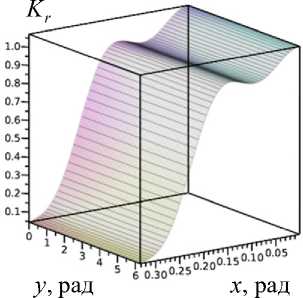
N = 16, q pr = 3,38 МПа

Рис. 6. Поле критерия Мизеса при разных значениях N при достижении предельно допустимой нагрузки

Fig. 6. Von Mises criterion at different values of N when the maximum allowable load is reached