Методика расчета температуры обмоток электрической машины на основе количественной термографии

В процессе конструирования электрических аппаратов решаются прямые и обратные задачи теплового расчета . Первая прямая задача – определение допустимой нагрузки аппарата с учетом предельной температуры, геометрии, способа охлаждения и значения коэффициента теплоотдачи. Первая обратная задача – определение величины требуемой охлаждающей поверхности при известном способе охлаждения, допустимой температуре и нагрузке. Прямые задачи теплового расчета электрических машин разработаны отечественными учеными, в том числе Борисенко А.И., Бурковским А.Н., Гольдбергом О.Д., Гуревичем Э.И., Гуриным Я.С., Ройзеном Л.И., Сипайловым Г.А., Филипповым И.С. и другими.

Вторая прямая задача – установление способа и параметров охлаждения с учетом нагрузки, класса нагревостойкости изоляции обмоток и геометрических особенностей аппарата. Вторая обратная задача, связанная с проведением анализа температурного поля поверхности объекта, расчета температуры внутри объема для определения его технического состояния, практически не анализируется и в литературе не представлена.

С этой позиции тепловизионная диагностика, выступая как метод решения второй обратной задачи, требует развития диагностических моделей исследуемых объектов. Для решения обратной задачи теплового расчета электрических машин актуальным является разработка методики оценки температуры обмотки в пазах статора на основе анализа тепловых потоков от станины. Решение обратной тепловой задачи позволяет рассчитать температуру внутренних частей машины, в том числе температуру обмотки в пазах статора.

В настоящее время тепловизионный контроль, например, двигателей, сводится к выявлению нарушенных контактных соединений в клеммных коробках. По данным тепловизионных испытаний может быть определена температура поверхности обмоток, некоторые части которых, например, лобовых, доступны для тепловизионного анализа ( Власов , 2006a; 2006b).

Тепловизионное обследование обмоток большинства электрических машин, в частности, асинхронных двигателей серии 4A, затруднительно, поскольку отсутствует доступ для сканирования поверхности обмоток статора.

Диагностические модели тепловизионной диагностики отдельных электрических аппаратов и конструкций, необходимые для решения второй обратной задачи, учитывают многообразные процессы: тепловыделения в объеме конструкций; проводниковых и диэлектрических материалов; теплопередачи в материалах; теплоотдачи на границе раздела "объект – воздух" и т.п. ( Власов , 2006a; 2006b).

Нами полагается, что в процессе тепловизионной диагностики можно определить не только распределение температуры на поверхности станины электрической машины, характеризуемое тепловыми потоками, распространяющимися радиально от обмоток в пазах сердечника статора, но и рассчитать параметры теплового потока в процессе количественного анализа. В результате расчета определяются различные агрегированные функции, центральной из которых является величина плотности теплового потока qs, однозначно определяемая диагностическим параметром тепловизионной диагностики – температурой поверхности tп(х, y, r) (Власов, 2006a; 2006b).

Рассмотрим предпосылки для создания тепловой модели электрической машины, на основе которой производится расчет величины тепловых потоков с помощью количественной термографии, регистрирующей анизотропные особенности температурного поля поверхности.

• 2.    Описание эксперимента

Проведены тепловые испытания асинхронного двигателя (АИР 80 А4 У3 IP 54), в процессе которых осуществлялось измерение температуры с помощью термопар, установленных в различных точках конструкции, в том числе непосредственно на участке обмотки, находящейся в торце паза статора. Одновременно в ходе испытаний (с крыльчаткой и без крыльчатки) производилось термографирование ребристой поверхности станины в процессе нагрева машины.

Основные параметры исследуемой машины, необходимые для расчета тепловой модели, приведены в табл. 1.

• С учетом известных геометрических размеров (табл. 1) определяются:

  – внешний диаметр станины:

D = Dн1 + 2δст ;(1)

– высота спинки статора:

hс = [(Dн1 – D1)/2] – h1;(2)

– диаметр сердечника статора по концу паза:

Dп = D – 2hс;(3)

– внешняя площадь поверхности станины:

Sст = 2πDL + 2πD2/4.(4)

Таблица 1. Основные геометрические размеры статора, станины и оребренной поверхности

№№	Параметр	Условные обозначения	Формула	Значение
Геометрические размеры АИР 80 А4 У3 IP 54
1	Высота вала двигателя	H , м	–	0,08
2	Внешняя длина станины	L , м	–	0,158
3	Высота ребра	l , м	–	0,018
4	Толщина ребра	δ , м	–	0,003
5	Длина ребристой стенки на станине	b , м	–	0,12
6	Толщина стенки станины	δ ст , м	–	0,006
7	Расстояние между рёбрами	s , м	–	0,0085
8	Длина сердечника статора	l 1 , м	–	0,078
9	Внешний диаметр сердечника статора	D н1 , м	–	0,132
10	Внутренний диаметр сердечника статора	D 1 , м	–	0,088
11	Высота паза	h 1 , м	–	0,013
12	Внешний диаметр станины	D , м	(1)	0,144
13	Высота спинки статора	h с , м	(2)	0,009
14	Диаметр сердечника по концу паза	D п , м	(3)	0,126
15	Внешняя площадь поверхности станины	S ст , м2	(4)	0,175
Параметры материалов и среды
16	Коэффициент теплопроводности воздуха	λ в , Вт/мК	–	0,03
17	Коэффициент теплопроводности ребра станины	λст , Вт/мК	–	130
18	Коэффициент теплопроводности стали 2013	λс , Вт/мК	–	37
19	Температурный коэффициент электрического сопротивления меди обмотки	TК ρ , 1/Κ	–	0,045
20	Односторонняя толщина изоляции паза	b и , м	–	0,0004
21	Коэффициент теплопроводности изоляции паза	λ и , Вт/мK	–	0,16
22	Ток обмотки статора при испытании	I , A	–	4,2
23	Сопротивление обмотки при 20 °С	r 20 , Ом	–	7,8

Электрофизические параметры используемых материалов известны (табл. 1), в частности, станина выполнена из алюминиевого сплава, сердечник набран из листов электротехнической стали 2013.

На рис. 1 приведены фотография (а) и термограмма (б) нагретого двигателя (испытание в течение 80 минут при наличии крыльчатки). Видно, что ребристая поверхность корпуса двигателя (а) характеризуется анизотропией температурного поля (б) в направлениях осей Х , Y . В частности, анализ распределения температуры на участке поверхности, выделенной прямоугольником KBCE , показывает, что температура поверхности станины изменяется в пределах 39,1-57,4 °С при температуре среды t ₀ = 20,5 °C.

а)                                       б)

Рис. 1. Фотография (а) и термограмма (б) двигателя АИР 80 А4 У3

На термограмме (рис. 1б) и гистограмме (рис. 2а) выделена область LNSOPR , условно

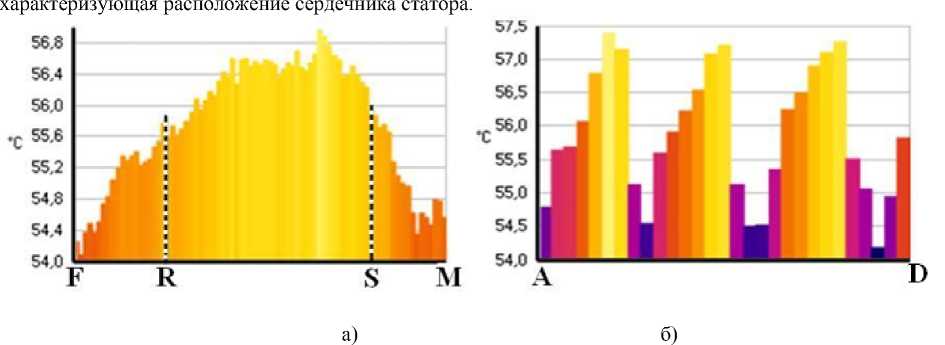
Рис. 2. Гистограммы температур участка FM (а) и участка AD (б) поверхности двигателя

Анализ изменения температуры поверхности (рис. 2) по линейным участкам FM (вдоль ребер по оси Y ) показывает, что наибольшие температуры (до 57 °С) характерны (рис. 2а) для центральной части поверхности станины, непосредственно примыкающей к сердечнику (диапазон между точками RS ). В диапазоне области АD (поперек ребер по оси X ) наибольшие температуры t _макс наблюдаются между ребрами, наименьшие t _мин – на торцах ребер.

• 3.    Описание тепловой модели двигателя

Для анализа теплового состояния машины предложена упрощенная модель, в которую включены: обмотки статора, расположенные в пазах, пленка односторонней изоляции, спинка статора, воздушный зазор между сердечником и ребристой покрышкой, станина (рис. 3).

При расчете тепловой модели (рис. 3) электрической машины учитываются форма, материалы, геометрические размеры: ребра (1) и основания станины (2); воздушного зазора между станиной и спинкой сердечника статора (3); спинки статора (4); пазов с обмоткой (5) и изоляцией (6) в сердечнике статора. В процессе испытаний производится анализ теплового поля поверхности машины с помощью тепловизионной камеры (7). Обработка термограмм с помощью ЭВМ позволяет получить и анализировать гистограммы распределения температурного поля поверхности. Тепловой поток плотностью qs, радиально (по оси r) вытекающий из разогретого сердечника (рис. 1б; рис. 3б, область LNOP), подходит к внутренней несущей стенке станины толщиной δст, и в дальнейшем распространяется в объеме станины в направлении осей +r, ±Y. При оценке величины плотности потока qs следует учитывать возможные пути его распространения. В первом приближении полагается, что тепловой поток распространяется в станине за счет теплопроводности металла и теплоотдачи на поверхности ребра и межреберных промежутков:

• 1)    радиально (по оси r ) через объем несущей стенки и ребро длиной l вплоть до его окончания – поток q_sr (рис. 3а). При радиальном распространении теплового потока от основания ребра к его окончанию температура поверхности ребра t _п( r ) уменьшается от значения t _макс( Y ) до t _мин( Y );

• 2)    продольно (по оси ± Y ) в ребре и несущей стенке станины и, за счет теплопроводности металла от более нагретой центральной части станины (область LNOP ) к торцам станины (рис. 1б; рис. 3б, области KFE и BMC ) – поток q s пр с составляющими q s пр1 и q s пр2 . При продольном распространении потока (вдоль оси ± Y ) температура поверхности уменьшается к торцам, так что температуры t п1 (– L /2) и t п2 (+ L /2) на концах станины меньше, чем в ее центральной части.

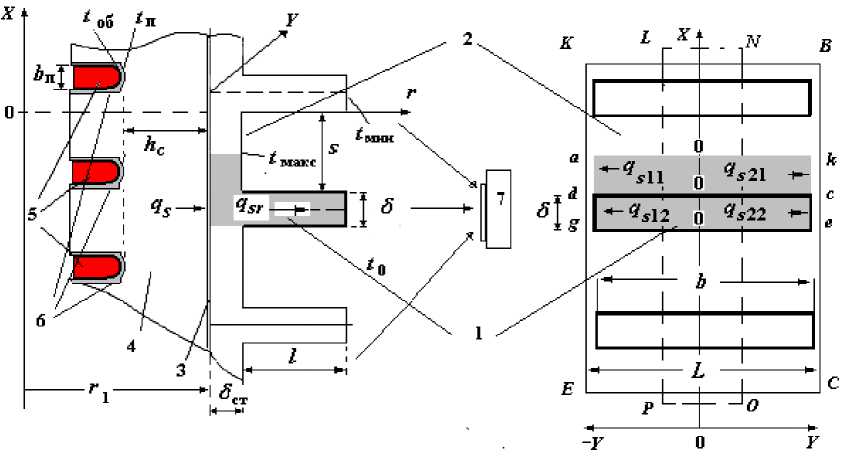
а)                                               б)

Рис. 3. Схематическое изображение сердечника статора, корпуса и ребер станины машины а) вид плоскости Хr ; б) вид плоскости XY

Составляющая теплового потока q s пр1 (по оси – Y ) связана с продольным распространением тепла по объему металла основания станины. Например, для анализа (рис. 3б) выбраны элементы 00 da и 00 dg (толщина δ ст , ширина s /2, длина b /2) – потоки q s пр11 и q s пр12 . Аналогично, составляющая q s пр2 (по оси + Y ), связанная с продольным потоком по объему ребристых элементов 00 kc и 00 ce (толщина δ , ширина l , длина b /2), определяется потоками q s пр21 и q s пр22 (рис. 3б).

В процессе тепловизионных испытаний для каждой точки поверхности оцениваются диагностические параметры: измеренное значение температуры t _п( x , y , r ) и расчетное превышение ϑ ( x , y , r ) температуры:

ϑ ( x , y , r ) = t п ( x , y , r ) – t 0 . (5)

Например, в сечении АD в процессе тепловизионных испытаний выделяется наиболее разогретая область поверхности в центральной области станины, примыкающей к сердечнику. В данной области определяются значения температуры: t 1 = t макс – между ребрами, t l = t мин – на окончании ребра (табл. 2). С учетом соотношения (1) превышения температуры равны:

ϑ осн ⁼ ϑ макс ^{= t} макс ^{– t} 0^; ϑ мин

ϑ l ^{= t} мин ^{– t} 0^; ∆ ^t макс

^t макс

мин.

Распространение теплового потока вдоль произвольного параллелепипеда длиной ∆ Η описывается соотношением ( Исаченко и др. , 1981):

ch( m ∆ Η ) = ϑ осн / ϑ ∆ Η ,

где ϑ ∆ Η , ϑ осн – превышения температуры (по отношению к температуре окружающей среды t 0 ) на конце теплопроводящего элемента и в его основании; коэффициент m равен:

m = ( α u / λ f )^0,5,                                                (8)

где u , f – периметр и площадь сечения исследуемого элемента.

Известно ( Исаченко и др. , 1981), что количество тепла Q , отдаваемого поверхностью элемента в окружающую среду, равное количеству теплоты, подводимого к основанию элемента, определяется соотношением:

Q = ϑ1(αλuf)0,5th(m∆Η),(9)

и, соответственно, плотность теплового потока q s , проходящего через основание элемента, равна:

qs = Q/f = ϑ1(αλu/f)0,5th(m∆Η).(10)

При ограниченной длине ∆ Η элемента для учета теплоотдачи с торца ребра рассчитывается высота ∆ Η ' :

∆Η ' = ∆Η + δ/2.(11)

Площадь f и периметр u поперечного сечения элемента равны:

f = δb;(12)

u = 2(b + δ).(13)

На основе выражения (7) можно рассчитать значение φ , равное:

φ = arccosh(ml).(14)

Расчёт экспериментального значения коэффициента теплоотдачи α производится по выражению α = λf(φ/l)2/u.(15)

• 4.    Расчет коэффициента теплоотдачи с поверхности станины

  При оценке величины теплового потока на основе данных количественной термографии центральной задачей является расчет коэффициента теплоотдачи с поверхности станины электрической машины в произвольных точках поверхности. В работах ( Власов , 2006a; 2006b) обоснована возможность оценки плотности теплового потока по результатам тепловизионной диагностики.

Рассмотрим алгоритм решения этой задачи на основе анализа значений температуры в основании (между ребрами) и на конце ребра (табл. 2).

При радиальном распространении тепла (рис. 3а) через ребро прямоугольной формы коэффициент m r рассчитывается по соотношению (8):

m r = ( α r u р / λ ст f р )^0,5.                                          (16)

Несмотря на то, что температура поверхности ребра при радиальном тепловом потоке уменьшается от основания к его окончанию, в первом приближении принимается, что коэффициент теплоотдачи α r различных точек поверхности ребра (при фиксированном Y ) одинаков. В то же время, полагается, что коэффициент α пр изменяется по мере удаления от центра станины к ее торцам (по оси Y ) из-за значительной анизотропии температурного поля.

На основе термографического обследования определяются температуры и производится расчет экспериментального значения отношения ϑ _мaкс/ ϑ _мин, и при известных характеристиках ребра станины (табл. 2) по соотношениям (8-16) рассчитывается экспериментальное значение величины m r эксп :

где l ' = l + δ /2.

mr эксп = [arcch(ϑмакс/ϑмин)]/l', на поверхности ребер в

Экспериментальное значение коэффициента теплоотдачи α r эксп исследуемой области поверхности рассчитывается по соотношению:

α r эксп ⁼ m r эксп λ ст f р / u р^.

Таким образом, можно рассчитать локальные значения коэффициентов теплоотдачи α _i в различных точках поверхности: α _ц – в наиболее разогретой центральной области (сечение AD ) станины, α _{т i} – на левом и правом торцах станины ( α _тл – в области KFE , α _тпр – в области BMC ), интегральные и средние значения α i , определяющие теплоотдачу со всей поверхности станины. Например, среднее значение коэффициента теплоотдачи от поверхности с учетом изменения теплоотдачи по координате Y :

α ср = ( α ц + α т i )/2.

• 5.    Расчет плотности теплового потока

С учетом положений, рассмотренных выше в п. 3, полагается, что суммарная плотность q s теплового потока, подходящего к поверхности из нагретого сердечника, определяется соотношением:

q _s = q_sr + q_{s пр} = q_sr + Σ q_si k = q_{s r} + q_{s 1} + q_{s 2};

q s 1 = q s 11 + q s 12 ;                                                     (20)

q s 2 = q s 21 + q s 22 .

Поверхностная плотность теплового потока q s рассчитывается на основе экспериментальных данных количественной термографии поверхности машины.

Рассмотрим алгоритм расчета плотности теплового потока q_s в области поверхности с максимальной температурой t мах , определяемой в процессе тепловизионных испытаний.

Величина плотности qsr теплового потока, входящего в ребро станины и распространяющегося радиально по оси r, определяется выражением, представленным в работе (Ройзен, Дулькин, 1977) при решении уравнения теплопроводности:

qs = αϑ1/k,(21)

где k = (Biр + Bic1/2thNcт)/(Biр1/2thN + Bic1/2thNcт);(22)

коэффициенты Био определяются:

Вiр = αδ/2λст; Вiст = αδcт/2λст;(23)

характеристические размеры равны:

Nр = l(2αц/λстδр)1/2, Ncт = (s/2)(α ц/λстδcт)1/2.(24)

Значения коэффициентов m р , характеристический параметр ребра N р , число Био рeбра и Bi р взаимосвязаны:

mр= [αцu/(λтf)]2;(25)

Nр = mрl'.(26)

С учетом известных геометрических значений параметров ребра и станины рассчитываются коэффициенты Био и характеристические размеры (табл. 2).

При расчете величины плотности q_{s пр i} теплового потока, распространяющегося продольно в направлении ± Y , принимается, что теплопроводность осуществляется в теплопроводящих элементах постоянного поперечного сечения: в ребре станины и промежутке между ребрами (элементы akcd и dceg , выделенные на рис. 3б).

Характеристические размеры и коэффициенты, определяющие тепловые потоки q_sik через выделенные теплопроводящие элементы (левый торец: 00 da , 00 dg ; правый торец: 00 kc , 00 ce ), рассчитываются с учетом строения основания и ребра станины.

Для элементов 00 da и 00 dg (потоки q s 11 и q s 12 ), 00 kc и 00 ce (потоки q s 21 и q s 22 ) имеем:

– периметры:

П11 = П21 = 2(s/2 + δст), П12 = П22 = 2∙(l + δ + δст);(27)

– площади сечения элемента:

А11 = А21 = δстs/2, А12 = А22 = (l + δст)δ;(28)

– коэффициенты m 11 и m 21 , m 12 и m 22 :

m11 = (2αср лП11/λстs) , ; m12 = (αср лП12/(λстА12)) , ;(29)

m21 = (2αср пП12/λстs) , ; m22 = (αср пП12/(λстА22)) , .(30)

При соответствующей избыточной температуре ϑ _i (превышение температуры на концах выделенного элемента) между областью горячей точки и торцом станины, значения плотности теплового потока q s ik в сечении 00 определяются соотношением, аналогичным (10):

qsik = ϑi(αср iλстПik/Аik)0,5th(mikL/2),(31)

где α ср i – среднее значение коэффициента теплоотдачи на поверхности элемента; П ik , А ik , m ik – параметры элемента, характеризующие поверхность станины, прилегающую к ее торцам; L /2 – примерная длина элемента. Расчетные значения тепловых потоков приведены в табл. 2.

Таблица 2. Пример расчета на основе данных количественной термографии

№	Параметр	Формула	Значение
24	Температура окружающей среды t 0 , оС	–	20,5
Расчет коэффициента теплоотдачи α ц и m ц в центральной части станины
25	Максимальная температура между рёбрами t 1 = t мaкс , оС	–	57,4
26	Максимальная температура на конце ребра tl = t мин , оС	–	54,4
27	Превышение температуры в основании ребра ϑ 1 = ϑ макс , оС	(6)	36,9
28	Превышение температуры на конце ребра ϑ l = ϑ мин , оС	(6)	33,9
29	l ', м	(11), (17)	0,02
30	f р , м2	(12)	0,00036
31	u р , м	(13)	0,246
32	Отношение ch( m ∆ Η ) = ϑ 1 / θ l | макс	(7)	1,088
33	Значение φ , рад	(14)	0,418
34	Значение коэффициента теплоотдачи α ц , Вт/м2оС	(15), (18)	87,3
35	Значение m ц в центральной части станины	(16), (17)	21,42

Расчет коэффициента теплоотдачи α л в области левого торца станины ( точка F )
36	Температура между рёбрами t 1л , оС	–	46,7
37	Температура на конце ребра t l л , оС	–	43
38	Превышение температуры в основании ребра ϑ 1л , оС	(6)	26,2
39	Превышение температуры на конце ребра ϑ l л , оС	(6)	22,5
40	Отношение ch( m ∆ Η ) = ϑ 1 / θ l | л	(7)	1,164
41	Значение φ л , рад	(14)	0,566
42	Значение коэффициента теплоотдачи α л , Вт/м2оС	(15), (18)	160,3
43	Среднее значение коэффициента теплоотдачи в левой части поверхности станины α ср л , Вт/м2 оС	(19)	123,8
Расчет коэффициента теплоотдачи α п и m п в области правого торца станины ( точка М )
44	Температура между рёбрами t 1п , оС	–	55,5
45	Температура на конце ребра t l п , оС	–	53,8
46	Превышение температуры в основании ребра ϑ 1п , оС	(6)	35
47	Превышение температуры на конце ребра ϑ l п , оС	(6)	33,3
48	Отношение ch( m ∆ Η ) = ϑ 1 / θ l | п	(7)	1,051
49	Значение φ п , рад	(14)	0,318
50	Значение коэффициента теплоотдачи α п, Вт/м2оС	(15), (18)	50,66
51	Среднее значение коэффициента теплоотдачи в левой части поверхности станины α ср п, Вт/м2оС	(19)	68,97
Расчет плотности радиального теплового потока qsr
Расчет коэффициентов Био и характеристические размеры станины и ребра
52	Коэффициенты Био Вi ст	(23)	0,004
53	Характеристический параметр стенки станины N ст	(24)	0,045
54	Значение m р	(25)	21,42
55	Характеристический параметр N р ребра	(26)	0,418
56	Коэффициенты Био Вi р	(23)	0,001
57	Коэффициент k	(22)	0,251
58	Плотность радиально распространяющегося теплового потока qsr , Вт/м2	(21)	12841
Расчет характеристических размеров элементов при продольном потоке
59	Периметр элементов П 11 = П 21 , м	(27)	0,021
60	Периметр элемента П 12 = П 22 , м	(27)	0,054
61	Площадь сечения элемента A 11 = A 21 , м2	(28)	0,000026
62	Площадь сечения элемента A 12 = A 22 , м2	(28)	0,000072
	Расчет коэффициентов mik
63	Значение m 11	(29)	2,143
64	Значение m 12	(29)	26,72
65	Значение m 21	(30)	1,6
66	Значение m 22	(30)	19,947
Расчет плотностей продольного теплового потока qs 11 и qs 12 ( рис. 3б )
67	Температура торца t ′ , оС в области dg	–	43
68	Плотность теплового потока qs 11 , Вт/м2	(31)	6452,5
69	Плотность теплового потока qs 12 , Вт/м2	(31)	36744
70	Суммарное значение qs 1	(20)	43197
Расчет плотностей продольного теплового потока qs 21 и qs 22 ( рис. 3б )
71	Температура торца t ′′ т , oC	–	53,8
72	Плотность теплового потока qs 22 , Вт/м2	(31)	642
73	Плотность теплового потока qs 21 , Вт/м2	(31)	1310
74	Суммарное значение qs 2 , Вт/м2	(20)	1951
75	Суммарное значение q s , Вт/м2	(20)	57989

• 6.    Расчет температуры поверхности обмотки

  Температура обмотки, расположенной в пазу статора, рассчитывается по методу термических сопротивлений. Подобная методика применяется в расчетах при решении прямой задачи при известных значениях параметров исследуемой машины и величины теплового потока, проходящего через слои конструкции: основание станины, воздушный зазор, спинку статора h _c, изоляцию паза с толщинами δ _ст, h _c, δ _з, b ₁, соответственно ( Борисенко и др. , 1983; Бурковский и др ., 1970; Сипайлов и др. , 1989; Радин и др. , 1990; Гурин, Кузнецов , 1978).

Поскольку величина плотности q s в различных сечениях конструкции цилиндрической формы определяется радиусом r , нами произведен учет значения линейной плотности q L теплового потока, не зависимого от величины r и определяемого соотношением:

q L = п D н1 q s = 2 п r н1 q s ,

где D _н1 и r _н1 - внешний диаметр и радиус сердечника статора.

Полагается, что тепловой поток плотностью q_L проходит через спинку статора, воздушный зазор, основание станины, так что при распространении тепла через элементы конструкции выполняются следующие соотношения:

q L = пА t ст / R l ст = пА t з / R l з = пА t _п/ R l с ;

• ^qL м    ^пА t из / R L из ;

^А t ст = ⁽ t з ^_ t макс^{); А} t з = ⁽ t ст ^_ t з^{); А} t с = ⁽ t из ^- t ст^{); А} t из = ⁽ t об ^- t из )»

где t _з, t _ст, t _из, t об — температуры на внутренней поверхности основания станины, внешней поверхности сердечника статора, поверхности изоляции паза, обмотке (под изоляцией паза); А t _ст, А t _з, А t _с, А t _из -превышения температуры на основании станины, воздушном зазоре, спинке сердечника статора, односторонней изоляции паза; R L _ст, R L _з, R L _с, R L _из - линейные термические сопротивления отдельных слоев конструкции (табл. 2):

основания станины: R L _ст = (1/2 Л _ст)1п[( D _н1 + 2 5 _з + 2 5 _ст)/( D _н1 + 2 S _;)];

воздушного зазора: R L _з = (1/2 Л в )1п[( D _н1 + 2 5 _з)/ D _н1];                                              (36)

спинки сердечника статора: R L _с = (1/2 Л _с)1п[ D _н1/( D _н1 - 2 h _с)];

односторонней пазовой изоляции: R L _из = (1/2 Л и )1п[ D _п/( D _п - 2 b _и)].

Величина линейного теплового сопротивления R L _из изоляции паза учитывает значение b _и -одностороннюю толщину изоляции в пазу статора, Л и - эквивалентную теплопроводность пазовой изоляции обмотки, D _п - диаметр сердечника статора по концу паза.

Продолжение таблицы 2

Расчетные значения термических сопротивлений и превышения температуры на слоях
76	Линейная плотность теплового потока, qL , Вт/м	(32)	24054
77	Линейное тепловое сопротивление станины R L ст , моС/Вт	(36)	3,347^10 " 4
78	Линейное тепловое сопротивление зазора R L з , моС/Вт	(36)	= 0
79	Линейное тепловое сопротивление спинки статора R L с , моС/Вт	(36)	19,3^10 " 4
80	Линейное термическое сопротивление односторонней пазовой изоляции R L из , моС/Вт	(36)	0,02
81	Количество пазов, Z	–	36
82	Шаг обмотки, у	(37)	9
83	Число пар полюсов, p		2
84	Среднее зубцовое деление статора, t ср , мм	(38)	8,85
85	Средняя ширина катушки обмотки статора, b ср , мм	(39)	79,63
86	Средняя длина одной лобовой части катушки L л1 , мм	(40)	118,52
87	Средняя длина витка обмотки 1 1 ', мм	(41)	0,1963
88	Сопротивление обмотки в нагретом состоянии R , Ом	(43)	8,7
89	Электрические потери в обмотке статора при нагрузке, Р м , Вт	(43)	461,5
90	Линейная плотность теплового потока обмотки qL м , Вт/м	(44)	2349,84
Расчетные и экспериментальные значения температуры
91	Превышение температуры в стенке станины А t ст , оС	(35)	2,56
92	Превышение температуры в воздушном зазоре А t з , оС	(35)	= 0
93	Превышение температуры в спинке статора А t с , оС	(35)	14,8
94	Превышение температуры на пазовой изоляции А t из , оС	(35)	14,85
95	Расчетное значение температуры поверхности обмотки t расч , оС	(46)	89,6
96	Экспериментальное значение температуры поверхности обмотки t эксп , оС		92,1

Полагается, что через одностороннюю изоляцию паза, примыкающую к обмотке, проходит, в основном, поток, обусловленный джоулевскими потерями в нагретой обмотке паза. Оценка линейной плотности данного потока производится следующим образом. Считается, что тепловой поток Р _м от обмотки, обусловленный протекающим током, распределяется по средней длине 1 1 одного проводника. Значение 1 1 ' определяется с учетом известных конструкционных данных (табл. 1) по методике, аналогичной описанной в литературе ( Гурин, Кузнецов , 1978), согласно которой рассчитываются значения:

• -    шага обмотки у при известном значении количества пазов Z и числа пар полюсов р :

у = Z /2 p ;                                                   (37)

• -    среднего зубцового деления t _ср статора:

tср = 103∙(π(D1 + h1)/Z);(38)

• –    средней ширины катушки обмотки статора:

bср = tсрy;(39)

• –    средней длины L _л1 одной лобовой части катушки:

Lл1 = (1,16 + 0,14)bср + 15;(40)

• –    средней длины l 1 ' витка обмотки:

l1' = (l1+ Lл1)/103.(41)

С учетом известных значений тока I можно оценить электрические потери при нагрузке, в частности: – сопротивление R ( ϑ ) нагретой обмотки при повышенной температуре:

R(ϑ) = r20∙(1 + TКρ∙ϑ′1),(42)

где r ₂₀ – сопротивление обмотки при 20 °С; ϑ ′ ₁ – превышение температуры обмотки в горячем состоянии по отношению к температуре 20 °С;

• –    электрические потери P _м1 в обмотке статора при нагрузке:

Pм1 = 3R(ϑ)I2.(43)

Окончательно, линейная плотность q L м теплового потока обмотки равна:

qLм = Pм1/l1'.(44)

Параметры конструкции исследуемой электрической машины известны (табл. 1). Величина воздушного зазора δ _з определяется различными соотношениями, в частности ( Сипайлов и др. , 1989):

δз = (0,42 + 3,16Dн1)∙10-5 м.(45)

Величина воздушного зазора, рассчитанная с учетом соотношения (45), может достигать 8 мкм. Расчеты показывают, что в диапазоне температур до 100 °С превышение температуры ∆ t з на воздушном зазоре не превышает 1-2 °С, поэтому в первом приближении влиянием зазора можно пренебречь. Это связано с несколькими факторами:

• –    анализ анизотропии теплового поля на поверхности машины позволяет предположить, что именно в области наиболее горячей точки поверхности станины осуществляется наиболее плотный "механический" контакт между сердечником и станиной, так что воздушный зазор в этой области пренебрежимо мал;

• –    при анализе влияния тонкого (размером 8-16 мкм) воздушного зазора следует учитывать, что значение коэффициента теплопроводности воздуха λ _в может превышать табличное значение ( λ _табл ≈ 0,03 Вт/мК) в 4-10 раз, так что теплопередача через потенциально возможную прослойку увеличивается.

• 7. Заключение

На основании расчетных значений R_{L ст}, R_{L з}, R_{L с}, R _из и величины линейной плотности теплового потока q L , q L м из соотношения (35) можно рассчитать превышение температуры ∆ t i в каждом анализируемом слое конструкции (табл. 2) и, в конечном счете, определить значение температуры поверхности обмотки t об , расположенной в пазу статора:

t об = t макс + ∆ t ст + ∆ t з + ∆ t с + ∆ t из .                                  (46)

В частности, в установившемся режиме работы двигателя значение температуры обмотки, экспериментально измеренное с помощью термопары, достигает значения t _эксп ≈ 92,1 °С, расчетное значение t расч достигает величины 89,6 °С (без воздушного зазора).

На рис. 4 приведены экспериментальные данные температуры t мин (кривая 4), t макс (кривая 3), определяемые при термографическом испытании, как значения температуры в наиболее нагретой центральной области станины, температуры t об эксп обмотки (кривая 1) в пазу статора, измеренные термопарой, а также расчетные данные температуры t об расч (кривая 2), полученные на основе обработки данных тепловизионных испытаний (с крыльчаткой) по методике, описанной выше.

Анализ показывает, что при анализируемых параметрах расчетные данные с погрешностью ± 5 % адекватно описывают экспериментальные значения температуры обмотки в пазу статора, измеренные с помощью термопары.

Видно, что при достижении равновесного термического состояния температура обмоток достигает 92 °С, превышая максимальную температуру станины на 30-35 °С.

Проведенный теоретический и экспериментальный анализ теплового состояния реального электрического двигателя показывает, что техническая диагностика на основе количественной термографии с достаточной степенью точности позволяет произвести расчет температуры в объеме обмотки при различных нагрузках. Расчетные данные с относительной погрешностью ± 5 % адекватно описывают экспериментальные значения температуры обмотки в пазу статора, измеренные с помощью термопары.

При небольших временах испытаний (до 10-15 минут) наблюдается повышенная погрешность расчетных значений, что связано с нерегулярным процессом нагрева машины.

Дальнейшее развитие тепловой модели должно быть связано с учетом влияния нагрева ротора, анализом анизотропии распределения температуры по длине обмотки и на ее торцах, оценкой превышения температуры в объеме пазовой обмотки.

Достоинством разработанной методики оценки теплового состояния электродвигателей на основе количественной термографии является визуальная локализация местоположения мест перегрева обмотки, обусловленных особенностями распространения тепла, дистанционная оценка наибольших значений температуры обмоток статора в процессе эксплуатации.

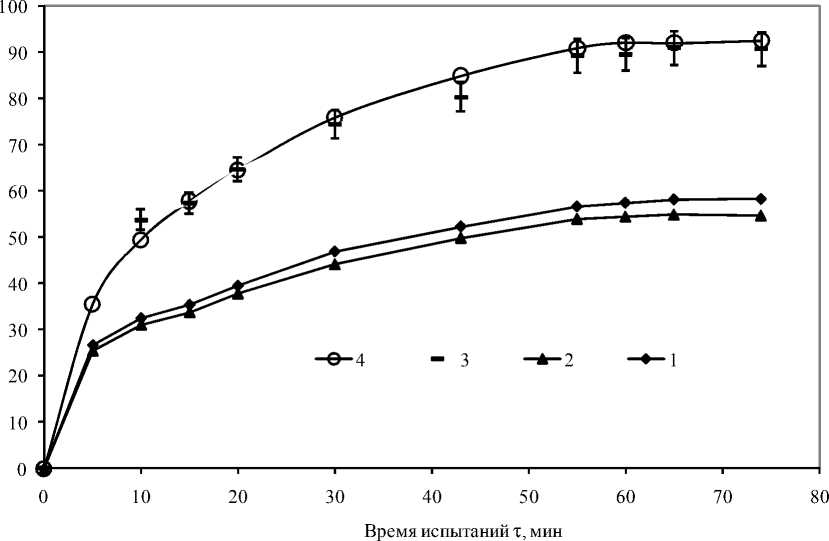
Рис. 4. Изменение температуры от времени испытаний:

1 – t _о б _эксп; 2 – t _о б _.расч; 3 – t _макс; 4 – t _мин