Методика расчета угла бросания удобрений и семян центробежным аппаратом с отклоненными от радиуса лопатками как функции случайных координат точки подачи

Введение. В сельскохозяйственном производстве достаточно широкое применение получили разбрасыватели (или рассеиватели) удобрений, которые применяются не только для распределения по поверхности поля основных доз, собственно, самих удобрений, но и семян отдельных культур, которые могут высеваться разбросным способом, таких, например, как ячмень, рис, травы, бобовые и др. [1, 2].

В подавляющем большинстве случаев на практике используют центробежные разбрасыватели для рассева минеральных удобрений и семян, поскольку они просты по конструкции, производительны, удобны в загрузке, поэтому получили большое распространение. Теория функционирования центробежных аппаратов получила значительное развитие [3–5, 13, 14], в том числе и в области дифференцированной подачи распределяемых материалов [6–9,

15, 16]. Однако в теории рассматривается движение одиночных частиц, что ограничивает применение таких зависимостей в конструкторских расчетах. Струя удобрений или семян, подаваемых на распределяющий аппарат, под действием удара лопатками получает разброс по углу и по радиусу подачи [10], поэтому программы вычисления угла бросания необходимо усовершенствовать так, чтобы угол бросания определялся как функция двух случайных аргументов – полярных координат точек подачи.

Целью представленного исследования является разработка методики расчета распределения угла бросания частиц как функции двух случайных элементов и программы для её реализации. Достижение этой цели позволит повысить адекватность дальнейших расчетов равномерности распределения удобрений и семян по поверхности поля.

Методика исследования.

Проводилось аналитическое исследование характеристик угла бросания [11, 12] с помощью пакета программ Mathcad. Пакет состоит из четырех программ.

При разработке методики расчета исходили из того, что угол бросания α (рисунок 1) относительно линии движения может быть определен исходя из зависимости

α = λ + ω ⋅ t ₁ + φ ₀ + φ _R + θ - π , (1) где λ – угловая координата точки подачи частицы;

ω t ₁ – угол схода частицы, т.е. угловое перемещение частицы в абсолютном движении до момента схода с лопатки;

φ ₀ – угол отклонения лопатки от радиального положения в точке подачи;

φ _R – угол отклонения лопатки от радиуса в точке схода частицы с лопатки;

θ – угол между вектором абсолютной

скорости и радиус-вектором частицы.

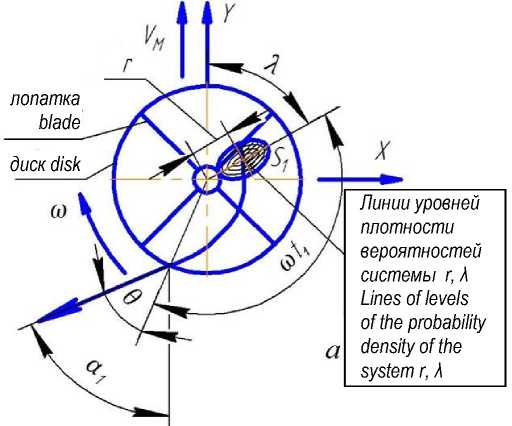
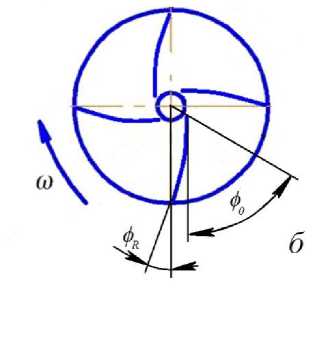
а – схема движения материала при взаимодействии с радиальными лопатками (частный случай); б – основные угловые параметры лопаток при их арадиальном расположении

Рисунок 1 – Схема к определению кинематических параметров частицы при сходе с лопатки a – scheme of material movement during interaction with radial blades (special case);

b – the main angular parameters of the blades with their radial arrangement

Figure 1 – Scheme for determining the kinematic parameters of the particle when leaving the blade

Угол схода частицы ωt l находится умножением угловой скорости диска на время движения частицы по лопатке, которое находится совместным решением уравнения движения частицы по лопатке и конечной длины лопатки. Угол схода частиц с диска ωt l является функцией радиуса подачи r и угловой координаты точки подачи.

Углы а , X отсчитываются от продольной оси координат в направлении вращения диска.

Заданное постоянное значение угла бросания α можно получить только при определенных сочетаниях аргументов. Для диска с радиальными лопатками заданное значение угла бросания получается при подаче частиц на линии равных углов бросания. В полярных координатах r, λ это логарифмическая спираль [10] вида ρ = а·ехр (кλ), где а и к – параметры спирали, определяемые по зависимостям:

а = ———ехр( — ^{1 51Л} * (а — 0)); (2)

• 1    + SІTlф ^V COS ф ^V 77 \ /

к = ctg-д = (3) ^a COSф ' '

Подача удобрений или семян в любую точку спирали дает заданное постоянное значение угла α. Форма спирали зависит только от угла трения частиц по лопаткам, а ее расположение – от φ, α и R. Линия равных углов бросания существует и для диска с отклоненными от радиуса лопатками, но её построение необходимо выполнять с помощью специальной программы.

Спираль, построенная при α = α 1 , делит зону подачи удобрений на две части (рисунок 1 а ) [10]. Сочетания r, λ , принадлежащие площади S 1 , расположенной правее спирали, обеспечивают получение угла α меньше α 1 , а при r, λ, не принадлежащих площади S 1 , имеем α > α 1 .

Функция распределения случайной величины α может быть получена интегрированием плотности системы r, λ по площади S 1 .

Результаты исследования и их обсуждение. Покажем применение методики расчета угла бросания для аппарата с отклоненными от радиуса лопатками (рисунок 1 б ). При этом, при проведении расчетов в демонстративных целях зададимся абстрактными значениями статистических характеристик входных параметров.

Алгоритм расчета.

• 1.    Записать исходные данные: математическое ожидание радиуса подачи Mr ; среднее квадратическое отклонение радиуса подачи σ r ; математическое ожидание угловой координаты точки подачи удобрений M λ ; среднее квадратическое отклонение угловой координаты подачи σλ ; радиус распределяющего диска R ; угол наклона лопатки к радиусу ψ ; коэффициент трения удобрений по материалу лопатки f ; угловая скорость диска ω .

• 2.    Создать векторы r i ; X j с числом элементов Nr = N X = 12 . Тогда интервалы между элементами векторов равны: 0,5 -o r ;0.5 - oX .

• 3.    Создать матрицу Mf плотности вероятностей двухмерного распределения координат подачи r i ; X j . Случайные величины считаем независимыми, поэтому плотность вероятности для всех сочетаний r ; X j определяем по программе Mf для двухмерного нормального распределения (рисунок 2).

r i = i - 0,5 - o r + Mr - 3 - o r ; (4)

Xj = j - 0,5-oX+MX-3-oX. (5)

Полученный при решении программы Mf массив результатов может быть выражен графически, в виде поверхности рисунок 3), или в виде матрицы. отклика (для рассматриваемого случая –

Mf := Mr <-0.14

err <-0.01

MX <-0.8

crX <- 0.4

NX <- 12

lor j e 0.. NX

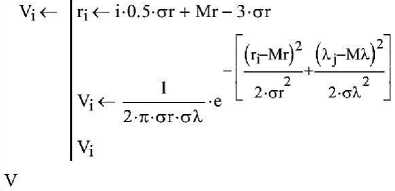
Рисунок 2 – Программа расчета плотностей вероятностей координат подачи частиц рассеваемого материала

м Д < ■ V

Mfi,j

Mf

Figure 2 – The program for calculating the probability densities of the coordinates of the supply of particles of the sieved material

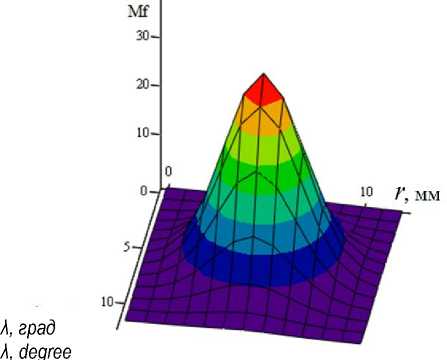
Рисунок 3 – Матрица плотностей вероятностей координат подачи Figure 3 – The probability density matrix of feed coordinates

4. Создать матрицу  Mα  углов бросания для всех сочетаний ri ; λj .

Программа Mα (рисунок 4) имеет два цикла, в которых изменяет полярные

координаты точек подачи удобрений и вычисляет угол бросания диском с отклоненными от радиуса лопатками как функцию полярных координат точек подачи

[11, 12]. При этом матрица результатов Mf данных, используемых при реализации является, по сути, массивом исходных

Ma :=

Mr 4- 0.14

программы M α (рисунок 4).

at 4- 0.01

MX •«-0.6

ok 4- 0.4

yR — 03

to 4- 100

NX 4- 12

Ma(j^

Nt 4- 12

Vj 4-

r, 4— i0.5ar + Mr - 3-ar

Vj 4—

f 4- 0.6

4> 4- atan(f)

R 4- 0.3

to 4- 10O

64-9.R

2 to

4» 4- atan(f)

XI 4— -fto +

2     2

+■ to

X2 <- -f to

2      2

+■ to

со$(уо + ф)

' СОі(ф)

£R 4— R'COS(_VR)- rj'Ml(^o)

14-0 01

X2

X2 - Xi

•exp(xi-t) -

XI

X2 -XI

exp(x2-t) - 1 - l^R ,t

XI .X2-(B - A)

Vr4---------

X2 - X]

Ө 4- alan

to'R

Vr

Alj 4— X j + to '11 + tyo — ty R + Ө — it

Vj 4— Al;

Vj

Vj

V

Ma^ 4- V

Ма;;

Ma

Рисунок 4 – Программа расчета угла бросания удобрений центробежным аппаратом как функция двух аргументов: угла и радиуса подачи

Figure 4 – The program for calculating the angle of throwing fertilizers by a centrifugal apparatus as a function of two arguments: the angle and radius of the feed

Результат счета также может выводиться в виде матрицы (рисунок 5) или поверхности отклика.

	-0.191	9.213 x 10" 3	0.209	0.409	0.609	0.809	1.009	1.209	1.409	1.609	1.809	2.009	2.209
	-0.274	-0.074	0.126	0.326	0.526	0.726	0.926	1.126	1.326	1.526	1.726	1.926	2.126
	-0.354	-0.154	0.046	0.246	0.446	0.646	0.846	1.046	1.246	1.446	1.646	1.846	2.046
	-0.431	-0.231	-0.031	0.169	0.369	0.569	0.769	0.969	1.169	1.369	1.569	1.769	1.969
	-0.505	-0.305	-0.105	0.095	0.295	0.495	0.695	0.895	1.095	1.295	1.495	1.695	1.895
	-0.576	-0.376	-0.176	0.024	0.224	0.424	0.624	0.824	1.024	1.224	1.424	1.624	1.824
Ma =	-0.645	-0.445	-0.245	-0.045	0.155	0.355	0.555	0.755	0.955	1.155	1.355	1.555	1.755
	-0.711	-0.511	-0.311	-0.111	0.089	0.289	0.489	0.689	0.889	1.089	1.289	1.489	1.689
	-0.776	-0.576	-0.376	-0.176	0.024	0.224	0.424	0.624	0.824	1.024	1.224	1.424	1.624
	-0.838	-0.638	-0.438	-0.238	-0.038	0.162	0.362	0.562	0.762	0.962	1.162	1.362	1.562
	-0.899	-0.699	-0.499	-0.299	-0.099	0.101	0.301	0.501	0.701	0.901	1.101	1.301	1.501
	-0.958	-0.758	-0.558	-0.358	-0.158	0.042	0.242	0.442	0.642	0.842	1.042	1.242	1.442
	^-1.016	-0.816	-0.616	-0.416	-0.216	-0.016	0.184	0.384	0.584	0.784	0.984	1.184	1.384

Рисунок 5 – Вывод результата счета программой Mα

• Figure 5    – Output of the result of the calculation by the program Mα

  По матрице M α можно определить математическое ожидание угла бросания. Для двухдискового аппарата необходимо получить M α = 0,6 рад, для однодискового – M α = 0. Такие значения необходимо получить в центре матрицы (поверхности). Корректировать их можно изменением M λ .

  5. Выделить из матрицы Mf элементы, соответствующие получению угла бросания,

  
  

  меньше заданного числом А. Суммированием выделенных элементов матрицы и умножением суммы на интервалы изменения векторов r i , X j получаем значение функции распределения угла бросания.

  Выделение элементов матрицы Mf выполняет программа Ms(A) (рисунок 6).

  
  

Ms(A) :=

NX <- 12

for j e 0.. NX

Ms^

NX <- 12

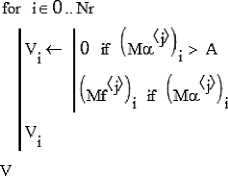
Рисунок 6 – Программа выделения элементов матрицы Mf по условию M α < A

• Figure 6    – Matrix element selection program Mf by condition M α < A

Ms^

Ms

Результат расчета матрицы Ms при А = 0,4 представлен на рисунке 7.

	(         - з 4.91x10	0.019	0.06	0	0	0	0	0	0	0	0	0	0
	0.019	0.077	0.237	0.568	0	0	0	0	0	0	0	0	0
	0.06	0.237	0.729	1.748	0	0	0	0	0	0	0	0	0
	0.144	0.568	1.748	4.194	7.835	0	0	0	0	0	0	0	0
	0.268	1.06	3.266	7.835	14.637	0	0	0	0	0	0	0	0
	0.39	1.543	4.752	11.4	21.297	0	0	0	0	0	0	0	0
Ms(0.4) =	0.442	1.748	5.385	12.918	24.133	35.113	0	0	0	0	0	0	0
	0.39	1.543	4.752	11.4	21.297	30.987	0	0	0	0	0	0	0
	0.268	1.06	3.266	7.835	14.637	21.297	0	0	0	0	0	0	0
	0.144	0.568	1.748	4.194	7.835	11.4	12.918	0	0	0	0	0	0
	0.06	0.237	0.729	1.748	3.266	4.752	5.385	0	0	0	0	0	0
	0.019	0.077	0.237	0.568	1.06	1.543	1.748	0	0	0	0	0	0
	- з (4.91x10	0.019	0.06	0.144	0.268	0.39	0.442	0.39	0	0	0	0	0

Рисунок 7 – Результат расчета матрицы Ms при А = 0,4

Figure 7 – The result of the calculation of the matrix Ms at А = 0,4

Программа вычисления значений функции распределения угла бросания представлена на рисунке 8.

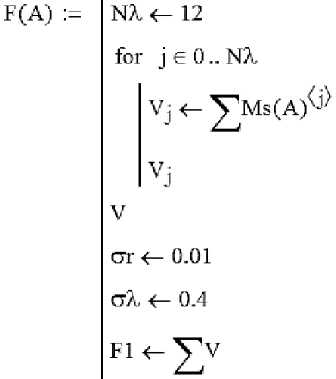
Ғ <-Ғ1-0.5-ог-0.5-сгХ

Рисунок 8 – Программа вычисления значений функции распределения угла бросания

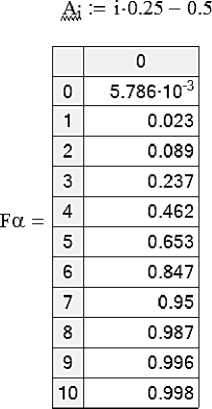
Figure 8 – The program for calculating the values of the distribution function of the angle of throw

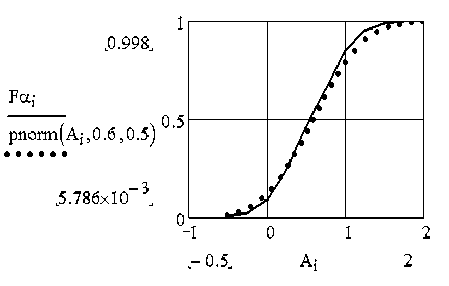
Рисунок 9 – Результат счета функции распределения угла бросания

Figure 9 – The result of the calculation of the distribution function of the angle of throw

Аппроксимация полученной функции распределения угла бросания стандартной функцией нормального распределения (рисунок 9) дает удовлетворительное совпадение графиков. Математическое ожидание угла бросания, полученное расчетом, соответствует оптимальному значению для двухдискового аппарата. Среднее квадратическое отклонение угла бросания меньше оптимального, равного 0,6 радиан. Увеличение его можно получить рассредоточением подачи по углу λ , например подачей удобрений через два туконаправителя.

Выводы. В исследовании предложена методика расчета функции распределения угла бросания удобрений центробежным аппаратом с отклоненными от радиуса лопатками как функции случайных координат точек подачи, рассмотренная на числовом примере. Полученная расчетом функция распределения угла бросания аппроксимирована стандартной функцией нормального распределения. Предложенная методика позволяет моделировать процесс распределения удобрений и семян. Так, например, в рассмотренном варианте математическое ожидание угла бросания получено близким к оптимальному для двухдискового аппарата. Среднее квадратическое отклонение угла бросания, полученное расчетом, меньше оптимального, поэтому рекомендуется повторить расчет для конструкции распределяющего диска с лопатками, отклоненными вперед на больший угол. Увеличение среднего квадратического отклонения угла бросания можно также получить рассредоточением подачи удобрений на диск, например, применением подачи через два туконаправителя. Плотность вероятности системы r,λ в этом случае надо вычислять по формуле суперпозиции двухмерных нормальных распределений.