Методика расчета упругих эффективных свойств двухфазных полидисперсных сред с использованием многоточечных статистических дескрипторов и метода интегральных уравнений

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2019PNRPU MECHANICS BULLETIN

Многие современные материалы, используемые в высокотехнологичных приложениях, обладают неоднородной микроструктурой. Неоднородность структуры материала может быть определена целью его применения либо являться результатом возникновения нежелательных дефектов, обусловленных технологическими особенностями процесса производства. Установлено, что влияние на эффективные характеристики материала оказывает не только объемная доля содержащихся в нем компонентов, но и морфологическое строение микроструктуры. В связи с этим актуальной проблемой механики неоднородных сред является установление взаимосвязи между конфигурацией микроструктуры и механическими и физическими свойствами, реализованными в материале. В частности, необходимо развитие методов математического моделирования, способных оценить поведение неоднородных материалов на различных масштабных уровнях. Предсказание макроскопических свойств композиционных материалов сопряжено с необходимостью достоверного описания их микроструктурного поведения, включая взаимодействия между отдельными компонентами. В целом для создания эффективной методики с целью определения макроскопических свойств структурно-неоднородных сред необходимы:

– геометрическая модель микроструктуры, для которой можно в явном виде произвести численный расчет с учетом ее геометрии и свойств компонент;

– механическая модель, с достаточной точностью описывающая взаимодействие распределенных компонент и окружающей их матрицы.

К настоящему времени разработан ряд аналитических и численных подходов для оценки эффективных свойств структурно-неоднородных сред. Одним из основополагающих исследований в области определения эффективных свойств неоднородных сред является решение для единственного эллипсоидального включения, полученное в работах Эшелби [1]. Границы эффективных свойств упругих неоднородных сред на основе вариационных принципов были получены в работах Фойгта и Рейсса, Хашина и Штрикмана [2], Берана [3]. Многие подходы базируются на методах среднего поля, впервые появившихся в середине 20-го века. Эти методы предлагают ряд алгоритмов для определения упругих констант, например метод Мори-Танака [4], метод двойного включения [5], а также другие [6–8].

Методы гомогенизации для нелинейных композитов берут начало в работах Тейлора и Хилла [9], в которых рассматривалась проблема определения макроскопического поведения пластически деформируемых поликристаллов. Самосогласованные модели применительно к упругопластическим композитам были пред- ложены Е. Кренером [10], Б. Будянски [11] и Р. Хиллом [9], в которых предполагалось постоянство пластических деформаций. Позднее Дж.Р. Уиллисом [12] было получено нелинейное обобщение границ Хашина– Штрикмана.

П. Понте-Кастанедой [13, 14] были предложены новые вариационные подходы, позволяющие улучшить оценки границ и получить более общие решения для нелинейных сред. Некоторые авторы предлагали модификации схем Мори-Танака для учета произвольно ориентированных эллипсоидальных включений [15], а также для волокон с заданной функцией распределения ориентации [16], в том числе их реализацию для упругопластического случая [17].

С развитием вычислительных возможностей появились работы, позволяющие производить расчет эффективных модулей для представительного объема путем прямого решения методом конечных элементов [18-20]. Несмотря на достигнутые успехи, прямой конечно -элементный расчет представительных объемов для определения эффективных свойств сильно зависит от качества и густоты сетки и достаточно затратен в плане вычислительных ресурсов при исследовании структур со случайной ориентацией и сложной геометрией включений.

В отдельную задачу входит определение минимально допустимого размера представительного объема [21-25]. В работах Севостьянова и Качанова [26-28], а также Бема [29-32] и других [33-35] установлено влияние формы неоднородностей на макроскопические свойства.

Другая группа аналитических моделей для определения макроскопического отклика неоднородных материалов базируется на использовании многоточечных статистических дескрипторов. Трехточечные оценки термоупругих свойств двухфазных материалов на основе набора многоточечных корреляций были получены в работах С. Торквато [36,37], при этом удалось получить границы, находящиеся внутри границ Хашина– Штрикмана. В отечественных работах в данном направлении широко распространен подход, получивший развитие в работах Т.Д. Шермергора и С.Д. Волкова [38, 39] и позволяющий определять макроскопические модули, а также структурные поля деформаций и напряжений в композитах стохастической структуры. Так, для исследования структурных полей деформирования и расчета эффективных характеристик микронеодно-родных сред решаются стохастические краевые задачи, уравнения и граничные условия которых содержат случайные величины. Исходное стохастическое уравнение с помощью функций Грина преобразуется в интегро-дифференциальное, которое решается приближенно методом итераций. Результаты приближенного решения зависят в первую очередь от вида координатной зависимости статистических дескрипторов структурных модулей упругости. При этом используются различные предположения:

• -    сингулярное приближение, которое заключается в том, что в интегральных уравнениях равновесия, ядрами которых являются вторые производные тензора Грина для изотропной неограниченной среды, удерживаются только сингулярные составляющие этих производных [38]. С помощью обобщенного сингулярного приближения, изменяя параметры, как частный случай можно получать различные приближенные решения для эффективных упругих констант (границы Фойгта, Рейса, а также Хашина-Штрикмана);

• -    гипотеза сильной изотропии в том смысле, что макроскопические характеристики композита не зависят от многоточечных моментных функций структурных модулей упругости [40-42];

• -    предельная локальность моментных функций структурных модулей упругости: ограничиваются учетом дисперсий моментных функций [43];

• -    корреляционное приближение основано на пренебрежении моментами выше второго порядка. В общем случае корреляционная теория может быть применена при малых флуктуациях структурных модулей упругости, т.е. когда среднеквадратичные отклонения структурных модулей упругости являются малыми по отношению к их математическим ожиданиям [39, 43];

• -    одноточечное приближение является уточнением корреляционного приближения за счет использования одноточечных моментов всех порядков. С помощью одноточечного приближения нельзя описывать анизотропию свойств композиционных материалов, связанную с ориентацией включений, например, матрицы с ориентированными эллипсоидальными включениями.

Таким образом, в большинстве работ инструментарий описания стохастических структур ограничивается, как правило, статистическими дескрипторами второго порядка, которые во многих случаях принимаются равными постоянным значениям.

В данной работе для расчета эффективных характеристик предлагается использование многоточечных приближений решений краевых задач, в которых необходимым является учет в явном виде моментных функций высших порядков, что позволит в более полной мере учитывать многочастичное взаимодействие микроструктурных элементов. Использование высших приближений решений даст возможность уточнить границы, полученные с использованием описанных выше допущений.

1.    Аналитические выражения для эффективных констант

Будем считать, что микроструктурные компоненты двухфазной среды являются изотропными, т.е.

С = Х 1 5 , 5 _й +ц i ы5 , + 5_Й 5 ,к ) ,

C M =^ м 5 , 5 _н +ц м ( 5_ft5, + 5 5 , _к ) , (1)

где нижний индекс I обозначает включения; M - матрицу; C’кM - тензоры структурных модулей упругости; 5j - дельта Дирака; Xz, XM, ц, цм - постоянные Ла- ме и модули сдвига включений и матрицы соответственно, выражаемые через модуль упругости и коэффициент Пуассона как

1        Ei V

А, =-----------------, ц, =

I   (1 + v у )(1 - 2 v у )   ^

—^—,    (2)

2(1 + v у )          '

где E_z - модуль упругости включения; v₇ - коэффициент Пуассона. Аналогично для Х_м и ц_м .

Макроскопические деформации £ * и напряжения G * определяются путем осреднения по элементарному макрообъему V :

^е> г b j ⁽ r "dV ,

₁ ^V                                  (3)

^g * - =tJ^g j ⁽ r ) ^dV •

VV

Поля микроструктурных напряжений g_z ( r ) и деформаций £у . ( r ) являются случайными, зависят от пространственного радиуса-вектора r и представляют собой кусочно-постоянные функции координат. При моделировании неоднородных структур со случайным разбросом включений, как правило, принимается гипотеза эргодичности, согласно которой осреднение по объему совпадает со статистическим осреднением:

^£>к^£ iAr ^=k^e «V ⁺(^е j L ⁽¹ - p ), ^G =(^G j ⁽ r )) = V \ p ⁺ V L ⁽¹ - p )•

В общем случае, когда Gy = ^у /_z Р + \°_у /_м (1 - Р ), а р - объемная доля включений, эффективные константы упругой неоднородной среды могут быть получены из решения системы линейных уравнений

^G j =W r )) = Wp ⁺ Ы)м ^{(1 -} Р ) = C i i ki e ki ’  ⁽⁵⁾

где CУы - тензор эффективных модулей упругости, компоненты которого находятся по формуле Ci. = X5ij5ki + о(5«5ji + 5и5jk) ; eij - компоненты постоянного заданного симметричного тензора малых макродеформаций, определяющего нагрузку представительного объема.

В случае пористых материалов последнее уравнение сводится к следующей зависимости:

(^G^m ⁽¹ - P ) = C i y ki e ki •

При вычислении структурных деформаций и напряжений используют явные представления поля

Cyk /( r ) через постоянные тензоры модулей упругости элементов структуры (1) и случайную индикаторную функцию X ( r ) , которая принимает значения 0 или 1 в зависимости от положения радиуса-вектора внутри представительного объема:

C jki ( r ) = А ( rtj + (1 -А ( r))C “_H ,         (7)

CIM и C - тензоры модулей упругости включений и матрицы соответственно.

Выражения для средних значений напряжений и деформаций в матрице могут быть получены на основе формул для условного математического ожидания, представленных в [39]:

(^G j-X = (^GeV 1 - p X'⁽ r ^)g V ⁽ r ))’        ⁽⁸⁾

(^G j \ =(^G nV ” Vrr ^)g ‘j⁽ r )),          ⁽⁹⁾

где X’ (r), G‘(r ) , ^kI (r) и u‘ (r ) являются флуктуациями полей случайной индикаторной функции, напряжений, деформаций и перемещений соответственно. В общем случае флуктуации случайной величины Z в точке r определяются как Z(r) = Z(r)-(Z(r)), где ^ - оператор статистического осреднения. Выраже ние для статистического момента второго порядка ^ X’ (r )gz’. (r )^ , содержащего флуктуации индикаторной функции и поля напряжений, выражается следующим образом [44-46]:

(X’( r ) g’ ( r >) = e ki C jki D^' - C jki (1 -2 P )x

x(X’( r ) _£ ki ( r )) + C^_ijH ) (X'( r К ( r )),         (10)

где ^C mnkl = C Inki ^- C Mnki ^- разность тензоров структурных модулей упругости включений и матрицы ; D ⁽²⁾ =(X’ ( r ) X’ ( r )) = p (1 - p ) - центральный момент второго порядка (дисперсия) случайного поля индикаторной функции, выражаемый через объемную долю включений.

Тогда, с учетом соотношения (5), общее выражение для компонент тензора эффективных модулей упругости принимает следующий вид:

Cijki = pC‘H + (1 - p) CMi +(Cjki - CM )^X(r )£h (r ^, (11) ekl eki (r) = 1 [ uk( X *( r) + u%)(r)] •            (12)

Считая макрооднородный представительный объем неоднородной среды изотропным, достаточно опреде- лить только две его упругие константы. Так, учитывая, что для изотропного тензора эффективных модулей упругости ц* = C*212, значение эффективной константы можно получить из решения задачи о чистом сдвиге.

^Ц = C 1212 = p^C 1212 ^{+ (1}   p ) C 1212 ⁺

IM

⁺ ( ^1212   ^1212 )

(^X' ^{( r} ХД r )) e 12

Значение второй эффективной константы находится из решения задачи о всестороннем растяжении:

X * = C *111 - 2 ц * ,                   (14)

C m = PC™ + (1 - p ) C M 11 + ( С ш - C M" /^{X ( r ) £ 11( r} ^ . (15) ^e 11

Таким образом, эффективные модули согласно предложенному методу определяются как сумма их средних значений и уточняющей добавки, связанной с упругими многочастичными взаимодействиями между неоднородностями. Для вывода аналитических выражений для смешанного статистического момента второго порядка ( ^{X1 ( r} >ki ^{( r} )) , определяющего величину данной добавки, в данной работе предлагается использовать приближенные решения стохастической краевой задачи относительно перемещений, представленные в виде интегродифференциального уравнения и полученные на основе метода функций Грина.

• 2.    Приближенные решения для эффективных констант на основе многоточечных статистик

Как показано в работах [44–48], стохастическая краевая задача теории упругости для структурнонеоднородных сред с помощью функции Грина сводится к интегродифференциальному уравнению относительно флуктуаций перемещений:

u. j ^{) ( Г} ) = J ^G im ,j ( ^Г ’ ^Г 1 ) ^X

V 1

x( C' mnkl ( Г 1 ) e_k i + C m» ( r ) u'_k (?^-1) ( ^ ) j , 1 „ dV     (16)

где Gm (r, г) — функция Грина; Cm^ (r) - флуктуация поля структурных модулей упругости; r – обозначение k-й компоненты радиуса-вектора r ; , j - обозначение производной %  ; х - приближение, в котором ре

/ 9 r1 j шается задача.

Форма данного уравнения предполагает его итерационное решение. В первой и второй итерации решения уравнения (16) принимают следующую форму:

U1j7r) = eklCmnkl J Gim,j (r, r )l X1 (F1) 1,1[„]dV(17)

V1              VJ

UT ²⁾( ^r ) = e kl C mnkl J ^G im , j ( ^r ’ r ) l ^X' ( r ) 1 ’ 1[ n ] ^dV ⁺

V            V7

+ e С oq mnkl fsoq J J   im, j \ ’ 1 /

V V 2

X X(r1 ) Gkf,l (r1, r2 )lX (r2) 1,2[s]  ,1[n] dV2dV1, где X‘(r) = X(r) — (X(r)^ - флуктуация случайной индикаторной функции в точке; uk z(r) - поле флуктуаций перемещений в представительном объеме, которое является решением краевой задачи теории упругости в стохастической постановке. Выражения для момента (X1 (r )Е'„ (r )} с использованием решений (17) и (18) выражаются в следующем виде:

(X‘ ( r ) е j ( r )}⁽¹⁾ =

= ¹ e kl C mnkl J ( ^G im,j ( r , ^r 1 ) ^{+ G} jm , i ( r , ^r 1 ) ) ⁹ ^ X, ⁽ r ’ r " ) ^dV 1 , ⁽¹⁹) ²            V 1                                             ^{9 r} 1[ n ]

(^X‘ ( r ) £'. ⁽ Г ))^{<1 + 2)} =

= 1 eklCmnkl J (Gim,j (r , r1 ) + Gjm,i (Г , Г, )) 9KX  (r’ r1^ dV1+

² V          V                                        ^{9 r} 1[ n ]

⁺ e oq C fsoq C mnkl J J ( ^G im,j ( ⁷ , rv ) ⁺ G m , i ( r , r j ) ) ^X

,     . Я2K(i)(r г г}X xGkf,l (r7r2)9 KX (?r1’r2) dV2dV1 .

9 Гг n ]9r2[ s ]

Второе слагаемое в скобках в выражении (20) является добавкой, вносимой вторым приближением (18) к решению в первом приближении (17).

Перемножение флуктуаций индикаторной функции приводит к появлению в выражениях в явном виде корреляционных и моментных функций, которые используются для оценки пространственного взаимодействия между микромасштабными структурными компонентами [49]. Моментная функция n -го порядка может быть определена как среднее скалярного произведения n случайных величин в различных положениях радиусов-векторов r , r ’..., r . Для флуктуации случайной индикаторной функции выражение для моментной функции в целом можно записать в виде

K X n ) ( r , ?_x,_ r_n ) = Гj)X¹< r₂)...X'(r„)} =

= (( ^{X ( r) -} P )( ^{X (} r) ^- P ) ... ( ^{X (} r n ) ^- P )) . ⁽²¹⁾

Моментные функции чувствительны к таким параметрам, как распределение, ориентация и форма микроструктурных составляющих. Теоретически микроструктурная морфология композитов может быть однозначно определена бесконечным числом моментных функций. Эти функции в том числе используются в качестве гео- метрических характеристик в задачах получения статистик высоких порядков для микроструктурных полей напряжений и деформаций [45].

Возвращаясь к расчету эффективных констант, в явном виде значение смешанного момента

(X‘( r )е‘₂ ( r )) в выражении для эффективной константы

*/1<»\ ц (13) с использованием первого приближения (19)

и с учетом свойств симметрии входящих в него тензо- ров записываем как

Л

,   1

= 2 х — e₁₉

2 12

( ^X‘ ⁽ r     r ⁾/ ¹⁾ =

C 1212 J⁽ G 11,2 ( ^Г , r i ^{) + G} 21,1 ^{( Г} , r ) )

V dK^ri)

V

d K < ²⁾( r , ГУ)

⁺ C 2112 J ⁽ G 12,2 ⁽ r , r ) ⁺ G 22,1 ⁽ r , r ) )

V dr1[1]

^{д r} [2]

dV +

dV 1  .(22)

)

После преобразования получаем

( ^X‘ ⁽ r ^V r ^ =

= ² e 12 ^C 1212 J⁽ G 11,2 ⁽ r , r ^{) +} G 21,1 ⁽ r , ^Г 1 ) )     7        ^dVV  ⁽²³⁾

V                                        ° ^Г 1[2]

Добавка, вносимая вторым приближением в (20), выражается следующим образом:

( ^X‘ ⁽ r ^ r ^ =

= 4 e 12 C 1212 C 1212 J J ^{( G} 11,2 ⁽ r , r ) ^{+ G} 21,1 ⁽ r , r ) ^{) х}

V V 2

X G 112 ( г ) ^{5 2} K ' ' Г , r , r' dV dV        (24)

^{d r} 1[2] ^{d r} 2[2]

Таким образом, эффективная константа ц* может быть определена как сумма среднего по представительному объему значения компоненты тензора ^ C ₁₂₁₂( r )^, а также двух слагаемых, которые являются уточнениями, вносимыми первым и вторым приближением решения уравнения (16) соответственно:

Ц * = C 1212 = pC^ + (1 - Р ) С Ш2 +

+ 2 ( C^ - О ) ² J ( G „,₂ ( r , Л ) + G^ ( r , r_x ) ) ^{д К}&) 1 ) dV +

V 1                                         ^{d r} 1[2]

^{+ 4 ( C} 1212 - ^C 1212 ) J J ^{( G} 11,2 ⁽ r , r ^{) + G} 21,1 ⁽ r , r ^{) ) х}

V V

X G 11,2 ( r ,Г ) ^{d 2} K " ³⁾⁽ r , r ¹ , dV 2 dV 1 .         (25)

^{d r} 1[2] ^{d r} 2[2]

Для определения эффективной константы X * шем в явном виде момент ^X‘( r )s₁‘₁ ( r )^ :

запи-

(^{X ( r ) s} 11 ^{( r} ))         ^e 11 ^C 1111 J ^{( G} 11,1 ^{( r} , ^r 1 ) ^{+ G} 11,1 ^{( r} , ^r 1 ^{) ) х}

²        V

X ^{d K X2> ( r} , ^{r 1 )} dV 1 + 1 CuC _22И X a / 1,1]               ²

^X J ( ^G 12,1 ( r , ^1 ) ^{+ G} 12,1 ( r , ^1 ) ) ^ K X^ r l r l) ^dV 1 +

V 1                                           ^{d r} 1[2]

+ ¹ C 11 C 33H J ( G 13J ( r , >= 1 ) + G 13,1 ( r , Г 1 ) ) ^{d K}\^(r , r ¹ ) dV 1 . (26)

• ²          V                                     ^{d r} 1[3]

После упрощений данное выражение приводится к виду

(^X‘ ⁽ r ⁾ e‘ 1 ⁽ r ⁾/ ^1> =

= C 11 Z C mn _и J G 1 m ,1 ( r , r_x ) ^{d Kr} , r ¹ ) dV 1 .     (27)

m = n =1        V                     ^{d r} 1[ n ]

Аналогичным образом находится добавка, соответствующая второму приближению решения:

X X‘ ( r ) ^е1 1 ( r >y² > =

• 3    3   -   -    _{r r}

= e11 Z Z Cfs 11 Cmn11 J J G1 m ,1 ( r, r! )x f=s=1 m=n=1

xGin(r,r2)9 K")(r,r1,r2)dVdV,.

1 fJ (1 2)    dгц n ]dr2[ s ]       21V 7

В окончательно виде формула для эффективной константы X * принимает вид

X * =- 2 ц * + pC‘ 111 + ( 1 - p ) CM 11 +

+ ( C*111 - CMu )Z( CIn 11 - CmMn и )x m=n=1

X J G 1 m ,1 ( r , Z j ) ^{d K}"'(r-^r , r ¹) dV 1 +

V                     ^{5 r} 1[ n ]

+(c, I,,, -с“Л у у (c'„ -c M Jfc I -c M Jx

У 1111      1111 у / J / J \ fs 11      fs 11      mn11      mn11 / f=s=1 m=n=1

X J J G 1 m ,1 ( r , Г 1 ) G 1 f ,1 ( lA ) ^{d 2 K X 3) (} r ’ r ^{1 ,}r ² ) dV ₂ dV 1 . (29) V V₂                                      ^{d r} 1[ n ] ^{d r} 2[ s ]

Таким образом, особенностью метода последовательных приближений является возможность уточнения значения эффективных констант в зависимости от морфологических особенностей, выражаемых через структурные моментные функции. Из выражений (19) и (20) видно, что каждое последующее приближение зависит от структурной моментной функции более высокого порядка, что позволяет в более полной степени учитывать морфологию микроструктуры в необходимых случаях.

3.    Численная реализация метода

Для численного решения интегралов, входящих в полученные уравнения, необходим явный вид функции Грина. Когда размеры представительного объема много меньше характерных размеров твердого тела, в случае изотропной среды в качестве функции Грина Gkn (r, r) для трехмерного пространства в работах [10, 38] было получено следующее выражение:

G kn ( r ’ r ) =

1 --—7----7 X Hh> r ^— r i|

X

(x)+(3ц)       (X)+W

------Г ⁵ kn ⁺ X”TTi ------J r ^— r kk ]^{)( r} n ^— r n ]) •⁽³⁰⁾

(X + 2ц)       8 п\ц)(1 + 2ц)                _?

При этом (X) = X iP + X M (1 ^— p ), (ц) = ц i P + ц M ⁽1 ^— p )•

Для вычисления интегралов, входящих в выражения (25) и (29), необходимо использовать методы численного интегрирования. Интегрирование проводится по всей области статистической зависимости в сферических координатах, где координаты вектора r = r ( x , y , z ) определяются по формулам x = r cos ф sin 9 , y = r sin ф sin 9 , z = r cos 9 , 0 <  r <  a, 0 <ф< 2 n , 0 <9<п , где a -сторона представительного объема. Переход к сферическим координатам обусловлен избавлением от сингулярности функции Грина (30) по всем трем переменным декартовой системы координат и переходом к сингулярности только по одной переменной r . Для достижения допустимой погрешности интегрирования применяется глобальная адаптивная стратегия в совокупности с многомерным правилом интегрирования и правилом преобразования переменных IMT для обхода сингулярности.

Глобальная адаптивная стратегия основана на том, что из всех подобластей исходной области интегрирования выбирается подобласть с наибольшей погрешностью и делится пополам. Затем вычисляются значение интеграла и погрешность для каждой половины, и процедура повторяется для всего множества подобластей. После каждого такого шага пересчитываются глобальное значение интеграла и глобальная погрешность, которые представляют собой сумму значения интеграла и погрешности в каждой подобласти. Ожидается, что глобальная погрешность должна монотонно снижаться с увеличением числа областей.

Многомерное правило интегрирования [50] опреде ляется следующим образом. Для куба

2’2

d e N, d >  1 задается набор точек, удовлетворяющий следующим условиям: любая точка из множества может быть получена перемещением или заменой знака координаты любой другой точки из этого же множества; все точки множества имеют одинаковый весовой коэффициент. Множество точек, соответствующее вышеописанным критериям, называется орбитой. Если правило интегрирования имеет K орбит Q_T,Q₂, _ ,Q^, а i -я орбита Q. имеет весовой коэффициент w_t , интеграл приближенно вычисляется по формуле

K

J f ( X )d x < £ w ^ f ( X j ).

d                  i = 1     X j E Q i

' 2’2 ]

Преобразование переменных IMT предложено в работах Ири, Моригути и Токасава [51] и основано на идее преобразования независимой переменной таким образом, что все производные нового подынтегрального выражения обращаются в ноль в конечных точках интервала интегрирования.

В приведенном ниже примере выполнено численное сравнение результатов расчета относительных эффективных характеристик пористых неоднородных поли-дисперсных сред со сферическими включениями. Пример геометрической модели такой среды представлен на рис. 1, где красным цветом выделены включения (поры). Создание модели осуществлялось методом последовательного синтеза, согласно которому каждое новое включение помещается в произвольную точку внутри куба, при этом контролируется его пересечение с уже существующими включениями. В случае наличия пересечения данное включение отбрасывается и генерируется новое. В качестве включений использовались сферы различных радиусов, проверка пересечения между которыми осуществлялась путем расчета расстояния между центрами.

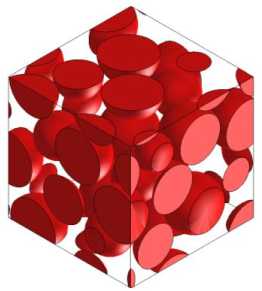
Рис. 1. Представительный объем полидисперсной неоднородной среды с объемной долей включений 40 %

Fig. 1. Representative volume element of a polydisperse heterogeneous medium with 40 % volume fraction of inclusions

Моментные функции, характеризующие неоднородную среду, получены на основе разбиения трехмерного представительного объема сеткой с фиксированным шагом и кубической формой конечного элемента (так называемая воксельная сетка). Преимущество использования такого способа получения значений моментных функций связано еще и с тем, что информацию о представительных объемах неоднородных материалов в таком виде легко получать из экспериментальных исследований, например, на основе микрокомпьютерной томографии.

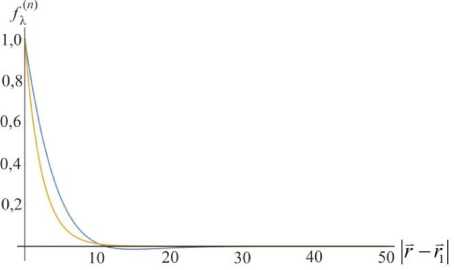
На рис. 2 изображены нормированные моментные функции второго и третьего порядка вида f ^{( n} ) (| r — r |) =

K X n ) (I r - r 1| )

_D ( n )

, где D ^ ⁿ )

– дисперсия n -го порядка ин-

дикаторной функции X ( r ) , полученные для изображен-

ной на рис. 1 среды и используемые в выражениях (25) и (29).

Моментная функция второго порядка

Моментная функция третьего порядка

На рис. 3 представлены значения отношения эффективных модулей X * и ц* среды к модулям матрицы. Данные величины являются безразмерными и изменяются от 0 до 1. Также приведено сравнение с границами Хашина–Штрикмана [2] и сингулярного приближения, предложенного Т.Д. Шермергором [38]. Границы Ха-шина–Штрикмана эффективных констант для двухфазной неоднородной среды вычисляются по формулам

₊      P 1 ( ^к 1 ^- k 2 )       < _к * <

1 +   ^p — ( k. - k ₂)

3k2 + 4ц v 127

< k +    P 2 (k 2 -^    ,(32)

1+— p — ( k - k )

3k + 4ц/ 217

Рис. 2. Моментные функции второго и третьего порядка для двухфазной неоднородной среды с объемной долей включений 40 %

Р 1 ( W -k ) ц +

1 + 6 p 2 ⁽ k ₂ + 2^ц ) ₍       )

¹  5ц ( 3 k + 4ц ) ^(ц 1   ^ц 2 )

<ц +

P 2 ( k ^-Ц 1 )

*

1+

⁶ P ( ^k 1 ^{+ 2}k ) 5ц ( 3 k + 4 k )

( Ц 2 ^-Ц 1 )

где константы с индексом 1 относятся к компоненту с более жесткими свойствами.

Fig. 2. Second and third order correlation functions for a two-phase heterogeneous medium with 40 % volume fraction of inclusions

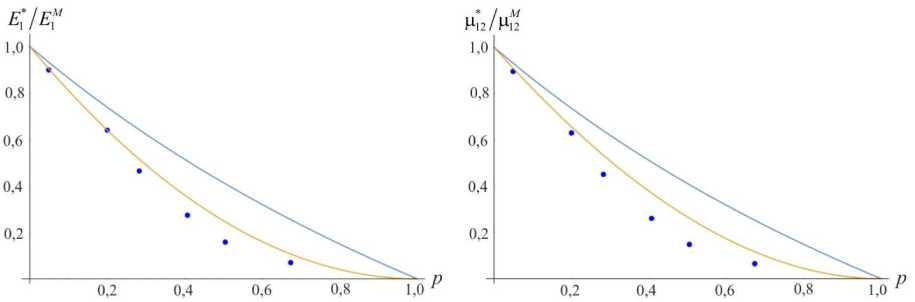
— Верхняя граница Хашина-Штрикмана

Верхняя граница сингулярного приближения

• Значение константы в первом приближении

Рис. 3. Значения эффективных характеристик среды, полученные в первом приближении, в сравнении с границами Хашина–Штрикмана и сингулярного приближения

Fig. 3. Values of the medium effective characteristics obtained in the first approximation in comparison with the Hashin–Shtrikman and singular approximation bounds

Сингулярное приближение основано на приведении решения к интегральному выражению, содержащему вторую производную функции Грина, и затем выделению сингулярной составляющей из нее, сводя таким образом интеграл по сингулярной области к постоянному тензору [38]. Согласно сингулярному приближению, точное значение эффективных констант находится в границах, образованных следующими неравенствами:

ц*

\^ц/  _п .            ц (9 к_г + 8 ц ) ^ц

(1- P )ц I + P ц M + /2   2/

6( к ₂ + 2 ц )

D

(1 - p )ц+ рцм+ 1  1—

IM

^{6( к} 1 ^{+ 2} Н 1 )

(9D---— s k • s

(1 - P ) ^k I + Pk M +J^ 2

^S WD¹----4- ,        (³⁵)

• ⁽¹ - P ) ^k I + P^k M + ^1

где    D ^ = p ⁽¹ - p ⁾⁽ ц i -ц m ⁾²;     D k = p ⁽¹ - p ⁾⁽ k i - k M ⁾²;

Ц 1 =(ц) ; Ц 2 =(ц ^{- 1}) ¹; k 1 = ( k ); k 2 = 1^k 1 •

Все изложенные результаты, включая численное интегрирование, получены в программной среде Wolfram Mathematica.

Как видно из результатов, использование предложенной методики с применением первого приближения позволяет уточнить значения эффективных констант для пористых структур с объемной долей выше 20 % по сравнению с сингулярным приближением, где не используется в явном виде информация о морфологии. Установлено, что для пористых структур с равномерным распределением включений добавка, вносимая вторым приближением решения, является несущественной. В то же время значимость этой добавки увеличивается с ростом отклонения распределения включений в представительном объеме от равномерного, который может быть обусловлен формированием кластеров, сильным разбросом размеров включений и т.д.

Заключение

В данной работе предложен метод вычисления эффективных характеристик полидисперсных неоднородных сред на основе применения многоточечных моментных функций и метода интегральных уравнений в виде приближенных решений стохастических краевых задач теории упругости. Входными параметрами данной модели являются упругие свойства компонент среды, а также формализованная в виде многоточечных моментных функций информация о морфологии среды. Полученные в явном виде выражения для эффективных констант мак-рооднородной изотропной среды представлены в виде средней составляющей и добавки, точность которой определяется приближением используемого решения и порядком входящих в него моментных функций. Инте-