Методика расчетного прогнозирования деформационных и релаксационных процессов полимерных материалов

Интенсивное развитие техники ставит перед материаловедением задачи получения новых материалов, повышения ресурсов работы традиционных материалов, разработки оптимальных режимов эксплуатации, создания методов прогнозирования работоспособности. Полимерные волокна, нити, пленки, а также композиционные материалы на их основе стали незаменимыми в изделиях бытового и технического назначения, деталях автомобилей и т.д. Эффективность производства полимерных материалов существенно зависит от развития соответствующих разделов материаловедения. Прежде всего, это достаточно глубокое количественное описание деформационных свойств в зоне действия неразрушающих механических нагрузок.

Существенное расширение областей применения и условий эксплуатации полимерных материалов требует качественного исследования их деформационных свойств. Такие исследования возможны на основе математического моделирования процессов деформирования. Поэтому разработка методик определения механических характеристик в условиях, отвечающих различным типам нагружения, является актуальной и важной задачей. Данная работа посвящена разработке методики математического моделирования и расчетного прогнозиро- вания деформационных и релаксационных процессов полимерных материалов.

Структура большинства известных полимеров как молекулярная, так и надмолекулярная достаточно хорошо изучена. Но на практике для количественного прогнозирования поведения полимерных материалов сегодня применяются различные методы математического моделирования [4,16]. В итоге имеются, с одной стороны, физические модели полимеров, а с другой стороны, основанные на линейных механических моделях методы математического моделирования, с помощью которых в настоящее время решается задача количественного прогнозирования свойств.

Но, как известно, все методы математического (расчетного) прогнозирования применимы в достаточно узком диапазоне механических нагрузок, деформаций и температур, и не позволяют, например, предсказать кривые изометрического нагрева и другие особенности поведения материала, поскольку они не учитывают внутреннюю структуру полимера. Кроме того, такие методы не охватывают и не объясняют все процессы, происходящие, в синтетических нитях и волокнах. Поэтому, основная задача работы [17] состояла в построении удобной для прогнозирования свойств в широком диапазоне нагрузок и температур физиче-

Методика расчетного прогнозирования деформационных и релаксационных процессов

полимерных материалов

ской и нелинейной механической модели, которая позволила бы учесть особенности материала.

При деформировании ориентированных аморфно-кристаллических полимеров особого рассмотрения заслуживает обратимая вязкоупругая составляющая деформации, которая, согласно современной физической картине может

появиться вследствие перестроек различных устойчивых структур (кластеров), находящихся

в состояниях, которые разделены энергетическими барьерами. Эти кластеры или, согласно принятой в работе [13] терминологии, активные конформационные элементы (АКЭ) могут находиться в двух устойчивых состояниях. Одно из устойчивых состояний с минимальным линейным размером – состояние 1 – буде м назы вать условно свернутым и обозначать . Второе устойчивое состояние 2 будем называть условно развернутым и обозначать .

Таким образом, предлагается вместо классических механических моделей в виде пружин, поршней и их комбинаций, то есть классических линейных элементов Максвелла, Кельвина-Фойгта и других, использовать нелинейную модель в виде упругой пружинки, основанную на энергетических барьерах, которые будем изображать следующим образом, представленным на рисунке 1 в виде энергетической

ется в математических моделях описания. Внешняя сила также оказывает активирующее действие на АКЭ, понижая или повышая потенциальный барьер на величину упругой энергии. В отличие от предыдущих работ учтено, что упругая энергия является квадратичной функцией от величины деформации.

В результате анализа всей системы описание реологического поведения одноосноориентированного полимерного материала можно свести к решению обыкновенного дифференциального уравнения, связывающего между собой деформацию е ( t ) (режим деформирования) и

ц ( t ) - усредненное механическое напряжение внутри. Окончательно, данную систему уравнений можно представить в виде:

—(е-ц) + (е-ц) fe d т

*2

*

‘ ™ +Ae "^

2 )=q о sh (yц 2),

t                                             1 H*

где: т = — - безразмерное время; т = — e

т p                        p V

– внутреннее время релаксации, определяемое

диаграммы.

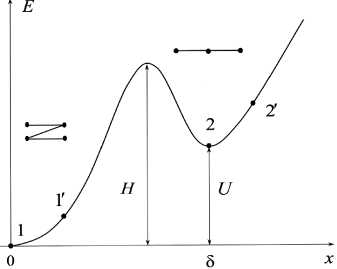
Рисунок 1. Энергетическая диаграмма АКЭ в зависимости от размеров кластера

высотой барьера; ц ( t ) = — - усредненное E 0

механическое напряжение, приложенное ко всему образцу, то есть величина, непосредственно определяемая из эксперимента; Y — структурно-чувствительный коэффициент, который определяется упругой энергией АКЭ,

* Y

Y = т - приведенный структурно

*

чувствительный    коэффициент;     A = e ;

2m A   2m q0 = ——0A и- - константа материала, слабо зависящая от температуры;

m ₀ = m p + m 2 = const - полное число АКЭ на единицу длины образца;

В ненагруженном состоянии кластер может находиться в двух устойчивых состояниях – либо в состоянии 1, либо в состоянии 2. Эти состояния разделены энергетической щелью шириной U и барьером высотой Н .

При переходе кластера из состояния 1 в состояние 2 высвобождается (рождается) квант деформации 5 и поглощается при противоположном переходе.

Состояния 1 и 2 характеризуются числами заполнения. В равновесном состоянии числа заполнения состояний 1 и 2 подчиняются статистике Л. Больцмана.

При этом температура повышает или понижает высоту приведенного барьера. Это дает количественное объяснение температурновременной аналогии, которая обычно использу-

p m p m

m: =---0-^ и m ^ =--- 0—, — числа заполне-

1 + e"U           1 + eU ния состояний 1 и 2 на единицу длины образца, подчиняющиеся в равновесном состоянии статистике Больцмана;

* Н * U

H * = — и U = U

k Á T

k Á T

– приведенная высо-

та энергетического барьера и приведенная ширина энергетического зазора, соответственно.

Уравнение (1) дает полное описание

процессов вязкоупругости в изучаемых одноосноориентированных полимерных материалах. Решение задачи Коши для этого уравнения требует задания начальных условий, а также вида режима деформирования, как например:

• 1.    Диаграмма растяжения ( ^е = ^const );

• 2.    Релаксация напряжения ( ^е = ^const);

• 3.    Ползучесть ( ц = const);

• 4.    Восстановление ( ц = 0).

Для изучения диаграмм растяжения, полученных с квазипостоянной скоростью де-

формирования

. d £

£ = — = const , применим оп- dt

щей из уравнения (1) при анализе процесса ползучести при условии ° = const , получаем выражение для времени релаксации, которое с учетом того, что t = 6 с, имеет вид:

ределяющее уравнение (1) к режиму активного растяжения. Считая £ малым параметром с точностью до £ в первой степени, решение уравнения (1) в общем виде для большинства высокоориентированных нитей и пленок можно

представить так:

т° =---,------г- , где £ и £p - значения де- ln I1 -А V p формации, полученные из эксперимента по ползучести для моментов времени 6 секунд и 10 минут.

Е, %               t^SOc

е( x)

... + £

x +

q [ 1 - e 2 ] ₊ 2 [ 1 + A e ’^Л2 ]

2 y q ( 1 + A ) e ^2v 2 x

1 + A e ’^v 2 ) 2 + 2 у q ( 1 + A ) e ^{- 2 Y} x 2 x учетом того, что вид диаграмм растя-

жения весьма слабо зависит от скорости де-

формирования, получим в предельном случае ( ^£ ^ ⁰ ) выражение для равновесной диаграм-

Ig (t/t,)

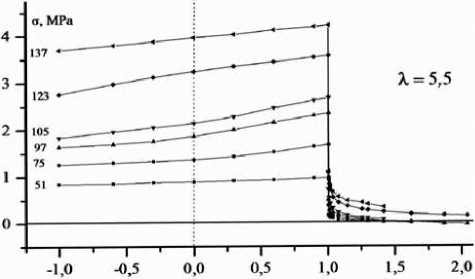
Рисунок 2. «Семейство» кривых ползучести с восстановлением ПКА пленочной нити предельной

мы растяжения:

£ = Ц +

1 - e ^{- 2 yV}

² [1 + A e ^-2^YV ]

степени вытяжки

С помощью полученного уравнения

можно прогнозировать точки диаграмм растя-

жения полимерных материалов в широком диапазоне деформирования.

Таким образом, для расчета точек диаграмм растяжения необходимо определить не-

известные константы, входящие в уравнение (3). Это возможно сделать, проведя экспери-

Из графика, представленного на рисунке 3, можно видеть, что зависимость времени релаксации от величины нагрузки имеет ярко выраженный максимум. Из полученной зависимости определяем координаты экстремальной точки, а именно максимальное значение времени релаксации т и соответствующее ° max

мент в режиме ползучести для исследуемого

ему значение механического напряжения °_max

полимерного материала.

Рассмотрим методику определения и расчета характеристик на примере поликапроа-мидной (ПКА) пленочной нити предельной z X = 5.5

степи вытяжки (     , ), полученной мето дом многоступенчатой зонной ориентационной вытяжки и исследованной в работах [14 – 15].

• 1.    Экспериментально получаем «семейство» кривых ползучести исследуемого материала (рис 2.).

• 2.    Определяем времена релаксации и строим зависимость этих времен от приложен-

• 3. Определяем значение углового коэффициента X .

Для этого вычисляем значения функции гиперболического арккосинуса отношения мак-

симального времени релаксации к текущему

Г Т ° ) arcch —— т„

^V ° ⁷ .И далее строим зависимость

°

-1

ного механического напряжения.

Так как время релаксации процесса ползучести порядка 1'', то за время t 1 = 6'' реализуется большая часть локальной ползучести, а за время t ₂ = 10' можно считать, что локальная ползучесть реализуется полностью, и деформация принимает равновесное значение. Тогда,

этой функции от выражения V °m 7    , кото рая для ПКА пленочной нити изображена на

рисунке 4.

Здесь ° - текущее значение напряже-т„ ния; ° - соответствующее этому напряже-

t

°_ = °„_

нию ° время релаксации; ^{m max} - значение напряжения, соответствующее максимуму

согласно формуле

^£ = ^£ p ^{1 -}e ^т

вытекаю-

функции Т ° .

V 7

Методика расчетного прогнозирования деформационных и релаксационных процессов полимерных материалов Для этого воспользуемся выражением для равновесного значения деформации при

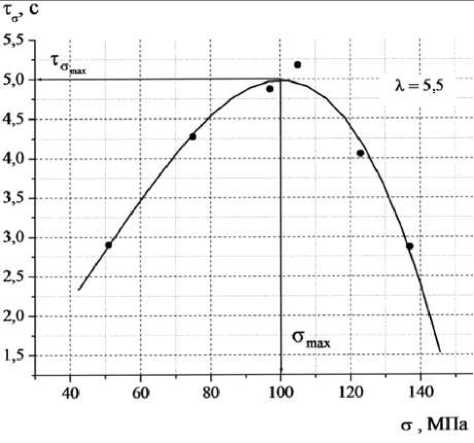
Рисунок 3. Зависимость времени релаксации процесса ползучести от величины нагрузки для ПКА пленочной нити

ползучести £ p = Ц +

q 0 (1- e2,V)

2 (1 + A e~2YV)'

*2   _2

Учтем, что ?Ц = ^a°

.

Выразим ^a , выполнив преобразования. ln A

Так как e

2   (—       a = —v

; a°m = AA  ^       2°m

учетом того, что lne2X 2X X

a = —T" = —т = —т

2  22

m mm

А = a2X,

. То есть

или с

a=°- m

получим

X

.

Запишем выражение для равновесной деформации, заменяя константы на полученные

значения. виде:

В результате получим уравнение в

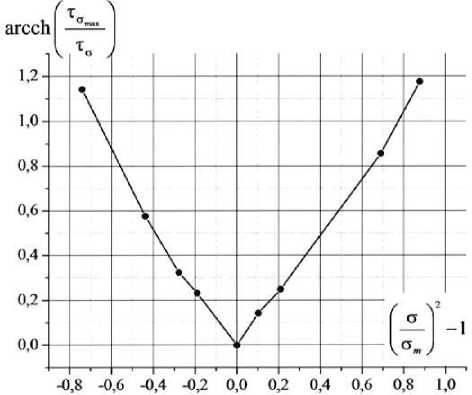
Рисунок 4. Зависимость гиперболического арккосинуса отношения максимального времени ре-

^£ р

О

=50+

q о ^{( 1}

^^^^^^^в

e - ² «° ² )

2 (1 + A e-1™")'

arcch

лаксации к текущему 2

I О ния ^V° m

Z =

I т„ ^ ° т„

^V ° ⁵ от выраже-

1                                            Z = 1"°") - 1

для ПКА пленочной нити    ^V ° m ⁵

Так

как

I О Y

-1

V ° m 5

.

та    ch (X 2)          ,=         = ch (X Z) и

^Т О    ^ch ( ^{X Z}m )

Численное значение X определяем как тангенс угла наклона кривой.

*

4. Определяем величину A = e^u

U*

С учетом того, что — = X , получаем,

А = а2Х.                2

что

5. Определяем константу материала q ₀ и модуль упругости Å ₀ .

Для того чтобы определить константу материала q ₀ и модуль упругости Å ₀ , запишем это выражение для двух значений деформаций и соответствующих им напряжений, взяв эти значения также из эксперимента по ползучести для момента времени 10 минут. В результате получим систему двух уравнений с двумя неизвестными, решив которую, найдем искомые величины.

6. Таким образом, все неизвестные, входящие в уравнение (3) и определяющие свойства исследуемого материала, определены. Это позволяет записать уравнение в явном виде и рассчитать точки диаграммы растяжения. Для ПКА пленочной нити со степенью вытяжки λ = 5,5 экспериментальная диаграмма растяжения _-

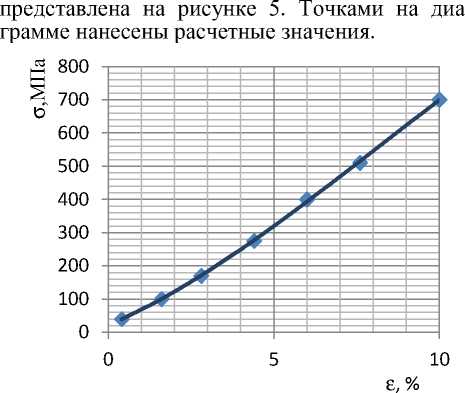
Рисунок 5. Диаграмма растяжения для ПКА пленочной нити предельной степени вытяжки X = 5,5

Как можно видеть из рисунка 5 расчетные значения хорошо согласуются с экспери-

ментальными данными. Расхождение составляет не более 10 %. Таким образом, предлагаемая методика применима для прогнозирования деформационного и релаксационного поведения полимерных материалов в широком диапазоне деформирования.

Следует отметить тот факт, что при расчете времен релаксации процесса ползучести возможен вариант, когда зависимость, изображенная на рисунке 3, не имеет явного максимума. А возможны варианты наличия либо правой, либо левой ветви зависимости. В этом случае определение коэффициента α упрощается.

Для этого воспользуемся общей формулой для времени релаксации τ _p

τ ⁼                 . Так как одно из слагае-

^σ e γ ^* µ ² ₊ A e -γ ^* µ ²

мых в знаменателе отвечает за прямые переходы, то есть переходы АКЭ из состояния 1 в состояние 2, а второе за обратные – из 2 в 1, то наличие одной ветви зависимости времени релаксации процесса ползучести от механического напряжения означает преобладание только одного типа переходов. Если, например, имеем только левую часть зависимости, то есть функция увеличивается с увеличением напряжения, то формула принимает вид τσ

τ p

. Или с e γ ^* µ ²

γ µ2 = ασ2

учетом того, что γ ^µ        , время релаксации

τp будет равно τσ =   2 , откуда после преобра- eασ зования получаем коэффициент ln τp

τ _σ

α =   σ σ2 . И далее определяем все метры, согласно предложенной методике.

α:

пара-