Методика расчёта антенн на основе уравнений Ампера и Фарадея

Теория антенн основана на законах Ампера, Фарадея, Кулона, уравнениях Максвелла, теории потенциалов и других положениях электродинамики. Особенностью этой теории является то, что она должна осуществлять связь теории поля с теорией общей (проводной) радиотехники. На самом деле этого не происходит. Исторически получилось так, что теория поля появилась раньше на полвека проводной радиотехники и поэтому законы и правила проводной радиотехники не принимались во внимание. Например, в теории поля и антенн совершенно игнорируется основная электродвижущая сила – напряжение . Во всех уравнениях – одни только токи, потенциалы, даже введены фиктивные токи – магнитные (в Махов Анатолий Иванович, кандидат технических наук, старший научный сотрудник, доцент кафедры радиотехники.

Вольтах). А ведь на антенну с генератора подаётся именно напряжение, а величина тока определяется возможностями антенны. Возникает вопрос: не нарушается ли при этом основной закон природы – закон сохранения энергии? Чтобы разобраться в указанных противоречиях, необходимо провести анализ уравнений теории поля, используемых в теории и практике антенн, на соответствие их законам природы, и при нарушениях этих законов предложить новую методику решения антенных задач. В этом и заключается цель данной работы.

ОСНОВНАЯ ЧАСТЬ

Исходя из выше сказанного, рассмотрим законы и уравнения теории поля, используемые в теории антенн [1– 4]. По закону Ампера магнитное поле создаётся любым сторонним током (проводимости, смещения), а согласно закону Фарадея электрическое поле создаётся изменением скорости магнитной индукции или как сейчас принято магнитным током.

Эти законы применительно к антеннам для монохроматического поля записываются уравнениями:

; (1)

ЭДС = ^_с dEf = ^- jw^H_CTS = ^- и_смст

. (2)

В левой части уравнений мы имеем магнитное и электрическое поля, создаваемые антенной в виде циркуляций векторов по произвольному замкнутому контуру C и названные магнитодвижущей силой и электродвижущей силой, а в правой части – сторонние силы, действующие на антенне и выраженные в различной форме. Форма, содержащая E _ст, H _ст предложена Максвеллом. I _ст – ток проводимости, I _смст – сторонний ток смещения ( по Максвеллу). Правую часть второго уравнения лучше назвать по аналогии с первым уравнением сторонним напряжением смещения U _смст (сейчас это магнитный ток в Вольтах!). Заметим, что индекс сторонних сил в правой части уравнений Ампера – Фарадея, даваемых в источниках [1 – 4] отсутствует.

Следует отметить, что эти уравнения позволяют определять параметры поля в разных точках пространства путём сравнения циркуляций векторов в разных его точках.

Уравнения (1),(2) удовлетворяют всем законам, проверены многочисленными опытами и не вызывают сомнения. На основе опытов и уравнений Ампера и Фарадея Максвелл открыл законы свободного электромагнитного поля и предложил соответствующие уравнения (без сторонних сил), названные его именем:

rot H = j ωε E + σ E;               (3)

rot E = – j ω μ H.                   (4)

Эти уравнения дают описание электромагнитного поля в произвольной точке пространства и показывают связь параметров поля – напряжённостей E, H – с параметрами ε , σ , μ среды, в которой существует это поле. Сторонние силы отсутствуют. Уравнения легко решаются в любой системе координат, если задано распределение поля на сравнительно простой поверхности (сфера, плоскость, цилиндрическая). В результате получено, что поле имеет волновой характер:

,             c коэффициентом распространения волны k=2π/λ и скоростью движения, сравнимой со скоростью света c = 3,108м/с. Установлено также, что векторы электрической E и магнитной H напряжённостей поля ортогональны друг другу и направлению движения волны, а их величины связаны между собой волновым сопротивлением           ; E = ZвH .

Это свойство электромагнитного поля можно назвать законом свободного поля. Согласно этому закону уравнения Ампера (1) и Фарадея (2) связаны между собой таким образом, что, если возникает магнитное поле, то тут же появляет- ся электрическое поле, влияющее на антенну и требующее соответствующей энергии от источника, и наоборот. Это – реакция среды в образе волнового сопротивления на излучение антенны. Причём, реакция эта – противодействующая первичному полю (знак минус во втором уравнении). Из уравнений также видно, что связь через волновое сопротивление имеется только между сторонними силами смещения: током смещения Iсмст и напряжением смещения Uсмст (напряжение проводимости в уравнении (2) отсутствует). Следовательно, можно предположить, что электромагнитное поле с волновым сопротивлением Zв могут создать только антенны, содержащие реактивные элементы. Активные сопротивления, включаемые в антенну, создадут только потери и сдвиг фазы между напряжением и током, поступающими на антенну. Из уравнений (3),(4) также следует, что для определения параметров всего поля достаточно определить левую или правую части уравнений (3),(4).

Рассмотрим далее уравнения Максвелла со сторонним электрическим током плотностью δ _ст : rot H – j ωε E – σ E = δ _ст= σ E _ст;       (5)

rot E = – j ω μ H .                    (6)

Эти уравнения часто используются в современной теории антенн [1] как общий метод решения антенных задач, причём иногда в уравнении (6) присутствует фиктивный сторонний магнитный ток.

Цель этих уравнений – получить математическим путём выражение вспомогательной функции ( векторный потенциал) для точечной антенны, на основании которого можно было бы строить сложные антенны. Результат получен только для ёмкостной антенны (диполь Герца), предполагая, что весь ток смещения протекает в узком коротком канале между шарами. Этот результат используют далее для реальных проволочных (уже не ёмкостных) антенн. Он непригоден для реальных ёмкостных и индуктивных ( ω L >> R) антенн, так как индуктивность и ёмкость не укладываются в уравнения в дифференциальной форме.

Обратимся далее к самим уравнениям (5),(6) и сравним их с уравнениями (1),(2).Предпола-гается, что уравнения (5),(6), как и уравнения (1),(2), полностью описывают ёмкостную антенну как самостоятельное устройство, на которое подаётся сторонний ток смещения δст. Стороннего напряжения смещения нет. Следовательно, на антенну не поступает мощность от генератора и тем самым нарушен закон сохранения энергии. Кроме того, нарушены ещё два закона электродинамики: закон Ампера и закон Фарадея. Действительно, из уравнений (5),(6) следует, что сторонний ток смещения создаёт не только вихревое магнитное поле согласно закону Ампера, но и ещё две векторные составляющие поля, что не подтверждается никакими экспериментами. Уравнение (6) вообще не содержит сторонних сил, следовательно, не может быть создано электрическое поле и тем самым нарушен и закон Фарадея. Согласно закону связи между напряжённостями стороннего поля в уравнениях (5),(6) должна присутствовать напряжённость Hст, а её нет. Далее эти уравнения решаются для антенны цилиндрической формы. Интегрирование ведётся не по сечению провода, а по всему объёму. При интегрировании по объёму антенны исчезает сечение проводника, то есть форма антенны не учитывается. Это неверно, так как параметры формы антенны должны присутствовать в результате решения уравнений. Согласно изложенному , уравнения (5),(6) к антеннам не имеют отношения, а решают полевую задачу определения влияния стороннего тока смещения на поле, созданное другой сторонней силой, которая остаётся неизвестной.

Таким образом, уравнения Максвелла со сторонним током непригодны для решения антенных задач. Очевидно, что решать эти задачи нужно с помощью уравнений (1) – (4). Необходимо также чётко определить само понятие – Антенна. Это определение следующее.

Антенна – проводное или волноводное устройство, занимающее определённый объём пространства, имеющее форму и поверхность излучения (поверхность, расположенная в непосредственной близости от поверхности антенны). На антенну поступает электрическая энергия, то есть сторонние силы: напряжение U_ст и ток I_ст. В результате в объёме, занимаемом антенной, образуется электромагнитное стороннее поле E _ст , H _ст в соответствии с правой частью уравнений (1),(2), а на поверхности излучения антенны формируется свободное электромагнитное поле E , H в соответствии с левой частью этих же уравнений. Следовательно, внутри антенного объёма действуют сторонние силы по законам проводной и волноводной техники, а на поверхности излучения и в остальном пространстве образуется свободное поле, действующее по своим законам и в соответствии с уравнениями (3),(4) Максвелла. Поверхность излучения является связующим звеном между полем внутри антенны и полем в пространстве вне антенны. Таким образом, задачей антенны является формирование свободного электромагнитного поля на поверхности излучения, а, следовательно, и во внешнем пространстве.

В случае волноводных антенн поле внутри волновода Eст, Hст(которое считается известным) непосредственно преобразуется во внешнее поле на поверхности излучения (щели), причем один из векторов является общим, то есть Hст= H (например, щель в боковой стенке, прерывающая ток), или Eст= E (щель – конец волновода, где действует напряжение), а другой вектор определяется по закону свободного поля E = ZвH. За- метим, что поле Eст, Hст в волноводе формируется с помощью другой антенны, либо генератором внутри волновода.

В случае проводной антенны, являющейся двухполюсником, при формировании поля работают: комплексная проводимость этого двухполюсника Y= G + jB в уравнении (1) и реактивная часть комплексного сопротивления этого же двухполюсника Z= R + jX в уравнении (2), определяемые типом, конкретными размерами и формой антенны. Таким образом, уравнения (1),(2) применительно к поверхности излучения будут иметь следующий вид:

I изл = H ср ℓ H = j ωε E ст S + σ E ст S = (G + jB)U ст ; (1а) U изл = E ст ℓ E = – j ω μ H ст S = – U смст = – jXI ст .   (2а)

Здесь Hср , Eср – средние значения напряжённостей поля на поверхности излучения. Левую часть уравнения (1а) на поверхности излучения предложено назвать током излучения Iизл(в Амперах), а левую часть уравнения (2а) на той же поверхности – напряжением излучения Uизл (в Вольтах). В настоящее время эти величины называют магнитным током Iм= HℓH(в Амперах) и электрическим током I= EℓE(в Вольтах!). Если ещё правую часть уравнения (2а) назвать магнитным током (в Вольтах) то налицо явная путаница.

Таким образом, в правой части уравнений (1а),(2а) имеем входные параметры антенны: сторонние напряжение Uст и ток Iст , поступающие с генератора, а в левой части – выходные параметры: напряжение Uизл и ток Iизл излучения на поверхности излучения. Всё ясно и понятно. Работа, например, реактивной антенны происходит следующим образом. При подаче на антенну напряжения Uст (назовём его активным) возникает реактивный ток (ток смещения) jBUст , который в соответствии с уравнением (1а) создаёт магнитное поле HℓH на поверхности излучения. Согласно закону свободного поля E = ZвH на поверхности излучения должно быть создано электрическое поле EℓE. Для этого на антенну поступает активный электрический ток Iст, который в соответствии с уравнением (2а) создаёт реактивное напряжение смещения jXIст= Uсм и требуемое электрическое поле Uизл=EℓE

В результате решения уравнений (1а),(2а) получаем распределение свободного поля H и E на поверхности излучения, сопротивление излучения R_изл= U_изл/I_изл, мощность излучения P_изл= 0,5I_излU_изл, вектор стороннего тока I _ст (если задано напряжение U_ст) и входное сопротивление антенны Z вх = U ст / I ст .

По известному полю E,H на поверхности излучения решается задача определения поля в пространстве (внешняя задача). Обычно пространство делят на дальнюю и ближнюю зоны, и требуется определить параметры полей в этих зонах. Деление пространства на зоны весьма условно, здесь учитываются расстояние r, размер b антенны и длина волны λ. Обычно дальней считается зона kr >> 1, если размеры антенны соизмеримы с длиной волны λ , а при размерах b антенны значительно меньших λ дальней зоной считается r >> b . Для дальней зоны антенну полагают элементарным источником электромагнитного поля ( размеры антенны << λ ) и расчет поля антенны в точке М пространства проводят по уравнениям (1),(2) путём сравнения циркуляций векторов поля в этой точке и на поверхности излучения. Элементарные источники известны и рассмотрены, например, в [5]. Их три типа: линейный вектор напряжения излучения Uизл (в работах [2 – 5] – это вектор электрического тока Iэ в Вольтах!) , линейный вектор тока излучения Iизл (в работах [2 – 5] – это вектор магнитного тока Iм), и элемент Гюйгенса, состоящий из двух названных векторов, находящихся в одной плоскости, ортогональных друг другу, и связанных между собой законом свободного поля E = ZвH. Известно, что силовые линии элементарных источников (линии равных напряжённостей) суть окружности, что и позволяет рассчитать поле этих источников. После выполнения амплитудных расчётов в результат добавляют фазовый множитель e–jkr в соответствии с теорией свободного поля. Диаграммы направленности первых двух элементарных источников – поверхности тора, а элемент Гюйгенса имеет шаровую диаграмму направленности.

В ближней зоне или при наличии сложной поверхности излучения поле антенны определяется путём интегрирования полей элементарных источников по соответствующим линиям поверхности излучения с учётом фазового множителя. Рассмотрим далее примеры расчета реальных антенн простых форм в дальней зоне.

1. ЩЕЛЕВАЯ ПЛОСКАЯ АНТЕННА, рис. 1

Щель длиной a < λ/2 и шириной b < λ/4 прорезана в боковой стенке волновода вдоль его оси (прерваны линии тока). Следовательно, имеем в щели поля: поперечное H = Hст и продольное E = ZвH, с почти равномерным распределением. Строго говоря, поля H и Hст могут быть неравными. Всё зависит от конфигурации полей в волноводе, и если она известна, то по уравнению Фарадея определяется вектор E а затем и H. Поле в волноводе: Hст,Eст – считается известным. Значения параметров поля в пространстве определяются уравнениями, следующими из (1а),(2а):

i Hdl = 1_ИЗЛ = Hb ,       (7)

'c

• £ Edi = U_H3J1 = Ea .        (8)

Jc

В правой части уравнений имеем два линейных вектора излучения, связанных между собой соотношением E = Z_вH, а силовые линии суть окружности, касательные к этим векторам [5], что для дальней зоны соответствует элементу Гюйгенса. Каждый вектор создаёт своё поле в точке М, поэтому уравнения для поля H в точке М на нормали к центру поверхности щели запишутся так:

H_м1πr₀ = Hb , H_м2πr₀ = Ha, которые следуют из уравнений (7),(8) применительно к элементарным источникам с учётом связей E_м = Z_вH_м и E = Z_вH. Здесь r₀ – расстояние от центра антенны до точки наблюдения М на нормали. Определяя далее H_м1 из первого и H_м2 из второго уравнений и суммируя результаты, получаем H_м0= H(a+b) /πr₀, E_м0= Z_вH_м0. Для поля по любому другому направлению α относительно нормали к поверхности щели и с учётом равенства H_м = H_м0 и фазового множителя имеем: Нм = H(a + b) cosae^-7/"7^Kr; Em = ZbHm.

Таким образом, получена шаровая диаграмма направленности, как и следовало ожидать.

Параметры антенны: мощность излучения P_изл= 0,5 EHab , сопротивление излучения R_изл= Z _вb/a , КПД = 100% , так как потери в среде и вследствие поверхностных токов не учитывались.

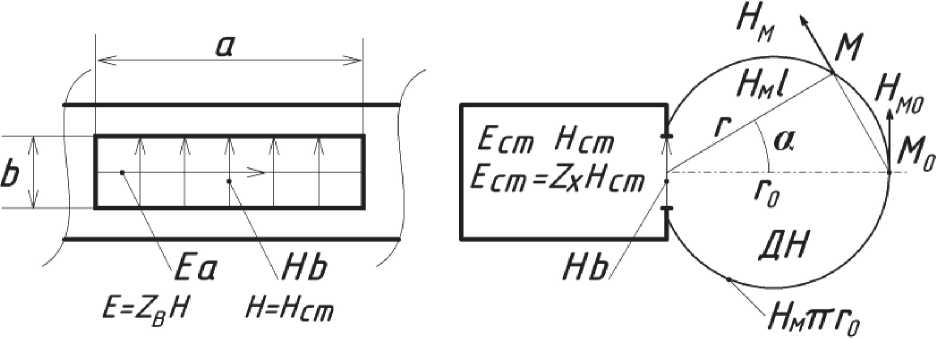
Рис. 1. Щелевая плоская антенна

Связь с полем в волноводе: H = E/Zв = Hст = Eст/Zх, откуда имеем E=Eст Zв/Zх, где Zх – характеристическое сопротивление поля в волноводе. 2.    ПРОВОДНЫЕ АНТЕННЫ ЦИЛИНДРИЧЕСКОЙ ФОРМЫ Рассмотрим далее антенны цилиндрической формы диаметром d и длиной образующей b (рис. 2, 3). Поверхность излучения – боковая поверхность цилиндра. Антенна может быть либо ёмкостью в виде двух параллельных пластин, либо индуктивностью (катушка), либо индуктивностью с сопротивлением (отрезок провода). На вход антенны поступает стороннее напряжение Uст, а ток I ст определяется в результате решения задачи. 2.1.    Антенна – ёмкость, рис 2, d, b<< λ (нерезонансная) Проводимость антенны Y = j ω C , сопротивление Z = 1/j ω C. С учётом равномерного распределения поля по поверхности антенны имеем следующие уравнения (внутренняя задача): Iизл= Hπd = j ω C Uст,              (9) U изл= Eb = – Iст / j ω C.           (10) Из уравнений (9),(10) имеем параметры поля на поверхности антенны: H = j ω C Uст/ πd, E = jIст / b ω C. Поделив уравнение (10) на (9) получим соотношение: Rизл = Uизл / Iизл = Iст / Uст ( ω C)2= Zвb/πd, откуда имеем: сторонний ток Iст = Rизл( ω C)2Uст и мощность

Так как потери не учитывались, имеем КПД=100% . Решение внешней задачи. Антенна для дальней зоны является элементарным вектором напряжения Uи зл с кольцевым током Iизл, и уравнения для поля в точке М на расстоянии r0 по нормали к центру антенны будут следующие: Hм2πr0 = Hπd, Eмπr0 = Eb. Определяя из этих уравнений Hм1= Hπd/2πr0 и Hм2= Hb/πr0 с учётом связей Eм = HмZв, E = HZв , и суммируя их, получим параметры поля в точке М на нормали к поверхности цилиндра: H м0 = H м1 + H м2 = H(πd + 2b)/2πr 0 , E м0 = Z в H м0 а затем с учётом равенства Hм0= Hм , соотношения r0= r/Cos α и фазового множителя определим и поле в пространстве: Нм = H(iid + 2b)cosa e-kr/2-nr , Eм = ZвHм, от угла φ поле не зависит. Диаграмма направленности антенны – поверхность тора. 2.2. Антенна – индуктивность, рис.3, диаметр d, длина b<< λ , для катушки в N витков имеем L = μπd2N2/ 4b , R <<  ω L. Сопротивление антенны Z = j ω L , проводимость Y =1/j ω L. C учётом равномерного распределения поля по поверхности антенны имеем следующие уравнения: Hb = U ст / j ω L = I изл , Eπd = – j ω L Iст = Uизл. Поделив второе уравнение на первое, получим сопротивление излучения: Rизл = ( ω L)2Iст/Uст= Zвπd/b, откуда имеем сторонний ток Iст = UстZвπd/b( ω L)2 , мощность излучения P = 05I U = 05I U .

излучения Pизл = 0,5 Rизл ( ω C)2Uст2 Ь

= 0,5I U .                изл , изл изл , ст ст . , ст ст.            КПД = 100% , так как потери не учитывались. \ !cm | ,Ucm / -^ " \ Vr/? / ^ XEb Hird Х-^М/ X           \ 4F--^        A \Vz        Hm2^ ^^^kv^  / Рис. 2. Антенна – ёмкость

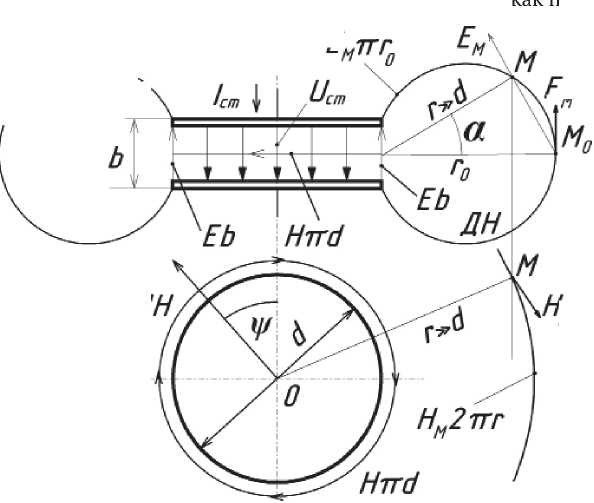
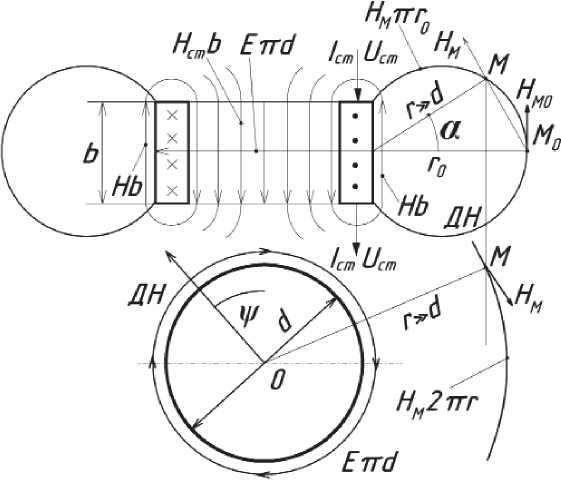
Рис. 3. Антенна – индуктивность

Решение внешней задачи. Для дальней зоны антенна – элементарный вектор тока I _изл с кольцевым напряжением U_изл и уравнения для точки М дальней зоны на расстоянии r₀ по нормали к центру антенны будут следующие:

Hмπr0= Hb, Eм2πr0= Eπd.

Из первого уравнения имеем Hм1 = Hb/πr0, из второго Hм2 = Hπd/2πr0. Суммируя эти значения, получим Hм0 = H(2b+πd)/2πr0, Eм0 = ZвHм0.

Поле в направлении α от нормали к центру антенны с учётом равенства H_м0= H_м , соотношения r₀ = r cos α и фазового множителя будет следующее:

Нм = H(2b + nd)Cosoc e~i^kr /2пг ;

E_м = Z_вH_м. От угла φ поле не зависит.

Диаграмма направленности антенны – поверхность тора.

• 2.3. Антенна – отрезок прямого провода диаметром d и длиной b , рис. 2, (пространство между пластинами заполнено металлом)

Для решения задачи определения поля этой антенны необходимо найти её комплексное сопротивление Z = R + j ω L . Активное сопротивление известно R = ℓ/ σ S, а индуктивность, даваемая в справочниках, получена из анализа всего магнитного поля (активного и реактивного), формирующегося при прохождении тока по проводу. Поэтому определим чистую индуктивность указанного отрезка провода. Для этого рассмотрим уравнение Фарадея (2а):

.(2а)

Из (2а) имеем XI_ст = ω μH_стS, или ω LI_ст = ω μH_стπd²/4. Учитывая, что магнитное поле в проводе кольцевое, имеем I_ст = H_стπd и индуктивность прямого провода L = μd/4 . Как следует из этой формулы чистая индуктивность прямого провода не зависит от его длины. Таким образом, имеем комплексные сопротивление и проводимость прямого провода :

Z = 1/G+ jX , Y = G(1 – jGX)/(1 + G²X²), где G = σ S/ℓ = σ πd²/4ℓ , X = ω μd/4.

Оценим безразмерную величину GX для конкретного случая:

d = 1мм , ℓ = 10 мм , f = 1Мгц , σ = 58МСм, μ = μ₀ = 0,4π мкГ/м.

В результате имеем: GX=58 ^. 10⁶π^{3 .} 10 ^{–9 .} 10^{6 .} 0,4 ^. 10 ^–6/8.10 ^–2= 8,98 > 1

Следовательно, единицей в формуле для проводимости можно пренебречь, и получаем Y = – 1/ X , то есть отрезок прямого провода на частотах 1 МГц и выше является индуктивной антенной. Эти результаты получены без учёта влияния проводов питания. Если учитывать провода питания, образующих одновитковую катушку, то такая антенна будет индуктивной антенной, рассмотренной в разделе 2.2.

Таким образом, можно сделать вывод, что все проводные антенны являются реактивными, то есть это либо ёмкости, либо индуктивности.

Итак, имеем для проводной антенны проводимость Y = 1/j ω L , сопротивление X = j ω L. С учётом равномерного распределения поля по поверхности имеем следующие уравнения (внутренняя задача):

I_изл =Hπd = U_ст/j ω L(11), U_изл = Eb = – I_стj ω L (12) и параметры поля на поверхности антенны H = U_ст/ j ω Lπd, E = – I_стj ω L/b, где L = μd/4

Поделив уравнение (12) на (11) получим со- противление излучения:

R_изл = U_изл/ I_изл = I_ст( ω L)²/U_ст= Z_вb/πd, откуда имеем:

сторонний ток I_ст = R_излU_ст/( ω L)² и мощность излучения P_изл = 0,5 R_излU² /( ω L)².

Решение внешней задачи такое же как и для ёмкостной антенны. В точке М имеем следующее поле Н_м = H(nd + 2b)cosae ^кг/2лг, E_м = Z_вH_м , от угла φ поле не зависит.

• 3. РЕЗОНАНСНЫЕ АНТЕННЫНА ОСНОВЕ ДВУХПРОВОДНЫХ ЛИНИЙ

Как известно, антенну на основе двухпроводной линии можно построить, выбрав определённую длину линии при холостом ходе или коротком замыкании на конце. При этом в линии вследствие резонанса образуется стоячая ТЭМ – волна с синфазным напряжением Uст и полем E,H, аналогичным полю в щелевой антенне. Напряжённость поля в щели таких антенн зависит от точности настройки на заданную частоту и теоретически может быть сколь угодно большой, так как реактивное сопротивление при резонансе стремится к нулю. Практически этого не происходит, так как начинает работать сопротивление излучения, и хорошим результатом считается E = Uст/b, где b ширина щели.

На рис.4 представлена двухпроводная антенна с коротким замыканием на концах – щель длиной a = λ /2 и шириной b< λ /2 в экране, питание подведено к центру щели. Распределение амплитуды поля по длине гармоническое E = E₀coskx. Напряжение и ток излучения находятся путём усреднения по длине щели U_изл=E_срb = 2U_ст/π, I_изл= H_срa = 2aU_ст/πbZ_в. ^р

Величина поля в щели таких антенн зависит от точности настроики на заданную частоту и при хорошей настройке можно получить в центре щели E0= Eст.

На рис. 5 представлена двухпроводная антенна, разомкнутая на концах, в микрополосковом исполнении длиной a = λ/2, шириной b < λ/4, толщиной h << λ, питание Uст подведено к центру одного из концов. Распределение амплитуды поля по длине антенны в результате резонанса – по закону синуса, поверхности излучения – две поверхности на концах с синфазным и практически равномерным напряжением и полем: Uизл = Eh = Uст , Iизл = Hb = Uстb/hZв, сопротивление излучения Rизл = Zвh/b.

Решение внешней задачи для этих антенн аналогично решению для щелевых антенн, раздел 1, рис. 1.

В заключение сформулируем основные положения и особенности предложенной методики, а также отличия её от известной:

За основу приняты уравнения Ампера и Фарадея в интегральной форме. В известной методике – уравнения Максвелла со сторонним током в дифференциальной форме.

Антенна является либо проводным устройством (двухполюсник или длинная линия), либо волноводным устройством. Она имеет объём, форму и поверхность излучения. В объёме действуют реальные сторонние силы – напряжение и ток генератора, а на поверхности излучения формируется свободное поле. В объёме антенны в соответствии с уравнениями интегрирование ведётся по линиям векторов и по площадям, а на поверхности излучения и в пространстве – только по линиям векторов. В известной методике антенна – объём пространства произвольной формы, заполненный некими сторонними автономными источниками в виде плотностей токов смещения (заряды в объёме антенны отсутствуют), которые для определения поля в пространстве интегрируются по объёму как заряды, причём форма антенны теряется.

Уравнения Ампера и Фарадея (как и уравнения Максвелла) связаны между собой волновым сопротивлением свободного поля, и эта связь используется в расчётах. В известной методике эта связь используется в конце расчётов, когда получен один из векторов поля в пространстве.

ВЫВОДЫ

Проведён анализ уравнений теории электромагнитного поля применительно к решению

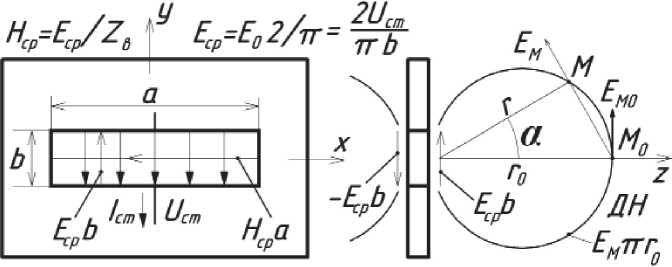
Рис. 4. Двухпроводная антенна с коротким замыканием на концах

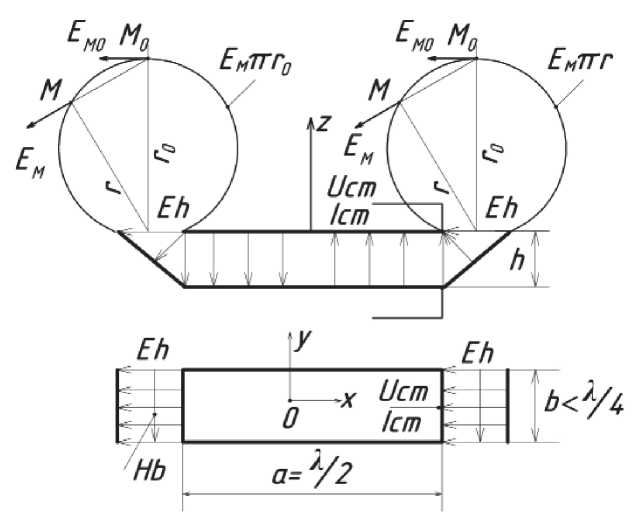
Рис. 5. Двухпроводная антенна, разомкнутая на концах

антенных задач. Показано, что уравнения Максвелла со сторонним током смещения для этих целей не пригодны.

Предложена методика расчёта антенн с использованием уравнений Ампера – Фарадея в два этапа: внутри объёма, занимаемого антенной, где действуют сторонние силы, и во внешнем пространстве с использованием теории элементарных антенн.

Представлены примеры расчёта ряда антенн по предложенной методике, доказывающие её работоспособность.