Методика расчёта вероятности попадания принимаемого сигнала в гауссовском канале в заданную область пространства

При приёме сигнала демодулятор должен принять решение о передаваемой сигнальной позиции. Наличие в канале связи шума приводит к тому, что принятая смесь сигнала и шума может оказаться в области решения другой сигнальной позиции, что приводит к ошибкам демодуляции.

Обычно шум считается гауссовским и на плоскости квадратурных компонент описывается гауссовской двумерной плотностью вероятности W(x,y) (рис. 1). Эта функция имеет нулевое математическое ожидание и некоторую дисперсию. В данном случае аргументами этой функции будут являться синфазная и квадратурная компоненты сигнала. Поверхность этого распределения изображается в виде «холма» с вершиной над точкой начала

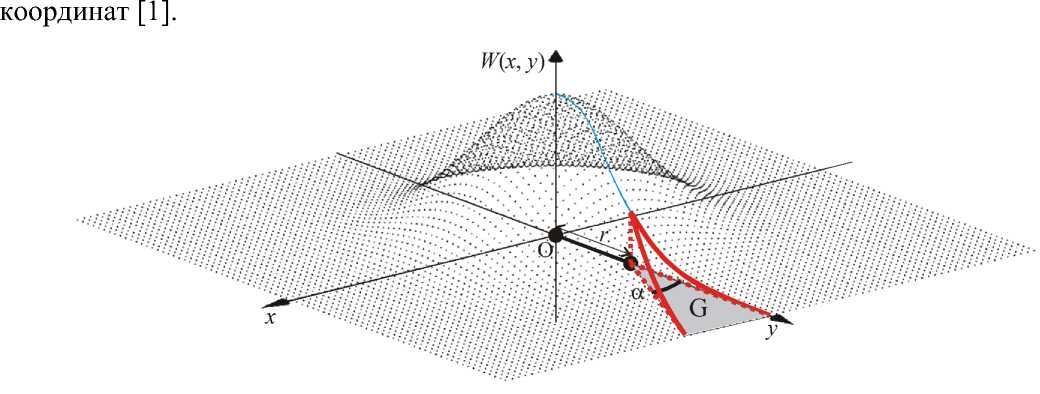
Рис. 1 Объём фигуры, вырезанной из гауссовского холма

Поскольку все сигналы передаются равновероятно, то на плоскости квадратурных компонент можно начертить границы принятия решений в пользу той или иной сигнальной позиции. Эти границы строятся путем проведения серединных перпендикуляров между соседними сигнальными позициями. Точки пересечения серединных перпендикуляров являются вершинами области принятия решения. В некоторых случаях крайние ребра линии границы уходят в бесконечность. Совокупность этих линий образуют диаграмму, известную как диаграмма Вороного[2] (рис 2).

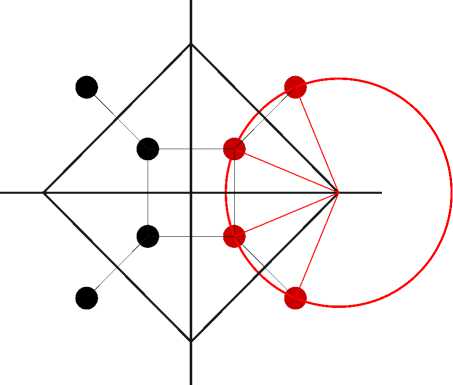
Рис. 2 Диаграмма Вороного

Центры описанных окружностей ближайших сигнальных позиций совпадают с вершинами диаграммы. На рис. 2 изображена одна такая окружность, от центра которой проведены радиусы к четырем сигнальным позициям.

С помощью представления областей принятия решения в виде диаграммы Вороного можно показать, как найти вероятность попадания принимаемого сигнала в любую область, ограниченную ломаной линией. Эта вероятность будет численно равна объёму фигуры, ограниченной сверху двумерной гауссовской плотностью вероятности, снизу – плоскостью квадратурных компонент и по бокам – плоскостями, перпендикулярными основанию, проходящими через рёбра ломаных линий области принятия решения.

Для нахождения объема подобных фигур можно выполнить двумерное интегрирование численным методом. Сложностью такого подхода является задание исходных данных и определение нижней и верхней оценки численного интегрирования. Другими словами, для разных расположений сигнальных позиций будут возникать новые объемные фигуры с новыми исходными данными, и нахождение помехоустойчивости для каждого из них будет являться новой задачей.

В работе используется другой метод решения этой задачи. Для этого вводится новую функцию двух аргументов Q(r,α). Эта функция будет описывать объём вырезанной фигуры из гауссовского холма, как показано на рис. 1.Назовём эту фигуру базовой. Эта фигура ограничена снизу – плоскостью квадратурных компонент, сверху – двумерной гауссовской поверхностью, а с боков – двумя плоскостями, перпендикулярными плоскости квадратурных компонент, образующими угол в противоположной стороне от точки О, а расстояние между этой точкой и точкой, где все три плоскости пересекаются, является параметром r.[3]