Методика распознавания объекта на основе кластерного анализа нечетких ситуаций

Процесс распознавания какого-то образа (объекта) предполагает определенную степень сложности представления соответствующей информации. Последнее определяется в значительной степени отсутствием полной совокупности све- дений. Эта информация в лучшем случае может носить стохастический характер. В других случаях будет носить более неопределенный нечеткий характер, который можно представить в количественном виде элементами нечетких множеств [1, 2] нечеткой алгебры [3]. Элементы такой алгебры предполагают, в свою очередь, использование специальных методов шкалирования и измерения [4]. При этом должны учитываться принципы нечеткой логики [5-7].

Постановка задачи

Измерение нечеткой информации согласно [4] основано на использовании условных шкал нечетких эталонных объектов – термов на базовом множестве, путем назначения (выбора) типовых представителей. В последующем фаззифициру-ются все значения базового множества, характеризующие параметры объекта, путем использования функций принадлежности. На основе условных шкал представляется неполная нечеткая информация путем определения её нечеткого включения в типовые термы.

Решение задачи

При этом терм с наибольшим включением текущей ситуации можно считать предварительным результатом измерения нечеткой информации. В этот результат вводятся поправки с использованием дефаззификации при использовании функций принадлежности всех термов конкретной шкалы.

В связи с тем, что объект является достаточно сложным, для его описания целесообразно использовать такие понятия, как нечеткая ситуация [2-8]. Ее параметры – результат рассмотренных измерений. Поэтому с учетом этих данных, полученных на предметных шкалах, нечеткую ситуацию ^^^ ) на момент времени t можем представить следующей совокупностью данных:

St ={ A;,^⁰)/^ (1)

где ?е{1,2,...,/} – номера признаков (параметров) объектов; 7,e{0,l,..V,} – номера термов на условной шкале, соответствующей i -му параметру объек та; // (л^Х1) – функция принадлежности значения x_t нечеткому множеству – терму Ji •

Обобщенное идентифицированное выражение функции принадлежности согласно [3] представляется в виде:

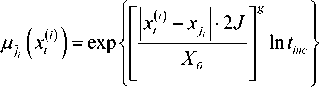
где х_б – базовое множество на предметной шкале; g – параметр, характеризующий нарушение комплементарности нечетких множеств (термов) условной шкалы.

Для того чтобы распознать образ объекта, необходимо сравнить текущую нечеткую ситуацию, характеризующую объект, с типовой нечеткой ситуацией. Сравнение возможно в виде нечеткого включения:

или равенства

где выражает оператор импликации следует учитывать его особенности [4, 9].

В выражениях (2) и (3) символ t можно принять за обозначение текущей ситуации, а g – типовой.

Типовую ситуацию по аналогии с (1) можем представить так:

^Tf I ^7, (^XV)/^xy?} ’       (5)

Каждый элемент ситуации (1) и (4) характеризуется значением параметра и соответствующей функцией принадлежности.

Если ввести виртуальный эталон объекта, то можно перейти с предметных шкал на универсальные шкалы, на которых базовые множества «6 =1- Переход на универсальные шкалы осуществляется с использованием функций отображения [3, 4]. При этом выражение (2) перепишется в виде:

^Д«р)) = ехрН |a,w-«('^j] -InZ^J , (6)

Заключение

Приведенные выражения ситуаций (типовых) позволяют все возможные состояния изучаемого (наблюдаемого) объекта представить матрицей кластеров (л^^*'*)) [4, 10], что не снижает общности последующих исследований. Её вид в единицах универсальных шкал (^a*) примет вид рис. 1. В матрице («/'') на рис. 1 выражены элементы через параметры типовых ситуаций в единицах универсальных шкал. Выделено 7 кластеров по принципу суммирования индексов (номеров) термов (Ji) • Суммы равны, соответственно, 0, 1, 2, 3, 4, 5, 6. Подобный подход условно предполагает, что с ростом суммы номеров кластеров возрастает степень опасного состояния, т.е. так выражаются Spur движения текущей ситуации во времени St с параметрами (^zO ' Spur, так определенный след ситуации, позволяет наметить ответные меры со стороны оператора охраны. Более конкретные выводы потребуют достаточно объемного экспе- римента, например, численного. Методологию данного эксперимента можно найти в [3]. При этом следует учитывать особенности ситуации [11, 12].

Л/(л')=

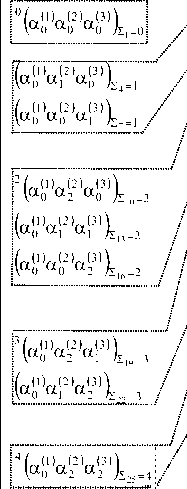
ДаИа^а®^^, H^'M^J (а^а^ар^-,]

>(арРхр>ар^||=3 (а^а!2^!3^^., (а^арЦ3^^

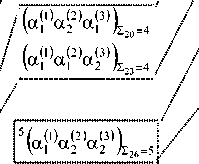
Ф^«Р’аР’)1|2=4

H’aPM3’!,^ Н’аРМЧ,^

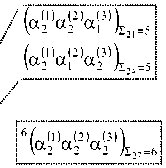
■•■•'■ (а^ар’ар1)^^ (а^ар^ар^^з НМ^М3')^

Рисунок 2. Матричное и кластерное представление типовых ситуаций