Методика решения задачи поиска частотного отклика сборной конструкции трубопровода с применением метода конечных элементов

 outputs and inputs of different notation business processes]. Available at:    nection_inputs_outputs/connection_different_notations (accessed 18.02.2014).

12. Svyazyvanie protsessov dlya peredachi upravleniya [Business processes linking for management transfer]. Available at: php/ru/csdesign/bpmodeling/connection_processes/connec tion_transfer_control (accessed 18.02.2014).

Изделия авиационной техники сегодня представляют собой сложнейший комплекс систем и оборудования, интегрированный в планер. В полете все элементы современного самолёта должны работать как одно целое, обеспечивая соответствие заявленным при его проектировании характеристикам. Однако учёт совместной работы элементов систем и планера при различных вариантах совместного нагружения является сложнейшей задачей, которая решается с применением итерационных подходов, с неоднократными доработками и модификациями тех или иных элементов и согласованием целого ряда параметров.

Трубопровод - сложнонагруженная конструкция, исследование работы которой - комплексная задача, существующая на стыке исследования экспериментальных данных натурных испытаний, результатов традиционных численных решений и высокопроизводительных численных решений (рис. 1).

Традиционные методы, описанные в [1-5], являются громоздкими и сложноприменимыми в производстве. Аналитические же методы в большей степе -ни позволяют рассматривать отдельные элементы сборных конструкций и представляют известную сложность, связанную с определением всех возмож- ных типов нагрузок и действующих напряжений, что не позволяет рассматривать масштабные сборные конструкции, где велико взаимовлияние элементов друг на друга, особенно при динамическом нагружении. Экспериментальные же исследования представляются слишком дорогостоящими ввиду необходимости наличия соответствующего оборудования и программных средств для обработки потока данных эксперимента (например, при тензометрировании динамических испытаний) и используются в основном для подтверждения заявленных характеристик и при отработках конструкций. Численные же методы решения подобных задач представлены системами инженерного анализа, основанными на методе конечных элементов.

Методы численного решения задачи определения динамического напряженно-деформированного состояния трубопроводных систем описаны в серии работ [6-15].

Основные тенденции развития методики [6] заключаются в более глубокой проработке и уточнении средств рассмотрения экспериментальных данных натурных испытаний, а также в более точном определении параметров надёжности системы через сравнение частот отклика и возбуждения сборных конструкций.

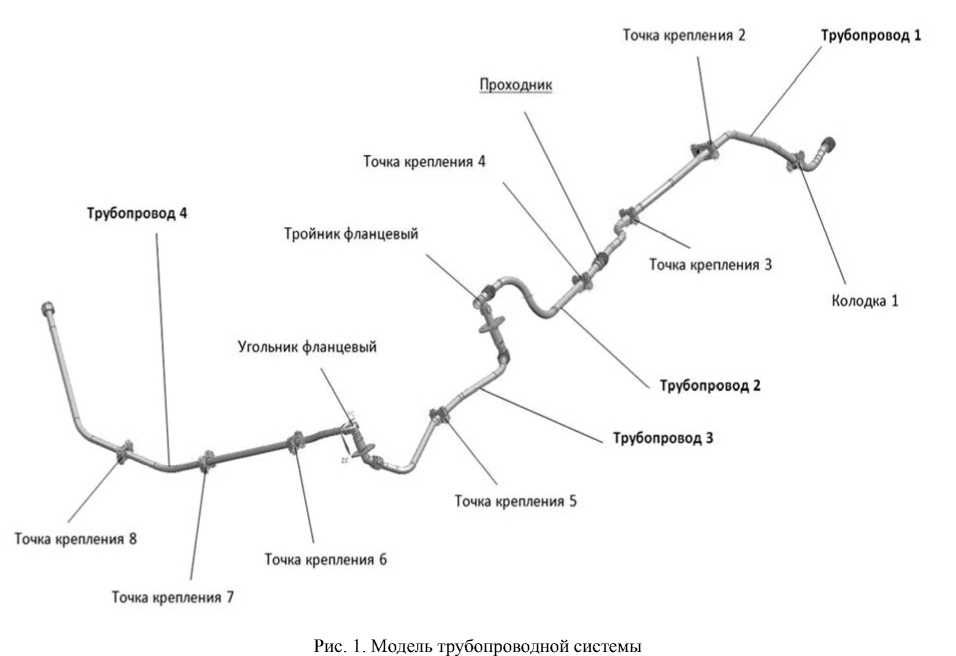
Согласно методике [8], необходимо рассмотреть задачу определения частотного отклика конструкции трубопроводной системы для определения критических частот работы трубопровода. По результатам работы необходимо сравнить критические частоты с рабочими частотами системы и устранить совпадающие частоты путём изменения конфигурации модели трубопровода или точек его крепления к элементам каркаса планера. Однако обнаружено, что при анализе конечно-элементной модели сборной конструкции трубопровода по заданному диапазону частот (анализ Transient static) в системе инженерного анализа ANSYS возможно разрушение контактов модели, что обусловлено нелинейным увеличением энергии колебаний постоянной амплитуды с увеличением их частоты. Таким образом, необходимо определить функцию колебаний точек крепления трубопроводов, позволяющую исследовать вибрации трубопровода с постоянной энергией и переменной частотой.

Выполнен поиск функции перемещений в виде f (t) = А( t) x sin ю( t);                  (1)

где t – время, с; A ( t ) – закон изменения амплитуды колебаний по времени; ω( t ) – закон изменения частоты действия внешней силы.

При этом амплитуда функции (1) уменьшается со временем, а частота возрастает.

Модель сборной конструкции, подвергаемая динамическому анализу, может быть рассчитана при условии сохранения целостности контактов во время действия любых возникающих в процессе приложения исходной нагрузки сил. Опытным путём установлено, что максимальные амплитуды колебаний системы не вызывают нарушения контактных связей при амплитуде колебаний, равной 2 мм.

Эффекта разрушения контактов в модели сборной конструкции можно избежать путём применения закона постоянства энергии колебательной системы при автоколебаниях:

22 m x ю x A -----------= const, 2

где m – масса системы, кг; ω – частота колебаний системы; A – амплитуда колебаний системы.

В любой момент времени t m x ю0 x A = m хю2(t) x A2(t)

2        =           2         ^{.             (} )

Таким образом, амплитуда зависит от частотного диапазона исследования:

A ( t ) = ^,            (3)

to ( t )

где ω₀ – начальное значение частоты (условно принятое равным 1); А 0 – условное начальное значение амплитуды колебаний конструкции, не приводящее к разрушению контактов в модели.

Частота по условиям задачи поиска частотного отклика зависит от времени по линейному закону ю = k ■ x + b .                     (4)

Раскрывая уравнение (3) с учетом (4), подставляя граничные условия, получаем

A ( t ) = у ,                     (5)

где K – коэффициент пропорциональности, зависящий от принятых начальных значений амплитуды, частоты и шага по времени.

Для рассматриваемого расчётного случая значение К = 0,109 соответствует оптимальным с точки зрения задания переменных нагрузок в конечно-элементной модели трубопровода значениям начального времени t 0 и начального значения амплитуды ω( t 0 ) (исходные параметры для этих значений: t 0 = 0,1 с, A 0 = 2 мм).

Из условия известных значений начальной и конечной частот вращения авиадвигателя как источника возбуждения колебаний n(t1) → 0 и n(t2) = 700 об/мин, получено:

ю ( t ) =---- x t x 2 xn .

Согласно приведенной методике, функция (1) с учетом вышеуказанных условий имеет вид (рис. 2)

0,109 x sin(73,303 x t) f (t) =  ------—------ t

Рис. 2. График функции f ( t ) с постоянной энергией колебаний в системе при увеличении частоты с заданными параметрами частотно-временных характеристик

Функция (7) позволяет задавать перемещения точек опор трубопровода, анализировать сборные конструкции при постоянном значении энергии систем без разрушения её контактных взаимодействий и применима для инженерных анализов в стандартных КЭ-пакетах.

Частотный отклик, полученный в результате анализа модели по представленной методике, отображен на рис. 3.

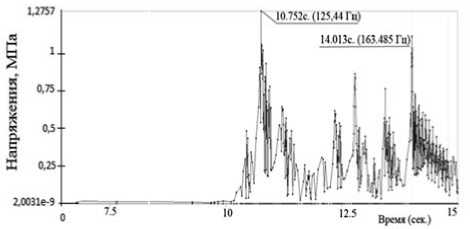
Рис. 3. Частотный отклик модели трубопровода до модернизации

Таким образом, однозначно определён первый резонансный пик всей конструкции при частоте 125,44 Гц, что находится в диапазоне рабочих частот. Следовательно, модернизацию необходимо выполнить таким образом, чтобы исключить возможность появления резонансных пиков в диапазоне рабочих частот.

Выполненный анализ частотных откликов модели с модернизированными кронштейнами подтвердил способность конструкции эффективно демпфировать динамические колебания. Отсутствие ярко выраженных пиков динамических напряжений и снижение общего фона напряжений при колебаниях системы с частотой, при которой в исходной конструкции прослеживались ярко выраженные пики напряжений, наглядно представлены на рис. 4.

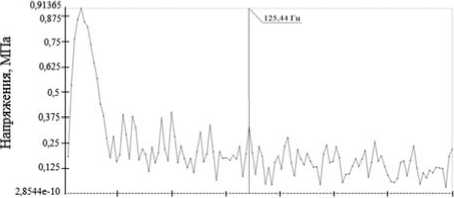
О 0.125       0.25 МИ М 0.625       0.75         0.9

Время (сек.)

Рис. 4. Частотный отклик модели после модернизации

Таким образом, уточнена методика определения частотного отклика протяженных сборных конструкций.

Применение описанной методики позволит избежать итеративного поиска зависимости возбуждающей силы от времени и впоследствии эффективнее определять параметры любых решателей в стандартных КЭ-пакетах, применяемых для динамического анализа протяженных сборных конструкций с применением нелинейной контактной задачи теории конечных элементов.