Методика решения задачи стохастической оптимизации технологических процессов обработки металлов при стохастическом распределении начальных условий

При выборе оптимальных параметров различных технологических процессов чаще всего приходится решать задачу в условиях неопределенности. Неопределенность понимается в том смысле, что параметры рассматриваемой системы имеют вероятностный,случайным характер.

Пусть <<),! ,! > - исходное вероятностное пространство; здесь ci-множество событий, на которых определена вероятность i . Считается, что класс событий к образует алгебру событий, т.е. содержит достоверное событие (множество О) и невозможное событие (множество О) [ 1 ]- - Пусть даны некоторые случайные Функции f' (х(9),9), где tsIR ,6^1,vG0,m. Значения вектор - функции х(9) зависят только от наблюдаемых событий г . т.е. считается, что х(в) - измеримая Функция относительно г . В качестве критерия оптимизации (целевой Функции) рассмотрим Функционал В°<х(9)} :

р°{х"(9 )}=jf° (1Г(е ),е )p(dS )^Mforx(e >,е ) . (1)

Теперь общая постановка задачи стохастической оптимизации Формулируется как задача поиска I -измеримой вектор-Функции

х(9), минимизирующей функционал СО при ограничениях вида:

? Чтсея^/ (z(9),e)p«ie 1=м? (х(е ),e)

для Р-почти всех Q.

х(в )еХ(в),

где X(6)~ некоторое множество n-мерного пространства 0?,М-математическое ожидание некоторой случайной величины

Постановка задачи <О-<3> напоминает задачу нелинейного программирования. Отличия от последней состоят в следующем:

• 1)    сложность вычисления Функционалов у¹ (z(9 ) >,i=rO,m ; Формально это сводится к вычислению интервала по мере Р которая часто даже не задается в явном виде;

• 2)    Функционалы У*{т(<9 )>,1^0ла часто оказываются негладкими Сне имеют непрерывных производных).

Для примера рассмотрим постановку задачи стохастической оптимизации при выборе режимов настройки роликоправильных машин (вертикальных перемещений роликов) для правки длинномерных щ>о Филей. Постановка и методика решения задачи правки рассмотрены в работе f2J.

Элементарное событие в -это процесс правки при Фиксированных значениях всех исходных параметров. Назовем событием а подмножество О , которое представляет совокупность процессов правки при значениях случайных исходных характеристик из некочороп заданного интервала. В частности, считается, что случаиишчи параметрами процесса являются предел текучести материала о и я начальная искривленность профиля я . Тогда совокупность пр» нот-сов правки при х б[х*,х^* еГс^,^ ' ' ) составляют подмноже: г-

О О О     8   8  3

во Д, а семейство подмножеств Д определит F . P-это вероятно»-!-события Д.

Вектор управления х(9) представляет настройку роликоправильной машины, f°(z(9),в)  - модули конечной искривленности профиля. К ограничениям (2) следует отнести уравнения, описывающие процесс знакопеременного изгиба, ограничения на параметры управления, по прочности и т.д.

Рассматривается класс задач стохастической оптимизации, г которых стохастическими являются только начальные условия. В этом случае, если плотность распределения решения удастся oik*- нить через плотность распределения начальных условий, задача стохастической оптимизации сведется к задаче нелинейного программирования, решение которой может быть найдено достаточно просто [3].

Рассмотрим методику вычисления целевой функции (при необходимости и ограничений) при независимых начальных условиях.

Согласно определению интеграла по вероятностной мере

Р°(х'(е )).Нт

П-*00

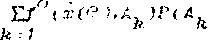
где А - рведенн ы ь» вышг непе*р^секающие< м подмножества U;

f (х(в).Д), (А^-Д)               случайной Функции f (х(в)»6),

'          к к

т.е. /^ (х(в ЬА^ )игедсч^шучкхг собой последовательность простых Функций, сходящуюся к /°(х(в)>в) ,

Если предположить, что появление определенных значении на чальных параметров а>Ъ>-рС - независимые события, тогда ве роятность Р<Л > появления события 2

к                     к

дение соответствующих вероятностей V

определяетс я

как

произвел

а , b

С J

с

I

Г* Г"’ 1 f3J

Теперь соотношение (4) можно переписать в виде :

п т    г  ,

/Тх^М^Е Е- . . T^tsteu     . _Р^С (6)

• 1.1    J=1   1=1

Р®=Р(аеДа, )><-f.n; с V°^-1;

• 1             {1

.                   m р“=1(Ь€ДЬ^)^=1,1г: T !j=’;<

1°=Р(сеДс )Л = 1,п; 52 1^С=/.

1           11=1

Приближенное значение целевой Функции может быть определено согласно соотношению :

F°          (Tie ))=Lim Е Е- • • ^(xiei.A )VЛ ^Ь Р^С (в)

n'mv              1 = 1 j=i 1 = 1          k 1 j 1

Для построения p°       (x(9)> прежде всего необходимо n.m....т ус гановить

зависимость

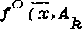
) от вектгзг'а управления х(в)

при

определенных фиксированных значениях а.,Ь, ,с <в большинстве практически важных задач явное выражение таких Функций отсутствует). Воспользуемся методом математического планирования второго порядка [4], позволяющим по “экспериментальным точкам" (имеется в виду численный эксперимент) с помощью метода наименьших квадратов построить интерполяционную модель второго порядка Функции цели /°(х>А^) . Математическое планирование ■жслеримента позволяет построить модель вида [4] ".

f° (х,А. )=(3 +3 ж х +. . . *0 х х +. . . +/?       .       (9)

"Экспериментальный точки" получены из решения соответствую щей задачи при заданном векторе управления х(6) и фиксированных параметрах cub,-.,с- Для определения неизвестных коэффициентов

(3 Ср=О,т) может быть использован композиционный центральный план. С учетом <9) целевую Функцию <8) можно выразить в виде :

Cm,.. V^o^t^a³^-- ' ^Vi^J^ ■ '^в ’ ⁽¹⁰⁾

где коэффициенты у (р=О>т) определяются значениями (3 (р=О>т) и видом функционала <8>.

■Хнзлог лчным образом может быть определен детерминированный аналог ограничений.

Таким образом, в случае независимых начальных условий задача стохастического программирования свелась к задаче нелинейного программирования, для решения которой можно использовать, например, метод деформируемого многогранника в соче^анчи с мь - ТОДОМ штрафных функций [31-

бить интервалы изменения <у   и х„ в О

профиля <. х^э случайными

на подинтервалы

где

где

ра з-

, min rT, ... j

6     8      , S

, min

’*0 '

ши t t ^xo ^№o

,a^*^ )> Дм -[н^,м^^{+ }} >, тогда <8) примет вид : S   ООО

Да - [o^ S 3

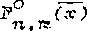
n m

Z Z / (х. А, ^ = ь =г ,

^pj^=F ^ ^sA3 i*;

in

P^PCcx ^Acr^ ), l=1,n; 5Z P^l .

Следует отметить, что в данном случае нет необходимости в определении детерминированного аналога ограничений, так как ограничения в виде равенств рредставляют собой уравнения, описывающие поведение материала в процессе правки,и уже использовались при получении соотношения СЮ). Ограничения в виде неравенств наложены на параметры вектора управления и являются в данной задаче детерминированными.

В случае зависимых начальных условий нарушается условие <5). Все дальнейшие предпосылки остаются справедливыми. При этом возникает задача оценки плотности распределения решения через плотность распределения начальных параметров.

Если случайным является только одно начальное условие, то плотность распределения решения можно оценить с помощью следующей леммы f5J.

Лемма: Если имеется случайная величина ? ,а y-f(x) - непре рывно- дифференцируемая функция С /' Ст )^) ; п=7(? )  >, то плот ности Р^Сш? и v^(y)

связаны след/юшеи Формулой :

Р^Су?^ ’(У>)-(/ (У))

Если начальных параметров, распределенных стохастически, несколько, то можно предложить следующий путь решения задачи.

Пусть "^(^ ^^2'" "'^г ^случайная величина в   IRn(совокупность зависимых начальных условий); у= (т;,>"П_,-. . .г, )          -решение, которое представляет собой случайную величину в В< с распределением вероятностей, которые однозначно определяются распределением величины”^ : 1 V- (х ,. . .,$ )йя= 3   ^"(у4>...»у )dy=1,

<   7        п                   7       Ж

Rn               RW причем :

7?i=/| (5 ^ - • • ^п^ 1=1^» - «^^ •                      (13>

Произведя замену переменных, выразим

F_? (х^..., х^):

^п^У'’^ через

где 1= ---!-----— =det

Г^<

-якобиан обратного преобра-

acrj ,.. .,т) ) 1 го

^{L а}^ъ ^J JR

зования.

Осталось определить

,х ) ~ вероятность

появления определенного комплекса начальных условий

совместного

. В завися-

мости от вида распределения плотность распределения определяет- сн по-разному. Так, в случае n-мерного нормального распределения согласно [6] получим :

п

° е.трГ -0,5°

S £=1

^Л,_ьбя JA 5

-$ р*1 ^ь^к^^

^У^Р^к1

где

KJh"XM

j=h (дисперсия),'

coiHi .

; }, ./^(ковариация)

,j,k=1,n.

• f.    Приведена постановка и дан возможный вариант методики решения задачи стохастической оптимизации технологических процессов обработки металпсз при стохастическом распределении зависимых и независимых начальных условий.

• 2-    Рассматривается постановка и методика решения задачи стохастической оптимизации на примере выбора рациональных режимов правки длинномерных профилей.