Методика синтеза критериев оценки состояния газотурбинных двигателей

В настоящее время формирование критериев определения технического состояния газотурбинного двигателя (ГТД) является процессом, основанным на опыте и знаниях целых исследовательских коллективов, во многих случаях требующим индивидуального подхода и высокой квалификации научных и инженерных кадров.

В связи с этим появляется необходимость создания формализованной методики синтеза критериев контроля и прогнозирования технического состояния (ТС) авиационных ГТД. В данной статье автор рассматривает разработанную методику, используя семантику теории множеств и теории образов в связи с тем, что с их позиций возможно описывать объекты любой сложности и природы.

Согласно терминологии [1] полностью и всесторонне описанный любой объект называется образом. На практике осуществимо описание образа только идеального объекта, которое используется для установления аналитических связей между его параметрами. Потенциально возможное описание реального объекта есть его изображение.

Любое изображение объекта в общем виде представляет собой трёхкомпонентную систему [2]:

g = (m,t,dm\ "

где Af – множество, характеризующее пространственную структуру объекта – архитектонику; T – хроноструктура, то есть структура изменения параметров архитектоники во времени; D^ – диапазон допустимых изменений параметров архитектоники; при выходе хотя бы одного параметра за этот диапазон объект перестаёт быть самим собой.

В общем виде M = [тПрТПг, ...,т_пм), где m₍ – подмножество параметров, непроизводного в рамках данной задачи i -того элемента объекта:

m, = foi^pj,

где i9e – подмножество параметров, характеризующих геометрию элемента; ^i – подмножество параметров, характеризующих расположение элемента по отношению к остальным элементам; Pi – подмножество параметров, характеризующих природу элемента.

В общем виде хроноструктуру можно представить как функцию

T(M,t), где t – время. Изменение архитектоники во времени обусловлено воздействием на неё “внешней средой”. В данном контексте под “внешней средой” понимается совокупность всех воздействий на объект из вне, включая воздействия субъекта.

Также хроноструктуру можно представить множеством, если в ней отражено изменение па- раметров дискретно:

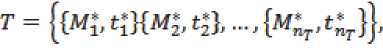
Диапазон допустимых изменений парамет- ров архитектоники представим множеством

^m "~ |^mp ^мг» ■■•• ^n_DM j'

где^MV^MZ» —'^n  – подмножества диапазо нов допустимых изменений параметров:

^Mi ⁼ {^М^'^ЛТкР^Мри'

где                        1 , d-Mki —                  ]^,

771171 l7HCLYJ              L ‘ПИП l77UbrJ dMpi — [timin'^*ma*l .

Вышеописанное представление изображение объекта трёхкомпонентной структурой G = M> будем называть первичным, так как все остальные параметры объекта являются производными от его архитектоники.

Множество технических состояний объекта G = (M,T,D_M> есть множество первичных представлений c — (c_v c₂, ...,c_ncj, где C_i = (M_£,T_i,D_2lf.). Причём

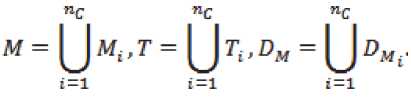
Для субъекта не всегда необходимо полное описание объекта, и представляет интерес лишь его часть; а осуществить первичное описание в большинстве случаев либо не представляется возможным, либо не рационально. Поэтому решение некоторых задач, включая задачи технической диагностики, сводиться к описанию некоторого аспекта изображения объекта – конфигурации, как правило, параметрами производными от ар- хитектоники.

Для определения технического состояния, в котором находится объект, необходимо оценить объект по результату его работы – эффекту. Из-за того, что объект не может существовать без «внешней среды», и исключить её влияние на объект невозможно, следовательно, субъект познаёт (или оценивает) объект исходя из результатов его взаимодействия с «внешней средой», иными словами на основании эффекта системы объект-«внешняя среда».

Ее = [pe1'Pe2' — 'Psnp£); критерии эффекта множеством D^

'£2

[ , каждый

элемент множества ^E выглядит следующим образом:

"PE

^Е1^: /\(Pei ⁶      . ;d_Ei 1) ^ E* = Ej,

hl / yv“J L cijmtn' “Чтах^'           1

>=1

где E – эффект системы объект -”внешняя среда”.

Если M – область значений M , ^ – область значений N ; то область значений i -того параметра эффекта Реё является образом (не путать с образом в [1]) декартова произведения множеств M и^, полученным по закону :

fMxN; MXN ^>pEi или

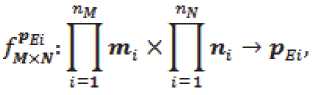
где m_t и n^ – области значений 771, и 77g соответственно.

Если множества S' иc сформированы таким образом, что одно является биективным отображением другого, то есть существует закон fs ■ E *-* C , то справедливо:

E* = E^C* = Ct, где C4" – ТС, в котором находится объект.

Следовательно, в данном случае параметры эффекта являются первичными параметрами ТС.

Использовать первичные параметры ТС не всегда рационально, поэтому, как правило, используют вторичные (диагностические) параметры, измерение которых целесообразно.

Оформим диагностические параметры мно-жествомp ={PvP2— Pnp}, диагностические признаки множеством S — {SpS2' •■•'■SnsJ, критерии ТС множеством ^c ~ {^cp ^сг> ••■ > ^cnDc ] , каждый элемент множества ^c выглядит следующим образом:

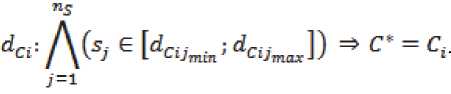
Если Pi – область значений Pi ; то Pi является образом декартова произведения множеств Р^Ё , полученным по закону :

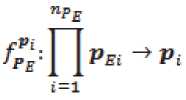
Если S^ – область значений Sj ; то s^ является образом декартова произведения множеств Pi , полученным по закону :

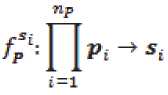
Если определить аналитически отображения fPEi fPi f^si

JmxN’ JPE'JP затруднительно, как в случае сложного многоэлементного объекта диагностики – ГТД, то диагностические признаки целесообразно сформировать эмпирически.

Рассмотрим такой способ определения диагностических признаков для некоторого ТС ГТД c* .

Параметры «внешней среды», которые субъект контролирует, формируют множество X = {xp^,...,^}; параметры «внешней среды» неконтролируемых воздействий обозначим Z = {z_pz₂,...,z„_z}; параметры эффекта обозначим ^Y = {УрУг У_пу]^.

Таким образом, зная параметры “внешней среды” и эффекта, можно сформировать множе-ствоД = {X,Y,Z} , описывающее состояние ГТД. Такое множество назовём характеристическое. Как правило, непосредственно данное субъекту характеристическое множество представляет для него набор разрозненных величин, и пригодно для решения задач диагностики только после ряда преобразований.

Если на все экземпляры ГТД подавать одни и те же (стандартные) воздействия, или на основании полученных откликов при различных воздействиях определять те отклики, которые бы возникли при стандартных воздействиях, то характеристическое множество A = {X,Y,Z] преобразуется в множество вида ^А= = [Ус1^Ус2 Успу}, где Ус1'Ус2' "чУспу – параметры эффекта при стандартной «внешней среде». Полученное множество ^г назовём приведённым характеристическим множеством.

В качестве характеристик ГТД могут выступать дроссельные характеристики регистрируемых за один полёт параметров, приведённых к стандартным условиям. Одной из форм представления дроссельной характеристики каждого i -того параметра может быть множество ^Bi = {^lAz ⁶in_BJ , где ЬЦ, Ь^,.:,^^. – коэффициенты полинома степени Tig , которым описывается дроссельная характеристика. Таким образом, приведённое характеристическое множество ГТД имеет следующий вид:

A= = [S^.-Smb при условии, что в полёте регистрировалось m + 1 параметров ГТД: для m параметров строятся дроссельные характеристики, а один параметр используется в качестве режимного.

Если b" область значений параметра ^ij , то графически ТС ГТД, оформленное характеристическим множеством, можно отобразить точкой ^AXbiv ^12' —’Ьц,...,Ь_тпв^) в метрическом пространстве, образованном декартовым произведением множеств:

-ПЖ- i=l j=l

с метрикой в. В случае неточного определения элементов ^ij – можно отобразить областью в этом пространстве. Меру различия между техническими состояниями соответствующими одному и тому же двигателю, но в разные полёты будем определять метрикой:

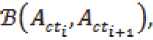
где ^Act_t – приведённое характеристическое множество ГТД, соответствующему полёту, начавшемуся в момент времени tg , ^^5ti+i – приведённое характеристическое множество ГТД, соответствующему полёту, начавшемуся в момент времени ^"i +1; причём разница (^41 ^£i) складывается из времени работы двигателя.

Зная скорость изменения конфигурации

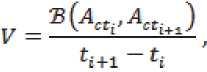
можно определить конфигурацию в будущий момент времени, т.е. решить задачу прогнозирования параметров работы ГТД.

Выберем в качестве признака ТС c метрику ®(^_D^J, где ^^^D – приведённое характеристическое множество ГТД на момент времени £q , соответствующий началу эксплуатации ГТД или после его капитального ремонта; ^Act – приведённое характеристическое множество ГТД на момент времени t , при котором конфигурация ГТД отвечает признакам объектов данного класса технических состояний.

Для определения метрики эмпирическим способом сформируем контрольную и экспериментальную группу экземпляров ГТД. Контрольная группа состоит из двигателей, которые за ряд полётов не достигли ТС c . В экспериментальной наоборот, все двигатели за ряд полётов достигли технического состояния c . В результате для каждого ГТД в экспериментальной группе будет справедливо неравенство ^B3mi-n — ® (^ct₀'-^ct) — ^B3max , а для каждого ГТД из контрольной группы – ^BKmin — ®(^ct_D'^rt) — ^Kmax ^.

Если промежутки [^3min-' ^B3 mcjrl и t^JCmin ' ^BK maxi не пересекаются, то метрика ®(^_D^J приемлема в качестве диагностического признака состояния c . В случае если промежутки пересекаются необходимо задать другую метрику пространства IB, так как при попадание значения признака в область пересечения однозначно определить ТС ГТД будет невозможно.

Условие оптимального диагностического признака следующее:

^^BK ^e timin' ⁵Amax] ^A ^83 E [S3_min,⁵3ma^l'

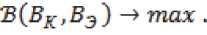
Для реализации описанной выше методики на данный момент в программной среде Labview разработано приложение, которое реализует следующие функции:

• .    считывание данных из полётных файлов;

• .    усреднение значений параметров на указанном промежутке времени;

• .    устранение выбросов значений параметров;

• .    приведение значений параметров к стандартным атмосферным условиям;

• .    построение дроссельных характеристик параметров.

Планируется доработать приложение таким образом, чтобы в нём на основании данных наблюдения происходило вычисление метрики-признака технического состояния.

Вывод. В статье представлена модель описа- ния технического состояния ГТД с применением теории множеств, описан алгоритм выбора диагностических признаков. Приведены разработанные автором средства реализации описанной методики.