Методика синтеза одномерно сканирующих антенн на основе модулированных метаповерхностей

В последние годы наблюдается устойчивый интерес к электромагнитным метаматериалам и метаповерхностям, в том числе как к возможной основе для следующего поколения планарных антенных устройств различных частотных диапазонов – от СВЧ до оптического [1, 2]. В частности, в СВЧ-диапазоне решения на основе метаповерхностей характеризуются возможностью гибко управлять электромагнитным полем, дешевизной и технологичностью в изготовлении [3–6].

Метаматериалы – это макроскопические композитные материалы периодической или непериодической структуры, которые благодаря искусственно созданным включениям или неоднородностям в основной среде либо имитируют свойства известных материалов, либо приобретают такие физически реализуемые свойства, которые не возникают или недоступны в природе. Включения обычно имеют масштаб меньший, чем длины волн, на которые они влияют. Форма, геометрия, размер, ориентация и расположение таких включений задают матери-– 751 – алу необходимые свойства, например, блокируя, поглощая, усиливая или преломляя электромагнитные волны.

Метаповерхности можно считать двумерными метаматериалами. Преимущество метаповерхностей заключается в том, что они занимают меньше физического пространства, чем полноценные трехмерные метаматериальные структуры, более технологичны в производстве, а также в большинстве случаев обладают меньшими потерями.

На основе метаповерхностей могут быть реализованы периодические замедляющие структуры поверхностных волн, где фазовая скорость одной или нескольких обратных пространственных гармоник, возникающих из-за периодичности структуры, превышает скорость света. В таком случае излучение, которое образует так называемую вытекающую волну, может быть использовано для создания антенн [5–8]. Более подробно физический принцип работы антенн вытекающей волны на основе периодически модулированных метаповерхностей описан в [6].

В связи с существующей необходимостью в недорогих электронно управляемых сканирующих антеннах в настоящее время активно ведутся исследования, направленные на создание таких антенн на основе управляемых модулированных метаповерхностей, позволяющих менять направление излучения вытекающей волны за счет изменения средней фазовой скорости поверхностных волн [9–11]. В данной статье описана применяемая авторами методика синтеза подобных антенн на основе элементарных ячеек с двумя степенями свободы, из массива которых и состоит антенна.

Конструкция антенны

В качестве примера для описания методики была синтезирована антенна на частоту 27 ГГц на основе поперечно гофрированной металлической поверхности, поддерживающей распространение поверхностной волны TM типа (рис. 1). Антенна состоит из ячеек, одна из которых показана на вставке рис. 1. Глубина канавок гофрированной структуры описывается параметром ячейки A . Модуляция импеданса метаповерхности осуществляется изменением параметров A индивидуально для каждой ячейки. Направление излучения вытекающей волны зависит от значения параметра ячейки B , который в данном случае обозначает ширину зазора в верхней части ячейки и изменяется для всей антенны целиком. Период структуры d должен быть много меньше длины волны в свободном пространстве А о . Для использованного примера он равен 1.5 мм, то есть 7.4А₀ для частоты 27 ГГц. Излучающая часть антенны состоит из 120 ячеек, длина излучающей части равна 180 мм. Общая ширина антенны - 100 мм. Входной сигнал P ₀ проходит через плоский рупор под структурой, затем переходит на верхний слой, где трансформируется в поверхностную волну над гофрированной поверхностью и излучается за счет взаимодействия с ней. Подобные антенны, однако без возможности управления направлением излучения, описаны, например, в [8].

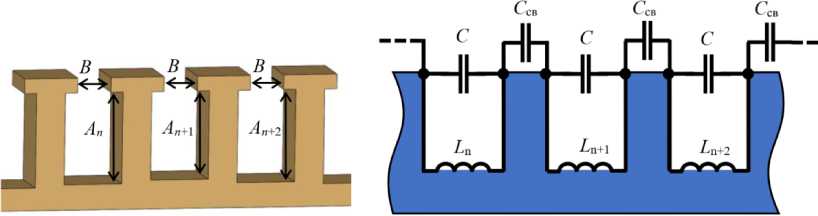
Эквивалентная схема цепочки элементарных ячеек, примененных в данной антенне, показана на рис. 2. Каждая элементарная ячейка представляет собой резонатор, резонансная частота которого зависит от геометрических параметров ячейки. Можно условно выделить эквивалентную емкость ячейки С и ее эквивалентную индуктивность L , а также емкость связи C _св. Параметр A в рассматриваемом примере влияет в основном на величину эквивалентной индуктивности L , а параметр B - в основном на величину эквивалентной емкости C . Вся ан- – 752 –

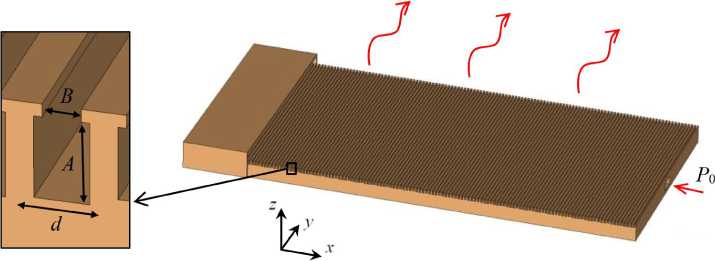
Рис. 1. Модель антенны и элементарная ячейка метаповерхности (на вставке)

Fig. 1. Antenna model and metasurface unit cell (inset)

а                                              б

Рис. 2. Фрагмент метаповерхности ( а ) и его эквивалетная схема ( б )

Fig. 2. Metasurface fragment ( a ) and its equivalent scheme ( b )

тенна, таким образом, представляет собой открытую цепочку сильно связанных резонаторов или замедляющую систему, поддерживающую волну TM типа, а локальный поверхностный импеданс для этой волны определяется параметрами A и B ячеек.

В общем случае параметры A и B могут означать любые две степени свободы ячейки, от которых зависит ее резонансная частота. При этом A – параметр ячейки, используемый для модуляции импеданса метаповерхности, а B – параметр ячейки, с изменением которого происходит изменение угла излучения вытекающей волны. Параметр B одинаков для всех ячеек.

Управляемая емкость C здесь (для общности рассмотрения) реализована за счет геометрии ячейки. На практике же для ее реализации могут быть использованы полупроводниковые варакторы, жидкие кристаллы, сегнетоэлектрики, микроэлектромеханические структуры или другие электрически управляемые элементы. В этих случаях осуществляется электронное сканирование лучом, а параметр B будет обозначать величину подаваемого на управляемые элементы напряжения.

Методика синтеза антенны

Распространение одномерной затухающей электромагнитной волны, в том числе рассматриваемой поверхностной волны TM типа, описывается в общем виде формулой

E ( x,t ) = E 0 e ^-Y x e "  j ^ю t , (1) где у = a + j p , E - комплексная амплитуда колебаний, E _o - начальная амплитуда, у — постоянная распространения, α – постоянная затухания, β – фазовая постоянная, x – координата, ω – угловая частота и t – время. Для поверхностной волны, излучающейся в пространство за счет механизма излучения вытекающих волн, в отсутствие тепловых потерь значение α описывает интенсивность излучения. Значение β связано с фазовой скоростью, а значит, с углом излучения волны [6]. Иначе говоря, контроль значения α позволяет управлять амплитудным распределением поля излучения антенны, а контроль значения β – фазовым распределением. Для контроля значений α и β необходимо определенным образом выбирать параметры A и B ячеек метаповерхности.

Методика синтеза антенны позволяет подобрать для каждой ячейки индивидуальные значения A и для всей антенны общий диапазон значений B , сформировав таким образом необходимые амплитудные и фазовые распределения, и, соответственно, диаграммы направленности. Синтез антенны условно можно разделить на три этапа (рис. 3). Процедура синтеза может быть реализована в программе на языке Matlab и должна использовать для расчета параметров элементарных ячеек и характеристик синтезированной антенны программу электродинамического моделирования, например CST Microwave Studio.

На первом этапе происходит расчет зависимости фазовой скорости волны в ячейке v ph 0 на заданной частоте f 0 от параметров A и B . Расчет проводится при периодических граничных условиях вдоль направления распространения поверхностной волны. Диапазон варьирования параметров выбирают таким образом, чтобы набег фазы на ячейке изменялся в диапазоне от

2 π d

• 1.2 до 0.9π радиан, что соответствует «средним» значениям замедления поверхностной λ 0

волны. В тестовой модели на частоте 27 ГГц параметр A варьировался в диапазоне 1.4–1.64 мм, а параметр B – в диапазоне 0.86–0.95 мм (см. рис. 1).

На втором этапе синтеза с использованием зависимости v ph 0 ( A , B ) рассчитываются различные параметры будущей модели. Из значений фазовой скорости находят эквивалентный поверхностный импеданс Z экв ячеек [12]:

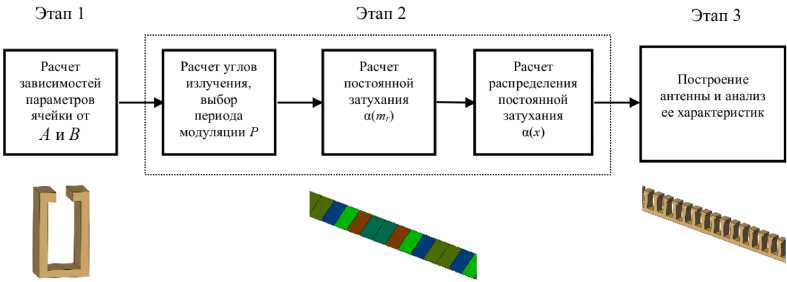
Рис. 3. Этапы синтеза антенны

Fig. 3. Antenna synthesis stages

c2

^Z экв = ^{j 120 n} J - - ¹ • (2) vph 0²

Для гофрированной метаповерхности эквивалентный поверхностный импеданс является индуктивным, то есть имеет мнимую положительную величину. Минимум и максимум импеданса для тестового примера, полученные по формуле (2) из данных расчёта ячейки, равны Z min = j 482 Ом и Z max = j 723 Ом соответственно.

Затем рассчитываются углы направления излучения вытекающей волны для двух крайних значений параметра B в зависимости от периода модуляции эквивалентного импеданса P по всей структуре. На основе этой зависимости выбирается наиболее подходящее значение P . Формула расчета угла направления излучения вытекающей волны m -ой пространственной гармоники θ _m имеет вид [7]

e

m

= arcsin

Pm )

I , V k 0 )

2п                                                                           с где p = p0 + — m - фазовая постоянная для m-ой пространственной гармоники, р0 = к^---- m 0 P                                                        00vph0

фазов ая п остоянная для нулевой пространственной гармоники, k ₀ – волновое число.

В описываемом примере рабочей выступает минус первая пространственная гармоника, поэтому m = –1. Период P выбран равным 6 мм, что соответствует расчетным углам излучения вытекающей волны от 4° до 42°, при этом углы отсчитываются от нормали к поверхности антенны в направлении оси x (см. рис. 1).

Далее с помощью специальной упрощенной модели поверхности с модулированным импедансом рассчитывается зависимость постоянной затухания α от глубины модуляции импеданса m r путем варьирования этой модуляции в структуре с выбранным периодом P . Распределение импеданса в упрощенной модели имеет вид

Z ( x . m ) = Z _o + A Z ■ m_r sin I -^ x I , экв         r          0               r

P

(Z + Z

Z max    m i n

0 = --------- , ^Л Z =

—

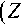
Z - )

^{m i n} . Величина α рассчитывается из S-параметров упро-

щенной модели.

Далее находится необходимая для реализации заданного амплитудного распределения зависимость постоянной затухания α от координаты x . Когда метаповерхность имеет одинаковую глубину модуляции импеданса по всей длине, α не меняется с изменением координаты x , а поле излучения антенны имеет экспоненциально спадающее амплитудное распределение. Такое амплитудное распределение приводит к низкой эффективности, поэтому конструкция антенны должна реализовывать изменение α в зависимости от x для получения заданного амплитудного распределения [7]:

a ( x ) =---- ™----^^ ( x )-------------.

• ² 7mP°kk) J o^{| £} ®^|- d ^6—№ ®^|- d ⁵ P ^(o) P ⁽ L )

где E(x) – заданное амплитудное распределение поля, P(0) – мощность на входе антенны, P(L) – не излученная антенной мощность (обычно задается как 10 % от P(0)), L – длина излучающей части антенны, ξ – переменная интегрирования. Для антенны, использованной для примера, задавалось линейно спадающее амплитудное распределение. При этом считается что зависимость α(x), а значит, и амплитудное распределение, не зависят от направления излучения вы,,         , текающей волны.

На третьем этапе на основе полученных данных строится зависимость параметра A каждой ячейки от ее координаты. При этом, по сути, выполняют шаги второго этапа синтеза в обратном порядке (рис. 4).

В итоге описанной процедуры синтеза получаются все необходимые данные для создания трехмерной модели антенны, которая строится в программе электродинамического моделирования, где затем проводится расчет ее характеристик. Результат расчета диаграмм направленности модели антенны, использованной в качестве примера (см. рис. 1), в зависимости от значения параметра B показан на рис. 5. Диаграммы направленности приведены для плоскости XZ , в которой происходит сканирование. Как видно, направление излучения вытекающей волны равно 4° при B =0.865 мм и 42° при B =0.955 мм, что достаточно близко к тем значениям, кото-

Рис. 4. Получение координатной зависимости параметра A из рассчитанных данных

Fig. 4. Obtaining the coordinate dependence of parameter A from the calculated data

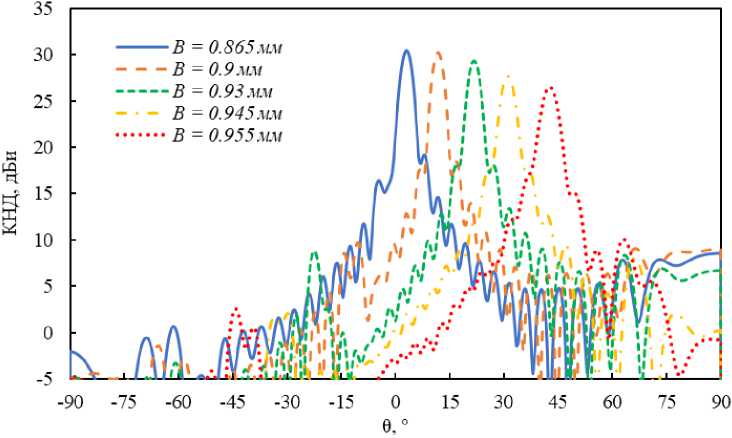
Рис. 5. Рассчитанные диаграммы направленности синтезированной антенны

Fig. 5. Calculated radiation patterns of the synthesized antenna рые были рассчитаны на втором этапе синтеза (от 4.5° до 44°). Коэффициент направленного действия антенны составил от 26.4 до 30.1 дБи, что соответствует апертурной эффективности от 24 до 56 %.

Заключение

Описанная в работе методика позволяет синтезировать одномерно сканирующие антенны на основе метаповерхностей, состоящие из элементарных ячеек с одним управляемым параметром. В качестве такого параметра удобно использовать емкость ячейки, которая может динамически управляться различными элементами, например полупроводниковыми или сегнетоэлектрическими варакторами. При этом необходимую для получения вытекающей волны синусоидальную модуляцию импеданса поверхности можно получать, управляя индуктивностью ячеек с помощью статичного параметра, задаваемого для каждой ячейки индивидуально. Такой подход позволяет относительно просто, по сравнению с фазированными антенными решетками, получить электронное сканирование лучом антенны. Методика использует ряд допущений, например о независимости постоянной затухания α от направления излучения вытекающей волны, которые снижают точность реализации требуемых амплитудных и фазовых распределений. Коррекция приведенной методики для более точной реализации необходимых амплитудных и фазовых распределений и получения большей апертурной эффективности в антеннах описываемого типа станет целью последующей работы.