Методика синтеза регуляторов для объектов второго порядка

Введение. Синтез регуляторов систем автоматического управления (САУ) – одна из основных предметных задач теории автоматического управления. Наибольшее распространение в САУ технологическими процессами получили пропорционально-интегрально-дифференцирующие (ПИД) регуляторы.

Из многочисленных источников научной и технической литературы можно выделить следующие методы синтеза ПИД-регуляторов [1–10]: эмпирическая настройка; методы Зиглера–Никольса [1] и производные методы [2]; алгебраические методы; методы модального синтеза; методы синтеза в частотной области; методы оптимального синтеза; метод оптимальной ПФ замкнутой системы (технический и симметричный оптимумы). Основные тенденции развития методов синтеза ПИ- и ПИД-регуляторов представлены в книге Aidan O’Dwyer 2006 г. [7] (443 метода синтеза ПИД-регуляторов) и в издании Aidan O’Dwyer 2009 г. [8] (1731 метод синтеза ПИД-регуляторов).

Одним из методов синтеза ПИД-регуляторов, активно развиваемый учеными, является модальный метод [3; 9]. В научных работах, посвященных синтезу регуляторов, отсутствуют соотношения, связывающие значения переходной характеристики и коэффициентов объекта управления с учетом расположения действительных полюсов.

Наиболее распространенными для мобильных, строительных, дорожных, дорожно-строительных машин как объектов управления являются математические модели второго и более высокого порядка [9–13].

Исходное математическое описание системы и постановка задачи. Рассматривается линейная система автоматического управления с передаточной функцией (ПФ) объекта второго порядка.

Передаточная функция объекта управления второго порядка W о ( s ) и ПИД-регулятора W_y ( s ) имеют вид

W o ( » ) =

b 0 ⁵ + b

2 ;

a 0 5 + a_i s + a 2

W y ⁽ s ) = K p + K i- + K d S = s

K d S ² + K p s + K

s

где s – символ преобразования Лапласа; K_p , K_i и K_d – коэффициенты соответственно пропорциональности, интегрирования и дифференцирования.

При последовательном соединении ПФ объекта и ПИД-регулятора образуется разомкнутая система с ПФ следующего вида:

W ( s ) = W o ( s ) W y ( s ) =

K d b о s ³ + ( K d b i + K p b ₀) s ² + ( Kb о + K p b i ) s + K b i

3          2                                           .

a ₀ s + a_i s + a ₂ s

ПФ замкнутой системы управления с единичной обратной связью

K ( s ) =

W ( s ) 1 + W ( s )

Kb s ³ + ( Kb + Kb > s ² + ( Kb + Kpb,) s + Kb

⁽ a ⁺ K d bi)^{s 3 + (} a i ⁺ K d b i ⁺ K A) ^{s 2 + (} a 2 ⁺ Kb ⁺ K p b i )^{s +} Kb

Исходными данными для синтеза ПИД-регулятора САУ являются ПФ объекта управления Wо (s) второго порядка и заданные показатели качества: перерегулирование и время регулирования.

Решается задача определения значений коэффициентов ПИД-регулятора Kd,Kp,K , обеспечивающих заданные показатели качества по заданным ПФ объекта управления второго порядка Wо (s) и зна- чениям действительных полюсов si = -ni, s2 = -n2, s3 = -n3 ПФ замкнутой системы управления.

Вывод основных соотношений. ПФ замкнутой системы с ПИД-регулятором при задании действительных полюсов представим в виде

K ( s ) =

= K d b о s ³ + ( K d b i + K p b о ) s ² + ( Kb о + K p b i )s + Kb (1) ^{( a} о ^{+ K} d ^b о^{)( s +} П 1^{)( s +} П 2Х ^{s +} П э )        .

Введем обозначения с целью упрощения выражения (1):

K d b о ; b = K d b i ⁺ K p b о ; ^a о ^{+ K} d ^b о’ ^{Oi a} о ^{+ K} d ^b0 ’

Kb о + K p b i _; b = Kb i ^a о ^{+ K} d ^b о ’ ^{03 a} о ^{+ K} d ^b 0

С учетом обозначений (2) получим в области изображений для переходной характеристики h(s) замкнутой системы с ПИД-регулятором при задании значений действительных полюсов h (s) = Ьоо s + bо1 s + bо2 s + bоэ

^{( s +} n i^{)( s +} П 2^{)( s +} П э ) ^s '

Характеристическое уравнение замкнутой системы имеет третий порядок. При известных заданных значениях действительных полюсов si =-ni;s 2 =-П2;s з =-Пэ.

Это уравнение имеет следующий вид:

D d ^{( s} ) = ^{( s} - ^s i^{)( s} - ^s 2^{)( s} - ^s 3 ).              ⁽³⁾

Выполнив операцию Collect программы MathCAD, обеспечивающей замену выражения (3) выражением, скомплектованным по базису переменной, получим следующее выражение:

D_d ( s ) collect, s ^ s ³ + (n_i + n₂ + П 3 ) s ² +

^{+ [} П з⁽ П 1 ⁺ n 2⁾⁺ n i n 2^{] s +} n i n 2 П э .

К такому виду приводится характеристическое уравнение корректируемой системы:

⁽ 0 )^{+ K} d ^b 0^{) s 3 + ( a} i ⁺ K d b i^{+ K} p ^b o^{) s 2 + (} a 2^{+ K} _l ^b 0 ⁺ K p b i ) ^{s + K}b i 0 )^{+ K} d ^b 0

3 f ai + Kdbi + Kpbo К = s +1I s +

I ^a о ^{+ K} d ^b о )

' a 2 ^{+ K} b о ⁺ K p b i )      Kb

I s +.

, ^a о ^{+ K} d ^b о J ^a о ^{+ K} d ^b 0

Приравнивая коэффициенты при одинаковых степенях s , получим следующие равенства:

a + K d b i + K p b 0 a 0 + K d b 0

a 2 + K i b 0 + K p b i a 0 + K d b 0

= n i + n + П з ;

= П з (П 1 + П 2 ) + П 1 П 2 ;

K i b 1

a 0 + K d b 0

= П 1 П 2 П з -

Определим установившееся значение h_stab переходной характеристики h ( t ) при задании действительных полюсов в соответствии с теоремой предельного перехода:

lim( 5 ■ h ( 5 )) i---------- i -¹--------;

^s ’"              П 1 П 2 П з⁽ a 0 + K d b 0 )

Определение составляющих переходной характеристики замкнутой САУ с ОУ второго порядка. Определим составляющие переходной характеристики h ( t ) замкнутой системы с ПИД-регулятором при задании действительных полюсов в среде программы MathCAD:

lim [ ( s + n) h ( s ) ] simplify i s i- щ

⁽ b 1 ^- b 0 П 1Х K d П 2 ^- K p П 1 ⁺ K i )

i-------------------------;

П 1⁽ П 1 ^- П2ХП 1 ^- П з⁾⁽ a 0 ⁺ K d b 0 )

lim [(s + п2 )h(s)] simplify i s ^-П2

( b - b 0 П 2 )( K d П 2 - K p П 2 + K i )

i--------------------------;

П 2⁽ П 1 ^- П2ХП 2 ^- П з⁾⁽ a 0 ⁺ K d ^b 0 )

тогда установившееся значение h_stab

. = stab

^K i ^b 1          .

П 1 П 2 П з⁽ a 0 + K d b 0 )-

lim [ ( s + П_з) h ( s ) ] simplify ^

( b 1 - b 0 П з )( K d П з2 - K p П з ⁺ K ) i-------------

.

В соответствии с равенством (5)

Kb

-----= П 1 П 2 П з , a 0 + K d b 0

подставляя (7) в (6), получим h = Kb       = П1П2 Пз = 1

^5tab П 1 П 2Ы a 0 + K d b 0 ) П 1 П 2 П з

.

П з⁽ П 1 ^- П з⁾⁽ П 2 ^- П з⁾⁽ a 0 ⁺ K d b 0 )

Обозначим установившееся значение h_stab в соответствии с (6)

/7 . = stab

_ib ₁

П 1 П 2 П з⁽ a 0 ⁺ K A)’

Полученный результат (8) подтверждает, что рассматриваемая замкнутая система управления является астатической относительно входного воздействия.

Определим начальное значение h_init переходной

тогда составляющая h η₁ ( t ), обусловленная полюсом s 1 = –η 1 ,

, „ ^{( b} 1 ^{- b} 0 П 1⁾⁽ K d П 1^{2 -} K p П 1 ⁺ K i ) . h _П ( t ) =------------------------------------ e

¹       П 1⁽ П 1 ^- П 2⁾⁽ П 1 ^- П з⁾⁽ a 0 ⁺ K d b 0 )

'^{-П 1} t ; (9)

характеристики h ( t ) в соответствии с теоремой предельного перехода для случая задания действительных полюсов:

lim( s ■ h 1 ( s )) i K d b ⁰   ,

⁵ ^”            a 0 + K d b 0

т. е.

K d b 0

init               Tr 1   - a 0 + Kdb0

составляющая h η2 ( t ), обусловленная полюсом s 2 = –η 2 ,

, „ ^{( b} 1 ^- b 0 П 2⁾⁽ K d П 2^{2 -} K p П 2 ⁺ K i ) - h _П, ( t ) =------------------------------------- e

²       П 2⁽ П 1 ^- П 2⁾⁽ П 2 ^- П з⁾⁽ a 0 ⁺ K d b 0 )

■^{-П 2} t ; (10)

составляющая h η3 ( t ), обусловленная полюсом s 3 = –η 3 ,

, „ (b1 -Ь0Пз)(KdПз2 -KpПз + Ki) _ hП (t) =---------------------------------e з      Пз(П1 -Пз)(П2 -Пз)(a0 + Kdb0)

,^-П з t

Доказано, что для рассматриваемой задачи синтеза ПИД-регулятора системы управления с ОУ второго порядка справедливо условие h init <  h ( t ) <  1 при установившемся значении h_stab = 1. Это выражение не зависит от типа заданных полюсов.

Таким образом, значение переходной характеристики замкнутой системы с ПИД-регулятором изменяется во времени от h_init до h_stab = 1. При этом если значение b 0 = 0 , то начальное значение переходной характеристики h_init = 0 .

Очевидно, что при некотором значении b ₀ h_init войдет в 5%-ную зону установившегося значения. Это свидетельствует о возможности значительного уменьшения времени переходного процесса при b ₀ не равном 0.

Таким образом, для случая действительных полюсов выражение переходной характеристики h ( t ) примет следующий вид:

^{h (} t ) = h init ⁺ h n ⁽ t ) ⁺ h n₂⁽ t ) ⁺ h п_з⁽ t ) -

Методика синтеза ПИД-регулятора для случая действительных полюсов. Значения всех трёх полюсов являются действительными:

^s 1 =^- П 1 ; ^s 2 = ^- П 2 ; ^s з =^- П з -

Представим равенства (5) в виде системы уравнений, в которой неизвестными являются значения коэффициентов ПИД-регулятора:

K d ^{[ b} 1 ^- b 0 СП 1 + П 2 ⁺ П з^{)] +} K p b 0 = a 0⁽ П 1 + П 2 ⁺ П з ) ^{- a} 1 ;

^- K d b 0 ( П з⁽ П 1 ⁺ П 2 ) ⁺ П 1 П 2 ) ^{+ K} p b 1 ⁺ K i b 0 =

= a 0⁽ П з⁽ П 1 ⁺ П 2 ) ⁺ П 1 П 2 ) ^- a 2 ;

^- K d b 0 П 1 П 2 П з + Kb = a 0 П 1 П 2 П з -          ⁽¹³⁾

Введем обозначения с целью представления системы уравнений (13) в матричной форме:

^Xn = b ^- b A + П 2 + П з ); ^ 12 = b 0 ;

^X 13 = 0; C i = a о (П 1 + П 2 ⁺ П з ) ^- «V;

^ 21 =^- b 0 ( ПзОи + П 2 ) ⁺ П 1 П 2 ) ; ^ 22 = b 1 ;

^X 23 = b 0 ; ^C 2 = a 0⁽ П з⁽ П 1 ⁺ П 2 ) ⁺ П 1 П 2 ) ^- a 2 ;

^X 31 = b 0ⁿ1ⁿ2^Пз ; ^X 32 = ^{0; X} 33 = ^b 1 ;

^C 3 = ^a 0 П 1 П 2 П 3 .

С учетом о	бозначений	(14) сформируем матрицы:
'^ 11 Л d = ^ 21	^ 12    ^ 13 ^ X 22    X 23	fCl      ( K d 1 ; c d = = 2. ; к 1 = к , , (15)
4^ 31	X 32    Х зз у	1 C 3 J       1 Ki у

где Л _d и C d - матрица и вектор-столбец известных параметров объекта управления и заданных значений действительных полюсов соответственно; К ₁ – вектор-столбец искомых значений коэффициентов ПИД-регулятора.

Матричное уравнение для определения искомых значений коэффициентов регулятора имеет вид

(Л d ■ K1) = Cd, а его решение представляется в виде

K 1 =Л d ^{- 1} C d .

Система уравнений (5) значительно упрощается при b ₀ = 0:

a + K_db

-—— = П 1 + П 2 + П з ;

a 0

a ₂ + K_pb 1

-----------= П 3 СП 1 ⁺ П 2 ) ⁺ П 1 П 2 ;

a 0

K

-----= П 1 П 2 П 3 .

a 0

В этом случае формулы для определения значений коэффициентов ПИД-регулятора имеют следующий вид:

C 1 a 0⁽ П 1 + П 2 ⁺ П з ) ^- a 1 .

Ka = -- = ------------------;

^d b 1 b 1

- = c ₂ = a 0 [ П з (П 1 + П 2 ) + П 1 П 2 ] - a 2 . ^{p b} 1 ^b 1 ;

K = C 3 = a 0 П 1 П 2 П з ⁱ b ₁ b ₁

Получены выражения для расчета коэффициентов ПИД-регулятора, включающие коэффициенты ПФ объекта второго порядка при заданных значениях действительных полюсов. Выполнена проверка рассмотренной методики на конкретном примере.

Пример 1. Задан объект управления второго порядка с ПФ

W o ( » ) =

b ₀ 5 + b 1

a ₀ 5 + a 1 5 + a ₂

0,01 5 + 0,7 0,04 5 ² + 0,12 5 + 1"

Требуется синтезировать ПИД-регулятор, который обеспечит переходную характеристику без перерегулирования, а время регулирования t p = 3 c.

Для реализации метода синтеза применены зависимости (11), (12). Расчеты выполнены в среде программы MathCAD.

Исходные данные для действительных значений полюсов: значение η1 определено с учетом желаемого времени регулирования, равного 3 с, и расчета по известной приближенной формуле [14–16]:

t _р

3 Re( s ),

П 1 = Re ⁽ 5 ),

где Re( s )– действительная часть полюса, наиболее приближенного к мнимой оси корневой плоскости; значения η₂ и η₃ определяются из требуемого значения перерегулирования и влияния этих полюсов на полюс η₁ :

П 1 = 1; n₂ = 4; n₃ = 5; b = 0,7; b ₀ = 0,01; a ₀ = 0,04; a 1 = 0,12; a ₂ = 1,0.

Для заданных действительных полюсов определены коэффициенты ПИД-регулятора

	f K d 1		' 0,46 л
К 1 =	K p	=	0,401	;
	. K i у		. 1,274 >
K d = 0,46;	K p =	0,401; Ki		= 1,274

Установившееся значение h_5tob = 1.

Выполнено моделирование переходного процесса для периода времени t = 0–5 с, шаг 0,001 с.

Cоставляющие hη1 (t), hη2 (t), hη3 (t), обусловлен- ные действительными полюсами 51 = - n1, 52 = - п2, 53 = — П3, определяются по зависимостям (9)-(11).

Переходная характеристика h ( t ) при заданных действительных полюсах получена по выражению (12).

При t = ⁰ получим h ( t ) = h 5tab + h n 1 ( t ) + h n ₂( t ) + + h n ₃( t ) = 0,973.

Начальное значение h_init переходной характеристики h ( t )

^h init

K d b ⁰ = 0,973 ^a 0 ⁺ K d b 0

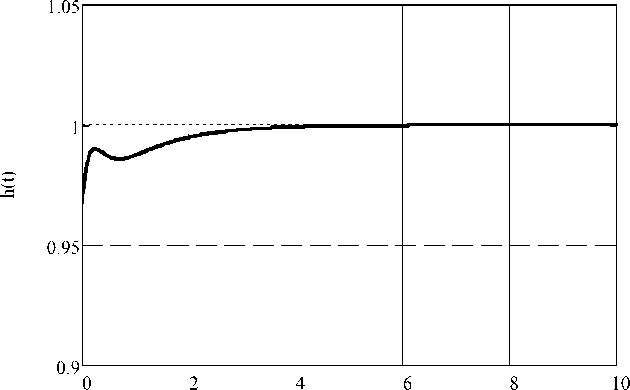
На рис. 1 представлен график переходной характеристики h ( t ) замкнутой САУ с синтезированными параметрами ПИД-регулятора.

Пример 2 . Исследование переходного процесса при изменении значения полюса η₁ .

Для исследования влияния на переходный процесс системы заданного значения действительного полюса

η₁ в диапазоне 1–4 проведено моделирование для периода времени t = 0,0.001 - 5.

На рис. 2 представлен график переходной характеристики h ( t ) замкнутой САУ с синтезированными параметрами ПИД-регулятора при заданных значениях полюса П 1 ( etal) = 1,2, 3,4 .

Пример 3 . Исследование переходного процесса при изменении значения коэффициента b ₀ ПФ объекта управления. Для исследования влияния на переходный процесс системы значения коэффициента b ₀ ПФ объекта управления в диапазоне 0,10–0,80 проведено моделирование для периода времени t = 0,0.001 - 5.

Результаты моделирования переходного процесса h(t) замкнутой САУ с синтезированными параметрами ПИД-регулятора приведены на рис. 3 при задан- ных значениях коэффициента b0 ПФ ОУ. Получены следующие оценки переходной характеристики с учетом 5%-ной зоны:

время регулирования:

t _р = 0 c при b ₀ = 0,10;

t _р = 0,08 c при b ₀ = 0,20;

t _р = 1,69 c при b ₀ = 0,30;

t _р = 1,75 c при b ₀ = 0,40;

t _р = 1,59 c при b ₀ = 0,50;

t _р = 0,69 c при b ₀ = 0,60;

t _р = 0 c при b ₀ = 0,70;

t _р = 1,0 c при b ₀ = 0,80.

t, s

Рис. 1. График переходной характеристики синтезированной системы с заданными действительными полюсами

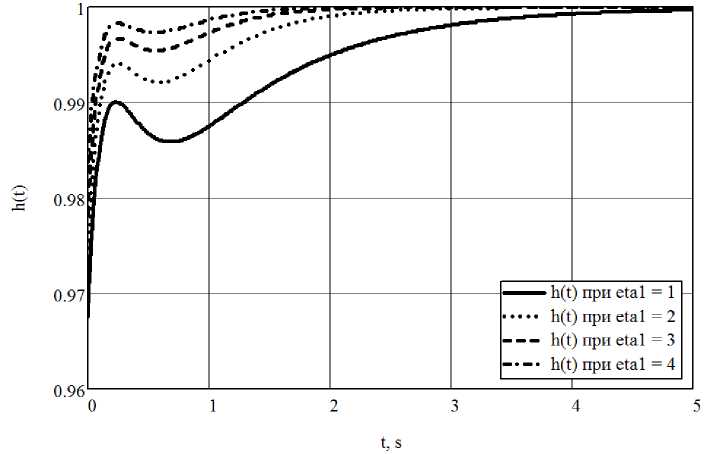
Рис. 2. Графики переходной характеристики синтезированной системы с заданными действительными полюсами при значениях полюса П1 (eta1) = 1, 2, 3, 4

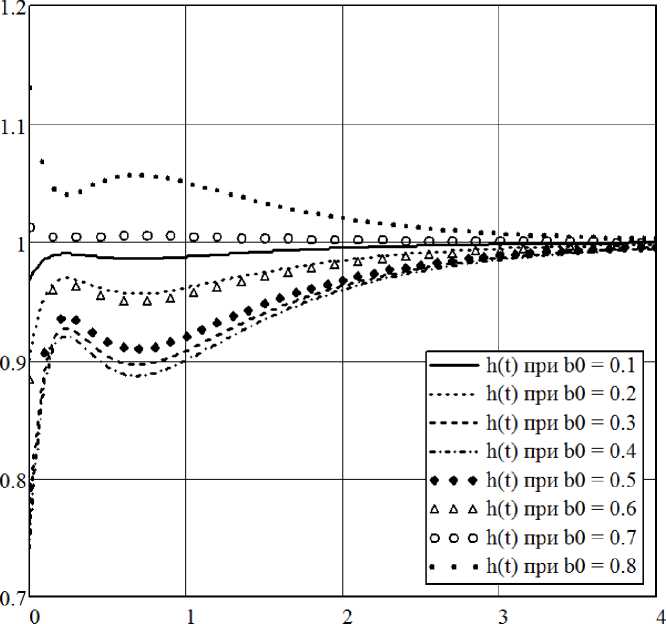
Рис. 3. Графики переходной характеристики синтезированной системы с заданными полюсами при значениях коэффициента b ₀ ПФ объекта управления в диапазоне 0,10–0,80

Увеличение значения коэффициента b ₀ ПФ ОУ больше 0,7 приводит к появлению перерегулирования. При значении коэффициента b ₀ , равном 0,8, переходная характеристика начинается с h (0) = 1,13 , появляется перерегулирование. Полученные результаты показывают возможность прогнозирования коэффициентов ПФ ОУ с учетом значений коэффициентов ПИД-регулятора.

В соответствии с разработанной методикой синтеза ПИД-регулятора переходный процесс носит апериодический характер. При известном значении b ₀ , заданных параметрах объекта второго порядка и действительных полюсов в рассмотренном в примере время переходного процесса, исходя из условия 5%-ной зоны установившегося значения, равно 0 с.

Заключение. Предложен метод модального синтеза параметров ПИД-регулятора по заданным значениям параметров объекта второго порядка и действительных полюсов замкнутой системы управления. Методика синтеза реализована в программной среде MathCAD.

Имитационное моделирование показало, что при некотором значении b ₀, не равном 0, начальное значение переходной характеристики h_init войдет в 5%-ную зону установившегося значения. Это свидетельствует о возможности значительного уменьшения времени переходного процесса.