Методика снижения погрешности автоколебательного акселерометра

Повышение точности и достоверности определения значений физических величин представляет собой одну из важных задач совершенствования измерительных устройств. Решение этой задачи во многом определяет степень надежности и безопасности функционирования сложных технических объектов.

В различных измерительных устройствах используется компенсационный метод из мерения соответствующей физической величины [4]. Дос тижение низкой погрешности

Методика снижения погрешности автоколебательного акселерометра

Ватутин Михаил Алексеевич кандидат технических наук, доцент, доцент кафедры автономных систем управления. Военнокосмическая академия имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: командные приборы; техническая электроника; схемотехника электронных устройств автономных систем управления. Автор 90 опубликованных научных работ.

измерения физической величины в классическом датчике базируется на использовании в своем составе высокоточных механических и электронных элементов. В то же время существуют методические погрешности, которые вносят погрешность в измерение сигнала вне зависимости от точностных параметров применяемых элементов [13]. Одной из таких методических погрешностей, оказывающих значительное влияние на погрешность преобразования, является погрешность преобразования аналогового измеряемого сигнала в цифровой код. Для снижения методической погрешности важную роль играет режим работы преобразовательного устройства

Цель данной статьи – разработка методики снижения методической погрешности автоколебательного акселерометра.

Постановка задачи

При производстве инерциальных датчиков, в частности акселерометров, измерительное устройство, как правило, выполняется как линейное [5], у которого выходным сигналом является аналоговый сигнал.

Типовая структурная схема маятникового акселерометра, работающего в линейном режиме, показана на Рисунке 1.

Маятник связан с неподвижным основанием (НО) через упругий торсион (Т). Чувствительным элементом маятникового акселерометра является инерционная масса (маятник М), отклоняющаяся под воздействием ускорения на некоторый угол ±р Л . Измеряемое акселерометром ускорение определяется выражением

_ ^кд.м .

aBX =    , iд.м , ml где m – масса маятника; l – длина плеча маятника; kД.М – коэффициент передачи датчика момента; iД.М – ток датчика момента.

Для согласования инерциального датчика с бортовой цифровой вычислительной машиной (БЦВМ) применяются аналого-цифровые преобразователи (далее – АЦП) или различные специальные режимы работы чувствительного элемента датчика [7]. Применение АЦП для регистрации отсчетов с частотой fS приводит к появлению специфической погрешности, свойственной любому АЦП, – погрешности (шуму) квантования [2; 10; 15], показанному на Рисунке 2, а.

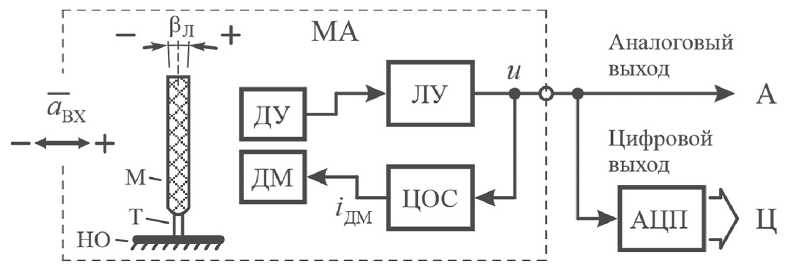
Рисунок 1. Структурная схема маятникового акселерометра, работающего в линейном режиме: ДУ – датчик угла; ДМ – датчик момента; ЛУ – линейный усилитель; ЦОС – цепь обратной связи

Для снижения шума квантования применяются различные цифровые фильтры, которые путем применения вероятностных методов оценки сигнала позволяют распределить шум квантования в более широкой полосе частот Kf _S/2 и тем самым снизить его в заданной полосе частот f _S/2 (см. Рисунок 2, б ).

Шум квантования

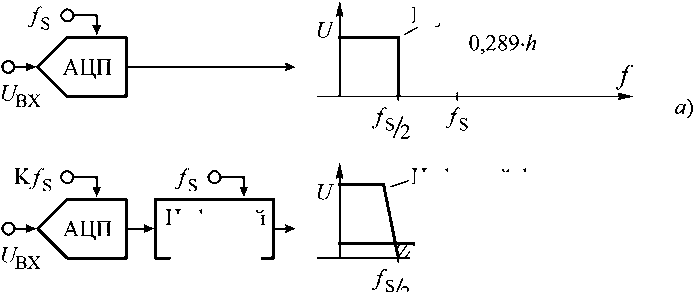
б)

K/s

Цифровой фильтр

Цифровой фильтр

Удаленный шум

2    K/s/2

Рисунок 2. Шум квантования, возникающий при аналого-цифровом преобразовании: а – шум квантования; б – распределение шума квантования в полосе частот

Использование цифрового фильтра требует некоторых вычислительных мощностей, которые берутся либо в бортовом вычислителе и потребляют его ресурсы, либо цифровой фильтр выполняется как самостоятельное цифровое устройство, построенное на отдельном микроконтроллере. Необходимо разработать методику построения акселерометра, позволяющую снизить шум квантования без применения цифрового фильтра.

Решение задачи

Автоколебательный режим работы маятникового акселерометра [1; 4; 14] по сравнению с классическим (см. Рисунок 1) имеет следующие преимущества:

• значительно снижается порог чувствительности акселерометра, так как уменьшается влияние различного рода нелинейностей в подвесе чувствительного элемента;

Методика снижения погрешности автоколебательного акселерометра

• значительно упрощается построение преобразователя (измеряемое ускорение ^ цифровой код), так как информация о значении измеряемого ускорения переносится во временную область.

Информация о величине измеряемого ускорения за период автоколебания T _{0 i} содержится [7] во временных интервалах t _{1 i} , t _{2 i} , T _{0 i} :

a BX i

- knp

■ U нз ( t 1 i t 2 i )/ T O i ,

где k _np - коэффициент преобразования, U _нз - напряжение на выходе НЗ.

Погрешность квантования преобразования дискретного сигнала

В работе [8] показано, что в режиме перекомпенсации происходит изменение длительности временных интервалов t _{1 i} и t _{2 i} до значений t ₁ ^* _i и t ₂ ^* _i , что приводит к изменению величины компенсирующего момента:

И* + *        - *

^М И i ^- M OC i ⁺ M OC i .                                (3)

В результате при перекомпенсации на i -м периоде колебаний выражение (3) не соблюдается, и величина компенсирующего момента M ^И не будет равна моменту инерционных сил _ _ и* _ _и

M и i * M И i ;                                          (4)

возникает погрешность компенсирующего момента:

И*     И  игИ*

^ ( ^М И i ) ^- M И i ^М И i

**

Если значения t1i ( t2i ) меньше значения t1i ( t2i ), то маятник отклоняется на меньший относительно исходного автоколебательного режима угол РАК. Таким образом, угол вАкi отклонения маятника в режиме перекомпенсации не имеет постоянной величины и носит случайный характер.

Соответственно, преобразованный цифровой сигнал (временной интервал t ₁ ^* _i и t ₂ ^* _i ) по цепи обратной связи оказывает большее по величине воздействие на движение маятника. Дополнительная величина момента А ( M ^И i ) в данный i -й интервал времени выступает как погрешность измерения, но учитывается при измерении следующего ( i +1)-го и последующих временных интервалах. Суммирование ошибки по результатам предыдущих периодов автоколебаний позволяет исключить погрешность квантования по времени.

Особенности работы сигма-дельта АЦП

Из [2; 3; 10; 12; 13; 15] известно, что сигма-дельта АЦП среди всех существующих типов АЦП имеют наибольшее разрешение – до 24 действующих разрядов. Повышение количества разрядов происходит за счет снижения шума квантования. Один из принципов, заложенных в этот АЦП, позволяющий уменьшить погрешность, вносимую шумом квантования, и, следовательно, увеличить разрешающую способность, – это усреднение результатов измерения за счет уравновешивания заряда на большом интервале времени.

На Рисунке 3 показана функциональная схема сигма-дельта АЦП первого порядка.

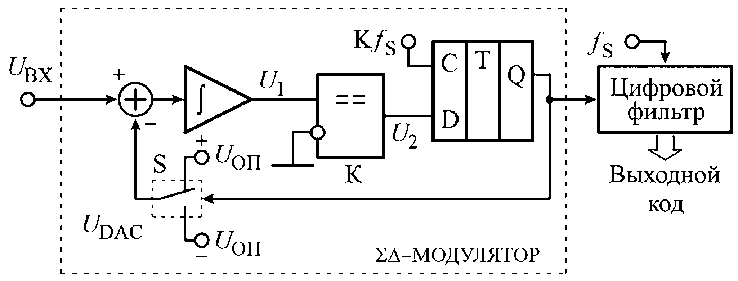
Рисунок 3. Функциональная схема Σ∆ -АЦП первого порядка

На Рисунке 4 показана шум (ошибка) квантования в Σ∆ -АЦП [2; 10; 15].

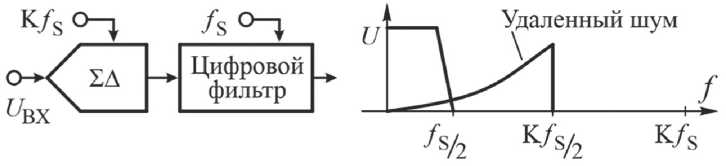
Рисунок 4. Снижение шума квантования Σ∆ -АЦП первого порядка

Анализ работы маятникового акселерометра, работающего в автоколебательном режиме с перекомпенсацией, показывает, что этот режим соответствует принципу работы сигма-дельта АЦП ( Σ∆ -АЦП) [3; 12].

Маятниковый акселерометр в режиме работы Σ∆ -АЦП

Структурная схема маятникового акселерометра, работающего в режиме Σ∆ -АЦП преобразователя, показана на Рисунке 5.

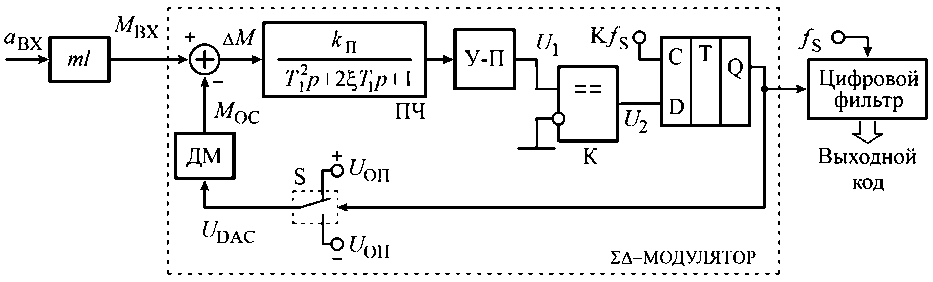
Рисунок 5. Структурная схема маятникового акселерометра, работающего в режиме Σ∆ -АЦП преобразователя

Величину входного ускорения а _ВХ во входной момент М _ВХ преобразует маятник с массой m и плечом l . Момент обратной связи М _ОС формируется в датчике момента (ДМ) при подключении его к источникам опорного напряжения U _ОП при помощи ключа S . Для преобразования перемещения маятника в электрический сигнал введен усилитель-преобразователь (У-П).

Для автоколебательного акселерометра инерционные свойства маятника одновременно являются и интегратором (инерционность маятника значительно выше инерционно-

Методика снижения погрешности автоколебательного акселерометра сти управляющих сигналов и тактовых частот), и сумматором (маятник своим пространственным движением суммирует входной момент инерционных сил и момент, возникающий по цепи компенсации входного воздействия (цепи обратной связи)).

Одна из сложностей реализации в полной мере в акселерометре режима работы Σ∆ -АЦП – широкий диапазон изменения величины компенсирующего воздействия. Для достижения в полной мере в акселерометре возможностей Σ∆ -АЦП необходимо импульсным способом изменять ток i _ДМ в диапазоне значений ± 2²⁴.

Автоколебательный акселерометр в режиме работы Σ∆ -АЦП

Структурная схема маятникового акселерометра, работающего в автоколебательном режиме с устройством синхронизации, создающим перекомпенсацию входного воздействия, показана на Рисунке 6.

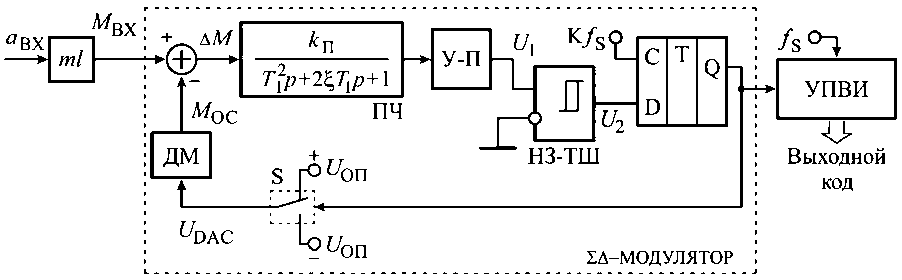
Рисунок 6. Структурная схема автоколебательного акселерометра в режиме перекомпенсации

Отличие данной схемы от схемы Σ∆ -АЦП состоит в том, что вместо компаратора К используется нелинейное звено (триггер Шмитта) НЗ-ТШ. Постоянная времени Т ₁ подвижной части маятникового акселерометра значительно больше временных интервалов ∆ ( t ₁ ⁰ _i ^,1 ) или ∆ ( t ₁ ¹ _i ^,0 ). Поэтому передаточную функцию подвижной части акселерометра по отношению к этим временным интервалам можно представить как двойной интеграл w ( p ) * k n 1 2² ,                                   (6)

где ^к П = k n/ T 2 , инерционность которой интегрирует сумму моментов, приложенных к ней, и преобразует сумму приложенных моментов в параметры движения маятника.

Шум квантования [3; 12] для усилительной системы второго порядка ниже, чем для системы первого порядка. На практике [2; 10; 15] для повышения точности преобразования порядок системы повышают, и действующие Σ∆ -АЦП имеют 3-й, 5-й и 7-й порядок. Дальнейшее увеличение порядка системы в Σ∆ -АЦП не применяется в связи со сложностью обеспечения устойчивости работы преобразователя. Кроме того, повышение порядка системы приводит к снижению максимальной полосы преобразования Σ∆ -АЦП.

Моделирование работы автоколебательного акселерометра

Для подтверждения теоретических предположений, рассмотренных выше, было произведено моделирование автоколебательного акселерометра, работающего в режиме пе-рекомпенсации, в моделирующем пакете MATLAB. Структура модели акселерометра показана на Рисунке 7.

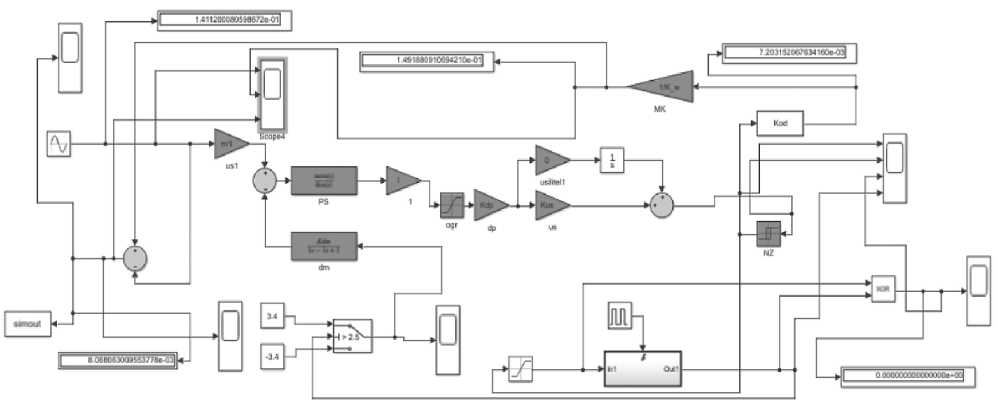
Рисунок 7. Модель автоколебательного акселерометра в пакете MatLab

Результаты моделирования ошибки квантования u _{∆ (Т)} показаны в таблице.

Таблица

Результаты моделирования для f _ГТИ = 100 кГц

x	–3,0	–2,5	–2,0	–1,5	–1,0	–0,5	0	0,5	1,0
f ВХ , Гц	0,001	0,00316	0,01	0,0316	0,1	0,316	1,0	3,16	10,0
u ∆ (Т)	0,002	0,003	0,004	0,005	0,01	0,015	0,04	0,1	0,4

Для создания модели были использованы численные данные параметров акселерометра А-15, приведенные в [11]. Моделирование проводилось для тактовой частоты f _ГТИ = 100 кГц. Невысокое значение тактовой частоты не изменило сути происходящих процессов, но позволило значительно сократить время на моделирование модели. Частота изменения входного (измеряемого) ускорения f _ВХ изменялась дискретно от 0,001 до 10 герц в логарифмическом масштабе: f _ВХ = 10^x.

На Рисунке 8 результаты моделирования представлены в двойном логарифмическом масштабе.

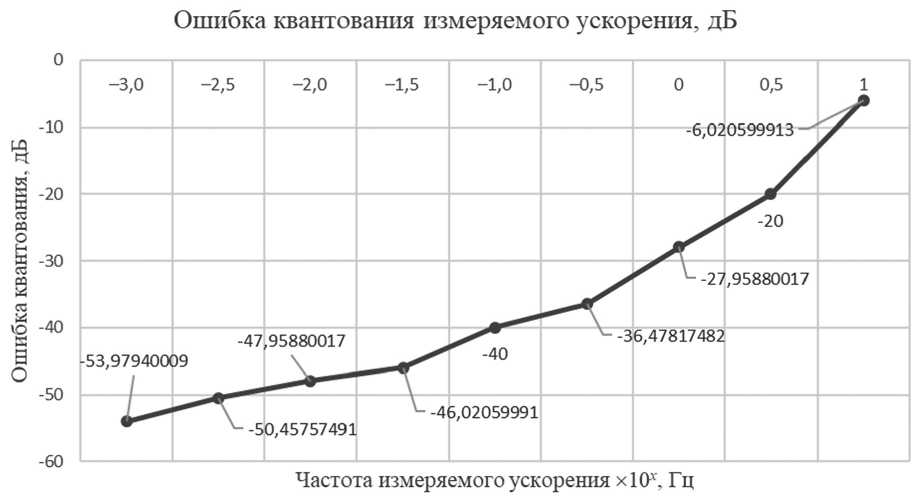
Рисунок 8. Зависимость ошибки квантования от частоты входного сигнала

Методика снижения погрешности автоколебательного акселерометра

Крутизна характеристики ошибки квантования для Σ∆-АЦП составляет 40 дБ/дек [2; 6; 10; 15]. Крутизна характеристики ошибки квантования для акселерометра, работающего в режиме автоколебаний, в среднем составляет 9 дБ/дек для заданного режима работы акселерометра. Разница в крутизне характеристики ошибки квантования объясняется самой сутью работы автоколебательного режима акселерометра – количеством тактовых импульсов, приходящихся на одно компенсирующее переключение, в котором учитывается ошибка квантования [8]. В автоколебательном акселерометре компенсация происходит значительно реже.

Внешний вид характеристики, показанной на Рисунке 8, по своей сути соответствует характеристике, показанной на Рисунке 4, что полностью подтверждает теоретические предположения, сделанные в процессе разработки методики по улучшению точностных параметров маятникового акселерометра.

Методика снижения погрешности автоколебательного акселерометра

Методика снижения погрешности автоколебательного акселерометра включает в себя следующие действия.

• 1.    Использование в качестве объекта модернизации маятникового акселерометра компенсационного типа.

• 2.    Включение маятникового акселерометра компенсационного типа в режим автоколебаний.

• 3.    Разработка устройства перекомпенсации входного воздействия для автоколебательного акселерометра.

• 4.    Использование режима перекомпенсации входного воздействия в автоколебательном режиме работы акселерометра.

• 5.    Оценка снижения шума квантования автоколебательного акселерометра, работающего в режиме сигма-дельта АЦП.

Указанная методика может быть использована для широкого круга измерительных приборов, в которых в качестве чувствительного элемента используется подвижная масса.

Заключение

Рассмотренная методика снижения погрешности измерения автоколебательного акселерометра позволяет обеспечить улучшение точностных характеристик инерциальных датчиков первичной информации бортового информационно-измерительного комплекса перспективных космических робототехнических комплексов, а также позволяет снизить стоимость готового изделия.

Введение сигнала перекомпенсации приводит к устранению погрешности преобразования аналоговой величины в цифровой код и снижению требований к тактовой частоты преобразователя до значения 30…50 МГц (и ниже), что позволит выполнить устройство преобразования временных интервалов на иетегральных микросхемах малой степени интеграции на программируемых логических интегральных схемах или базовых матричных кристаллах по технологиям, широко применяемым в технике на современном историческом этапе.