Методика создания и применения цифрового двойника мобильного транспортно-перегрузочного канатного комплекса

УДК 625.54, 625.57, 621.86                                

Funding information: the research is done with the financial support from the Grant of President of the Russian Federation no. МД-422.2020.8 for young Russian scientists — Doctors of Sciences.

Введение. Предложены концепции создания нового поколения канатных транспортных систем. К ним относятся городские пассажирские канатные транспортные системы на основе технологии «Канатное метро» [1, 2] и мобильные транспортно-перегрузочные канатные комплексы (МТПКК) [2–5]. Комплекс (рис. 1) представляет собой несколько базовых станций канатной дороги, оборудование которых смонтировано на мобильных шасси [2, 3].

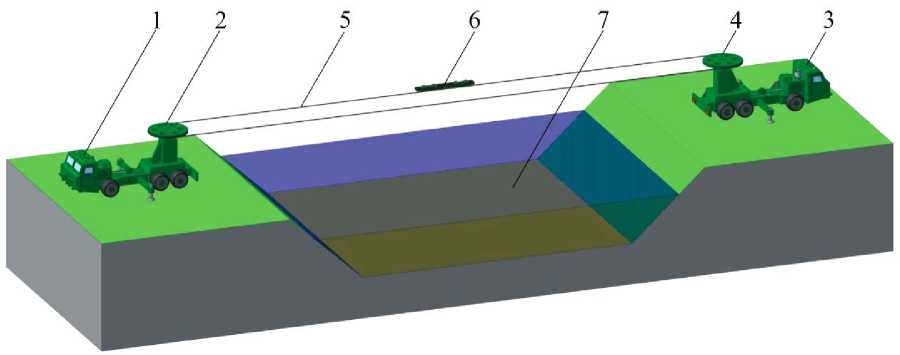
Рис. 1. Схема мобильного транспортно-перегрузочного канатного комплекса [2, 6]:

1 ― приводная базовая станция на основе колесного шасси; 2 ― приводной шкив; 3 ― неприводная базовая станция;

4 ― неприводной шкив с механизмом натяжения каната; 5 ― кольцевой тягово-приводной канат;

6 ― каретка для подвески груза; 7 ― преодолеваемое препятствие

Для успешной реализации данной идеи необходима разработка научных основ исследования рабочих процессов и проектирования МТПКК. При этом предстоит решить научно-технические задачи обеспечения общий устойчивости базовых станций, монтажа и натяжения канатной системы, погрузки и разгрузки канатной дороги [2].

В условиях цифровизации промышленного производства необходима разработка высокоточных цифровых двойников МТПКК, позволяющих создавать эффективные и конкурентоспособные в мировом масштабе образцы продукции.

Материалы и методы. Активная разработка системных цифровых моделей, которые можно считать прообразом цифровых двойников, началась с внедрением систем автоматизированного проектирования, поддерживающих основные этапы жизненного цикла промышленного изделия. Широко известна взаимосвязь этапов жизненного цикла и основных видов систем автоматизированного проектирования (рис. 2) [7].

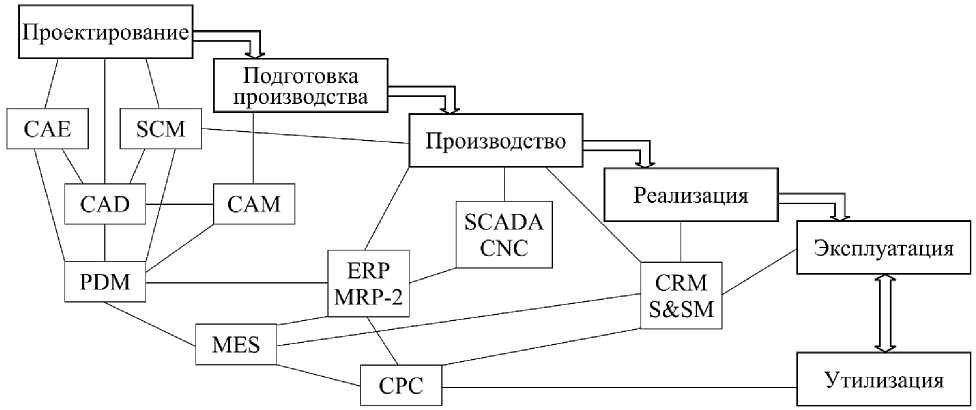
Рис. 2. Взаимосвязь этапов жизненного цикла промышленного изделия и основных систем автоматизированного проектирования

Анализ схемы (рис. 2) показывает, что существующие цифровые двойники промышленных изделий имеют наибольшую детализацию при использовании на этапах проектирования и производства. При этом рабочие процессы, протекающие на этапе эксплуатации промышленного изделия, учитываются при проектировании в виде исходных данных, представленных в виде числовых значений или законов распределения. В первую очередь к таким данным можно отнести внешние нагрузки и другие воздействия, последовательности рабочих операций. В рамках данного подхода [7] после изготовления промышленное изделие становится товаром, для которого в большей степени важны не технические, а экономические свойства: объемы продаж, цена, количество и характер претензий по гарантийному обслуживанию, отзывы покупателей, параметры документов купли-продажи. Поэтому на этапе эксплуатации разработанные в ходе проектирования и производства детализированные цифровые двойники, как правило, не используются. Они могут применяться при капитальном ремонте или модернизации промышленного изделия, однако в этом случае оно выводится из эксплуатации и возвращается на предприятие-изготовитель или специализированное ремонтное предприятие. Данный вывод также подтверждается тем, что 11 из 14 систем автоматизированного проектирования, представленных на рис. 2, связаны с проектированием и изготовлением.

Машиностроение и машиноведение

В условиях цифровизации промышленного производства такой подход является недостаточным, т. к. производитель промышленных изделий не обладает необходимыми данными для совершенствования конструкции, алгоритмов управления и технологии производства конкурентоспособной продукции, а потребитель не обладает полнотой информации об эксплуатируемом изделии. При этом активное внедрение цифровых двойников на этапе эксплуатации промышленного изделия позволит решить две основные задачи:

• —    эксплуатационная задача заключается в том, чтобы учесть возможные нештатные и аварийные режимы, которые нужно избегать в эксплуатации готового изделия;

• —    проектно-конструкторская задача ориентирована на создание новых конструкций и алгоритмов программного управления с учётом массива статистических данных и математических моделей, формируемых в ходе эксплуатации промышленных изделий.

Одновременно с этим важную роль играет постоянная актуализация цифрового двойника объекта, находящегося в эксплуатации. Таким образом, необходимо использовать разработанные высокоточные цифровые двойники на всех этапах жизненного цикла промышленного изделия [8, 9].

Для этого разработанные математические модели, лежащие в основе цифрового двойника, в режиме реального времени обрабатываются на быстродействующих компьютерах. В качестве исходных данных для расчета используются сигналы с датчиков, установленных на реальном объекте (рис. 3). Цифровой двойник связан с реальным объектом через облачный сервис. Такой подход позволяет повысить эффективность и безопасность эксплуатации промышленного изделия, выявить скрытые явления и эффекты, собрать материал для дальнейшей модернизации и повышения потребительских качеств, предотвратить аварийные ситуации [8, 9].

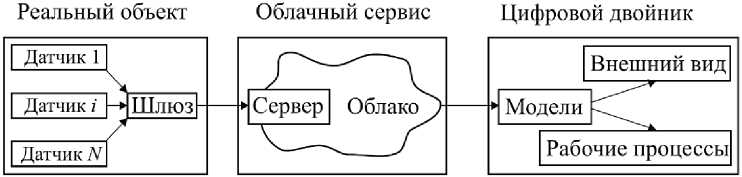
Рис. 3. Взаимосвязь промышленного изделия и его цифрового двойника

Таким образом, цифровой двойник ― это программный аналог физического устройства (промышленного изделия), моделирующий в режиме реального времени внутренние процессы, технические характеристики и поведение устройства в условиях влияния случайных воздействий и окружающей среды, параметры которых передаются с датчиков реального устройства, работающего параллельно [8, 9]. Цифровой двойник содержит в себе математические модели внешнего вида и рабочих процессов объекта. При этом размеры и характеристики внешнего вида используются для вычисления исходных параметров математических моделей, описывающих рабочие процессы. Например, момент инерции элемента механизма вычисляется на основе его геометрической модели. Затем полученное значение момента инерции транслируется в дифференциальное уравнение движения элемента.

Для построения математических моделей рабочих процессов промышленного изделия рекомендуется использовать системный подход [10], согласно которому каждому значащему элементу системы ставится в соответствие математическая подмодель, связанная с подмоделями других элементов с помощью совместных параметров и уравнений связи. Такой подход позволяет создавать удобные в использовании модульные математические модели, учитывать наличие обратных связей между элементами системы.

Данная статья посвящена созданию и использованию на этапе эксплуатации цифрового двойника мобильного транспортно-перегрузочного канатного комплекса. Другие этапы жизненного цикла МТПКК не рассматриваются, так как для них используются общие подходы, применяемые для любых машин и оборудования. Считается, что для разработки цифрового двойника имеются полные комплекты трехмерных компьютерных геометрических моделей МТПКК и конструкторско-технологической документации, разработанной на этапе проектирования и подготовки производства.

Рассмотрим варианты применения цифрового двойника для предотвращения аварийных ситуаций при эксплуатации мобильного транспортно-перегрузочного канатного комплекса. Пусть {a} — вектор параметров реального объекта, получаемых с помощью средств объективного контроля (датчиков, подключенных к измерительным системам). Эти параметры описывают текущее состояние МТПКК и характер протекающих рабочих процессов в текущий момент времени ti . Значения параметров {a} определяются периодически, через определенное время At. Параметрам, получаемым с физического объекта, соответствуют параметры {х}, вычисляемые с помощью математической модели. Результаты моделирования рабочих процессов записываются в матрицу [Х], которая содержит информацию об изменении моделируемых параметров во времени. Моделирование параметров выполняется различными пошаговыми численными методами, при этом величина шага вычисления по модельному времени tm равна Atm.

Параметры { a } в каждый текущий момент времени t_i передаются на вход математической модели, с помощью которой выполняется моделирование рабочих процессов МТПКК на заданный период времени T . Также при расчете используется информация о внешнем виде (конструкции) реального объекта. В результате расчета в режиме реального времени получаются значения [Х], по результатам анализа которых происходит оценка (прогноз) возможности наступления аварийной ситуации. Если по результатам моделирования прогнозируется наступление аварийной ситуации, то МТПКК немедленно останавливается или принимаются иные меры по предотвращению аварии.

Взаимосвязь реального объекта и цифрового двойника наглядно проиллюстрирована на рис. 4.

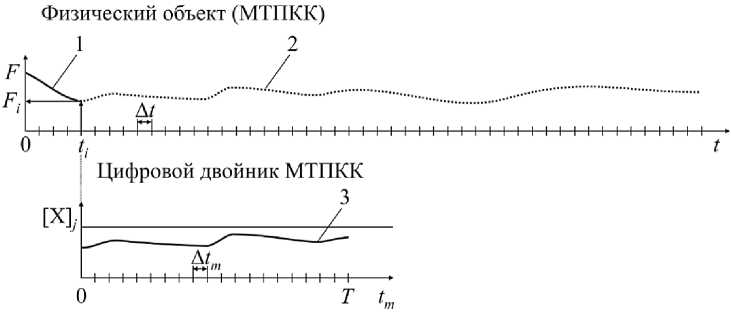
Рис. 4. Визуализация изменения рабочего процесса с помощью средств объективного контроля за реальным объектом и с помощью цифрового двойника: 1 — фактическое изменение параметра до момента t i ;

2 — фактическое изменение параметра реального объекта в будущем; 3 — результат моделирования изменения параметра в будущем с помощью цифрового двойника

Один из параметров вектора { a }, например сила натяжения несущего каната F, определяется с помощью силоизмерительного датчика с периодичностью A t . В текущий момент времени сила натяжения имеет значение F_i . Аналогичным образом определяются и другие компоненты a_i вектора { a }, которые передаются для анализа с помощью цифрового двойника.

Силе натяжения соответствует j -я строка матрицы [Х]. Если по результатам моделирования рабочих процессов МТПКК не выявлена возможность аварийной ситуации, то работа МТПКК не прекращается. На следующей итерации в момент времени t i + A t определяются новые значения вектора { a }, после чего выполняется новый сеанс моделирования. В случае негативного прогноза, например, если расчетная сила натяжения превысит допускаемое значение, то работа МТПКК прекращается до выяснения причин и устранения угрозы аварийной ситуации.

Для повышения точности прогноза необходимо использовать адекватные математические модели. Критерием точности может служить отклонение результата моделирования (участок 3 на рис. 4) от реального поведения объекта (участок 2 на рис. 4). В идеальном случае прогноз по изменению параметров должен полностью совпадать с фактическим изменением параметров в будущем.

В ходе исследования использовалась комплексная математическая модель, лежащая в основе цифрового двойника МТПКК [10]. Уравнения движения, входящие в эту модель, в общем виде можно записать следующим образом:

J[ M ]{^}+[ B ]{Х} + [ C ]{х} = { P},

[ [Y]={0}, где {х} — вектор законов движения элементов системы (изменения их координат во времени); {X} — вектор скоростей элементов системы; {X} — вектор ускорений элементов системы; [M] — матрица инерционных параметров, зависящая от масс и моментов инерции элементов системы; [B ] — матрица коэффициентов диссипации; [С] — матрица упругости, зависящая от жесткости элементов системы; {P} — вектор внешних нагрузок на элементы системы; [Y] — матрица алгебраических уравнений связи параметров системы:

Машиностроение и машиноведение

F_t = F ( { x } , { x } , { X } ) [10].

Рассмотренный подход позволяет спрогнозировать и предотвратить наступление аварийных ситуаций: — обрыв троса из-за превышения тягового усилия;

• —    сход каната со шкива;

• —    падение базовой станции из-за потери общей устойчивости;

• —    остановка привода канатной дороги с самораскачкой;

• —    отцепка кабины канатной дороги со скатыванием по канату и столкновением с другой кабиной или опорой;

• —    удар кабины об опору или оборудование базовой станции;

• —    сильная боковая качка при воздействии ветра.

Результаты исследования. Как было указано, цифровой двойник должен взаимодействовать с физическим объектом. Но мобильные транспортно-перегрузочные канатные комплексы являются перспективным видом транспортных систем, поэтому в настоящий момент их полноразмерные экспериментальные образцы отсутствуют. На данном этапе исследований для отработки методики создания цифрового двойника был создан масштабный натурный макет МТПКК, данные о работе которого передавались на вход цифрового двойника. Макет комплекса, изготовленный на базе Инжинирингового научнообразовательного центра цифровых технологий Индустрии 4.0 Брянского государственного университета имени академика И. Г. Петровского, представлен на рис. 5 .

В качестве контролируемого параметра выбрана координата точки подвеса груза z . Центр координат расположен на оси вращения приводного шкива, а ось координат соединяет центры шкивов канатной дороги. Текущее значение координаты на реальном объекте определялось с помощью программного обеспечения Kinovea, позволяющего анализировать данные видеосъемки.

рис. 6.

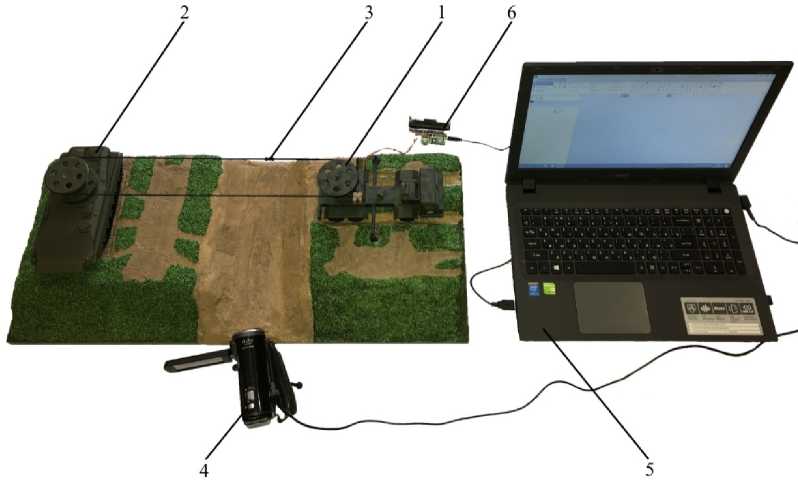
Рис. 5. Масштабный натурный макет МТПКК:

1 — приводная базовая станция; 2 — неприводная базовая станция; 3 — груз на подвеске; 4 — видеокамера; 5 — ноутбук для обработки сигналов и моделирования; 6 ― система управления макетом на базе микроконтроллера

Прогнозируемая координата точки подвеса груза вычислялась с помощью модели, представленной на

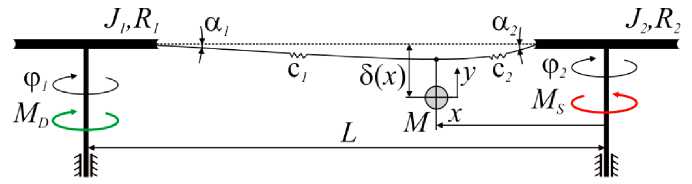
Рис. 6. Расчетная модель для исследования рабочих процессов макета

На стадии разгона канатной системы, когда скорость груза X меньше номинального значения ^х«_о м = 0,013 м/с, соответствующего установившемуся движению, уравнения движения элементов системы выглядят следующим образом:

J 1 Ф 1 + c И ^- —x —+ (^{S ( x} ) ^- у ) ^Sin ^{a L} I cos ^a i = ^m d ^{( ф} 1 ) ;

X     R 1 cos a              Ri J

I X                    ^si n а₂ I

J 2 ^ф 2 - c 2 | ^ф 2  --------+ (^{S ( X} ) ^- У ) I cos ^ф 2 = - M S ^{( ф} 2 )

X     R ₂ cos « ₂               R ₂ J

I _П , X              . х . I

MX - c₁ 1 R ₁ ф ₁-- + ( S ( x ) - y ) sin « ₁ I cos a -

( cos«J

<

Lx , X

- c ₂ 1 R ₂ ф ₂-- + ( S ( x ) - y ) sin « 2 I cos « 2 = 0;

• X       cos «2

I XI

My + c₁ 1 R ₁ ф ₁-- + ( S ( x ) - y ) sin « 1 I sin « 1 -

X       cos «i

X

• - c ₂ 1 R ₂ ф ₂-- + ( S ( x ) - y ) sin « ₂ I sin « 2 =- 9,81 M ,

(       cos «2

где ф ₁, J ₁ — угол поворота, момент инерции ведущего шкива соответственно; ф ₂, J ₂ — угол поворота, момент инерции ведомого шкива соответственно; x , y ― горизонтальная, вертикальная координаты груза соответственно; M ― масса груза; c ₁ и c ₂ ― жесткость каната в области приводного и неприводного шкива соответственно; « ₁ и « ₂ — угол наклона каната в области приводного и неприводного шкива соответственно; R ₁ и R ₂ ― радиус приводного и неприводного шкива соответственно; L ― расстояние между осями вращения шкивов (пролет канатной дороги).

Углы наклона ветвей каната:

« ₁ = « ₁ ( x ) = a sin J ^( x ) | при x * 0, « ₁ = 0 при x = 0;

X X J

« ₂ = « ₂( x ) = a sin J ^{( X} ) | при x * 0, « ₂ = 0 при x = L ,

X L - x J где зависимость стрелы прогиба каната от положения груза в пролете канатной дороги определена на натурном макете и имеет следующий вид:

S ( x ) = 0,003 sin( n x / L ) м.

Жесткости элементов макета определяются следующим образом:

c x 1 = c x 2 = ^{100 Н/м}; ^c 1 = c x 1 / ^R 1 ; c 2 = c x 2 / ^R 2 .

Далее приведем значения прочих параметров модели: J ₁ = J ₂ = 0 , 059 кгм; M = 0 , 025 кг; L = 0 , 395 м; R ₁ = R ₂ = 0 , 03 м; M D = 34,3-10 - 3 Нм; M S = 0,15-10 - 3 Нм.

Машиностроение и машиноведение

На стадии установившегося движения используется закон движения:

• ^X = ^X 0 ^{+ X} HOM t ,

где x ₀ — координата положения груза, соответствующая окончанию переходного процесса и началу установившегося движения.

На рис. 7 продемонстрирована реальная траектория движения точки подвеса груза и результаты ее моделирования с помощью цифрового двойника. В случае принудительной остановки канатной системы путем удержания груза происходило отклонение реального положения груза от прогнозируемого с использованием цифрового двойника. Этот факт фиксировался системой управления макета, при этом определялось отклонение е , что позволяло выявить аварийную ситуацию типа «буксование каната».

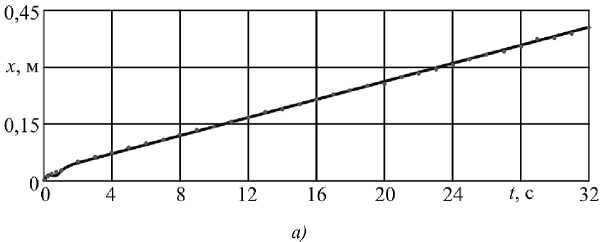
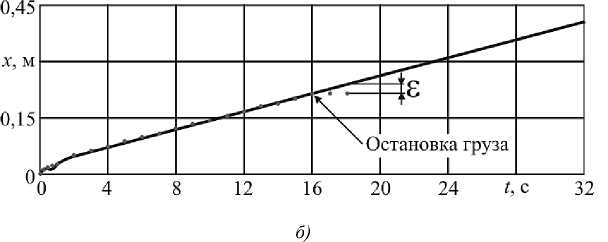
Рис. 7. Результаты моделирования с использованием цифрового двойника: а — нормальное движение; б — случай принудительной остановки каната; ― результат моделирования; ― экспериментальные значения

Обсуждение и заключения. Применение рассмотренной методологии создания цифровых двойников позволило на примере натурного макета канатной дороги выявлять отклонения от нормальной работы с целью предотвращения нештатных и аварийных ситуаций. В ходе дальнейших исследований на базе рассмотренной методологии будет создан промышленный цифровой двойник мобильного транспортно-перегрузочного канатного комплекса. При этом будут построены модели аварийных ситуаций.