Методика структурно-параметрической идентификации системы временных рядов

Одной из важных задач во многих отраслях промышленности является задача прогнозирования будущего состояния технического объекта. В большинстве случаев состояние объектов в различных технических приложениях характеризуется набором значений параметров, фиксируемых через определенные моменты времени и образующих систему временных рядов. При этом часто наблюдается высокая степень корреляционной зависимости между временными рядами значений параметров технического объекта. При моделировании динамики временных рядов нередко сталкиваются с такими нарушениями схем регрессионного анализа, как высокая степень автокорреляционной зависимости между последующими и предшествующими членами временного ряда, ненормальность распределения остатков и другие. В связи с этим возникает задача комплексной обработки системы взаимосвязанных временных рядов с обязательной проверкой соблюдения предположений нормальной схемы Гаусса-Маркова и последующей адаптацией к их нарушениям.

диагностика свойств остатков и при необходимости – адаптация к нарушениям предположений о характеристиках этих свойств.

Рассмотрим технический объект, состояние которого характеризуется параметрами, значения которых регистрируются через определенные промежутки времени и образуют систему временных рядов, которую можно записать в виде y ⁽ t ) = ^{ y ⁽ t 1 ), y ⁽ t 2 ), — ^, y ⁽ t n )} , где параметр t указывает на момент времени, в который зафиксировано значение, или номер наблюдения.

Пусть t = 1, 2, — , n (т.е. количество наблюдений равно n ), рассмотрим N временных рядов y 1 ( t ), y ²( t ), — , y^N ( t ) .

В соответствии с подходом адаптивного динамического регрессионного моделирования одномерный временной ряд y i (t) , наблюдаемый в равноотстоящие моменты времени 1 1 ,1 ₂,. — , t_n представляется в виде:

y i (t) = f i ( t ) + g^l( t ) + ^ '( t ) + ^ ( t ), (1) при этом функция f i (t) – неслучайная (долговременная) функция тренда соответствующего ряда; g i (t) – неслучайная периодическая функция – совместная гармоническая составляющая ряда; ^ (t) — случайная с элементами регулярности функция - векторная авторегрессия; E i (t) – нерегулярная компонента (случайная величина, ошибка).

На первом этапе для системы временных рядов выполняется разведочный анализ (фрактальный, мультифрактальный) для выявления степени регулярности каждого ряда системы [3].

При выявлении заметной трендоустойчиво-сти для соответствующих рядов выделяется функция тренда f(t) , которою обычно приближают полиномом достаточно низкой степени, также могут быть использованы и различные нелиней- ные по оцениваемым параметрам выражения. Оптимальная функция трендовой составляющей ищется по критерию минимума внешнего среднеквадратического отклонения (СКО) Гд .

Точность аппроксимации г (внутреннее

СКО) рассчитывается по формуле:

у которых на данном периоде T k имеются значимые гармоники.

Совместную гармоническую составляющую можно представить в виде:

E . Г 2Ш.

A k '^sin —

n /2

к = 1

V

T k

+ Ф к , 7

^г =_А 2 ⁽ у * ^{— y}i ^)2/( n ^— p ),

V i = 1

где n – количество наблюдений, p – число слагаемых в модели, y i - результат i -го наблюдения, y i - прогнозируемое значение по построенной модели.

Для вычисления внешних мер (внешнего СКО Г _д и др.) [1] исходная выборка данных делится на две части - обучающую и контрольную. По обучающей выборке строится модель, по контрольной – внешние меры, характеризующие прогностические свойства модели.

Точность прогнозирования Г _д вычисляется по формуле:

2л к где t = 1, 2,..., n, A := 2=1-----, Фк = Ф2к — Ф1 к kTk

Коэффициенты

А к , Ф jk ⁽ j = 1, ²,••■^, N , ^к = 1, ², , ⁿ ) находим для каждого из N временных рядов по формулам:

Ajk   д) w к + v к vjk

Ф кк = arctg ⁽---- ), w jk

k

Г _; 2 ( Д i -Д )²/( к - 1),

\ i = 1

где Д i = y i — y i , i = 1, к ( k - количество элементов контрольной выборки),

n w№=2£ d =1

trend jd

• sin

^ 2 n d

,

V ^тк 7

Д =

k

2 Д *

i = 1

k

y i – наблюдаемое значение отклика на контрольном интервале, y i - его прогноз - значения, вычисляемые по комплексной модели.

При этом для оценивания применяется линейный или нелинейный метод наименьших квадратов. Полученная модель для одного ряда может быть представлена в виде:

y i ( t ) = f ( t ) + £ _ trend* ( t ) ,       (5)

где y i ( t ) - фактические значения i -го ряда; f i ( t ) – функция трендовой составляющей для i -го ряда, £ trend ( t ) - случайная величина, характеризующая отклонения реального значения ряда от теоретического, найденного по уравнению регрессии.

Далее из каждого ряда системы выделяются остатки £ _ trend* ( t ) :

£ _ trend ( t ) = y ( t ) — f ( t ) .       (6)

Дальнейшее сглаживание временных рядов производится методами гармонического анализа, основанного на использовании формул Фурье.

Для каждого временного ряда методом пошаговой регрессии находятся значимые гармоники. Затем последовательно ищутся совместные амплитуды и фазы только для тех временных рядов,

v jk

n

= 2£ _ trendjd d =1

• cos

V

^2JT 1

^Тк 7

^{n к} к .

Далее находятся остатки для каждого временного ряда:

£ _ g i ( t ) = £ _ trend ( t ) — g i ( t ) .       (11)

После выделения регулярных составляющих целью анализа системы временных рядов является моделирование остатков £ g i ( t ) случайной с элементами регулярности функцией ^ (t) . Функция ^ (t) для системы взаимосвязанных временных рядов может быть представлена в виде модели векторной авторегрессии.

Модель векторной авторегрессии – это система уравнений, каждое из которых представляет собой модель авторегрессии и распределенного лага. Пусть x* (t) i = 1..N - i-й временной ряд. Модель векторной авторегресии порядкаp – модель для i-го временного ряда будет иметь вид xi( t) = a 0 + ]Ta ^jx-jX t — 1) + j=1

₊ ]T a _{2 j} x j ( t — 2) ₊ ... ₊           (12)

j = 1

+ ]T a Pj X ^j ( t — P ) + £ i ( t )

j = 1

Матричная запись модели векторной авторегрессии порядка p для системы временных рядов X ( t ) — { Х 1 (t ), X 2 ( t ), ..., X n ( t ) } запишется в виде

X ( t ) — a о + A_x X ( t — 1) + A 2 X ( t — 2) + ... +

p

^{+ A}p^{X (} t ^— P ) ^{+ E (} t ) ^— a 0 ⁺ E ^Am^{X (} t ^{— m} ) ^{+ E} t )

m — 1

где A m – матрицы элементов a mi j .

Коэффициенты уравнений модели можно получить методом наименьших квадратов, пользуясь следующей формулой:

A — ( X T X ) ^{— 1} X^TY .        (14)

Здесь X – это матрица значений рядов, представленная в виде:

1 x 1 (t - 1) . 1 x 1( t — 1) . ... - x 1(t — p) -- x1(t — p) • . xN (t — 1) . . xN (t — 1) . . xN (t — p) . xN (t — p) ,(15) V1 x 1( t — 1) . . x1 (t — p) .. . xN (t — 1) . . xN(t — p)у единичный столбец соответствует нулевому коэффициенту.

Y – вектор последних значений всех рядов:

В результате операций над матрицами, получаем матрицу коэффициентов A , имеющую (1+ N · p ) строк и N столбцов.

a ¹ ₀

v

a N • p

^N 0

N

N • p у

Каждый столбец здесь соответствует коэффициентам для i -ого уравнения модели.

Остатки e i g ( t ) после вычитания из исходного ряда регулярной составляющей представляются в виде модели векторной авторегрессии:

N e _ gi (t)— a о+ E a ij-yj(t— 1)+ j—i

+ £a '„yj (t " 2) + ...+ j—1

N

+ E a^y1 (t— p)+ j—1

p

⁺ E a k E _ g i ⁽ t ^{— k} ) ^{+ E} i ⁽ t ) k — 1

Оптимальная модель векторной авторегрессии (18) ищется по критерию минимума внешнего СКО Г _д , рассчитанного по формуле (3). Далее из каждого ряда системы выделяются остатки:

e ' ( t ) — E _ g i ( t ) — I a 0 + E a i,! t — 1) + E ( t — 2) + ■■■ + 1_ -t — P ) + ^ _ У• — k ) l .

V j = i                       j =i                               j = i                         k = i                         у

В итоге получаем для каждого из N временных рядов комплексную модель следующего вида:

^y i ⁽ t ) ^— f i ⁽ t ) ^{+ g}i ⁽ t ) ⁺ a 0 ⁺

NN

+ E aij yj (t — 1) + E a^У1 (t — 2) + ... + j—1

Np

⁺ E a^y' ⁽ t ^— p ) ⁺ E a ^{E _} g^{i (} t ^{— k} ) ^{+ E} i ⁽ t )

j — 1

Для построенных моделей по формулам (2) и (3) подсчитывается точность аппроксимации г и прогнозирования Г _д .

После структурно-параметрической идентификации системы временных рядов проверяется соблюдение условий применения “регрессионного анализа-метода наименьших квадратов”. Если основные предположения соблюдаются, построенная комплексная модель системы временных рядов может быть использована для прогнозирования.

При несоблюдении предположений проводится соответствующая процедура адаптации к нарушению данного предположения [1].

Ниже представлены результаты анализа, моделирования и прогнозирования временных рядов вибраций гидроагрегата в режиме работы в сети. Наблюдения в режиме работы агрегата в сети длились 1200 секунд, показания снимались 2 раза в секунду, всего получено 2400 наблюдений по каждому из восьми каналов. После усреднения каждые 10 секунд получилось 120 наблюдений.

Применяя методику структурно-параметрической идентификации системы временных рядов для моделирования измерений вибраций по восьми каналам, получены следующие модели:

y ¹(t) = 641 , 946 + 0 , 025 • t + 1 , 022 • sin ( — 26 , 68 • t + 65 , 093 ) + + 0 , 001 • y ² (t-1)- 0 , 001 • y ³ (t-1) — 0 , 002 ^ y ⁴ (t- 1 ) +

+ 0,001- y5 (t-1) + 0,0004^ y6 (t-1)-0,002^ y7 (t-1) + £1 (t), y2 (t) =698,017 — 0,003 • t +1,022 • sin(12,493 • t — 22,256) —

— 0 , 0002 - y ¹ (t- 1 )- 0 , 006 • y ³ (t- 1 ) + 0 , 007 • y ⁴ (t- 1 ) —

— 0,004 • y5 (t-1)-0,001 • y6 (t-1) + £2 (t), y3 (t)=225,93 + 0,997 • sin(0,0001 • t +11,456) —

— 0 , 317 • y ¹ (t- 1 ) + 0 , 002 • y ⁴ (t- 1 ) + 0 , 0001 • y ⁵ (t- 1 ) —

— 0,001 • y6 (t-1) + 0,011 • y7 (t-1) + 0,005 • y8 (t-1) + £3 (t), y4 (t)=44,752— 0,109-1 +1,021- sm(236654^ t +170546) +

+ 0 , 001 - y * (t- 1 ) + 0 , 0002- y ² (t- 1 ) + 0 , 008 ^ y ³ (t- 1 ) —

— 0 , 001 - y ⁵ (t- 1 ) + 0 , 002 ^ y ⁶ (t- 1 )-0, 014 ^ y ⁷ (t- 1 ) —

—0,007- y8 (t-1)+£4 (t), y5(t)=29,174 + 0,008 ■ t +1,023 ■ sin(-1,299 ■ t + 0,041)- 0,001 ■ y1 (t-1)-0,0001 ■ y2 (t-1) + 0,0001 ■ y3(t-1) -- 0,0003 ■ y6 (t-1) + 0,0002 ■ y8 (t-1) + e5 (t), y6 (t) = 3,943 ■ t + 1,014 ■ sin (- 0,191 ■ t + 2,518) +

+ 0 , 109 ■ y ¹ (t- 1 )- 0 , 001 ■ y ² (t- 1 ) - 0 , 199 ■ y ³ (t- 1 ) -

• -    0 , 024 ■ y ⁴ (t- 1 )- 0 , 002 ■ y ⁵ (t- 1 )- 0 , 129 ■ y ⁷ (t- 1 ) + e ⁶ (t),

y ⁷ (t) = 26 , 049 + 1 , 001 ■ sin ( 0 , 040 ■ t - 0 , 011 )

• -    0 , 001 ■ y ¹ (t- 1 ) + 0 , 001 ■ y ³ (t- 1 ) + 0 , 0002 ■ y ⁴ (t- 1 ) -

• -    0 , 001 ■ y ⁵ (t- 1 )- 0 , 001 ■ y ⁶ (t- 1 ) + 0 , 004 ■ y ⁸ (t- 1 ) + e ⁷ (t),

  y ⁸ (t)= 32 , 155 + 1 , 022 ■ sin ( - 3197 , 496 ■ t + 734 , 684 )

• -    0 , 0004 ■ y ¹ (t- 1 ) + 0 , 016 ■ y ³ (t- 1 ) - 0 , 008 ■ y ⁴ (t- 1 ) +

  + 0 , 0003 ■ y ⁵ (t- 1 ) + 0 , 0004 ■ y ⁶ (t- 1 )- 0 , 004 ■ y ⁷ (t- 1 ) + e ⁸ (t).

На рис. 1 а показаны графики исходных данных (сплошная линия) и аппроксимации по соответствующей модели (штриховая линия), а также графики (Рис. 1 б ) предсказанных (штриховая линия) и исходных (сплошная линия) значений временных рядов для данных вибраций по первому каналу.

Для сравнительного анализа эффективности разработанной методики моделирования системы временных рядов использовалась методика построения моделей авторегрессии проинтегрированного скользящего среднего (АРПСС), реализованная в пакете Statistica [4].

Построенные модели АРПСС в пакете Statistica, представлены ниже.

y1 (t)=643,6562+0,2151y1 (t-1), y2 (t)=697,9956-0,3888 ■ e2 (t-1)-0,1814 ■ e2 (t- 2 ), y3 (t)=21,16052+0,51052 ■ y3 (t-1), y4 (t)=39,69158-0,10275 ■ e4 (t-1)+0,20859 ■ e4 (t- 2 ), y5 (t)=28,76911-0,20671 ■ e5 (t-1)+ 0,12513 ■ e5 (t- 2 ), y6(t)=-42,3635+0,8185 ■ y6(t-1 )+0,1815 ■ y6(t-2) -- 0,0973 ■ e6 (t-1)+0,5629 ■ e6 (t- 2), y7 (t)=25,28663+0,96942 ■ y7 (t-1) +

+ 0,61375 ■ e7 (t-1)+0,22012 ■ e7 (t- 2 ), y8 (t)=31,82976-0,06093 ■ e8 (t-1).

Результаты сравнения по точности прогнозирования (внешнее СКО) двух методик для системы временных рядов, полученных по восьми каналам измерения вибраций в режиме работы в сети гидроагрегата, приведены в табл. 1.

Таким образом, совместное описание характеристик технического объекта с применением методики многоэтапной структурно-параметрической идентификации с адаптацией к нарушениям основных предположений регрессионного анализа повышает точность прогнозирования по сравнению с точностью при использовании одномерных методов (методика АРПСС), что позволяет принимать с определенным запасом времени управленческие решения, направленные на предупреждение опасной ситуации.

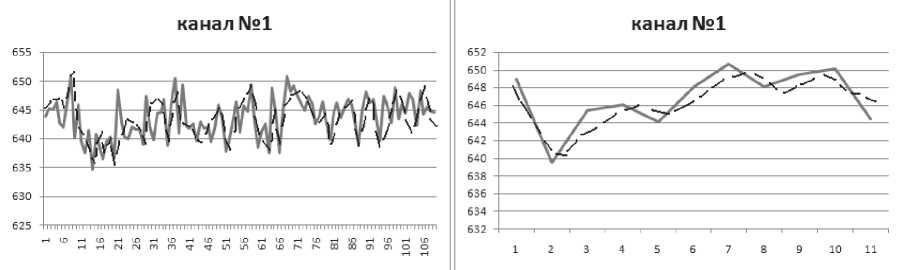
а

б

Рис. 1. Моделирование ( а ) и прогнозирование временного ряда ( б )

Таблица 1. Оценка точности прогнозирования для системы временных рядов при использовании двух методик

Номе р кан ала Методика	Среднеквадратическое отклонение прогнозирования ( ^ д )
	1	2	3	4	5	6	7	8
Методика АР ПСС (Statistica)	4,99	3,32	2,68	15,91	8,21	878,55	6,01	2,72
Методика ст рукт урно-па рам етри чес кой иде нт ифи каци и системы врем енн ых рядов	3,56	2,57	2,25	14,17	6,12	667,124	3,60	2,20

Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.B37.21.0672 (федеральная целевая программа “Научные и научно-педагогические кадры инновационной России”).