Методика учета стохастических факторов в имитационной модели роботизированной производственной ячейки

Современный этап развития промышленного производства неразрывно связан с концепцией Индустрии 4.0, ключевыми элементами которой являются цифровизация и широкое внедрение роботизированного оборудования в технологические процессы. Применение промышленных и кол-лаборативных роботов позволяет значительно повысить производительность труда, стабильность качества выпускаемой продукции и гибкость производственных линий, что особенно актуально для концепции Индустрии 4.0 [1]. Важнейшим этапом разработки сложных робототехнических комплексов (РТК) становится создание их цифровых двойников – комплексных виртуальных моделей, предназначенных для анализа, оптимизации и предиктивного обслуживания на всех этапах жизненного цикла.

Проектирование и ввод в эксплуатацию РТК представляют собой трудоёмкую и длительную задачу. Прямая отладка компоновочных решений и управляющих программ на физическом оборудовании сопряжена с риском его повреждения и значительными простоями. В таких условиях ключевым инструментом для инженеров становится имитационное моделирование (ИМ), позволяющее на виртуальном уровне провести анализ компоновки оборудования, проверить досягаемость рабочих зон, рассчитать циклограмму, выявить потенциальные коллизии и осуществить оффлайн-программирование задействованных роботов-манипуляторов [2].

Рис. 1. Деталь колеса компрессора МГТД

комплекса. Реальные производственные процессы, в свою очередь, неизбежно подвержены влиянию стохастических факторов, таких как внезапные отказы оборудования, вариативность времени выполнения технологических и вспомогательных операций, погрешности систем технического зрения и другие случайные события.

Объектом исследования в настоящей работе выступает роботизированная производственная ячейка (РПЯ), предназначенная для автоматизированного обслуживания фрезерного станка при обработке заготовок или постобработки после аддитивного производства сложнопрофильных деталей, таких как колесо компрессора (рис. 1) малоразмерного газотурбинного двигателя (МГТД).

Актуальность задачи связана с необходимостью синхронизации работы РПЯ в производственной цепочке серийного производства, объединенной общим ритмом и тактом выпуска. Существует ряд сложностей при реализации такой ячейки в виду вариабельности условий производства, например, обеспечение точной ориентации подаваемой в зону обработки заготовки, реализуемой с помощью системы технического зрения, определяющей угол поворота детали посредством детектирования лопаток.

Для выявления степени влияния подобных условий на работу РПЯ в рамках проекта по созданию киберфизической фабрики производства МГТД на базе Самарского университета была создана тестовая ячейка (рис. 2б). Ячейка включает мобильную роботизи рованную платформу REDS Education Pro с установленным на ней шестиосевым коллаборативным роботом REDS C20 и пятиосевым фрезерным обрабатывающим центром IMU-5X-300. Для данного комплекса ранее была разработана детерминированная имитационная модель (рис 2а), позволяющая осуществлять оффлайн-программирование и базовый анализ производительности [3, 4].

a)

б)

Рис. 2. а) Модель роботизированной ячейки; б) физическая реализация ячейки

Цель настоящей работы заключается в осуществлении перехода от детерминированной к стохастической имитационной модели роботизированной ячейки путем разработки и программной реализации соответствующих вероятностных модулей. Работа направлена на создание моделирующей среды, способной воспроизводить не только штатный технологический процесс, но и случайные отклонения от него, с целью получения статистически достоверной оценки производительности и надежности проектируемого РТК.

АНАЛИЗ И КЛАССИФИКАЦИЯ СТОХАСТИЧЕСКИХ ФАКТОРОВ

Для повышения достоверности имитационной модели необходимо перейти от детерминированного описания процессов к стохастическому [5]. Этот переход требует предварительного анализа и формализации потенциальных случайных событий, способных оказать влияние на общую производительность и стабильность работы роботизированной ячейки. В реальных производственных условиях такие события возникают непрерывно и могут быть обусловлены как физическим износом оборудования, так и внешними факторами или ошибками во взаимодействии компонентов системы.

Все стохастические факторы, характерные для роботизированных ячеек механической обработ- ки, можно систематизировать и разделить на несколько основных групп в зависимости от источника их возникновения. В рамках данного исследования предлагается следующая классификация:

• 1.    События, связанные с промышленным роботом: включают механические и электрические неисправности манипулятора, а также ошибки программного обеспечения контроллера.

• 2.    События, связанные с обрабатывающим станком: охватывают отказы ключевых узлов станка (шпиндель, система смены инструмента), поломку инструмента, а также ошибки системы ЧПУ.

• 3.    События, связанные с вспомогательными системами: относятся к сбоям в работе периферийного оборудования, такого как система технического зрения (СТЗ), накопители заготовок, системы подачи СОЖ и др.

• 4.    Внешние и системные события: включают перебои в электропитании, потерю сетевого соединения между компонентами ячейки, а также ошибки, связанные с человеческим фактором (например, несвоевременное пополнение склада заготовок оператором).

Для количественной оценки влияния стохастических факторов на производственный процесс была составлена таблица, обобщающая основные типы случайных событий. Значения частоты возникновения (на 10 000 циклов) и среднего времени восстановления (MTTR – Mean Time To Repair) носят обобщающий характер: они получены на основе анализа технической документации и отраслевой статистики. В дальнейшем планируется провести сбор эмпирических данных с реального оборудования для уточнения параметров модели [6]. Представленные значения используются в качестве предварительных входных данных для стохастического моделирования (табл. 1).

Для моделирования возникновения описанных событий в симуляционной среде целесообразно использовать метод Монте-Карло.

Метод Монте-Карло предполагает многократное проведение численных экспериментов для получения статистической оценки поведения системы. В контексте поставленной задачи каждый полный прогон имитационной модели (например, в течение 24-часовой смены) рассматривается как одно испытание.

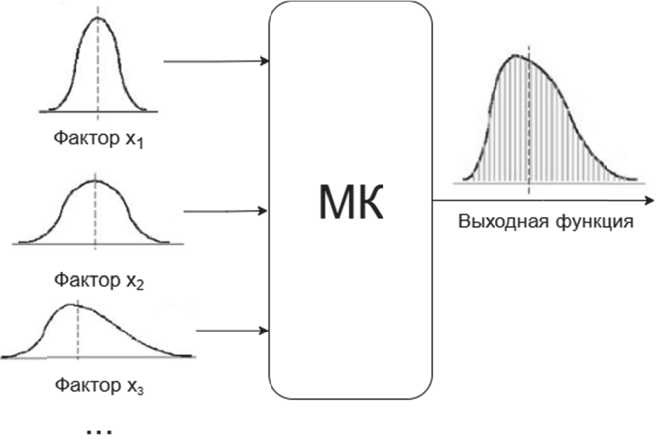
Рис. 3. Общая схема метода Монте-Карло

На рисунке 3 представлена общая схема реализации метода Монте-Карло. На вход имитационной модели f(x) подаются параметры x ₁, x ₂, x ₃, характеризующие стохастические свойства производственной системы. Эти параметры задаются в виде вероятностных распределений – нормального, экспоненциального, равномерного и других, отражающих реальную изменчивость входных условий: времени выполнения операций, вероятности отказов, длительности простоев и пр.

Алгоритм применения метода выглядит следующим образом: на каждой итерации основного цикла работы ячейки (или с заданной периодичностью) для каждого из N случайных событий генерируется псевдослучайное число r из равномерного распределения на интервале [0, 1]. Затем это число сравнивается с вероятностью Pi наступления i-го события. Вероятность Pi рассчитывается исходя из частоты, представленной в табл. 1. Например, вероятность отказа сервопривода сустава будет рассчитываться следующим образом:

V    2_

0.0002,

1 10000 10000

где V j - частота возникновения i-го события.

Если выполняется условие r < Pi, событие считается наступившим. В этом случае имитационная модель приостанавливает штатное выполнение технологического процесса и активирует процедуру устранения сбоя, длительность которой определяется значением MTTR. Время устранения также может быть задано не константой, а случайной величиной, подчиняющейся определенному закону распределения (например, нормальному или треугольному), что еще более повышает достоверность модели. Многократное проведение таких симуляционных прогонов позволяет получить распределение ключевых показателей эффективности и оценить их не только в идеальных, но и в реалистичных условиях эксплуатации.

Таблица 1. Классификация и параметры стохастических событий для РТК

№	Группа	Название события	Возможная причина	Влияние на процесс	Частота	MTTR
1.1	Робот	Отказ сервопривода сустава	Износ, перегрев	Полный останов робота, простой ячейки	2	120
1.2		Ошибка контроллера	Программный сбой	"Зависание" робота, требует перезагрузки	5	10
1.n		Потеря точности позиционирования	Нарушение калибровки, люфт	Брак детали, столкновение, простой	10	30
2.1	Станок	Поломка режущего инструмента	Износ, неправильные режимы резания	Останов станка, брак детали	50	15
2.2		Отказ системы смены инструмента	Механическое заклинивание	Останов станка в середине цикла	8	25
2.n		Сбой системы ЧПУ	Программная ошибка	Останов станка, потеря данных о цикле	5	15
3.1	СТЗ	Ошибка распознавания заготовки	Загрязнение оптики, плохое освещение	Увеличение времени цикла, простой ячейки	30	5
3.n		Некорректное определение координат	Блик на поверхности, сложная геометрия	Ошибка захвата роботом, столкновение	25	2
4.1	Внешние	Кратковременный сбой питания	Нестабильность электросети	Перезапуск всей ячейки, потеря прогресса	3	20

Одним из альтернативных методов стохастического анализа являются байесовские сети— вероятностные графовые модели, отображающие условные зависимости между событиями. Они позволяют обновлять оценки вероятностей на основе новых данных и находят широкое применение в диагностике, предиктивной аналитике [7] и интеллектуальных системах.

Однако для задач масштабного производственного моделирования байесовские сети обладают рядом ограничений: им присущ рост комбинаторной сложности, они требуют заранее заданной структуры зависимостей, чувствительны к качеству априорных данных и становятся вычислительно неэффективными при увеличении числа переменных. В результате что затрудняется адекватная инференция и прогнозирование. В отличие от сетей Байеса, метод Монте-Карло проще в реализации, лучше масштабируется и напрямую интегрируется в дискретно-событийную модель, что делает его более подходящим для анализа надёжности и устойчивости роботизированной производственной ячейки.

МЕТОДЫ РЕАЛИЗАЦИИ СТОХАСТИЧЕСКОЙ МОДЕЛИ

Симуляционная среда R-Pro предоставляет гибкие инструменты для учёта стохастических факторов при моделировании производственных процессов. В рамках разработанной модели роботизированной ячейки такие факторы реализуются двумя подходами: через штатную систему обработки отказов компонентов и программное расширение логики поведения объектов с помощью Python-скриптов [8].

Отказы станка моделируются с помощью встроенного функционала Failure, доступного для объектов с поведением ProcessExecutor (рис. 4). Через графический интерфейс пользователь задаёт параметры надёжности оборудования: MTBF, MTTR и закон распределения длительности ремонта (нормальный, экспоненциальный, треугольный, Вейбулла и др.). Этот механизм без программирования позволяет описывать типовые сценарии, такие как перегрузка шпинделя, сбой системы смены инструмента или ошибка обработки на уровне ЧПУ. Параметры надежности могут быть связаны с внешними источниками данных, например, Excel-таблицами, что позволяет оперативно адаптировать модель при изменении конфигурации оборудования без переписывания логики.

По умолчанию Failure

FailureMode      Cycles before failure                 T

CyclesBeforeFa... 0.000                          ГП

MTTR        0.000                 s Q

Automatic Repair 0

(^ Failure::MTTR

Распределение Постоянное Значение

I Значение Постоянное Значение

Нормальный Логарифмическое нормальное Равномерное Экспоненциальный

Гамма

Треугольная

Расп ределени Вейбулла

| Закрыть |]~О

Рис. 4. Учет вероятности отказов станка

В отличие от станка, робот, система технического зрения и периферийные устройства не имеют встроенного интерфейса отказов, поэтому моделирование случайных событий реализуется через пользовательские скрипты на языке Python, встроенные в логику компонентов. Проверка на отказ учитывается внутри функций, вызываемых при выполнении ключевых действий, например перед движением робота или попыткой захвата детали. Такие функции могут вызываться как напрямую из управляющей логики модели, так и через периодический опрос состояния и внешних сигналов.

На рисунке 5 приведён пример кода, моделирующего отказ привода одного из сочленений ма- нипулятора с заданной вероятностью.

1   free vcScript import •

2   import random

PJoint-fail - 0.0002

MTTRmean - 120

MTTRsigma • 36

ж Вероятность отказа на один цикл (2 на 10 000)

* Среднее время восстановления (мин)

ж Стандартное отклонение (30%)

def delay_sec(mean, sigma):

12 def OnRun():

13 comp ■ getComponent()

while True:

print("Отказ привода сустава! Остановка на ремонт.")

19                    ж Перевод состояния робота в аварийный режим

20                    comp.setProperty("State", "JointFault")

22                   delay_time - delay_sec(MTTR_mean, MTTRsigma)

23                   delay(delay_time)

25                   ж Восстановление работы

26                    print("Ремонт завершен. Возврат к работе.")

27                    comp. setProperty ("State", "Idle")

29           yield 0.1 ж проверка каждые 0.1 секунды

Рис. 5. Программный код, моделирующий отказ привода

В основе алгоритма лежит генератор random.random(), выполняющий проверку по схеме Бернулли. При каждом цикле моделирования происходит случайное «бросание кубика» с равномерным распределением на интервале [0, 1], и если полученное значение меньше порога P_joint_fail, инициируется событие отказа. Время восстановления (MTTR) моделируется с использованием функции random.gauss(), реализующей нормальное распределение.

Ошибки позиционирования также реализуются в виде вероятностных сценариев, которые учитывают сбои в системе технического зрения. При каждом вызове камеры происходит выбор одного из вариантов:

• .    с вероятностью p_fail система распознавания не находит объект;

• .    с вероятностью 1 – p_fail координаты центра объекта возвращаются, но с наложенной погрешностью, описываемой нормальным распределением δ ~N(0, σ ^2).

Также необходим учет накопления погрешности при позиционировании робота. Даже при отсутствии явных отказов в работе робота наблюдается постепенное снижение точности позиционирования вследствие механических люфтов и термической деформации [9, 10]. Для учёта этих факторов стандартные команды движения (например, move_joint() или move_linear()) оборачиваются функцией, добавляющей к целевым координатам небольшое случайное смещение. При этом амплитуда смещения увеличивается от смены к смене, отражая процесс деградации (рис. 6).

def degraded_target(x, у, z, n):

Рис. 6. Программный код, моделирующий накопление погрешности

Реализация таких сценариев позволяет оценить, через сколько часов или смен производственная точность выйдет за допустимые пределы и потребуется калибровка.

Представленные методы могут быть скомбинированы для создания комплексной стохастической модели, которая учитывает множество случайных факторов одновременно. Это позволяет проводить виртуальные испытания РТК в условиях, максимально приближенных к реальным, и получать статистически достоверные данные для анализа надежности и эффективности проектируемой системы. R-Pro предоставляет встроенный блок Statistics, автоматически собирающий данные о времени простоев, количестве отказов, длительности операций и других ключевых параметрах [11].

ЗАКЛЮЧЕНИЕ

В настоящей работе была решена задача повышения адекватности имитационного моделирования роботизированных технологических комплексов путем перехода от детерминированного подхода к стохастическому. Проведенное исследование позволило разработать методический подход, который систематизирует влияние случайных факторов на производственный процесс и предлагает конкретные способы их программной реализации в среде имитационного моделирования.

В ходе работы были достигнуты следующие ключевые результаты. Во-первых, была предложена и обоснована классификация стохастических событий, характерных для РТК механической обработки, с разделением их на четыре основные группы: связанные с роботом, станком, вспомогательными системами и внешними факторами. Для каждого типа событий были определены вероятностные параметры, такие как частота возникновения и среднее время на устранение, что формирует основу для количественного анализа рисков.

Во-вторых, в качестве теоретической базы для моделирования был выбран метод Монте-Карло, позволяющий путем многократных симуляционных экспериментов получать статистически достоверные оценки поведения системы в условиях неопределенности.

В-третьих, была продемонстрирована практическая реализуемость предложенного подхода на примере программного комплекса R-Pro. Разработаны и описаны конкретные алгоритмы на языке Python для моделирования таких событий, как поломка режущего инструмента, ошибки системы технического зрения и потеря точности позиционирования робота. Эти методы позволяют интегрировать вероятностные модели непосредственно в логику управления виртуальными компонентами.

Таким образом, предложенный инструментарий позволяет создавать имитационные модели, которые не только воспроизводят штатную циклограмму работы РТК, но и учитывают вероятностные сбои и отказы. Практическая реализация полученных результатов заключается в возможности на ранних этапах проектирования получать более реалистичные прогнозы по производительности, коэффициенту OEE и времени простоя оборудования. Это, в свою очередь, позволяет принимать более обоснованные решения по выбору компоновки, определению необходимого количества резервного инструмента, разработке графиков технического обслуживания и оценке экономической эффективности роботизации в целом.

Несмотря на достигнутые результаты, данное исследование имеет перспективы для дальнейшего развития. Остались неизученными вопросы автоматической оптимизации параметров ячейки (например, размера буферного накопителя) на основе данных стохастического моделирования. Кроме того, дальнейшим шагом является валидация разработанной модели путем сравнения результатов симуляции с эксплуатационными данными, полученными с реальной физической установки. Наиболее значимой перспективой является эволюция созданной модели до уровня полноценного цифрового двойника путем установления двусторонней связи с реальным РТК для сбора фактических данных о сбоях в реальном времени и автоматической адаптации вероятностных параметров модели.