Методика восстановления несущей частоты сигнала телеметрических систем при цифровой обработке

Контроль правильности отработки полетного задания бортовыми системами ракетоносителей (РН) и космических аппаратов (КА) осуществляется на основе обработки телеметрической информации (ТМИ) о состоянии большинства агрегатов и элементов объекта [1]. Для оптимального приема и обработки ТМИ, поступающей на наземные средства приема, необходимо восстановить несущую частоту радиосигнала и вычислить порог принятия решения для достоверного определения принимаемого символа информации (нуля или единицы).

В настоящее время в цифровых трактах приемных устройств для восстановления несущей радиосигнала с частотной манипуляцией чаще всего используются традиционные методы: быстрое преобразование Фурье (БПФ) или линейная фильтрация информационного параметра [2]. Применение БПФ требует большого количества производимых операций для получения необходимого результата и, следовательно, значительного времени для проведения анализа сигнала. А при линейной фильтрации весьма сложно получить несмещенную оценку обрабатываемого параметра. Кроме того, традиционные методы при обработке сигнала на фоне сильных шумов не позволяют достоверно определять несущую радиосигнала [3], что значительно сни- жает чувствительность цифровых радиоприемных трактов.

Методики и алгоритмы восстановления уровня несущей сигнала, альтернативные БПФ и методу линейной фильтрации, в настоящее время по-прежнему остаются слабо освещенными в отечественной и зарубежной литературе [4–6]. Поэтому разработка методики и алгоритма восстановления несущей радиосигнала на основе гистограммного метода, требующего проведения значительно меньших по сравнению с БПФ вычислительных затрат, является весьма актуальной.

Суть этого метода заключается в следующем. Диапазон возможных уровней сигнала на выходе частотного детектора разбивается на оптимальное число контрольных уровней, или интервалов. Сигнал после частотного детектора подается на блок построения гистограммы уровней. В этом блоке значения амплитуды сигнала сравниваются со значениями контрольных уровней, при этом фиксируется число попаданий значений амплитуды

A-A сигнала в интервал ∆k= kk-1 , где Akи Ak-1 – значения соседних контрольных уровней. Затем формируется одномерный вектор, т. е. вектор числа попаданий уровня сигнала в интервал «Δ(k) – гистограмма H(k). Параллель- но формируется вектор аккумуляторов S(к) или вектор суммы уровней сигнала в интервале А(к). По значениям гистограммы уровней сигнала определяются максимумы верхнего и нижнего уровней сигнала. На следующем шаге по значению максимумов H(к) и накопленному (аккумулированному) значению сигналов S(к) в максимумах вычисляется среднее значение верхнего (или нижнего) значения уровня сигнала.

Рассмотрим сигнал на выходе частотного детектора А ( t ) типичного двоичного приемника и соответствующую ему гистограмму (см. рисунок). Верхнему А 1 и нижнему А ₀ уровням сигнала на гистограмме Н ( к ) соответствуют два максимума. Значения максимумов зависят от количества единичных и нулевых символов в информационной посылке на интервале оценки. При равенстве количества единиц и нулей высота максимумов одинакова. При увеличении уровня шумов максимумы гистограммы сливаются в один, который соответствует распределению среднего уровня сигнала и шумов. Расстояние между максимумами определяется размахом сигнала. Середина расстояния ( А 1 + А ₀)/2 является уровнем несущей, зависящим только от расстройки частоты, и будет оптимальным порогом для решающего устройства, квантующего аналоговый сигнал частотного детектора на два уровня: единицу и нуль. Сигнал D ( t ) на выходе схемы принятия решения является бинарным образом сигнала А ( t ).

Количество единиц и нулей в информационной посылке в течение какого-либо периода может сильно различаться. Количественный максимум единиц (нулей), как показано на гистограмме справа, будет определять среднее текущее значение уровня сигнала единицы (нуля). Расстояние между уровнями сигнала гистограммных максимумов делится пополам и принимается за среднее значение уровня восстановленной несущей [6; 7].

Таким образом, методика восстановления уровня несущей гистограммным методом включает следующие этапы:

• 1)    определение интервала, на котором производится оценка уровней сигналов единиц и нулей. Установлено, что наилучший результат получается на интервале, совпадающем по длительности с интервалом накопления

значений сигнала для схемы автоподстройки частоты. Это связано с тем, что уровень сигнала на данном интервале минимально подвержен изменению;

• 2)    подсчет числа попаданий сигнала в контрольные интервалы и аккумулирование уровней текущего сигнала для каждого столбца гистограммы на интервале обработки;

• 3)    определение максимумов гистограммы и вычисление среднего текущего значения уровня несущей;

• 4)    восстановление принятого сигнала.

Основные характеристики данной методики следующие:

• -    обеспечение линейной зависимости оценки уровня несущей от расстройки;

• -    обеспечение несмещенной оценки среднего уровня несущей (ее значение не зависит от количества единиц и нулей в информационном сообщении);

• -    высокая устойчивость алгоритма восстановления уровня несущей, разработанного на основе этой методики, при высоком уровне шумов.

На основе предложенной методики построен следующий алгоритм.

На временном интервале, равном времени т _АП Ч , строится гистограмма H ( к ) выходных отсчетов частотного детектора. Количество диапазонов, или столбцов гистограммы к определяется необходимой точностью вычислений и однозначностью нахождения максимумов, соответствующих уровням передаваемых символов.

Параллельно вычисляются суммы S ( к ) по к диапазонам гистограммы. Далее производятся следующие операции:

• 1)    нахождение максимумов величин max₀ = H _{( к} mx. 0 . и max , = H _{( к} = _mx ) , соответствующих уровням нуля и единицы;

_А²⁾ оценка среднего уровня: А 0 = S ₍ mx₀) ^/ n (mx₀) и A 1 = ^S (mxi) / n (mxi) , где n ₍ mx₀) и n ₍ mx_{i )} - количество отчетов соответствующих уровней, и оценка среднего уровня несущей частоты, которая поступает на экстраполятор: ^A h = ( ^A 0 ^{+ A} i )^/2.

Введем обозначения: A _н = Y ( к ) - оценка уровня несущей в к -й момент времени; А Н = Y ( к + 1| к ) - выходное

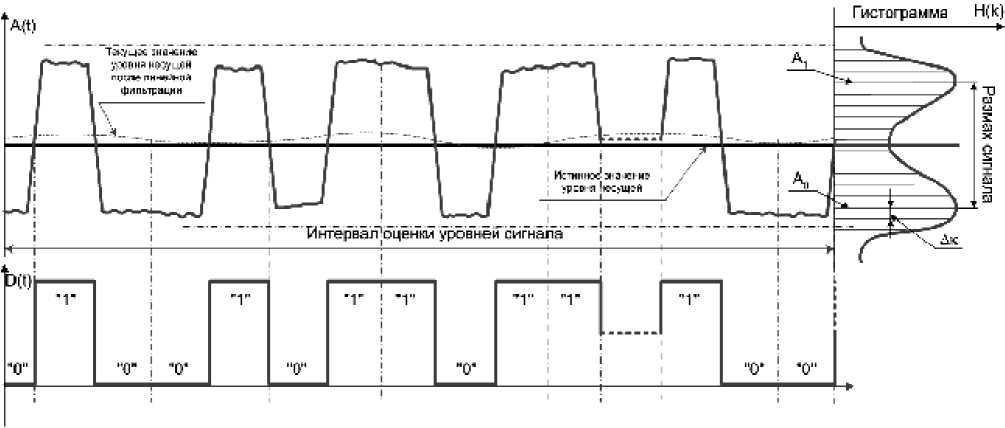
Сигнал на выходе частотного детектора и его гистограмма и восстановленный сигнал на выходе схемы принятия решения

значение экстраполятора, которое является оптимальным порогом для схемы принятия решения (эта схема квантует отсчеты частотного детектора на нулевые и единичные символы).

В общем случае экстраполятор описывается уравнением типа

Y(k + 1|k) = F [Y(k), Y(k -1),..., Y(k - (r -1))], где F – некоторая функция от r неизвестных; r – глубина памяти экстраполятора.

В устройстве слежения используются два экстрапо-лятора: линейный по двум точкам ( r = 2) и квадратичный по шести точкам ( r = 5):

Y (k + 1|k ) = 2 ■ Y (k)-Y (k -1),

Y ₂ ( k + 1| k ) =

= (9 ■ Y (k)-4 ■ Y (k - 2)-3 ■ Y (k - 4) + 3 ■ Y (k - 5))/5.

Для совместного предсказания линейной, квадратичной и других зависимостей параметра Y ( k ) результаты экстраполяторов объединяются:

Y: ( k + 1|k ) = £щг Y( k + 1|k), где должно выполняться соотношение ^ j aj = 1. Сумми рование проводится по всем j вариантам экстраполяции. Значения α j выводятся из минимума ошибки предсказания:

о2 [Yz (k +11 k)] = [^j ^ ■ Y (k +11 k) - Y(k +1)]2.

Для линейного и квадратичного экстраполирования

Y (k +1| k) = a, ■ Y (k +1| k) + a2 ■ Y2 (k +1| k), о2 [ Yz( k + 1|k )] =

= [a1 ■ Y (k + 1|k) + a2 ■ Y2 (k +1| k)-Y(k +1)]2.

Минимум этого выражения достигается при значениях коэффициентов a1 = о2 [Y2 (k +1| k)] /

/ (о2 [ Y (k + 1|k)] + о2 [ Y (k + 1|k)]), a2 = о2 [ Y (k +1| k)] /

/ ( о² [ Y ( k + 1| k ) ] + о² [ Y ₂ ( k + 1| k ) ] ) .

Следовательно,

M k + 1|k ) = о2 [ Y2 (k + 1|k )]■ Y1 (k + 1|k) + о2 [ Y1 (k + 1|k )]■ Y2 (k + 1|k) =              о2 [ Y1 (k + 1|k)] + о2 [ Y2 (k + 1|k)]              ’

С использованием доверительного веса выходное значение предсказанного параметра вычисляется по формуле

YBых (k + 1|k) = [1 - W(k)]■ Yz(k + 1|k) + W(k)■ Y(k), где доверительный вес нормирован так, что 0 < W (k) < 1. Следовательно, если доверительный вес высок, т. е. условия слежения нормальные, то предсказывающее устрой- ство более полагается на текущее значение параметра Y (k), в противном случае происходит предсказание параметра по тем его значениям, которые он принимал до уменьшения доверительного веса. Экспериментальные данные показали, что характеристики данного метода предсказания аналогичны калмановской фильтрации.

Результаты применения предложенного методического аппарата можно сформулировать следующим образом:

– разработаны методика и алгоритм восстановления среднего значения уровня несущей частотно-манипули-рованного сигнала гистограммным методом после частотного детектора без использования БПФ или линейной фильтрации информационного параметра, что обеспечивает более высокие быстродействие и помехоустойчивость;

– проведена оценка работоспособности разработанных методики и алгоритма на реальной информации, которая показала значительное сокращение числа проводимых вычислительных операций при восстановлении среднего значения несущей сигнала и устойчивость алгоритма к шумам. Зависимость A = ( А / ) от расстройки несущей А f является линейной;

– оценка уровня несущей сигнала не зависит от количества нулевых и единичных символов в передаваемой информации и не требует введения специальных посылок или маркеров для ее точного определения. Методика и алгоритм позволяют получить несмещенную оценку среднего уровня сигнала после частотного детектора при отклонении несущей частоты.

Таким образом, методика и алгоритм восстановления несущей частоты показали устойчивость, линейность и точность предложенного гистограммного метода оценки уровня несущей частоты и порога для принятия решения о значении принимаемого символа.