Методика выбора конфигурации наземных базовых станций локальной навигационной системы для обеспечения наименьшей погрешности навигационных определений

В настоящее время локальные навигационные системы (ЛНС) активно применяются для навигационно-временного обеспечения наземных и воздушных объектов в условиях отсутствия сигналов глобальных навигационных спутниковых систем (ГНСС) по различным причинам (городская застройка, горная местность, применение противником или своими войсками средств радиоэлектронной борьбы).

Размещение наземных базовых станций (НБС), которые являются элементами ЛНС, зависит от многих взаимозависимых параметров, таких как энергетический потенциал НБС, особенности рельефа местности на трассах «НБС-навигационная аппаратура потребителей (НАП)», требуемый размер зоны действия ЛНС, размеры зоны, в которой возможно размещение НБС, дальность прямой радиовидимости от НБС до НАП, ослабление сигналов ЛНС на трассе распространения радиоволн (РРВ) «НБС-НАП» [1]. Существующие методики [2, 3] не учитывают все возможные варианты расстановки НБС в зоне их размещения, не учитывают рельеф местности и дальность прямой радиовидимости. Поэтому задача по разработке методики выбора конфигурации наземных базовых станций локальной навигационной системы для улучшения точности определения координат НАП является особенно актуальной.

Цель работы – разработка методики выбора конфигурации НБС ЛНС для повышения эффективности применения НАП за счет уменьшения погрешности определения координат в условиях отсутствия сигналов ГНСС.

С целью удобства восприятия дальнейшего материала введём следующие определения:

– зона действия ЛНС – участок местности, в любой точке которого одновременно присутствуют сигналы минимум от трёх НБС, с уровнем мощности, позволяющим принять их в НАП;

– зона расположения НБС – участок местности, на котором имеется возможность разместить и обеспечить непрерывную работу всех НБС из состава ЛНС;

– геометрический фактор (ГФ) является количественной оценкой влияния взаимного расположения НБС на точность определения координат НАП в зоне действия ЛНС. Геометрический фактор показывает, во сколько раз ухудшится точность определения координат НАП в зоне действия ЛНС при заданной расстановке НБС. Данное ухудшение точности определения координат происходит на этапе вторичной обработки информации в НАП [4]. При этом для оценки точности определения горизонтальных координат используется значение горизонтального ГФ [2, 3]. Значение ГФ, превышающее единицу, характеризует ухудшение точности определения координат в НАП [5];

– среднеарифметическое значение геометрического фактора зоны действия ЛНС рассчитывается путем вычисления значения геометрического фактора для каждого участка местности из зоны действия ЛНС, последующего сложения значений геометрического фактора данных участков местности из зоны действия ЛНС и вычисления частного от количества участков местности из зоны действия ЛНС.

В качестве показателя эффективности размещения элементов локальной навигационной системы предлагается использовать наименьшее значение геометрического фактора [6]. Данный показатель является комплексным, так как учитывает, а следовательно, позволяет проводить детальный анализ влияния таких характеристик, как дальность прямой видимости, – 776 – энергетическая доступность, неперекрытие сигнала от НБС до НАП рельефом местности, на эффективность разворачиваемой ЛНС.

Расчет геометрического фактора и выбор конфигурации НБС с минимальным значением геометрического фактора осуществляется путем последовательного решения следующих частных задач:

• 1)    разбиение зоны действия ЛНС и зоны расположения НБС на отдельные точки;

• 2)    определение точек из зоны расположения НБС, пригодных для размещения НБС;

• 3)    составление всех возможных конфигураций (вариантов размещения) НБС с учетом их количества;

• 4)    расчет для составленных конфигураций НБС среднеарифметического значения геометрического фактора в зоне действия ЛНС;

• 5)    выбор конфигурации НБС с наименьшим среднеарифметическим значением геометрического фактора в зоне действия ЛНС.

Разбиение зоны действия ЛНСи зоны расположения НБС на отдельные точки

Зона расположения НБС разбивается на отдельные точки, расстояние между которыми по горизонтальной оси равняется величине Δ x , а по вертельной оси – величине Δ y . Общее количество точек рассчитывается по следующей формуле:

где N – количество точек в зоне; X – ширина зоны (м); Y – длина зоны (м); Δ x – расстояние между точками по горизонтальной оси (м); Δ y – расстояние между точками по вертельной оси (м).

Общее количество конфигураций НБС в комбинаторике называется комбинациями размещений из n объектов по k и рассчитывается по формуле:

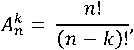
где n – количество точек в зоне, k – количество НБС из состава ЛНС.

Далее точки в зоне расположения НБС будут обозначатся как i- ая.

С учетом возможности современных процессоров количество точек в зоне расположения НБС не должно превышать 20. Если расстояние между точками по горизонтальной и вертикальной оси будет неприемлемым, предлагается последовательно выполнять приведенную методику, масштабируя зону расположения НБС.

Зона действия ЛНС разбивается на отдельные точки аналогичным способом, и общее количество точек должно быть таким же, как и для зоны расположения НБС.

Далее точка в зоне действия ЛНС будет обозначатся как j- ая.

Определение точек из зоны расположения НБС, пригодных для обеспечения зоны действия ЛНС

Точка является пригодной для расположения НБС только при одновременном выполнении следующих условий:

• –    обеспечение прямой радиовидимости от точки в зоне расположения НБС до каждой точки зоны действия ЛНС;

• –    обеспечение энергетической (электромагнитной) доступности навигационных сигналов от точки в зоне расположения НБС до каждой точки зоны действия ЛНС;

• –    обеспечение условия неперекрытия навигационного сигнала от НБС до ЛНС особенностями рельефа местности.

Расстояние прямой радиовидимости i- ой НБС с j- ой ЛНС определяется в соответствии со следующим выражением:

йпрО'М = 4,12 ■ ^VziHBcM + ^улнсМ).                        (3)

где D _{пр i} j – расстояние прямой видимости; z_{i НБС} – высота участка из зоны расположения НБС [м]; z j ЛНС – высота участка из зоны действия ЛНС [м] с учетом поднятия антенны.

Далее рассчитывается расстояние между участками из зоны расположения НБС и участками из зоны действия ЛНС:

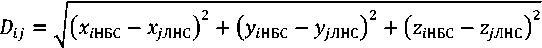
где xiНБС, yiНБС – координаты i-го участка местности из зоны расположения НБС; xjЛНС, yjЛНС – координаты j-го участка из зоны действия ЛНС, и проверяется условие (неравенство):

^ij < ^npij

Если условие (5) выполняется, то обеспечение прямой радиовидимости НБС с ЛНС для i -го участка из зоны расположения НБС считается выполненным.

Энергетическая (электромагнитная) доступность навигационных сигналов от точки в зоне расположения НБС до каждой точки зоны действия НАП проверяется следующим образом.

Рассчитывается мощность навигационных сигналов в точке из зоны действия ЛНС от всех участков из зоны расположения НБС, при этом значение мощности сигнала P СВХ от i -го участка из зоны расположения НБС определяется как:

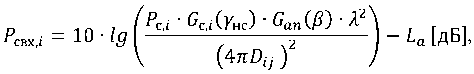
где P_ci – излучаемая мощность НБС [Вт]; λ – длина волны сигнала [м]; G_ci ( γ _нс) – зависимость коэффициента усиления антенны передатчика j -ой НБС в вертикальной плоскости от угла γ нс ; L_a j – затухание сигнала НБС в атмосфере [дБ].

Зависимость коэффициента усиления антенны НАП ЛНС в вертикальной плоскости от угла места (наблюдения) НБС определяется как:

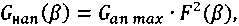
где G an ( β ) – зависимость коэффициента усиления антенны НАП ЛНС в вертикальной плоскости от угла места [раз]; G_{an max} – коэффициент усиления антенны НАП ЛНС в максимуме ДН [раз].

Форма главного лепестка нормированной ДН по мощности типовой антенны НАП ЛНС аппроксимируется выражением:

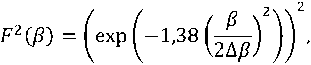
где β – угол места прихода сигнала от НБС; 2Δ β – ширина ДН антенны типовой АП.

Далее сравниваются значения P _{СВХ, i} с чувствительностью НАП ЛНС [7]. Если P _{СВХ, i} входит в диапазон чувствительности НАП ЛНС, то условие энергетической доступности для i -ой точки из зоны расположения НБС считается выполненным.

Обеспечение условия неперекрытия навигационного сигнала на трассе «НБС-НАП» особенностями рельефа местности рассчитывается путём построения профиля местности от зоны действия ЛНС.

Составление всех возможных конфигураций (вариантов размещения) НБС

Далее составляются все возможные варианты конфигурации НБС из доступных точек в зоне расположения НБС. На рис. 1 приведен пример конфигураций НБС. Черным цветом отмечена зона расположения НБС, белым – зона действия ЛНС. В данном примере конфигурации из 3 НБС составляются из 6 возможных для размещения точек.

После составления всех возможных вариантов конфигураций НБС в соответствии с выбранным показателем эффективности рассчитывается среднеарифметическое значение геометрического фактора в зоне действия ЛНС.

an	821	831	841	851	861	871	881	891	8io 1
812	822	832	842	852	862	872	882	892	810 2
313	823	8зз	843	853	863	873	883	893	8io 3
314	824	834	844	854	864	874	884	894	810 4
815	825	835	845	855	865	875	885	895	810 5
816	826	836	846	856	866	876	886	896	8io 6
		**—			«-»—	-»—	^—

Рис. 1. Пример составления возможных конфигураций НБС

Fig. 1. Example of drawing up possible configurations of the ground base station

Расчет для составленных конфигураций НБС среднеарифметического значения геометрического фактора в зоне действия ЛНС

Для каждой точки в зоне ЛНС рассчитывается значение геометрического фактора для сформированных конфигураций НБС следующим образом [8]:

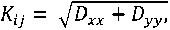
где D xx , D yy , D zz – первые три диагональных элемента квадратной четырехмерной матрицы D:

		Dxx Dxy Dxz Dxb
D =		Dyx Dy у Dy z Dyb
		ZX    zyivzz    zb
		^bx ^by^bz ^bb

D = (H^T ■ И)"¹,                                                        (11)

где H – матрица направляющих косинусов.

Матрица направляющих косинусов H вычисляется по формуле:

Н =

—cos(a1)

—cos(a2)

—cos(ctN)

-cosCpy-cosCyJ

-cos(/?2)-cos(y2)

-cos(pN)-cos(yN)

где α ₁, β ₁, γ ₁ – угол места прихода сигнала от НБС; K – количество видимых потребителем НБС. Направляющие косинусы определяются соотношениями:

xt — X, cos^ad = ——

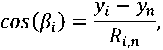
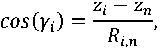
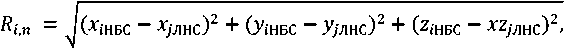
где x i НБС , y i НБС , z i НБС – координаты i-ой НБС, x i НБС , y П , z П – координаты НАП.

Далее вычисленные значения геометрического фактора для каждой точки из зоны действия ЛНС складываются и делятся на количество точек из зоны действия ЛНС. Среднеарифметическое значение геометрического фактора и i -я конфигурация НБС сохраняются.

Выбор конфигурации НБС с наименьшим средним значением геометрического фактора в зоне действия ЛНС

На данном шаге производится выбор минимального среднеарифметического значения геометрического фактора. Соответствующая данному значению конфигурация НБС является искомой.

Исходные данные, используемые в методике, и их принятые значения при проведении контрольных расчетов:

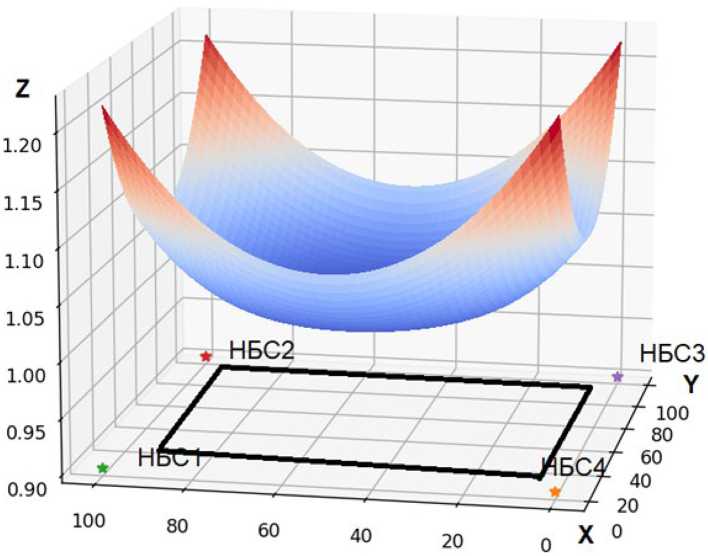
Рис. 2. Трехмерный график значений геометрического фактора в зоне действия ЛНС для конфигурации НБС

Fig. 2. Three-dimensional graph of the geometric factor values in the area of the local navigation system for the configuration of ground base stations

• –    количество НБС, (n);

• –    диапазон чувствительности НАП ЛНС, [дБВт];

• –    координаты зоны действия ЛНС (набор координатных точек в пространстве), ограниченные параметрами ( x i , y i , z i );

• –    координаты зоны расположения НБС (в данном случае набор координатных точек на плоскости) ( x i , y i , z i );

• –    рабочая частота ЛНС [MГц];

• –    энергопотенциал НБС [Вт];

• –    данные с цифровой матрицы высот местности, (м).

В качестве примера на рис. 2 представлены отдельные результаты контрольных расчетов в виде трёхмерного графика, на котором на оси Z отложено значение геометрического фактора для конфигурации из четырех НБС, равномерно распределенных по оси X , Y – условные координаты местности. Расчеты выполнены с использованием компьютерной модели для ЭВМ [8], реализующей данную методику расчета показателя эффективности – среднего значения геометрического фактора для i -ой конфигурации, которое для заданных условий составило 1,095.

Таким образом, представленная методика позволяет найти наилучшее взаимнопространственное расположение НБС относительно зоны действия ЛНС по критерию минимума среднеарифметического значения геометрического фактора. Универсальность представленной методики показывает её применимость к любому из перечисленных вариантов расположения ЛНС для обеспечения навигации любого типа НАП.