Методика выбора маховичных накопителей энергии в качестве источника автономного питания

Цитирование: Блинников, М. Е. Методика выбора маховичных накопителей энергии в качестве источника автономного питания / М. Е. Блинников // Журн. Сиб. федер. ун-та. Техника и технологии, 2022, 15(6). С. 691–701. DOI: 10.17516/1999-494X-0426

Если рассматриваемый накопитель рассчитан на использование, которое не меньше требуемого времени автономной работы (в режиме разряда), то рассматривается параллельная работа накопителей. Такие условия выбора имеют два вида.

• 1.    Выбор числа накопителей по ёмкости, шт.:

W

• ^/?МНЭ - ^,?МНЭ - ~         { оСнП ’                        ⁽¹⁾

• 2.    Выбор числа накопителей по мощности, шт.:

"МНЭ 'раб V7смр + 7 МНЭ / где nМНЭ - минимальное требуемое количество накопителей (целое число), шт.; ^НЭ — расчётное требуемое количество накопителей, шт.; Wp – расчётный запас энергии, потребляемый нагрузкой, которая будет выделяться на автономную работу от маховичного накопителя в течение заданного времени, кВт∙ч; WМНЭ – номинальная, располагаемая, гарантированная или другая величина ёмкости маховичного накопителя, на которую рассчитан накопитель по данным завода-изготовителя, кВт^ч; Рмнэ — мощность системы собственных нужд одного маховичного накопителя энергии, кВт; pсмр - удельный часовой саморазряд маховичного накопителя (может быть представлен средней величиной pсмр.ср или зависимостью от времени разряда pCмP(t), кВт); tраб - время работы маховичного накопителя в режиме разряда, ч.

р -и рСН

„           _ Р МНЭ                                       z~

• ^/?МНЭ - ^? МНЭ Р ■                                         ⁽²⁾

7 МНЭ где PМНЭ – выходная мощность накопителя, соответствующая требуемому времени работы, кВт; Pр – расчётная мощность нагрузки, подключаемой к накопителю, кВт.

Из двух условий (1) и (2) выбирается большее значение n _МНЭ, удовлетворяющее обоим условиям.

При последовательной работе накопителей, когда разряд осуществляется ступенями, каждая ступень должна не только питать целевого потребителя, но и поддерживать полный заряд остальных ступеней, которым только предстоит включиться в работу. Такую систему питания назовём каскадной.

Упрощённо представив характеристики саморазряда накопителей и мощность потребления целевой нагрузки средними значениями, получим выражение энергии, потребляемой на i -ой ступени питания, кВт∙ч:

где Pнг - мощность нагрузки целевого потребителя при работе i-ой ступени, кВт; Арсмз.ср - среднее значение мощности потерь от саморазряда маховичного накопителя (величина среднего часового саморазряда), кВт; А/^^р - среднее значение потерь, определяющее мощность, необходимую на поддержание полного заряда маховичного накопителя, кВт; nМНЭi – количество маховичных накопителей в i-ой ступени питания, шт; /,мнэ - количество маховичных нако-J                             под,- пителей, поддерживаемых в полностью заряженном состоянии i-ой ступенью питания, шт.; ∆ti – продолжительность работы i-ой ступени питания, ч.

Без учёта подпитки каждой ступени от накопителей предыдущей ступени выражение для источников имеет вид, кВт·ч:

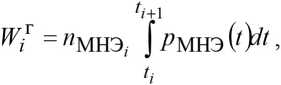
где n МНЭ i - количество маховичных накопителей в i -ой ступени питания, шт; p _МНЭ( / ) - зависимость выходной мощности накопителя от времени работы, кВт.

Зависимость выходной мощности p _МНЭ( / ) является экспериментальной кривой, которую производитель может прикладывать к техническим данным накопителя. Для выполнения расчётов кривую нужно заменить приближённой аналитической с точностью, определяемой необходимостью конкретной задачи.

Приближённое количество накопителей для каскадной схемы можно оценить следующим образом, шт.:

прибл ____________ Р ___________

"МНЭ         /МНЭ

МНЭ " 'раб.макс^МНЭ где /рдд макс - наибольшее время работы накопителя в режиме отбора мощности, ч; ApМНЭ -потери мощности в электромаховичном накопителе в целом, среднее значение, может быть использована средняя величина потерь от саморазряда, собственные нужды накопителя, например, мощность вакуумного насоса, подвеса, потери в моторе-генераторе, кВт.

Примеры применения методики выбора электромаховичных накопителей

Выберем накопитель располагаемой ёмкостью 30 кВт∙ч с наибольшим временем работы 35 минут на минимальной выходной мощности 50 кВт [1]. Примем следующие данные для расчёта: p смз.ср = 9 кВт,         = 3 кВт. Значение         принято по данным завода-изготовителя

[1], а значение p _смз . _ср ориентировочно увеличено в три раза из следующих соображений. Рассматриваемые потери складываются из потерь в электромеханическом преобразователе, потерь в электропреобразовательных устройствах (выпрямитель, фильтр, инвертор), а также вспомогательных устройствах управления и контроля. Потери на поддержание характерны работе электромеханического преобразователя МНЭ в качестве двигателя, электромагнитный момент которого уравновешивает момент сопротивления маховика. При этом двигатель работает в режиме, близком к холостому ходу. При разряде имеет место генераторный режим работы электрической машины, в котором ток нагрузки определяется работой на целевого потребителя, что обусловливает рост переменных потерь в электрической машине и электропреобразова-тельных устройствах.

В качестве объекта исследования рассмотрим систему собственных нужд электрической подстанции с усреднённой мощностью нагрузки 170,8 кВт. Минимальное время работы системы в автономном режиме составляет 2 часа [3]. С учётом коэффициента запаса 1,3 необходимый запас энергии составит 444,1 кВт∙ч. Так как время работы накопителя меньше требуемого времени автономной работы, используем расчёт для каскадной схемы питания.

Выберем возможное количество ступеней каскадной системы питания, то есть 4. Это количество является минимальным, потому что наибольшее время работы накопителя составляет 35 минут. Задачу выбора времени работы каждой ступени и количества накопителей на каждой – 694 – ступени удобно рассматривать как задачу оптимизации. Для создания математической модели задачи оптимизации необходимо определить целевую функцию, содержащую критерий оптимальности, граничные условия и ограничения [4, 5, 6].

Целевой функцией, подлежащей максимизации, является КПД системы за полуцикл разряда, то есть за время автономной работы, о.е.:

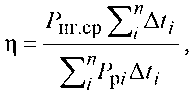
где P _р i - расчётная мощность нагрузки i -ой ступени, кВт; P _нг . _ср - усреднённая мощность по расчётному объёму энергии (поясним позже), кВт; ∆ t_i – продолжительность работы i -ой ступени, ч; i – номер ступени, о.е.; n – количество ступеней, шт.

Поскольку оптимизации подлежит только один критерий, поставленная задача является однокритериальной.

Граничные условия имеют вид:

А/, > О, _д МНЭ i - раб.макс’

ЙМНЭ, - °’ ^МИЭ, -целое.

Время работы ступени ∆ ti – непрерывная переменная в заданном диапазоне, количество параллельно включённых накопителей на ступени n МНЭ – целочисленная переменная.

Ограничения имеют вид:

/ ^ авт >

Х^”         прибл

Zj/^MHD, -7/МНЭ ’ где Pр.допi – допустимое значение выходной мощности накопителя, характеризуемое временем работы i-ой ступени, то естьpМНЭ(/) в соответствии с выражением (4), кВт; Pрi - расчётная мощность i-ой ступени, кВт:

Ppi ⁼ Тнг.ср + ^МНЭ, Ар_{смз С}р + Ипод, Ар_Под.ср ,                           ⁽⁹⁾

где P нг.ср – усреднённая мощность нагрузки по энергии (допущение для упрощения расчётов), кВт; ∆ p _смз.ср – среднее значение мощности, характеризующее часовой саморазряд маховичного накопителя, кВт; ∆ p под.ср – среднее значение потерь мощности, характеризующее поддержание полного заряда маховичного накопителя, кВт; n _МНЭ – количество маховичных накопителей на i -ой ступени, шт; n _под - количество маховичных накопителей, поддерживаемых в полностью заряженном состоянии i -ой ступенью, шт:

^под, = Х',,мнэ,+1 ’                                                    (10)

где n – количество ступеней, шт.

Определим приближённое количество накопителей по выражению (5), шт:

„пРибл =__^У__« 17 92

МНЭ 30-0,58-9    ’ ’ то есть с учётом приблизительной оценки потерь минимальное требуемое количество накопителей равно 18.

Паспортную кривую выходной мощности, используемую в выражении энергии источников (4), в аналитическом виде можно получить с помощью инструмента «Линии тренда» средств MS Excel как полином третьей степени. Выбор типа линии тренда нужно производить для достижения требуемой точности. В графическом виде полученная аналитическая кривая выходной мощности приведена на рис. 1 под номером 2. Наибольшее значение отклонения этой кривой от паспортной составляет 2,7 %, среднее значение отклонения - 1,8 %, что является достаточной точностью приближения.

Выражение для аппроксимированной характеристики 2 выходной мощности имеет вид, кВт:

РмнэИ-^79,73/3 + 857,2/2 -0,589/+ 198,19,

где t – время разряда накопителя, ч.

Поскольку характеристика выходной мощности есть нелинейная функция, то и ограничения для расчётной мощности ступени в системе (8) нелинейны. Поэтому поставленная задача является задачей оптимизации нелинейного программирования [4, 6, 7]. Решение задачи оптимизации удобно выполнить с помощью инструмента «Поиск решения» пакета MS Excel [4, 8, 9, 10].

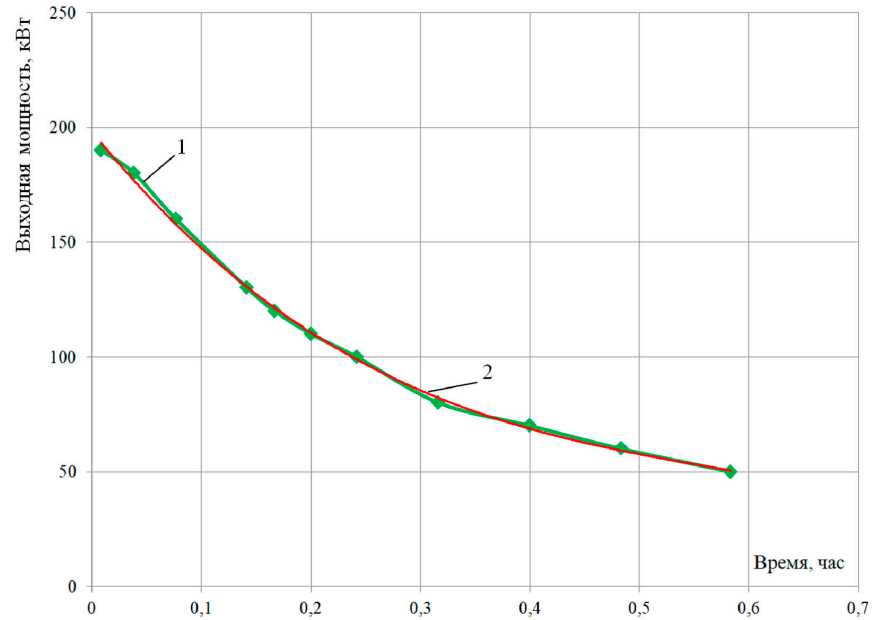
Рис. 1. Выходная мощность накопителя: 1 – паспортная кривая [1], 2 – аппроксимированная зависимость

Fig. 1. FES power output: 1 – passport [1], 2 – regression line

Применяя полученные условия и ограничения, а также связывающие выражения, запишем целевую функцию и создадим форму для решения в MS Excel [4, 10]. Изменяя количество накопителей и время работы каждой ступени, получим оптимальное решение при нулевых начальных условиях. Результаты решения приведены в табл. 1 и 2. Дополнительно введём обозначения расчётной энергии W _р, полной располагаемой энергии накопителей W _р.полн, величины недоиспользованной энергии ∆ W нерац и доли использованной энергии от располагаемой W исп .

Значение КПД в результате решения получилось равным 74,6 %, соответствующее значение целевой функции – 0,746. Учитывая, что каскадная система питания предполагает многократный обмен энергией между маховиками, добиться КПД, близкого к 1, не представляется возможным. Полученный КПД является хорошим показателем. Однако из табл. 3 следует, что недоиспользовано 81,95 кВт∙ч энергии, что составляет почти трёхкратное значение располагаемой ёмкости накопителя.

Выполним автоматизированный расчёт для ненулевых начальных условий, в качестве которых используем результаты первого решения с нулевым приближением. Результаты решения с ненулевыми начальными условиями представлены в табл. 3 и 4. Дальнейшее использование инструмента поиска решения не приводит к изменению результата. Оптимизация распределения количества накопителей по ступеням и времени работы ступеней выполнена, так как КПД вырос до 75,3 %. Однако величина недоиспользованной энергии также выросла до 86,45 кВт∙ч.

Таблица 1. Количество накопителей каскадной системы питания и время работы каждой ступени для времени автономной работы 2 часа при нулевых начальных условиях для 4 ступеней

Table 1. The number of cascade supply system energy storages and the operating time of each stage for an autonomous operation time of 2 hours under zero initial conditions for 4 stages

Ступень	∆ t , час	n МНЭ , шт	n под , шт	P р , кВт	P р.доп , кВт
1 ступень	0,27088	4	14	248,808	367,088
2 ступень	0,58	5	9	242,808	254,161
3 ступень	0,58	5	4	227,808	254,161
4 ступень	0,5691	4	0	206,808	206,808

Таблица 2. Затраченная и располагаемая энергия каскадной системы питания для времени автономной работы 2 часа при нулевых начальных условиях для 4 ступеней

Table 2. Expended and available energy of the cascade power supply system for an autonomous operation time of 2 hours under zero initial conditions for 4 stages

Ступень	W р, кВт∙ч	W р.полн , кВт∙ч	∆ W нерац , кВт‧ч	W исп , о.е.
1 ступень	67,3965	120	52,60	0,562
2 ступень	140,828	150	9,17	0,939
3 ступень	132,128	150	17,87	0,881
4 ступень	117,699	120	2,30	0,981
Суммарное значение	458,052	540	81,95	0,848

Таблица 3. Количество накопителей каскадной системы питания и время работы каждой ступени для времени автономной работы 2 часа при ненулевых начальных условиях для 4 ступеней

Table 3. The number of cascade supply system energy storages and the operating time of each stage for an autonomous operation time of 2 hours under non-zero initial conditions for 4 stages

Ступень	∆ t , час	n МНЭ , шт	n под , шт	P р , кВт	P р.доп , кВт
1 ступень	0,3994	6	12	260,808	412,689
2 ступень	0,4988	4	8	230,808	230,808
3 ступень	0,5327	4	4	218,808	218,808
4 ступень	0,5691	4	0	206,808	206,808

Таблица 4. Затраченная и располагаемая энергия каскадной системы питания для времени автономной работы 2 часа при ненулевых начальных условиях для 4 ступеней

Table 4. Expended and available energy of the cascade power supply system for an autonomous operation time of 2 hours under non-zero initial conditions for 4 stages

Ступень	W р , кВт∙ч	W р.полн , кВт∙ч	∆ W нерац , кВт∙ч	W исп , о.е.
1 ступень	104,156	180	75,84	0,579
2 ступень	115,134	120	4,87	0,959
3 ступень	116,556	120	3,44	0,971
4 ступень	117,699	120	2,30	0,980
Суммарное значение	453,545	540	86,46	0,839

Из полученных двух вариантов выбор оптимального зависит от множества факторов, например, точки зрения специалиста-проектировщика, предпочтений заказчика, простоты и возможности реализации. Выбор первого варианта можно обосновать меньшей величиной недоиспользованной энергии, а второго – большим КПД. Однако представленные варианты по данным характеристикам отличаются незначительно. Предпочтение можно отдать второму варианту, распределение накопителей по ступеням в котором может обеспечить более простую и удобную реализацию.

Увеличим время автономной работы до 4 часов и рассмотрим режим с расчётным запасом энергии 887,72 кВт∙ч и усреднённой мощностью нагрузки 170,7 кВт. В рассматриваемом примере для данного времени работы каскадная система будет крайне невыгодной. В общем случае эффективность каскадной системы снижается при увеличении количества передачи энергии между ступенями системы, что имеет место, когда время разряда на нагрузку применяемых накопителей многократно меньше требуемого времени автономной работы. Исключение составляют случаи, когда максимальная выходная мощность одного накопителя соизмерима с мощностью нагрузки. Поэтому общими факторами снижения эффективности каскадной системы являются многократный обмен энергии между ступенями системы и величина недоиспользованной энергии. Таким образом, целесообразно рассмотреть накопитель, рассчитанный на работу в режиме разряда не менее 4 часов. Подобные накопители отличаются небольшой – 698 – доступной выходной мощностью. Рассмотрим накопитель со временем работы 4 часа, располагаемой ёмкостью 32 кВт/ч и выходной мощностью 8 кВт [2], средней мощностью саморазряда за цикл 100 Вт. Выбор данных накопителей для времени работы меньше 4 часов, в том числе для ранее рассмотренных 2 часов, ограничен величиной недоиспользованной энергии.

Так как время автономной работы не превышает гарантированного времени работы, то выбор числа накопителей будем производить по условию (1), шт.:

р _ 887,72 ''МНЭ “ 32 - 4.0,1

= 28,09,

следовательно, необходимо 29 накопителей по условию баланса энергии; а также по условию баланса мощности (2), шт.:

иР -

Г/МНЭ -

170,7 + 0,1 8

= 21,35,

следовательно, из условия (2) необходимо 22 накопителя.

Принимаем наибольшее из двух значений по условиям (1) и (2), то есть 29 накопителей.

Определим располагаемый объём энергии с учётом потерь на саморазряд, кВт∙ч:

^Ю =”мю(1»^ " Wpac)=29'(3^^

Недоиспользованная энергия накопителей по формуле, кВт∙ч:

^„ерац = ^ - ^р = 916,4 - 887,72 = 28,68.

Доля использованной энергии накопителей, о.е.:

^исп = —^ = ^^ = 0,968.

рграсп 916,4

^МНЭ

Отметим, что данные накопители подключаются к сети постоянного тока. Использование подобных накопителей для времени работы 4 часа при параллельной работе всех накопителей выглядит рациональным решением с точки зрения использования энергии накопителей. Доля использованной энергии составила 0,968 от располагаемой ёмкости накопителей. Величину КПД оценивать в данном случае нецелесообразно, потому что отсутствуют данные о мощности системы собственных нужд накопителя, а также не учитываются потери в инверторе, а имеющиеся данные о величине мощности саморазряда, который составляет в среднем 100 Вт за цикл, приведут к значению КПД, близкому к единице.

Заключение

Полученные условия выбора маховичных накопителей являются необходимыми, но недостаточными. Достаточные условия можно охарактеризовать как условия проверки, количество которых будет зависеть от конкретной системы и выбранного накопителя. Такими условиями могут быть, например, согласование по частоте переменного тока, по напряжению, а в случае некомплектного электромеханического преобразователя необходимо учесть и согласование с мотором-генератором. В то же время полученные условия позволяют рассмотреть работу – 699 –

МНЭ как в параллельной схеме, так и в каскадной; определить как приближённые значения, которые могут быть использованы на этапе рассмотрения выбора накопителей и при недостаточно полных данных о МНЭ, так и более точные значения. Как следует из полученных выражений, их точность зависит от того, насколько полно представлены и учтены исходные данные.

Предложенная методика выбора существующих электромаховичных накопителей энергии может способствовать их стандартизации и распространению на действующих и вновь вводимых объектах.

В рассмотренной методике для параллельной и каскадной систем мощность нагрузки была введена усреднённой величиной по объёму энергии. Такое допущение справедливо, когда величина нагрузки изменяется незначительно. Если изменяющуюся нагрузку нельзя учесть средним значением, то при параллельной работе МНЭ нужно рассматривать условия выбора на каждом интервале, где нагрузку можно считать постоянной. Для каскадной схемы продолжительность работы ступеней должна быть ограничена не только наибольшим рабочим временем разряда, но и продолжительностью работы на одном уровне мощности; величина усреднённой нагрузки в выражении (9) и сама расчётная мощность ступени должны быть рассчитаны с учётом принятых интервалов усреднения мощности нагрузки.