Методика выбора проектных параметров теплового узла термоакустического преобразователя

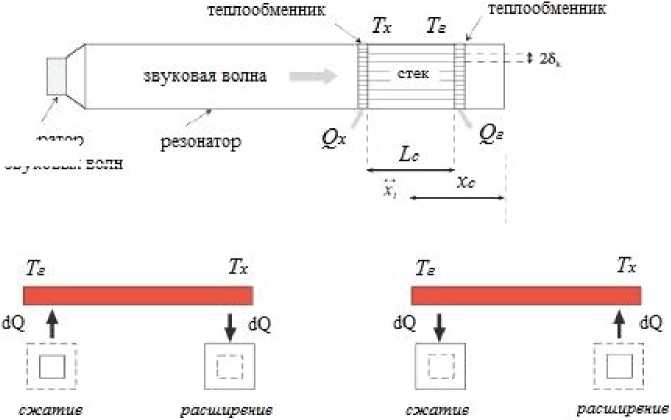
следующем. Так как в регенераторе в направлении перемещения волны сформирован градиент температуры, то при осциллирующем движении газа около некоторого среднего положения (рис. 2) он в крайних своих положениях испытывает попеременное сжатие с нагревом и отдачей тепла и расширение с охлаждением и подводом тепла от поверхности регенератора. Осуществляемый элементарным объемом газа термодинамический цикл, результатом которого является работа деформации, обеспечивает подпитку энергией бегущей волны (для ТАД), либо использование энергии волны для реализации обратного цикла (для ТАХ).

Существующая модель цикла, совершаемого элементарным объемом осциллирующего газа, интерпретирован как цикл Стирлинга. Однако следует отметить, что с таким же результатом можно представить его как цикл Брайтона или Карно, и это не повлияет на результаты сравнения.

Механизм передачи энергии цикла к газу до конца не уточнен, а экспериментально его изучение весьма затруднительно.

Если рассмотреть двигатель (ТАД), то расположенные по обеим сторонам регенератора теплообменники подвода тепла Q_Г и отвода тепла Q_Х , служит для усиления акустической мощности. Благодаря этому входная мощность волны W_Х на холодном конце регенератора возрастает до значения W_Г на горячем конце. Разность между W_Г и W_Х представляет собой акустическую мощность W_А , вырабатываемую регенератором .

Эффективность преобразования тепла в энергию, снимаемую с электрогенератора (как правило, это линейный электрогенератор), можно выразить следующей формулой:

η _e = η _i ⋅ η _тр ⋅ η _эл

W A W M W el Q Г W A W M ^,

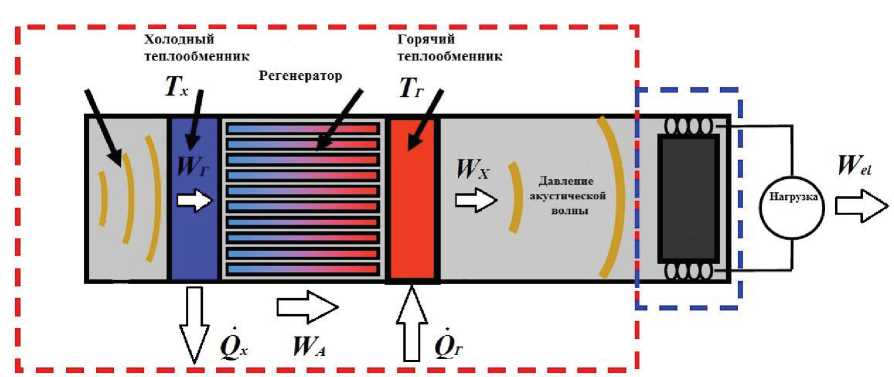
Тепловой узел термоакустического двигателя

Рис. 1. Схема теплообменного узла ТАД

генератор

ЗВУКОВЫХ ВОЛН

Рис. 2. Схема термоакустического преобразователя

где η _e – электроакустическая эффективность преобразователя,

W_A – акустическая мощность,

W _M – диссипативные потери мощности,

W_el – выходная электрическая мощность.

Очевидно, что отношение W_A к подведенному в установку теплу Q_Г будет характеристикой совершенства преобразования тепла в энергию волны.

W η = ^A

Q Г .

В некоторых источниках эта величина обозначается как к.п.д. регенератора. На самом деле этот критерий относится ко всему тепловому узлу преобразователя и является аналогом индикаторного к.п.д. теплового двигателя. Под зтр понимается отношение поглощенной в механической части электрогенератора волновой мощности Wм (с учетом возврата части этой энергии обратно в рабочий контур) к генерируемой акустической мощности WА . Индекс «тр» здесь предлагается интерпретировать еще и как учет всех видов потерь генерируемой волновой энергии во внутреннем контуре ТАП. Электрический к.п.д. генератора зэл относится непосредственно к электрической части преобразователя.

Для холодильной машины (ТАХ) эффективность преобразования тепла можно выразить следующей формулой холодильного коэффициента:

ε _е

= ε _i ⋅ ε _A ⋅ ε _Г

Q Х W A W Г

=------•------•------

.

W A W Г W М

Здесь первый коэффициент еi является внутренним (термоакустическим) холодильным коэффициентом, показывающим отношение количества генерируемого холода к акустической мощности WА, поглощаемой в регенераторе для реализации обратного термодинамического цикла. Второй коэффициент еА - степень преобразо- вания входной (в регенератор) мощности волны Wг в акустическую мощность WА. Третий коэффициент еГ характеризует отношение мощности волны WГ к подводимой извне механической энергии, например, от пульсатора.

Приведенные формулы для эффективности ТАП прямого и обратного циклов могут иметь более подробную структуру.

Современные методики расчета рабочего процесса и определения конструктивных параметров основаны на физико-математических моделях [1, 2].

Целью проектировочного расчета является отыскание таких параметров конструкции, которые отвечали бы необходимой мощности N , получаемой на преобразователе (либо потребной холодопроизводительности Q_Х – для холодильных машин) при заданных температурных уровнях Т_Г и Т_Х газа во внутреннем контуре.

В существующих методиках заложена следующая последовательность действий:

• -    весь рабочий контур ТАП разбивается на основные элементы;

• -    задаются значения температур Т_Г и Т_Х и потребной индикаторной мощности, (либо холодопроизводительности);

• -    задается какая-либо геометрия акустического тракта;

• -    задается уровень давления рабочего тела и само рабочее тело.

Выбирается (или составляется индивидуально) программа расчета, и выполняется расчет каждого выделенного функционального элемента рабочего контура ТАП.

Расчет элемента считается законченным, при условии выполнения граничных условий (по параметрам процесса) с соседним элементом рабочего тракта.

Существующие методики (например, программные продукты Delta E) [3] отработаны и позволяют получить параметры рабочего процесса и характеристики внутреннего контура ТАП. Вполне естественно, что результаты расчета предопределяются допущениями при выборе физической модели и постановкой задачи при математическом описании.

Объективные препятствия по применению результатов расчета накладывают технологические и конструктивные ограничения, обусловленные возможностью изготовления узлов ТАП. Это приводит к тому, что после определения конструктивного облика ТАП изготовленная по результатам расчетов экспериментальная установка требует доработки вплоть до существенных конструктивных изменений, и дальнейших повторений экспериментальных и доводочных работ.

До настоящего времени такая практика проектирования ТАП было обусловлена отсутстви- ем обобщений по тем преобразователям, которые уже работают и имеют приемлемые характеристики, их малочисленностью и закрытостью части работ. Однако за двадцать лет практических наработок (в основном зарубежными фирмами) можно с определенной степенью уверенности использовать теоретический, экспериментальный и практический опыт по ТАП. Это позволит более целенаправленно и обоснованно выбирать конструктивные параметры на этапе проектирования.

Ниже на примере термоакустической холодильной машины предлагаются методические рекомендации, представленные в виде последовательности действий по выбору некоторых основных параметров регенератора на основе оптимизации к.п.д. ТАХ.

Конструктивные параметры холодильника должны обеспечивать заданную мощность охлаждения Q _Х и температурную разницу Δ Т_m . Т а ким образом, для расчета геометрии регенератора (стека) данные параметры будут заданы следующими: Δ Т_m =50 К, Q_Х = 4 Вт. Среднее значение давления в стеке p_m должно быть на сколько возможно большим, поскольку оно определяет акустическую мощность [1]:

⁴         P m c p

При выборе геометрических параметров стека учитывают величину глубины теплового проникновения δ _к , которая пропорциональна корню квадратному из p_m . Слишком высокие значения давления заправки приведут к малым значениям зазора между пластинами, что влечет за собой трудности в изготовлении регенератора. В ранее разработанных термоакустических холодильных устройствах, где в качестве рабочего тела выбран гелий, максимальное значение среднего давления достигало 12 бар. Назначение резонансной частоты f следует производить также учитывая ограничение по геометрическому параметру – глубине теплового проникновения δ _к , которая обратно пропорциональна корню квадратному из частоты колебаний. Высокие значения f также приводят к малому значению зазора между пластинами.

В работе [4] рассмотрены различные виды геометрий стека: с круглыми, квадратными и с профилем равностороннего треугольника порами, а также пластинчатые. Предложены уравнения для теплоты и работы потока в зависимости от функции, зависящей от геометрии поры стека F ( Л ) = 1 — f k , и описываемой в форме, предложенной Свифтом

L =

где f_k – есть функция отношения гидравлического радиуса к глубине термического проникновения δ _к . Кроме того показано, что максимум акустической работы W_А и теплоты Q₂ достигается для случая пластинчатой геометрии стека, а мощность охлаждения, пропорциональна Im( - f_k ) . При оценке максимума Im( - f_k ) при заданных параметрах частоты, среднего давления и гелия в качестве рабочего тела имеем

r_h    y ₀

— — — =1.1, где r_h - гидравлический радиус. ^δ k    ^δ k          ^h

Критический градиент имеет место, когда S T — 2 T 1 — 2 x 1 V T m — 0 , другими словами он определяется разницей температур в двух противоположных точках цикла, когда скорость колебательного движения элементарного объема газа равна нулю и определяется как

T ₁

VTKpum — — , либо с учетом амплитуды ско рости колебаний частиц газа

Так как r h — у 0 , где у₀ - половина зазора между пластинами регенератора, получаем, что зазор между пластинами должен быть не менее 2 y₀ =0.22 мм. Зазор выбирается в диапазоне 2..4 δ к .

В зависимости от способа отвода или подвода тепла и конструктивных особенностей теплового узла по наработанным рекомендациям и экспериментальным данным задается температурный напор между внешним теплоносителем и внутренней поверхностью теплообмена Т _нар - Т _стенки . Оценка КПД цикла Карно в первом приближе-

V7

крит

p 1 ω ^,

О С U1

ρ m p 1

здесь p ₁ – амплитуда изменения давления, ω – угловая скорость (циклическая частота) звуковой волны, c_p – изобарная теплоемкость газа, u ₁ – амплитуда изменения скорости в стеке.

Критический температурный градиент, определяемый разницей температур в двух противоположных точках цикла, которые занимает участок газа, когда его скорость осциллирующего движения равна нулю и записывается как:

нии производится по температурам поверхностей горячего и холодного теплообменников. Предполагая, что температура газа в щелях теплообменников в пределе достигает температуры поверхности, принимаем Т Г ГАЗА — Т_ГСТ , Т Х ГАЗА — Т Х _Ст (в действительности по данным исследования [5] средняя температура газа за время цикла осцилляций отличается от Т_СТ на 2..5?С). Предполагая распределение температуры по длине стека линейным, продольный гра-

^{V Т}крит ^{— Y} S ^Tm^kCt g ⁽ kX c ) ’ ⁽⁹⁾

У 0

где δ _с – половина толщины пластины, х_с – координата положения центра регенератора. Перейдем к безразмерным параметрам:

Δ T / T_m        1         1

h / ( h + 1 ) ( y — 1 ) cot ( kx_C ) kLC '

диент температуры в стеке составит

m

L_С

,

где L_C – длина регенератора (стека).

По принятым в методиках рекомендациям температура поверхности за время осцилляций изменится на величину 2 ⋅ x ₁ ⋅ ∇ T_m , где х ₁ – амплитуда смещения газа при осцилляции. Элементарный объем газа под воздействием акустической волны смещается на расстояние У — 2 x 1 , температура в начале процесса адиабатического сжатия равна T_m - x ₁ ∇ T_m , в конце – T m + x 1 V T m + 2T 1 , изменяясь, таким образом, на 2 T ₁ , где T ₁ – амплитуда изменения температуры, а T_m , p_m – усредненные параметры для элементарного газового объема-частицы.

Безразмерный градиент температуры запи-

где h — 2 у 0 - зазор между пластинами, / - коэффициент адиабаты y — 1.67 для одноатомного газа, t — 2 S _C - толщина пластины, х_с - координата положения центра стека, k – волновое число. Данный параметр Γ содержит независимые величины: заданную температурную разницу, координату положения центра регенератора и длину стека, которые на данном этапе проектирования остаются неизвестными. Вводятся безразмерные группы параметров:

в — УТ. — T1. т

m

т

m

ТГ

^Г – относительный гради-

ент температуры в регенераторе, задается как требование к ТАП, как указывалось ранее Δ Т =50 К и Т =273 К.

m

^ — 2nLc λ

2π⋅ f ⋅Lc c – приведенный пара-

а

шется в виде:

метр длины стека

VT

Г_ m

"vt

крит

.

У с ^{— _}Г" хс ^—     xc - приведенная коорди-

λa

ната положения центра стека.

С учетом [6] задается диапазон изменений 0 <  5 c < 0.78 . Оценка диапазона производилась в связи с тем, что термоакустический эффект здесь наиболее выражен и, следовательно, координата положения центра стека х_с должна находится на 1/8 длины волны от пучности давления.

В результате безразмерный градиент температур запишется как

Г =

9     1

Используя данный комплекс, применим методику приблизительной оценки конструктивных параметров регенератора для термоакустического холодильника в соответствии с работой [6].

Данный ТАХ был сконструирован для режимов с А Т =50К и А Т =25,5К, при среднем значении температуры газа Т_m =273 К. В табл.1 приведены принятые следующие значения безразмерных параметров

Ниже представлены соотношения для безразмерных величин энтальпии ф H (5) и работы потока Ф W (5) как функций только от безразмерных длины стека 5 и координаты положения центра стека 5 с н = - SkhDR2cos(5c )sm(_ )

AP m a        2Y     I I ⁺ ст X^{1 +} e _c X^1- 2 CT¹'² A h + 2стЗ² kh )

1 + ст ¹'² + ст (1 + e_c ) ^с

1 + c r¹'²

^ r ^ ⁹ — ( 1 + ст ( 1 - 25_kh ) ) ,(12)

W = 5» DR ² _x Г       BR ( y - 1 ) cos² ( 5 _C )

AP m a       2 y      [ ( 1 + ст ¹'² )( 1 + _{£ c} )( 1 - 2 ст5 kh ²)

^f BR ⁽ Y ^{- 1 ) cos} 2 5 c ^ Cfit ^{( 9 )} I         -

V      1 + ^£ c

CT ¹'² sin² 5 c        \,

BR ( 1 - 2. a^XT15_kh + 2C8¹ kh ) J'⁵

Далее, используя уравнения (12) и (13) рассчитываем значения энтальпии и работы потока для различных значений безразмерной длины стека 5 . Таким образом, находятся 5 _min = 5 _cr it и 5 ma _x как диапазон выбора оптимальной безразмерной длины регенератора 5 opt (рис. 3).

Критерием определения оптимальной приведенной длины стека является КПДрегенерато-ра, записанный по отношению к КПД цикла Карно. Использование безразмерной записи КПД по Карно удобно тем, что это исключает зависимость данного параметра от температурного напора в регенераторе. КПД в регенераторе по отношению к КПД цикла Карно как функция от безразмерной длины стека 5 запишется как:

Таблица 1. Безразмерные параметры рабочего режима, конструкции регенератора, свойств рабочего тела

Безразмерный параметр	Формула	Зна чени е па раме тра для ра сче та
Зазор между пла ст ина ми регенератора, диапазон значений 0.25 <  6 kh <  0.5 .	51- ^ kh : kh h	0.3
Координата положения центра регенератора	=   2 n f 5 с =      x c a	0.25
Число Пран дтля раб очего тела	ст = ^ E p Л	0.27
Параметр, учитывающий свойства метериала регенератора	/ p m c р Л = 1--------- ^ с V P c c Л с	0.095
Температур ный гра диен т	9 = А Т Т m	0.183
Пори стос ть рег ене рато ра	h BR = h + 1	0.8
Параметр, определяющий отклонение значения пучн ости давления от его средней величи ны	DR = p A pm	0.035

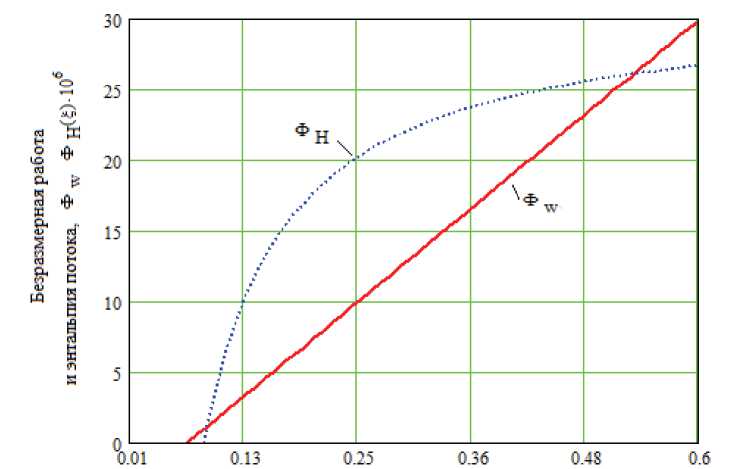
безразмерная длина регенератора. 4

Рис. 3. Предельные значения безразмерной длины стека ξ

_ ^П РЕГ

' КаРно РЕГ „ η КАРНО

(Ф »| -ф W |/ф W I) (2 - 0)/(20)

По графику (рис. 4) для указанных значений приведенных параметров (табл. 1) находим максимум П карноРЕг = 0,42 при безразмерной длине стека § = 0,13 . Оптимизация конструкции на данном этапе производится оценкой η _{КарноРЕГ} при различных значениях координаты центра положения центра стека ξ _с , температурной разницы θ и физических свойствах рабочего тела и материала пластин регенератора.

Зная, что

^П РЕГ =

η КарноРЕГ Γ

здесь Γ – в дополнение к параметру, принятому в (11), характеризует степень соответствия эффективности ТАП и КПД цикла Карно. Параметр Γ подсчитывается по формуле (11), при выбранных значениях безразмерных параметров ξ и ξ _с получаем Г = 0.674. Таким образом, по формуле (14) холодильный коэффициент термоакустического преобразователя е = 0.623

Тогда действительное значение теплоты, подведенной при температуре Т_Х :

Q Х _ Q Х . е = 4 • 0.623 = 2.5 .

Определение площади поверхности регенератора проведем через упрощенные параметры, предложенные в [7], где величина подведенной теплоты Q_Х в безразмерной записи:

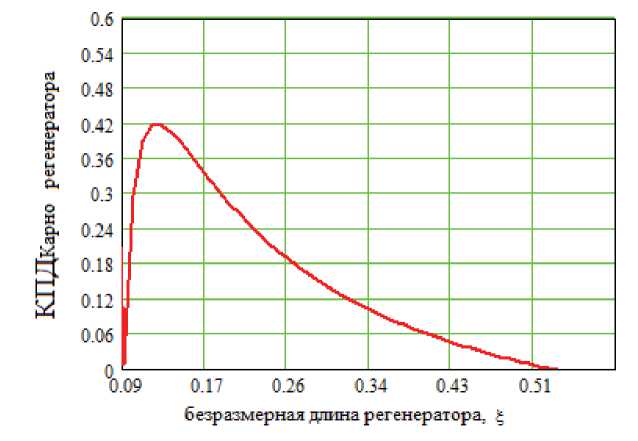
Рис. 4. Зависимость КПД регенератора по циклу Карно в зависимости от безразмерной длины стека ξ

Q

Х прив

Qх - SkhDR 2 • sin(5c) —                            • pm • A • a       8/(1 + с)Л

⁹ • tg ⁵ )   1 + C+ + с

•

( y - 1 ) BR • 5   1 + с

^{( 1} +

с

-

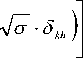
где а – cкорость звука, А – площадь поперечного сечения регенератора. Подставляя значение Q_{Х прив} находим площадь поперечного сечения А = 4.4 см², что дает для цилиндрического регенератора радиус r = 1.2 см.

Таким образом, в результате использования практических рекомендаций, экспериментальных данных и опыта создания термоакустических преобразователей, на этапе проектирования целесообразно применять предложенную в настоящей публикации методику. Она позволяет упростить постановку задачи, более обосновано заложить в проектирование и расчет рабочего процесса начальные исходные данные и сократить трудоемкость проектных работ.