Методика выбора схем транспортирования моногрузов по допускаемым нагрузкам на грузовой пол самолета

При перевозке моногрузов необходимым и достаточным по прочности условием является не превышение погонной распределенной нагрузки на пол самолета (на грузоноситель при колее погрузки 2000<9,6 т/м [3].

Для некоторых моногрузов это условие обеспечивается автоматически из соотношения “длина основания – вес – количество и расположение элементов”. Но для большинства моногрузов выполнение этого условия не очевидно и требует специального анализа.

Теоретической основой для такого анализа может служить теория балок на упругом основании. В этом случае расчетная схема системы “грузовой пол самолета – СПО – груз” имеет вид рис. 1.

В этой схеме роль упругого основания играет пол самолета с уложенным на него грузоносите-лем, а балкой является грузораспределеитель, нагруженный сосредоточенными или распределенными нагрузками. Интенсивность реакции упругого основания определяется формулой:

g(x) = K * V(x) , (1) где К – постоянная, называемая коэффициентом упругого основания, отнесенная ко всей ширине балки и имеющая размерность кг/см².

Связь балки с упругим основанием предполагается двухсторонней, т.е. существует при любом направлении прогиба (вверх или вниз).

Дифференциальное уравнение упругой линии балки постоянного сечения, лежащей на сплошном упругом основании и под действием распределенной нагрузки P(х) имеет вид:

EJ = М(Х) ; EJ = p(x) ; dx2               dx4

EJ V4(x) + K * V(x) = p (x),   (2)

где EJ – изгибная жесткость балки;

Р(х) – непрерывная функция или функция с разрывом первого рода.

Схема сил и перемещений имеет вид:

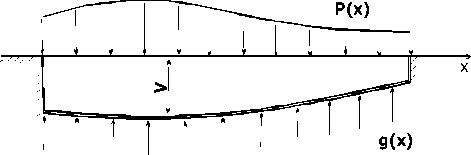
Общее решение уравнений без правой части имеет вид:

V(x) = ePx (A * cosp + B * sin^x) +

+ e" Px(C * cosp + D * sin^x),        (3)

K где P = 4      ;

где 4EJ ;

А, B, C, D – постоянные, определяемые условиями на концах балки

Для дальнейшего анализа особенно важен коэффициент “К”, который определяет распределение перемещений и нагрузок по длине балки.

Входящий в формулу коэффициент упругого основания для системы “грузоноситель – пол самолета” на основании опытных данных следует принимать для ВС Ан-124-100 К=500 кг/см2 как для шпального, так и для бесшпального грузоносителя [2, 3]

Из конкретных случаев нагружения для целей выбора схем транспортирования наиболее важным и часто применяемым является случай нагружения сосредоточенной силой, так к этой схеме приводится большинство реальных схем опирания, в том числе и искусственно, путем установки прокладок, обеспечивающих приложение сосредоточенной силы.

Груз

Опоры груза

Грузораспределитель

Ходовая часть

Грузоноситель(рельс)

Грузовой пол

Рис. 1. Схема системы “грузовой пол самолета–СПО–груз”

Упругое основание

Для случая бесконечно длинной балки, нагруженной сосредоточенной силой, расчетные формулы будут иметь вид:

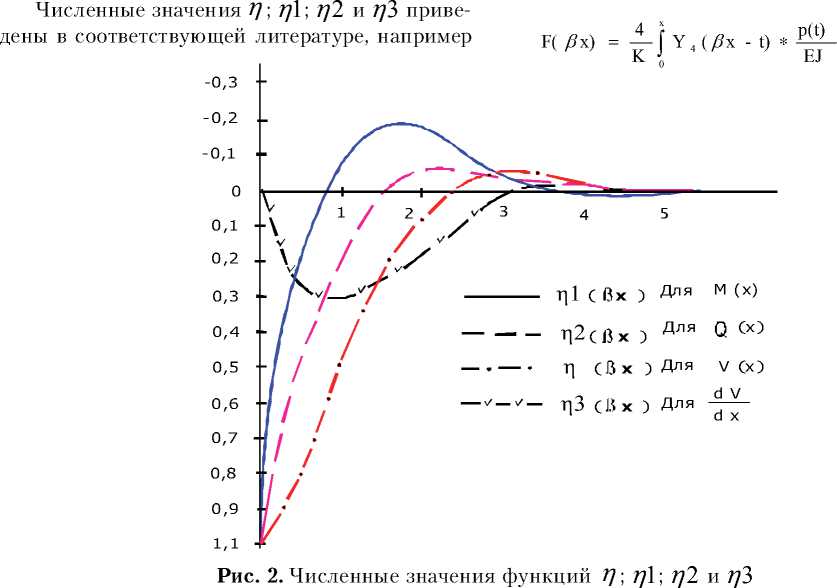
в [1], и для справки показаны на рис. 2.

Приведенные выше формулы и значения входящих в них функций позволяют достаточно про-

EJ^4 = Q(x); 4EJCP1 = -d x3                      2

сто и точно получить распределение нагрузок на

P

и C =--- .

8EJP3

Прогиб

V(x) = ^- e ^P x (sin P x + cos P x) = 8Ej p³

Угол поворота

полу самолета, а также величины силовых фак торов в балке, лежащей на грузоносителе.

В случае действия нескольких сосредоточен ных сил применяется принцип суперпозиции.

-

P

*п 8Ejp3    .

dv dx

-

PP

------ту e ^P sin P x =--- * ^ 3

4EJ P ² 4EJ P ²      .

Изгибающий момент

M(x) = EJ^ = p^P (cos p x-sin p X) = P*^ 1. (7)

Перерезывающая сила

d3v   P A „ P

Q(x) = EJe    = —eP cosPx = — *^2. (8)

dx3    2             2

Предложенная методика расчета не является строгой в математическом смысле, так как не обоснован переход от модели бесконечной балки к балке конечной длины. Однако, в большинстве практических случаев такая замена допустима и существенно упрощает анализ.

Применение данного метода при выборе схем транспортирования реальных моногрузов дало положительные результаты при отсутствии замечаний по прочности, как пола самолета, так и наземного СПО.

В некоторых случаях при проведении более детального анализа при действии нагрузок на балку любой длины, применяется общее решение, данное академиком А.Н. Крыловым [1], согласно которому:

V(x) = A , Y , ( P X) + A 2 Y 2 ( P X) + A 3 Y₃( P ) + A 4^4 ( P x) + F p X) ; (9)

dt

,

где:

Y1 (Px) = cos Px * ch Px ;

Y2(Px) = -^(chPx * sinPx + chPx * cosPx); (10) 2P

Y 3 P ) =

2P

(chPx * sinPx).

Y4( P) =

4p 3 (chPx * sinPx - chPx * cosPx)

обладающие свойством:

dY2       dY3

1                   ;2                   ;               3

dx       dxdx

dY = -4P 3Y4

dx 4.

Слагаемое F( P x) - частное решение уравнения для V(x) при наличии правой части.

Для определение постоянных А1; А2; А3; А4 необходимо удовлетворить условиям на концах балки.

Рассмотрим применение теории, изложенной

ная нагрузка (при n_y=1) составляет 120/10 = 12 тонн/метр , что превышает допустимую величину 9,6 т/м.

Для одной ветви грузоносителя эти величины составляют 6 т/м и 4,8 т/м соответственно. Так как нагрузка от груза передается по четырем сечениям в виде сосредоточенных сил, то превышение допустимых нагрузок на пол будет еще более значительным и для перевозки необходимо применение специальных грузораспределителей.

Как возможный вариант рассмотрим транспортирование на двух тележках, состоящих их двух попарно соединенных балок длиной 6 м. каждая, с расположением относительно ЦТ груза, как показано на рис. 3.

Продольные балки тележек будем рассматривать как балки на упругом основании, принимая К=500 кг/см2 [3]

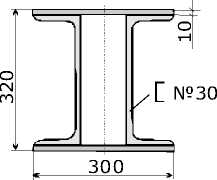
выше к решению задачи о транспортировке моногруза массой 120 тонн, длиной 10 м.

Груз – емкость высокого давления, имеет цилиндрическую форму диаметром D=3 м. и четыре опоры в виде ложементов (рис. 3).

При таких условиях распределенная погон-

Геометрические характеристики балки имеют вид:

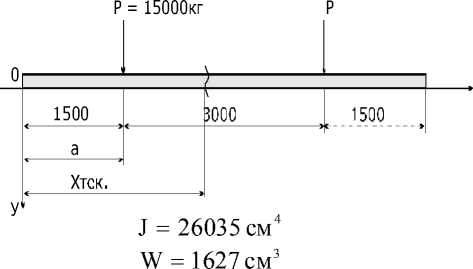
J = 2 * 5 810 + 2 * 1 * 30 * 15.5² = 26035 см⁴

W = 26235

= 1627 см³

ГН

Материал Ст.3, E = 2 * 106 кг/ г см2

Груз

Pi=120=15т

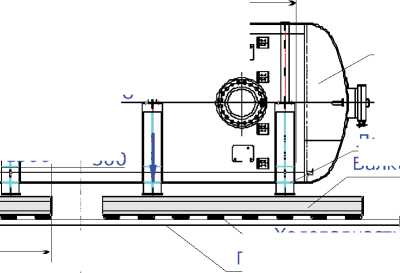
Ходоваячасть Грузоноситель

Ложемент

Балка

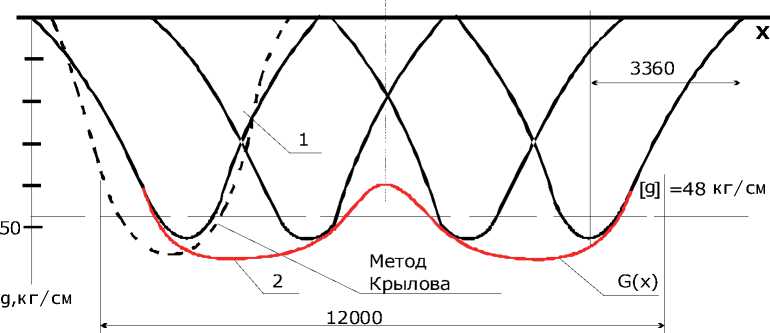
Рис. 3. Схема транспортировки и распределения нагрузок

Тогда

К 500

---- = 4 ------------------

4EJ V 4 * 2 * 10 * 26035

= 0,007 . (11)

По рис. 2. находим, что 7 ? ( P x) = 0 при n x =2,35

2,35

х =----= 336 см

Тогда 0,007 и

V max

P * P = 15000 * 0,007 2K " 2 * 500

= 0,105 см (12)

g max = K * V = 500 * 0,105 = 52,5 кг/см (13)

Распределение нагрузки по упругому основанию от сосредоточенной силы имеет вид – кривая “1” на рис. 3. Применяя принцип суперпозиции, найдем результирующую кривую распределения нагрузки по упругому основанию от системы 4ех сосредоточенных сил – кривая “2” на рис. 3.

Как видно с графика, на длине ~12 м. нагрузка распределяется практически равномерно и незначительно превышает допустимую величину ([g] = 48 ^кг/с_м ). Следовательно, выбранная схема транспортирования обеспечивает допустимое распределение нагрузок, легко реализуема и не выходит за габариты грузовой кабины самолета.

Как показывает многолетний опыт выполненных перевозок моногрузов, допускаемая неравномерность нагружения по длине может составлять до 20%, т.е. g(x) может лежать в диапазоне g(x) =48±10 кг/см.

Для сравнения рассмотрим задачу о распределении нагрузок для той же схемы транспортировки моногруза с помощью метода академика А.Н. Крылова [1]. Расчетная схема для одной балки тележки имеет вид:

K = 500 ^кг/ .

см2

L = 600 см безразмерная (или относительная) длина балки: Р* L = 0,007 * 600 = 4,2

относительная абсцисса места приложения силы Р: Р * a = 0,007 *150 = 1,05

Упругая линия балки в методу Крылова выражается уравнением:

V(x) = [A , Y , ( P x) + A 2 Y 2 ( P x) +

+ A 3 Y 3 ( P x) + A₄Y₄( P x)] + -K Y 4 ( P x-1)];

4EJ

При наличии свободного опирания на левом конце балки (х=0) А3=0 и А4=0. Краевые условия на правом конце: Q(x)=0 и М(х)=0 приводят к следующим уравнениям относительно неизвестных постоянных А1 и А2

„„ mP

A_lY 3 ( P x) + A_!Y 4 ( P <)---Y_J( P _t) = 0 ;

K

„„ mP

A 1 Y 2 ( P x) + A 2 Y 3 ( P x)-—^Y 1 ( P x) = 0 .

K

По таблицам Крылова [1] находим

Y 3 (4,2) = - 14,527 ; Y 4 (4,2) = - 3,2 ;

Y 2 (4,2) = - 22,7 ; Y 2 (3,15) = - 5,87 ; (16)

Y 1 (3,15) = - 11,69

Подставляя численные значения Yi в систему (15), получим:

• - 14,527* А 1 - 3,2* А ₂ + 1,23 = 0 ;

• - 22,7* А 1 + 14,527* А₂ + 2,45 = 0 . ⁽ 7)

Решая систему (17), получим: А1=0,072;

А2=0,055

V(x) = A1Y1(px) + A2Y2(Px) =

= 0,072 * 0,798 + 0,055 * 1,008 = 0,113 см

g(x) = V(x) *K = 0,113*500 = 56,4 ^KV см

На левом конце балки (х=0) имеем:

V(0) = A1Y1(0) + A2Y2(0) =

= 0,072 * 1 + 0,055 *0 = 0,072 см

g(0) = V(0) * K = 0,072 * 500 = 36,0 KV см

Определим, на какой длине от точки приложения силы Р V(x) = 0:

A , Y , ( P x) + A 2 Y 2 ( P x) = 0

или A₁Y₁( P x) = - А ₂Y₂( P x) .

0,072

Y 2 ^{( P x)} = ^- 0 055 ” -^Y .     (22)

,

По таблицам фундаментальных функций Крылова находим, что это условие выполняется при a =1,84.

Так как P = a * Х „ , то тек ^, , „ 1 84

Х = aP = -^8— = 263 см

• ^V = ⁰           0.007            .

Результаты расчета показаны на рис. 3. пунктиром для одной силы.

Анализ результатов расчета показывает, что сходимость обоих методов вполне приемлема для практических целей при существенно большей трудоемкости метода Крылова, который целесообразно применять для наиболее ответственных перевозок.

Для оперативной оценки характера распределения нагрузок в зависимости от жесткости грузовой балки или платформы на рис. 4 дана зависимость величины Х от момента инерции балки и нанесено значение Х для рассмотренной задачи (при J=26035 см4)

Кроме Анализа распределения нагрузок на основании, необходимо проверять и прочность самой балки, хотя, как показывает опыт, условие прочности в большинстве случаев выполняется автоматически.

Так, например, для рассмотренной задачи имеем:

M_ma = — = ¹⁵⁰⁰⁰ = 535714 кг * см . (23) max 4 р 4*0,007

С учетом перегрузки ( n y = 4 )

M = 535714 *4 = 2142856 кг * см ; (24) max

^ = M mx = 2142856 = 1317 <  [ ^ ] = ²⁴⁰⁰^2- .(2 5) W 1627                  см ²

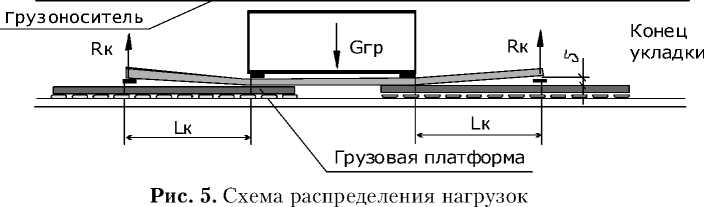
Следует отметить, что при выборе схем транспортирования моногрузов требуется определенная изобретательность и анализ опыта уже ранее выполненных перевозок УНГ. Так, например, для грузов малой длины требуется грузораспре-делитель большой длины и жесткости, а, следовательно, и строительной высоты, что не всегда возможно для высоких грузов. В этом случае целесообразно применение прокладок, которые позволяют часть нагрузки гарантированно разнести на концы грузораспределителя по схеме, представленной на рис. 5.

Величина R _k зависит от жесткости балки грузораспределителя, высоты прокладки § и длины консоли L_k. Как правило, следует добиваться, чтобы R_k составляла 8-12 тонн, что как бы “облегчает” мало протяженный груз на 3248 тонн и позволяет оставшуюся нагрузку распределить на сравнительно малой длине. При этом надо обязательно проверять прочность консольно-деформируемой части балки грузо-распределителя.

Любая уникальная грузовая авиаперевозка означает:

• •    исследования технических особенностей груза (работа с Заказчиком);

• •    специальное техническое решение на конкретную перевозку, выполняемое профессионалами, объединяющими экспертизу, технологию и новые идеи;

• •    проектирование и изготовление дополнительного специального погрузочного оборудования (при необходимости);

• •    инженерное сопровождение каждой конкретной уникальной перевозки.

Транспортный оператор должен обладать эксклюзивным опытом по уникальным авиаперевозкам крупногабаритных грузов; наличию квалифицированного персонала и сети технических баз и офисов по всему миру; иметь высокие технологии погрузочно-разгрузочных работ по крупногабаритным (нестандартным) и тяжеловесным грузам.

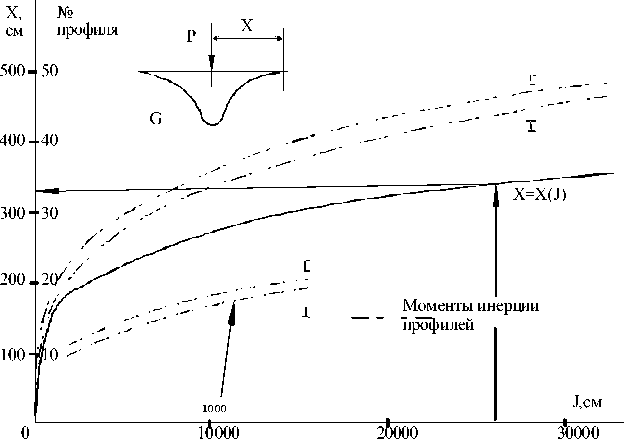
Рис. 4. Распределение давления g от силы Р по балке на упругом основании

Начало укладки

Грузораспределитель

Прокладка