Методологический подход к решению проблемы обоснования требований к системе инженерно-аэродромного обеспечения боевых действий авиации ВВС

К настоящему времени в ВВС возникла проблемная ситуация в практической области. С одной стороны, боевые возможности средств воздушного нападения потенциального противника непрерывно возрастают, что позволяет в динамике боевых действий усложнить обстановку до такой степени, что решение задач инженерно-аэродромного обеспечения (ИАэО) боевых действий авиации на постоянных аэродромах ВВС становится подчас невозможным.

С другой стороны, крайне низкая защищенность базирования авиации (не более 12 %) и объектов аэродромной сети, отсутствие нормативной базы в отношении требований, обеспечивающих проектирование и строительство современных защитных укрытий на аэродромах, непрерывное снижение возможностей инженерно-аэродромных частей и подразделений, способных выполнить только около 20 % требуемого объема инженерно-технических работ по маскировке войск и имитации объектов на аэродромах, сокращение инженерно-маскировочных частей в ВВС. Кроме того, отсутствие на сегодняшний день единых нормативных требований к

В этих условиях возникает проблема прагматического характера, заключающаяся в необходимости приведения характеристик системы инженерно-аэродромного обеспечения боевых действий авиации ВВС к прогнозируемым потребностям при подготовке и ведении боевых действий с учетом развития средств воздушного нападения противника и авиации ВВС РФ. Одним из возможных направлений разрешения этой проблемы является создание системы инженерно-аэродромного обеспечения боевых действий авиации ВВС на основе научно обоснованных требований к значениям ее характеристик.

Инженерно-аэродромные мероприятия по маскировке аэродромов, обеспечению живучести базирования авиации и скоростному восстановлению постоянных аэродромов государственной авиации включают: строительство зон рассредоточения; совершенствование фортификационной защиты авиационной техники; рассредоточение авиационной техники и аэродромных сооружений; разукрупнение и дублирование элементов аэродрома; увеличение прочности несущих и ограждающих конструкций сооружений; проведение инженерномаскировочных мероприятий и мероприятий по созданию ложных позиций, внедрение в практику скоростного восстановления аэродромов перспективных способов, основанных на применении быстротвердеющих РВМ и требующих комплексного применения и соответствующего оперативно-тактического и военно-экономического обоснования. Поэтому обоснование требований к характеристикам системы ИАэО боевых действий авиации на постоянных аэродромах ВВС целесообразно осуществлять с учетом результативности инженерно-аэродромных мероприятий и их стоимости.

Проведенный анализ состояния методологии обоснования требований к системе ИАэО боевых действий авиации указывает на отсутствие к настоящему времени единого методологического аппарата, позволяющего с точки зрения системного подхода разрешить объективно существующие противоречия и учесть все многообразие взаимодействующих и воздействующих на систему ИАэО значимых факторов. Это обстоятельство порождает противоречие в научном плане между объективной необходимостью разработки нового научно-методологического аппарата и отсутствием единой методологии обоснования требований к системе ИАэО боевых действий авиации с системных позиций.

Наличие прагматической проблемы, порожденной противоречиями в практике, и противоречия в научном плане порождают научную проблему, состоящую в разработке методологии обоснования требований к системе инженерно-аэродромного обеспечения, позволяющей обеспечить требуемый уровень потенциальных боевых возможностей авиации ВВС в ходе боевых действий при минимизации суммарных экономических затрат, связанных с созданием и функционированием этой системы за время, не превышающее располагаемое.

Разработка методологии обоснования требований к системе инженерно-аэродромного обеспечения боевых действий авиации (ИАэО) на постоянных аэродромах ВВС состоит в разработке методов и их последовательном применении для обоснования требований к системе ИАэО, которая должна обеспечить необходимую эффективность боевых действий авиации. Для этого нужно соответствовать необходимым требованиям некоторого векторного показателя качества F = (F₁, F₂,..., F_i,..., F_m) , где F _i (i ∈ 1, m) – частные показатели качества.

Значения каждого частного показателя F _i (i ∈ 1, m) определяются некоторыми факторами (x₁,...,x_j,...,x_n), описывающими параметры объекта исследований – системы инженерноаэродромного обеспечения боевых действий авиации на постоянных аэродромах ВВС, параметры предмета исследований – взаимосвязь и взаимовлияние параметров системы инженерно-аэродромного обеспечения боевых действий авиации ВВС, а также параметры внешней по отношению к ним среды, т. е. F_i (x₁,...,x _j,...,x_n). Значения факторов выбираются с учетом реально существующих ограничений, в этом смысле существует Ω _X – область допустимых значений факторов x = (x₁,...,x_j,...,x_n)^T из n–мерного векторного пространства Е_n ( Ω _X ⊆ E_n) . Каждый фактор x _j в области допустимых значений имеет минимальное x _jmin и максимальное x jmax значения и в общем случае может иметь дискретные или непрерывные значения. Для наглядности на рис. 1 показано формирование области допустимых значений для трех факторов в трехмерном пространстве.

Каждая точка факторного пространства x = (x₁,x₂,x₃) имеет вполне определенное значение каждого фактора. Так, на рис. 1 значение первого фактора равно – x₁ , второго – x₂, третьего – x₃ .

Принцип формирования допустимых значений для любого n числа факторов в n – мерном факторном пространстве остается таким же.

При изменении вектора факторов x в области Ω X вектор частных показателей качества F_i (x) = F_i(x₁,...,x_j,...,x_n) будет изменяться в некоторой области Ω_F m–мерного пространства

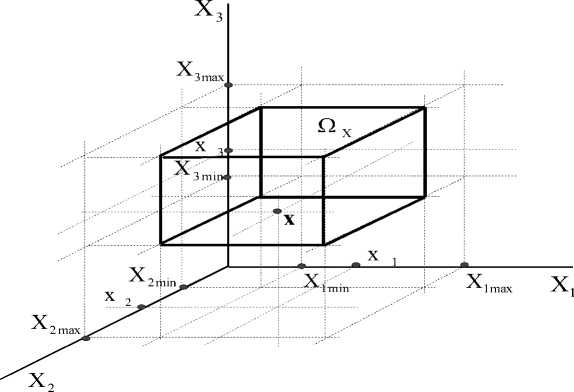
Рис. 1. Формирование области допустимых значений для n = 3 факторов в трехмерном пространстве E 3^(fix - ^Ез)

Е_m ( Ω _F ⊆ E_m) векторного показателя качества F, являющегося отображением области Ω_X допустимых значений факторов x = (x₁,...,x_j,...,x_n)^T в пространстве Е_m ( Ω _F ⊆ E_m) частных показателей качества F_i (x) = F_i (x₁,...,x_j,...,x_n) .

Область Ω F представляет собой область Парето, или область возможных значений частных показателей качества F_i (i ∈ 1, m) . На рис. 2 для наглядности показано формирование области Ω F для трехмерного векторного показателя качества, т. е. когда i ∈ 1, m при m = 3.

На рис. 2 векторная оценка F* = (F₁^* ,F₂^* ,F₃^* ) , являясь элементом множества Ω_F векторных оценок, соответствует возможным в данных условиях показателям F i (x), ∀ i ∈ 1,3 , рассчитанным для одних и тех же значений факторов из области x ∈ Ω_X. Принцип формирования области Ω F для любого числа m векторных показателей качества в m–мерном пространстве остается таким же.

Задача оптимизации со сравнением альтернативных решений x ∈ Ω X по предпочтительности при помощи заданных на Ω_F скалярных показателей в виде функций F_i(x) для ∀ i ∈ 1,m приводит к задаче векторной оптимизации [1, 2].

Задачи векторной оптимизации можно свести либо к задаче векторной максимизации (когда все показатели качества F i (x), необходимо увеличивать), либо к задаче векторной минимизации (когда все показатели качества F_i(x) необходимо уменьшать). На практике чистые задачи векторной максимизации (минимизации) встречаются редко, при этом часть векторных показателей качества необходимо увеличивать, а часть уменьшать. В этом случае пользуются искусственным приемом, который заключается в том, что в задаче векторной максимизации (минимизации) тот векторный показатель качества F_i(x), который надо уменьшить (увеличить), заменяют показателем [–F i (x)], и его уже надо увеличивать (уменьшать) [13].

Наиболее представительным является векторный показатель качества вида F = (F 1 ,F 2 ,F 3 ) , где F₁ = С(x₁,...,x_j,...,x_n) - частный показатель, характеризующий стоимость создания и функционирования системы ИАэО боевых действий авиации; F₂ = Э(x₁,...,x_j,...,x_n) - частный показатель степени выполнения системой ИАэО своего функционального назначения, характеризующий полезный целевой эффект от ее применения; F₃ = Т(x₁,...,x_j,...,x_n) - частный

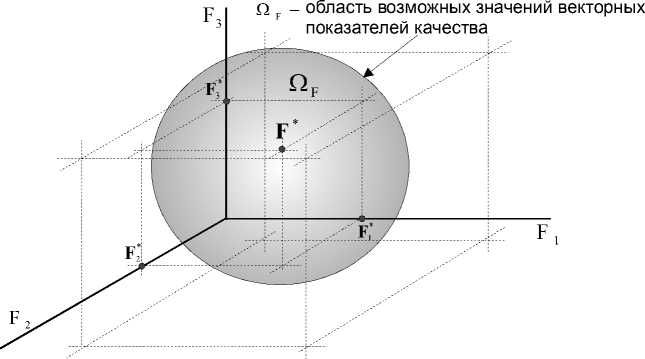
Рис. 2. Формирование области Q F трехмерного пространства E 3 (Q F С E 3 ) для F i , i е 1,3

показатель, отражающий временные характеристики функционирования системы инженерноаэродромного обеспечения боевых действий авиации при достижении полезного целевого эффекта.

К настоящему времени эффективных методов решения задач векторной оптимизации не разработано. Приемлемый метод при их решении может состоять в выборе компромисса. Одной из часто применяемых схем компромисса является определение главного показателя, заключающееся в том, что из векторного показателя выделяется один показатель, называемый главным, а на остальные частные показатели накладываются ограничения.

В решаемой научной проблеме в качестве главного показателя целесообразно выбрать частный показатель F 1 = C(x₁,...,x_j,...,x_n), характеризующий стоимость создания и функционирования системы ИАэО боевых действий авиации, поскольку априорно нельзя, даже приблизительно, определить диапазон изменения его значений. Показатели F 2 = Э(x₁ x j x_n) и F 3 = T(x 1 x j x_n) могут выступить в качестве показателей, на которые накладываются критерии пригодности. При этом показатель F 2 = 3(x₁,...,x_j.,...,x_n), характеризующий полезный целевой эффект и отражающий степень выполнения системой ИАэО всего объема задач, имеет диапазон изменения от 0 до 1. Значения показателя F₃ = T(x₁,...,x_j,...,x_n), характеризующего временные характеристики функционирования системы ИАэО при достижении полезного целевого эффекта, могут быть заданы исходя из рассмотрения процессов ее функционирования во временной области.

Важным при разработке и постановке проблемы обоснования требований к системе ИАэО боевых действий авиации является выбор из области Q_X допустимых значений факторов x = (x 1 x j x_n) ^T в n-мерном векторном пространстве E_n(Q X с E_n) совокупности факторов (аргументов), значения которых оптимизируются в совокупности факторов, только учитываемых в рамках поставленной научной проблемы. Для этого разобьем область Q_X допустимых значений факторов x = (x 1 x j x_n) ^T на три непересекающиеся области так, что

QX = QX U «X U Пх, = U«X .(1)

i=1

В выражении (1): Q _X - область допустимых значений оптимизируемых факторов (аргументов)

X = (x1,...,xl)T е x = (x1,...,xj,...,xn)T,(2)

характеризующих параметры системы инженерно-аэродромного обеспечения боевых действий авиации на постоянных аэродромах ВВС;

«X1 - область допустимых значений k учитываемых факторов

X2 = (xl+1 xi+k)T е x = (xi xj xn)T ,(3)

характеризующих параметры средств нападения противника, форм и способов их применения по аэродромам базирования группировки авиации объединения ВВС;

« _X - область допустимых (r = n -1 + k) значений учитываемых факторов

X3 = (xl+k+1 xn)T е x = (xi xj xn)T ,(4)

характеризующих параметры своих войск.

В выражениях (2 – 4) n–мерный вектор всех факторов разбивается на l-мерный вектор факторов, характеризующих параметры системы инженерно-аэродромного обеспечения боевых действий авиации, k-мерный вектор факторов, характеризующих параметры средств нападения противника, форм и способов их применения по аэродромам базирования авиации и r-мерный вектор факторов, характеризующих параметры своих войск так, что l + k + r = n.

В свою очередь, вектор X 1 = (x 1 ,...,x l )^T преобразуется к виду

X 1 = ( G 1 , G 2 , G 3 , G 4 , G 5 , G 6 ) X 1 ^eQ _х,                                                   (5)

По существу, элементы вектора X] представляют собой значения возможных характеристик, а обоснование требований к системе ИАэО боевых действий авиации ВВС – это выбор из значений всех возможных характеристик в области Q _X таких значений X * , которые, удовлетворяя требованиям по эффективности и времени функционирования в областях Q _х и Q _х , обладали бы минимальной стоимостью.

Формализованная математическая постановка сформулированной научной проблемы может быть представлена следующим образом.

Необходимо минимизировать целевую функцию на множестве значений оптимизируемых факторов (аргументов) X ₁ ( G ₁ , G ₂ , G ₃ , G ₄ , G ₅ , G ₆ ) е п _х , принадлежащих области Q _х их допустимых значений:

С _х ( X 1 / X ₂ , X ₃ ) ^ min                                                  (6)

Xl'\, при ограничениях:

Э ИАэО ( X 1 / X 2 , X 3 )≥Э ИАэО(тр) ,

Т( X 1 / X 2 , X 3 ) ≤ Т расп

X 1⁽ G 1 , G 2 , G 3 , G 4 , G 5 , G 6 ) ^Q „                                                7

X 2 ∈ Ω X 2 ,

X3 eQХз , где СΣ(X1 /X2,X3) – суммарные затраты на создание и функционирование системы ИАэО боевых Σ123

действий авиации;

Э _ИАэО ( Х 1 / Х ₂ , Х ₃ ),Э _{ИАэО(тр} — значения текущей и требуемой эффективности функционирования системы ИАэО боевых действий авиации;

Т( X ₁ / X ₂ , X ₃ ), Т _расп – значения времени и располагаемого времени функционирования системы ИАэО боевых действий авиации;

X 1 ( G 1 , G 2 , G 3 , G 4 , G 5 , G 6 ) – вектор факторов, характеризующих варьируемые параметры системы инженерно-аэродромного обеспечения боевых действий авиации на постоянных аэродромах ВВС;

Х ₂ - вектор факторов, характеризующих параметры средств нападения противника, форм и способов их применения по аэродромам базирования группировки авиации объединения ВВС;

Х ₃ - вектор факторов, характеризующих параметры своих войск.

Ω _X1 , Ω _X2 , Ω _X3 – области допустимых значений факторов.

Решение оптимизационной задачи вида (6, 7) направлено на сужение области Парето П „ определяющей допустимые варианты построения системы ИАэО боевых действий авиации до области эффективных (Парето-оптимальных) решений Ω ⁽ F ^ЭФ) . Для отыскания области Парето-оптимальных решений П Г) в задаче вида (6, 7) формируется множество ограничений, включающих значения требуемой эффективности и располагаемого времени функционирования системы ИАэО. Формирование множества ограничений осуществляется следующим образом. Весь диапазон изменения значений требуемой эффективности разбивается на i ∈ 1,I участков, каждому из которых приписывается значение требуемой эффективности Э (Тр , а диапазон значений располагаемого времени на j ∈ 1, J участков, каждому из которых приписыва е тся значение располагаемого времени Т РаС, .

В результате имеем векторную матрицу ограничений вида

	о 11      .	.. о1j .	.. о1J
О ij =	...        . о i1      .	..        ...        . .. о . ij	..         .. . ..      о iJ
	...        . о I1      .	..        ...        . 0 r ..             Ij         .	..        ... ..     о IJ

Каждый элемент матрицы (8) представляет собой вектор о ij = (Э Т) , T_p JC _n) .

Область Парето-оптимальных решений отыскиваются путем многократного, i × j раз, решения задачи минимизации целевой функции (6) на множестве значений аргументов X ₁ ( G₁ , G 2 , G 3 , G 4 , G 5 , G₆ ) eQ _X , и множестве ограничений o j , i e 1,I, j e 1,J. '

Все решения оптимизационной задачи можно свести к виду, изображенному на рис. 3 в трехмерном пространстве.

На рис. 3 треугольниками показаны решения оптимизационной задачи (6, 7) в системе координат (Э_тр, 0, С) при значениях располагаемого времени T _р ⁽ _а ^J _с ⁾ _п , квадратиками – в системе

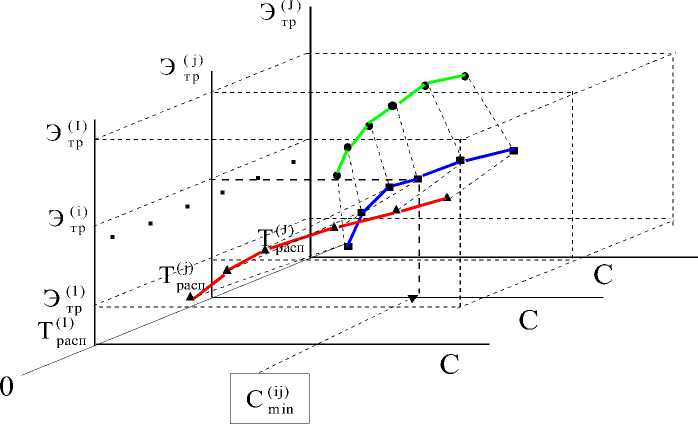
Рис. 3. Область оптимальных (по Парето) решений

координат (Э_тр, 0, С) при значениях располагаемого времени T _pJ , кружочками - в системе координат (Э тр , 0, С) при значениях располагаемого времени T _р ⁽ _а ^J _с ⁾ _п . Каждая точка в трехмерном пространственарис.3принадлежитобласти П ^^Ф) е П _F,носодержиттолькотеэлементы,которые для зафиксированных значений факторов в составе векторов X 2 е Q X , X 3 е Q X , имея векторную оценку F ⁽ⁱ⁾, удовлетворяют условию F ⁽ⁱ⁾ = (C ⁽m^i,i^jn⁾ (X 1 /X 2 ,X 3 ), Э(X 1 /X 2 ,X 3 ) ≥ Э ⁽трⁱ⁾ , Т(X 1 /X 2 ,X 3 ) ≤ Т ⁽р^jа⁾сп ) , при этом значения составляющих вектора X ₁( G₁ , G 2 , G₃ , G 4 , G 5 , G 6 ) оптимальны в рамках принятых ограничений.

Решая задачу (6, 7) для интересующих значений факторов в составе векторов Х ₂ efi X ₃ eQ _X , можно получить совокупность Парето-оптимальных поверхностей, по которым лицо, принимающее решение, может выбрать удовлетворяющее его решение по характеристикам системы ИАэО боевых действий авиации. По своей сути задача (6, 7) представляет собой задачу структурно-параметрического синтеза системы инженерно-аэродромного обеспечения боевых действий авиации на постоянных аэродромах ВВС при известных исходных данных, характеризующих противника X ₂ е о X и свои войска X ₃ е о X . При этом отыскиваются оптимальные, в рамках принятых ограничений, наборы значений характеристик подсистемы маскировки аэродромов ( G 1 , G₂ ) , подсистемы обеспечения живучести базирования авиации ( G₃ , G 4 ) и характеристик подсистемы скоростного восстановления аэродромов в ходе боевых действий ( G 5 , G 6 ) , составляющих основу функционирования системы инженерно-аэродромного обеспечения боевых действий авиации на постоянных аэродромах ВВС.

Таким образом, проведенное описание функционирования системы ИАэО с детальной формализованной постановкой научной проблемы позволит перейти к формированию логической организации общего системного подхода по обоснованию требований к системе ИАэО боевых действий авиации на постоянных аэродромах ВВС, которая предполагает следующие процедуры: выбор исходных данных по противнику и своим войскам; обоснование и выбор характеристик и показателя эффективности функционирования системы ИАэО; выбор характеристик системы ИАэО, подлежащих оптимизации; моделирование процессов функционирования системы ИАэО и расчет значений показателя ее эффективности; решение оптимизационной задачи для выбранных вариантов вооруженного противоборства и выбранных ограничений с формированием областей Парето-оптимальных решений для различных исходных данных; выбор рационального варианта построения системы ИАэО боевых действий авиации в различных условиях боевой обстановки.