Методология анализа малых рек и маломасштабных водных объектов при их многочисленности для планирования водохозяйственной деятельности

нагрузку и др. Существенны хозяйственноэкономические, экологические, демографические соображения. К структурным компонентам МР следует отнести и другие малые водные объекты: пруды и запруды, ручьи, рассматриваемые как притоки и истоки МР, малые болота. Все указанные объекты объединяются общим понятием маломасштабных водных объектов (МВО), предложенным в [15].

Основная идея анализа МВО состоит в том, чтобы в пределах региона разбить всё их множество на классы , где класс понимается как совокупность некоторого числа водных объектов, похожих друг на друга по определенным признакам. Тогда можно изучать не каждую отдельную реку, а образуемые классы в целом путем выбора в них представительного водного объекта, - типового объекта, - распространив результаты его изучения на все остальные объекты класса. Для возможности такого подхода необходимо, чтобы классы выделялись на множестве всех МВО однозначно, чтобы каждый малый водный объект попадал при их классификации лишь в один класс.

При описании природных объектов, к каким относятся малые реки и другие водные объекты, невозможно оставаться в рамках соответствий «четких множеств». Оценки, по которым водные объекты могут сравниваться, оценки экологического состояния, хозяйственного значения, качества воды и пр. могут быть разработаны на основе теории нечётких множеств [6]. Но в настоящей работе это не обсуждается, а формализация получения классов МР и МВО опирается на доказательства без использования указанной теории. Каждому классу присущи определенные системные свойства в рамках научных дисциплин (экономика, экология, гидравлика, распространение загрязнений и др.) и научно-практической деятельности (проектирование сооружений, охрана объекта, защита от вредного воздействия вод и пр.). Разбиение всего множества МВО на классы и выбор в каждом классе типового водного объекта преследует цель значительно сократить число малых рек и других водных объектов, подлежащих детальному изучению индивидуально, таким образом, чтобы можно было бы реально выполнить всю эту работу, и, распространив результаты изучения типовых МВО каждого класса на все водные объекты классов, получить качественно и количественное представление в каждом классе МВО об их поведении, особенностях, составе и объемах работ по охране, защите, поддержанию МВО в надлежащем состоянии.

Между понятиями классификации и типизации существуют различия. Классификация состоит в систематизации объектов, распределении по классам на основании определенных признаков, рассматривая каждый объект в целом. Типизация подразумевает рассмотрение частей -элементов объектов, выделяя типовые элементы, и конструирование из них целого объекта уже как типового. Например, если признаком малых рек является ландшафт местности, где они текут, то классификация будет заключаться в разделении на равнинные, горные реки и пр. При типизации выделяются элементы морфологии - русло, меандры, террасы. Выбрав основную форму русла, средних размеров меандр, среднюю ширину террасы, сконструированная из этих элементов река будет типовой . Однако действия по выделению элементов и конструированию из них типовых объектов на множестве природных МВО чрезвычайно трудоемки и плохо поддаются автоматизации. Поэтому в качестве «типового» в каждом классе МВО выбирается некий средний объект по признаку максимального сходства его с другими объектами класса.

Сходство водных объектов далее формализовано на основе понятия близости их друг к другу. В каждом классе МВО выбирается реально существующий водный объект, наиболее схожий со всеми другими объектами, и объявляется как типовой. Выбор этого объекта может сопровождаться экспертными соображениями и эвристическими приемами. Исследование классов МВО ведется на примере выбранного типового представителя каждого класса и состоит в применении методов разных научных дисциплин: гидравлика установившегося, не-установившееся движения воды, гидрология (фазы и особенности формирования стока, зимние явления и пр.), распространение загрязнений, движение наносов, формирование русла (переработка берегов, устойчивость откосов). Указанные исследовательские модели применимы на первом шаге изучения типового водного объекта.

Следующим шагом является планирование на типовом водном объекте мероприятий по улучшению состояния объекта, его обустройству и охране. Речь идет об установке сооружений (мостов и переходов) на реке, укреплении берегов, обваловании, если необходимо, и пр. Как правило, к малой реке привязываются типовые сооружения. Используются математические модели решения комплексных задач с оптимизацией водохозяйственных мероприятий: выбор расположения плотин, расстановки очистных сооружений, линий валов, определение параметров сбросных сооружений, насосных станций, дамб и пр. В каждом классе оцениваются финансовые, материальные, трудовые ресурсы на проведение нужных водных и водохозяйственных мероприятий как по всей совокупности водных объектов в классе и по каждому объекту класса в отдельности. Целесообразно рассматривать классификацию МР и МВО не по всей стране в целом, а по регионам, чтобы классы водных объектов попадали в один географический регион. Знание соотношений числа объектов в разных классах по регионам и их влияния на процессы в гидрологии и хозяйствовании ведет к формулировкам задач выбора объемов мероприятий на малых водных объектах в регионах и очередности осуществления мероприятий. Предотвращение деградации малых водных объектов, предотвращение их исчезновения, восстановление и поддержание в надлежащем состоянии малых водных объектов - это работа по сохранению природы и достойных условий жизни в ней человека.

Методология классификации малых водных объектов. Определение классов водных объектов основано на рассмотрении совокупности системных аспектов, или факторов классификации . Системные аспекты (факторы классификации) [4] - это основные понятия дисциплин, имеющие отношения к изучению водных объектов: гидрография, морфология речной долины и русла, ландшафт, рельеф реки, гидрология стока, использование стока, антропогенная нагрузка, качество вод, экосистема реки.

Водный объект по каждому фактору-аспекту классификации описывается параметрами и характеристиками. Характеристики определяют качественное описание объекта и выражаются формализованными по семантике и синтаксису словами-обозначениями. Показатели отражают количественные (числовые) соотношения в описании объекта. Например, гидрография имеет характеристики равнинной, предгорной или горной реки, описывается показателями длины реки, площади водосбора, разветвленности (числом впадений на единицу длины, общим числом основных по крупности притоков), извилистости (коэффициентом извилистости реки). Морфология характеризует строение речной долины, наличие пойм, число террас (у малой реки чаще одна терраса); показатели морфологии включают в себя среднюю ширину пойм, коэффициент извилистости долины, среднюю ширину и глубину русла. Обычно ландшафт характеризуется по видам [8]:

• -    классу морфологической структуры (равнинный, горный, низменный),

• -    почвенному биотипу (лесной, лесостепной, степной),

• -    роду генетики рельефа (степной, равнинный, пустынный, мелкосопочный),

• -    виду литологии поверхности (песчаный, галечниковый, лёссовый).

Рельеф описывается значениями уклонов (максимальный, средний, минимальный), наличием особенностей (водопадов, порогов). Гидрология характеризуется изученностью и определяет годовой сток реки разной обеспеченности, фазы стока, тип питания, долю подземного стока, возможность и продолжительность ледовых явлений, а также показатели твердого стока. Характеристики гидрогеологии включены в вид ландшафта, они могут дополняться типом грунта ложа реки и толщиной основного слоя, состоянием топографии берегов. Важной характеристикой реки является «коэффициент антропогенного давления», установленный для территорий в зависимости от плотности населения [13]. Целесообразно распространить это понятие и на МР и МВО как показатель значимости реки (экономической, демографический, социальной, например, в эвристических баллах). Желательны общие показатели сброса загрязняющих веществ в реку и характеристика качества воды - класс качества. Загрязнения также могут характеризоваться классом опасности (токсичности) и оцениваются по пятибалльной шкале, а состав загрязнений принимаются по типовому составу сточных вод [3, 10]. Использование стока описывается коэффициентом зарегулированности [9] и числом водохранилищ на реке. Экосистема реки характеризуется географическим положением, что отражает климат, и продуктивностью биоценоза [14]. Мы привели здесь главные характеристики и параметры факторов классификации МВО, более полный их состав подлежит детальной разработке при создании автоматизированной системы маломасштабных водных объектов. Везде есть качественные характеристики и числовые параметры.

Получить информацию о МР и МВО можно по картографическим материалам, ежегодным гидрологическим наблюдениям, географическим источникам. Используя все возможности получения информации, надо иметь в виду, что информация по отдельным разделам может быть не полной, точность низкая. При неопределенности и приблизительности данных ориентируются на сходные условия рек-аналогов и соображения эвристики, отсутствие данных по некоторым разделам, если их немного, не препятствует классификации объекта. При выборе представителя из множества малых рек имеется в виду, что МВО других видов (водоемы, болота, подземные воды) находятся в бассейнах малых рек, так что состав, характеристики и показатели малых водных объектов отражаются в их классификации малых рек.

Формализация выделения классов маломасштабных водных объектов. При классификации рек с определением близости между ними сравниваются отдельные реки с присущими им характеристиками по факторам классификации. Поскольку количество и типы притоков отражены в полных характеристиках сравниваемых рек, при классификации сравниваются, таким образом, и бассейны этих рек в целом.

Пусть r , р = 1, R - нумерация речных систем; g - порядок реки в данной проблеме классификации рассматривается обратный принятому в гидрографии порядку притоков. Конкретно: если самый маленький водный объект - это ручей без притоков, для него g=1, тогда в речушку порядка g =2 впадают только ручьи, вообще река r порядка g r представляет собой водоток, в который впадают только реки р порядка g p < g r .

При классификации сравниваются однородные части рек, которые на всем своем протяжении имеют схожие морфологию, топографию, ландшафт и пр. характеристики, но многие реки достаточно длинные, условия меняются по длине. Как правило, длинная река имеет три части: исток и верховье, среднее течение, низовье. Есть два пути классификации таких рек. При определении близости можно анализировать реки по комплексной характеристике, включая все три части, рассматривая реки как целостные объекты классификации, но можно рассматривать реку как нижнюю часть с притоком средней части, в которую в свою очередь впадает приток - верховье реки.

Распределение по классам основывается на сравнениях водных объектов друг с другом по характеристикам и параметрам их описаний в разных системных аспектах (факторах классификации). Пусть s = 1, S - нумерация аспектов классификации, C = {C 1,C2,...Cs...CS} - совокупность наборов характеристик по всем аспек- там классификации, P = {P 1, P2.... Ps... PS }

—

совокупность наборов параметров. Каждая характеристика    s -го   аспекта   есть набор

^P = { Р 1 , Р 2 ,... Р п ,... P Ns }

Важнейшим инструментом операций по классификации МР является мера близости двух водных объектов по составу их характеристик и параметров. Пусть L C , _р - мера близости характеристик г -го и р -ио объектов, а L. , _р - мера близости их параметров. Определим меру близости по параметрам:

_P        S       N _s

Lr, р  X s =1^s X n =1Пп f s Рг

—

Р р т

( p s + Р р )

где o_s - коэффициент предпочтения (значимости) системных аспектов, а ^П П - коэффициент предпочтения п -го параметра в s -м аспекте. При этом величины o_s и ^П П нормированы, т.е. X _s ■ ^ = ¹ и X N X = ¹. Тогда о <  L ^p , р <  1.

Мера близости характеристик двух объектов есть сумма близости по аспектам классификации с нормированными коэффициентами предпочтения (значимости) m-х характеристик в s Ms s s-м аспекте лт , где Xm=1nm =1:

L = Vs а УМ П х Ds(ds ,ds )

^г , ^р     S = 1s = 1 ^s ^^m = 1 ^m          m r^{5 m} p '

При этом для каждого аспекта - фактора классификации определена мера близости пар характеристик

D ( d m, , d m р ) = / р d , d m р , s = 1, 5 ; т г , т р = 1M ] по соответствующей таблице сравнений D s , вид которой приведен ниже в решении примера классификации малых рек Ярославской области.

Полная оценка близости двух объектов г и р есть взвешенная сумма:

L r , р = Y c ^х L C , р ⁺ Y p ^х L ^p , р ; Y c ⁺ Y p = ¹       (₃)

Близость объектов изменяется от 0 до 1, ⁰ <  ^L _г , _р <  1 . При этом L =0 означает идентичные объекты, L =1 - максимально несхожие объекты.

Нормирование величин сравнения параметров достигается путем отношения разницы их значений к сумме параметров, как это дано в (1). В отношении сравнения характеристик - в соответствующих таблицах сравнений указывается близость разных характеристик одного системного фактора классификации, и эти величины уже должны быть нормированы, т.е. лежать в пределах от 0 до 1. При определении полной близости по всем факторам классификации нормирование сохраняется, поскольку коэффициенты предпочтений нормированы, т.е. в сумме равны 1. Целесообразно за меру близости принять евклидову меру, как это показано в формуле (1) в отношении параметров; в отношении характеристик в таблицах сравнений необходимо обеспечить по всем столбцам и строкам аппроксимацию зависимостей близости выпуклой функцией. В евклидовой мере схожести существует свойство треугольника по соотношениям близости попарно трех водных объектов г 1 , г ₂ и г з - L n, г ₂ ^{+ L} г ₂ , г ₃ ^ L , , г ₃ . Для выявления групп водных объектов, основанных на соотношениях близости, евклидова мера близости целесообразно, оставляя нас в рамках привычной геометрии.

Определение близости водных объектов является необходимым условием распределения заданного их числа на классы схожести, характеризующиеся величиной максимально допустимой близости L _max. Назовем группой схожести объектов такую их совокупность G , которая характеризуется близостью не выше заданной L _max для любой пары объектов этой совокупности, т.е. группы объектов. Формально можно записать группу как G = { г: V г. г е G , L <  L }

V 1 , 2 , г 1 ,г 2 max )•

На множеств е в сех рассматриваемых водных объектов г = 1, R можно выделить много групп схожести G , в зависимости от того, с какого объекта начинать строить группу. Водный объект ρ , с которого начинается построение группы, назовем базовым объектом, группу -базовой, в обозначение ее введем номер базового объекта и значение критерия близости, G ( p , L _max). Для построения группы G(p , L _max) достаточно перебрать г = 1,.. R , г ^ р с отбором объектов, близких к р и другим объектам строящейся группы.

В рамках автоматизированной экспертной системы действия вычислений близости водных объектов, выделения групп и классов схожести используют определенные расчетные процедуры. Процедуру вычисления оценки близости

L1, r ₂ двух водных объектов r 1 и r ₂ обозначим как П 1 ( r 1 , r ₂). Процедура кропотлива, включает вычисления близости по параметрам и характеристикам, поиск в таблицах сравнений, учет отсутствия в рассматриваемых объектах некоторых данных. Когда из-за недостаточной изученности водных объектов не определена та или иная характеристика или параметр, при вычислении близости объектов интуитивно принято, что близость сравниваемых объектов по данной характеристике или параметру есть, но невысокая (0,2-0,3).

Построение базовых групп не однозначно. Групп G(p L max ), привязанных к водному объекту ρ , можно построить много. Если при построении группы, начиная от р , найдутся объекты r 1 и r ₂, близкие к р ^, L p , r 1 <  ^L max и L p rr 2 <  ^L max , но друг ^от друга далекие L_rb r 2 >  L max , то в G(p,L max ) можно включить r i , но не r ₂, или включить r ₂, а не r 1 , образуются две группы G 1 ( р L max ), G 2 ( p L max ), (рис. 1).

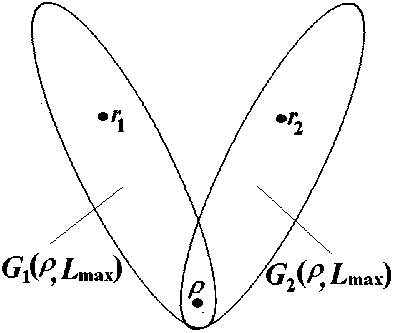
Рис. 1. Множественность групп водных объектов с одним базовым p , критерий близости L m _ax

Построение любой группы можно продолжать до исчерпания всех водных объектов, близких к р и другим уже вошедшим в группу объектам. В таком смысле группа «максимальная», т.е. содержит максимально возможное число водных объектов, которых можно включить в группу. Если построить все максимальные группа схожести GАр ), G₂(р ), G ₃( р )... с одним базовым водным объектом р , то в каждой паре групп есть несхожие друг с другом объек^ты, т.е. Г 1 G G 1 ( p ), r ₂ G G ₂( p ) , ^но L r ₂ >  ^L max ^, поскольку в одной группе могут превалировать одни близкие характеристики и параметры, а в другой группе другие.

То, что при сравнении близости объектов с заданным критерием допустимой близости Lmax, например, для трех МВО r 1, r2 и r3, может оказаться, что L гз > Lmin , хотя Ц,r < Lmin и L < L , объясняется тем, что схожесть меж-r2, 'з        min ду rj и r2 может быть основана на близости параметров и характеристик одного фактора, а схожесть между r2 и r3 - на близости параметров и характеристик другого фактора, но сами факторы могут быть достаточно далеки друг от друга, что и проявляется в сравнении r 1 с r3 и вычислении близости между ними.

Например, пусть одна река r 1 - равнинная, небольшой длины, небольшой площади водосбора. Другая река r ₂ - также равнинная, но длинная, хотя и с небольшой площадью водосбора. Третья река r ₃ - предгорная, небольшой длины и с небольшой площадью водосбора. При сравнении r 1 с r ₂ близость их друг к другу обеспечивается том, что обе реки равнинные и небольшой площади водосбора. Близость r ■ с r ₃ обеспечивается тем, что сравнимы длина рек и площади водосбора, хотя одна река равнинная, а другая предгорная. Однако реки r ₂ и r ₃ далеки друг от друга, поскольку два показателя из трех отличаются друг от друга: равнинная и предгорная, длинная и короткая, - только площади их водосборов сравнимы. Данный пример, хотя имеет общий характер без вычислений, иллюстрирует сам принцип сравнения близости.

Усилим требования к группе схожести. Пусть проводится построение группы водных объектов

^{G (} P ^{, L} max ) = ^{{ r :} L p , r <  ^L max ;

,

V r, r2 g G ^ Lr r < Lm ' 1y 2               г,r       max v содержащей максимально возможное число близких к р объектов. Но не будем включать в группу G объекты r1,r2 которые в отдельности могли бы войти туда, поскольку близки к базовому объекту р и к другим уже вошедшим в группу объектам, но сами далеки друг от друга Lr 1,r2>Lmax. В G не включаются ни r 1, ни r2 вместе. Такой «скупой» отбор объектов как бы минимизирует их число. Поэтому назовем группу водных объектов с базовым р и критерием близости Lmax совокупность с максимально возможным числом объектов rn=1,2,^, близость которых к р и попарно друг к другу меньше Lmax, Lp,rn < Lmax, Lr ] r 2 < Lmax и выполнением условия: водные объекты ri и r2, близкие к р, т.е. L .< L и p,r 1       max

^Lp , r ₂ <  ^L max , но далекие друг от друга L r , r ₂ >  L _max , - оба, r ■ и r ₂ не входят в минимальную группу, - минимаксной группой с обозначением G .

^p , ^L max

Относительно минимаксной группы Gρ,L выскажем следующее.

Утверждение 1 . Минимаксная группа водных объектов с базовым объектом ρ по критерию близ ост и L max выделяется на множестве МВО r = 1, R однозначно.

Доказательство. Если бы существовали две минимаксных группы МВО, привязанных к водному объекту ρ по критерию близости L max , (см. рис. 2), то одна из них G `    лежала бы целиком

ρ,Lmax в G1(ρ, Lmax), а другая G``     - в группе

ρ , _max

G ( ρ , L ) . Нашлись бы два объекта, принадлежащие порознь этим группам, т.е. r ₁ ∈ G ` <sub>ρ , L</sub> , но r ∉ G ``     , и r ∈ G ``     , но r ∉ G `     . Это

• 1            ρ , L _max              2            ρ , L _max              2           ρ , L max

значит, что r 1 , r 2 далеки друг от друга, L r ₁ , r ₂ > L max , противореча правилу строения минимаксной группы.

Следствие. Минимаксную группу с базовым МВО ρ и критерием L max можно определить как пересечение всех групп с базовым ρ : G = Q G ( p ,L ).

ρ , L _min             n , max .

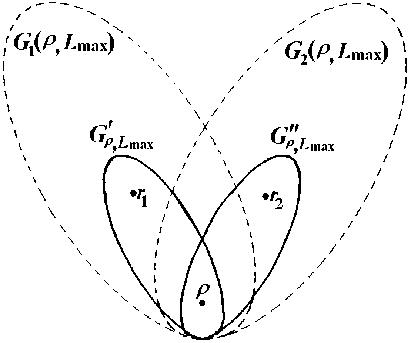
Рис. 2. К доказательству однозначности выделения минимаксной группы водных объектов по критерию близости L max с одним базовым водным объектом ρ

Можно усилить свойства минимальной группы объектов утверждением:

Утверждение 2. Минимаксная группа объектов по критерию близости L max инвариантна относительно всех входящих в группу водных объектов, т.е. минимаксная группа выделяется на множестве объектов r = 1, R однозначно, какой бы объект ρ , входящий в группу ни взять в качестве базового объекта, к которому эта минимаксная группа привязана ρ ∈ G _{ρ , L} .

Доказательство. Достаточно показать, что две минимаксные группы Gρ ,L и Gρ ,L , привязанные к разным объектам ρ1 и ρ2, не могут пересекаться: они либо полностью совпадают, либо не содержат ни одного общего объекта. Действительно, если две минимальные группы пересекаются, как на рис. 3., то существуют водные объекты r ∈ G и r ∈ G , но 1         ρ1 , Lmax                2         ρ2 ,Lmax r ∉ G        и r ∉ G , а также

• 2         ρ ₁ , L _min                          1         ρ ₂ , L _max

r e G p l Q G p l .       При       этом

• 3         ρ 1 , L max          ρ 2 , L max

L ≤ L ,L ≤ L , водный объект r бли-r1 , ρ1        max ρ2 ,r2       max зок ко всем другим водным объектам рассматриваемых минимальных групп - ρ1,r1 , ρ2 ,r2 , -Lr3,ρ1, Lr3,ρ2, Lr3,r1, Lr3,r2 ≤ Lmax. Если теперь рассмотреть пару ρ1 и r2, то должно быть L > L , иначе r вошло бы в G . Но то-ρ1 ,r2        max                                                 ρ1 ,Lmax гда с точки зрения построения группы Gρ ,L объект r2 не должен входить в Gρ ,L , поскольку при L ≤ L и L ≤ L , однако, ρ1 ,r3        max                    r2 ,r3        max

L _{ρ ,r} >  L_miax , что противоречит правилу построения минимаксной группы¸ в G _{ρ ,L} не должны входить как объект ρ 1 , так и водный объект r 2 . Аналогично доказывается невозможность ситуации, изображенной на рис. 3., если рассмотреть пару объектов ρ 2 и r 1 . Таким образом, возможно либо полное совпадение групп G _{ρ ,L} и G _{ρ ,L} , либо полная « самостоятельность » этих групп. Доказательство не меняется, если один из объектов ρ 1 или ρ 2 находится в пересечении минимальных групп G _p , L^ Q G _p , L_mi , - в таком случае доказательство повторяет утверждение 1.

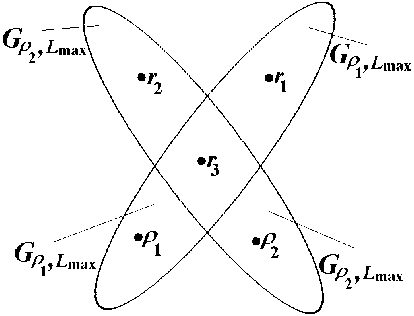
Рис. 3. К доказательству однозначности выделения минимаксных групп водных объектов

Следствие. Минимаксная группа Gρ,L выделяется на множестве водных объектов однозначно независимо от того, с какого объекта ρ начать ее построение. Можно последовательно выделять минимаксные группы на всем заданном множестве МВО r = 1,R , перебирая объекты ρ, которые еще не вошли в построенные группы, и такое разбиение множества МВО однозначно.

Минимаксные группы МВО, выделенные по критерию близости Lmax, и есть классы водных объектов, в каждом из которых выбирается далее типовой водный объект, подлежащий детальному изучению. Понятие класса водных объектов и требования к разбиению всего множества объектов на классы определено во Введении. Будем обозначать классы водных объектов как С*     с указанием центрального (типо- rcntr ’•‘■'max вого) водного объекта rcntr в классе и критерия близости Lmax. Объект rcntr отвечает условию

L = min rcntr , r еС rcntr ’ r                    .

Расчетная процедура П ₂ ( р , L _max ) как алгоритм построения минимаксной группы G -класса МВО С , , начиная с р записывается:

' cntr ^{- L} max

• 1.    р >  G { р ,..} , где G - список номеров водных объектов искомой группы.

• 2.    Цикл 3-9 по объектам еще не вошедшим в G:

• 3.    Вычисляется оценка близости L _р , _r объектов р и r по процедуре П 1 ( р , r ) ;

• 4.    Если L <  L , - то выполняется блок вы- р , r       max

• 5.    Цикл 6-7 по всем водным объектам в строящейся группе r * е G , r * ^ р ,

• 6.    Вычисляется оценка близости L * объектов r , r

r е 1, R , r * р , r t G .

числений 5-8:

• r , r процедурой П 1 ( r , r * ) ;

• 7.    Если L . >  L ^r и ^r выбрасываются из r , r        ^max-

• списка G, переход п.10;

• 8.    Переход к п.6 со следующим объектом r * = r * + 1 ; если же все объекты списка G строящейся группы исчерпаны, переходим к п.9;

• 9.    Объект r записывается в список G = { р ,.., r } группы, далее п.10;

• 10.    Переход к п.3 со следующим объектом r = r +1 цикла 2-10;

Процедура П ₂( р , L _max) заканчивается с концом перебора объектов r е 1, R .

Из данного выше определения класса схожести водных объектов, приведенного алгоритма П ₂( р , L _max) , а также свойства однозначности выбора классов при заданном L max независимо от выбора базового объекта этого класса, можно предложить процедуру п ( L _m) полного разбиения множества водных объектов r е 1, R на классы схожести по мере близости L max :

• 1.    В процессе классификации заполняется матрица распределенных по классам объектов ^M\ k , ^r ||, где в k -ой строке матрицы описывается k -й класс путем перечисления входящих в него объектов r . Вначале матрица пустая, M =0.

• 2.    Выбираем любой объект р _е 1, R , р t M , если р не нашлось, т.е. все объекты уже распределены по классам, процедура П ₃( L _max) заканчивает свою работу.

• 3.    Выполняется процедура П ₂( р , L _min) построения класса объектов (см. выше) с базовым объектом ρ ; классу присваивается порядковый номер k = k +1, и его состав перечисляется в k -й строке матрицы M . Переход к пункту 2.

Наконец, процедура П ₄( k ) определяет в классе водных объектов, заданном по строке матрицы M , центральный объект r cntr по условию минимума суммы близости его ко всем объектам класса. При проведении самой классификации объектов была уже построена матрица расстояний L ( r 1 , r ₂) , всевозможных пар объектов, процедуру П ( k ) достаточно выполнять прямым перебором объектов заданного класса с выбором объекта с минимумом суммы оценок близости. Этот центральный в классе объект принимается за типовой.

Выбор критерия классификации МВО. Пусть K ( L _max) - число классов рек, зависящее от принятой допустимой близости объектов L max . На рис.4 дан график классификации некоторых пяти рек при разных значениях L max . В общем случае зависимость числа классов от меры близости объектов K ( L max ) можно построить практически, многократно выполнив трудоемкую при огромном числе водных объектов классификацию. Значения близости объектов друг к другу дискретны, поскольку число водных объектов конечно, хотя многочисленно. Дискретно и число классов K =1,2,... R , поэтому функция K ( L _max) ступенчатая. Критерий классификации водных объектов L max можно задавать непрерывно от 0 до 1. При L max =0 ни один объект не схож ни с каким другим, всегда L > L _max, и число классов равно числу самих объектов K = ^R . При L _max=1 все объекты схожи, для всех пар L < L _max, разницы между объектами не выявляется, все они входят в один класс, K =1.

Возникает проблема выбора определенного значения Loptmax, которое должно быть установлено для проведения классификации водных объектов. Здесь, с одной стороны, необходимо определить достаточное число классов водных объектов, рассматривая тесно схожие между собой объекты в каждом классе, но с другой стороны, не увеличивать чрезмерно число этих классов, так, чтобы вся работа по анализу типовых объектов этих классов была бы обозрима. Искомое значение близости в определенном смысле лучшее (оптимальное).

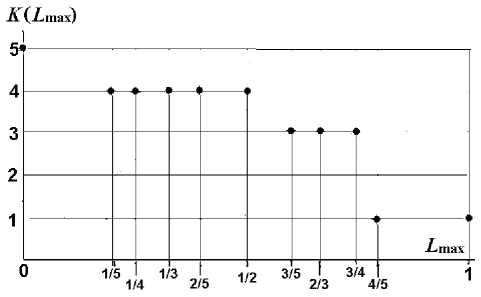
Рис. 4. График функции K ( L max ) числа классов условных рек

Принцип обоснования значения L max исходит из оценок затрат Z k на обработку выбранных типовых объектов выделенных классов k= 1, К в сумме с оценками дополнительных затрат Z^r k на привязку решений по каждому нетиповому водному объекту класса k , и так по всем классам. Следует определить число классов водных объектов при минимуме суммы Z=Z k +Z^r k . Однозначно формализовать определение L max не удается, но при приемлемых допущениях можно получить достаточно простой и удобный результат. Заметим, что стоимость z k детального изучения типового объекта любого k -го класса и планирования водных мероприятий по его сохранению и улучшению определить невозможно, также как невозможно точно определить стоимость z^r k переноса результатов этого изучения на нетиповой водный объект k -го класса. Перенос данных с типового не нетиповой водный объект использует принцип подобия в определении створов, расстояний, объемов, других свойств и показателей нетипового объекта. Последовательность действий по переносу данных с одного объекта на другой схожий объект можно детально описать с необходимой для этого подробностью.

Допустим, что затраты z k на изучение типового водного объекта равны для всех классов объектов, т.е. z k =const, так как набор действий по сбору данных, проведению нужных расчетов и пр. типового водного объекта почти одинаков для всех объектов. Затем можно принять аппроксимацию числа K классов от величины L max , изображенной на рис. 4., линейной зависимостью:

L max

( R - к V

/( R - 1)

Примем зависимость стоимости переноса результатов изучения типового объекта на нетиповые объекты в одном классе линейной от близости объектов со стоимостным коэффициентом σ k :

z^rr = CT x L kk

Действительно, затраты переноса z^r k тем выше, чем больше отличий водных объектов в классе от установленного там типового объекта, т.е. чем шире состав каждого класса. В среднем в каждый класс входит R / K объектов, из них нетиповых ( R – K )/ K . Сами же величины z k , z^r k установить невозможно. Примем σ k =const для любого класса k. Примем также, что в каждом классе нетиповые объекты распределены равномерно по расстоянию близости от типового объекта между 0 и L max , и среднее в (5) L = L max /2. Наконец, σ = σ k /2=const для всех классов водных объектов. Тогда из (5) среднее значение стоимости переноса на один нетиповой объект в любом классе:

z^r r = ct x L k           max

Сумма затрат на изучение типовых водных объектов всех классов и перенос результатов на нетиповые объекты, учитывая (4), (6) и среднее число нетиповых объектов в классе:

Z = Z k K + ст x ( R - K ) 2 /( R - 1) =     (7)

= z_k [ K + ст / z_k x ( R - K ) 2 /( R - 1)]

Изучим теперь соотношение σ/zk<1 стоимости переноса результатов на нетиповой объект σ к стоимости изучения типового объекта zk. Можно полагать, что σ/zk = γ/K, где γ=const. Действительно, σ зависит от принятого Lmax и от числа K объектов, поскольку процедура переноса результатов усложняется при увеличении различий между типовым и нетиповыми объектами. При Lmax=1 все водные объекты входят в один класс, K=1, стоимость переноса результатов от единственного типового объекта ко всем остальным велика и равносильна самостоятельному исследованию каждого объекта, откуда σ =zk, Y=1. При L = 0 все или почти все объекты не-max схожи друг с другом, число классов K = R необходимость в переносе результатов пропадает или осуществляется на очень схожие с типовыми объекты, стоимость переноса мала или нулевая, снова можно принять γ=1, так как при этом σ/zk= 1/R – очень мало. Допустив линейное изменение γ при изменении Lmax от 0 до 1, как принята линейность в (4), (5) и (6), констатируем γ=1 при любом Lmax. Отсюда (7) перепишется:

z = z_k

K + (R - KL

K ( R - 1)

^ min

Найти минимум Z в непрерывном случае не представляет труда, он равен:

K

opt

R

Оптимальное число классов принимается как ближайшее целое. Вывод (9) основан на допущениях, но результат соответствует экспертной оценке. Если провести рассуждения не со стоимостями изучения типовых объектов и переносом результатов на нетиповые, а с возникающими погрешностями и минимизировать сумму погрешностей по всем классам, снова получаем (9). Однако, определив Kopt, не так просто определить соответствующую меру близости Lopn , которая должна быть принята для классификации. Без непосредственного выполнения классификации объектов с применением процедуры П3(Lmax) не обойтись. Можно использовать одномерный поиск оптимума Фибоначчи [12], но можно воспользоваться следующей процедурой. Вначале зависимость K(Lmax) определена только для граничных значений: K(0)=R и K(1)=1. Предположив для первого приближения K(L)=R - (R - 1)L (рис. 5) и положив отсюда L '= (R - Kopl) /(R -1), выполним процедуру П3(L') классификации и определим для L' фактическое значение числа классов K'. Ищем положение Kopt на уточненной зависимости K(Lmax). Пусть K'> K opt и Lop^ лежит на отрезке L ^Lmax . Во втором приближении предположив K (L) = [(K '-1) L + L'-K']/(L '-1), и опреде- лив отсюда

L' = [( L ' - 1) х K_opt - L ' + K ')]/( K ' - 1) , снова выполним классификацию и т.д. Процесс быстро сходится к L op in при K opt .

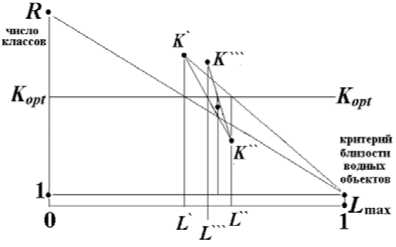
Рис. 5. К алгоритму поиска L opt n по заданному числу классов K opt

Пример классификации МВО. Ниже в табл. 1 даны основные характеристики и параметры 65 рек Ярославской области среднего и небольшого размера, по совокупности которых далее проведены процедуры их классификации. В табл. 2 даны установленные оценки близости отдельных характеристик и параметров водных объектов, используемые для классификации этих рек. В табл. 3 приведены классы рек и оценки близости рек друг с другом. В пределах Ярославлской области насчитывается 4327 водотоков, причем 3696 составляют ручьи и очень маленькие речки, длина которых не превышает 10 км. 245 речек имеют длину от 11 до 20 км, 64 реки - от 21 до 50 км; 18 рек - от 51 до 200 км, наконец, 11 относительно крупных рек имеют длину от 101 до 150 км. Большинство рек несут свои воды в Волгу, являясь ее притоками или притоками ее притоков. Несколько рек впадает в озеро Неро и Плещеево озеро. Истоки всех рек находятся на высоте от 100 до 290 м над ур. м. Падение их русла на каждый километр составляет от 7 до 12 см, что характерно для рек равнинного типа. Течение таких рек, как правило, плавное, спокойное, берега порастают осокой. Часть мелких речек летом пересыхают, зимой промерзают до дна. Но во время весеннего снеготаяния или в период осенних дождей эти маленькие речки могут преобразиться, становятся полноводными, а более крупные реки нередко превращаются в бурные потоки, которые смывают на своем пути мосты и прибрежные постройки, рушат берега.

Каждый год в водоемы Ярославской области сбрасывается около 340 млн. м3 загрязненных сточных вод. Наибольший вред водным ресурсам сточными водами наносят предприятия ЖКХ и электроэнергетики. Состояние водных ресурсов является основной проблемой Ярославской области, поскольку р. Волга отнесена к водоемам качественного истощения. Еще проблема - подтопление городов области, оно сопровождается большими экологическими последствиями, которые приносят вред здоровью населения области. Реки в табл. 1 классификации, данные в алфавитном порядке, выбраны случайным образом, поэтому столь сильно различаются полнотой информации. Факторы классификации: гидрография, ландшафт и растительность, хозяйственная нагрузка. К параметрам относятся графы 3, 4, 5, 7, 8, 9, 12, 13, к характеристикам - 5, 10, 11. Приоритеты факторов классификации, параметров и характеристик внутри факторов показаны в строках таблицы.

Таблица 1. Реки Ярославской области

№ №	РЕКА	Длина км	Водосбор км2	Извилистость прямое / меандры / извили-ста/стари цы	Крупные притоки	Ширина, м	Глубина, м	Скорость течения км/час	Расти-тель-ность: лес, луг пашня, болото	Ландшафт возвыш равнина низина пойма	Население примерное число: деревни поселки города	Хозяйств. начение % экспертн. величина. отдельно судоходство
1	2	3	4	5	6	7	8	9	10	11	12	13
	Факторы	Гидрография, приоритет σ = 0.4							Ландшафт, σ = 0,3		Население, σ = 0.3
	Приоритеты π	0,35	0,20	0,25	0,1	0,05	0,05	0,05	0,5	0,5	0,5	0,5
1	Болжбина	13
2	Вандышка	33	150								5 нас.пнкт
3	Вёкса Которосль	7
4	Вёкса в Сомино	9		извилиста		20 -30	1,5	4		круто	2 поселка	60%
5	Верекса	54		извилиста					болото
6	Вогра	20	68,1
7	Вондель	31	133
8	Воргуша	6,8	12,5
9	Воржехоть	33	162		3						13
10	Воронуха	11									9 дер.
11	Глухая Репа	12
12	Жабня	58	323
13	Звениха	15	35,4
14	Золотуха	17									2 дер.
15	Ивровка	10
16	Ильд.	46	240
17	Ить	68
18	Ишня	17	131
19	Касть	99
20	Катка	57	493								Около 30
21	Кештом	48			1				лес		17	30%
22	Кисьма	29	136		2						21
23	Колокша	37	180		5				лес	болото	7
24	Корожечна	140			20					холмы	много
25	Коровка	23	177		24
26	Которосль	125				25-60	1,5-3		луг,лес	равнина, низина
27	Кострома	354				8–20 20-60	0,5-3		болота	долина низина	дер.села, 2 города	судоходна
28	Крекша	17	36								5
29	Кубрь	87	1009							возвыш		50%
30	Лама	139	2330	прямая	3	6 до 45	0,5-6		лес
31	Лахость	96		извилиста		5-15	1-4					50%
32	Лунка	37		пороги		узкая	мелкая			возвышн
33	Мимошня	22	52
34	Могза. .	87			2			6-8	лес	низина
35	Молокша	39						5-6	лес	болота		15%
36	Мошница	16	67
37	Нерль в Волгу	112	3610		5	35-75	1-4		болота	низина	7дер 3села	70%
38	Нерль в Клязьму	284	6780		4						15 нас.пнкт
39	Нора	6-7									В черте	Ярославля
40	Нотелга	32	169								1 дер
41	Обнора.	127			4-5	60			лес	равнина
42	Пахма	55	600	извилиста	7	20-30			поля лес		11	70%
43	Печегда	46	328		18,3кр	10-25-40			лес,болт			70%
44	Пукша	34	260		6						17	50%
45	Сабля	78									2села 5дер	40%
46	Сара	93	791	извилиста			мелкая			низина
47	Себла	60
48	Сить	158		извилиста	2				лес	равнина
49	Сога	64								низина
50	Согожа	125			9	60-80	6		лес	равнина		судоходна
51	Сольба	54		старицы					луга	низина
52	Солоница	132		извилиста					лес	равнина
53	Соть.	170			2	10-15			лес	возвышен.		30%
54	Сутка	84								низина

55	Трубеж	33	253			20-25	2,5			равнина
56	Туношна	51	448							низина
57	Устье в Кото- росль	153	2530		7	40-50	1,3-1,5		заросли	возвышен		30%
58	Уча (Обнора)	83
59	Ухра	126		извилиста	6	60-200	2	6-7	лес	возвышн		судоходна
60	Ухтома	88		извилиста					заросли	возвышн
61	Урдома	37	357
62	Улейма	83	732			15-20
63	Черёмуха	72	636								60/3/1
64	Шаха	46								болота
65	Юхоть	75	1700		5	8-10	1-1,5		кусты	равнина

Таблица 2. Коэффициенты близости водных объектов по характеристикам

Факторы классификации		Извилистость →	прямая река	меандры	извилистость	старицы
		Растительность →	лес	пашня	луг	болото
Извилистость ↓	Растительность ↓	Ландшафт ↓→	возвышен.	холмы	равнина	низина
прямая река	лес	возвышенность	0	0,025	0,1	0,225
меандры	пашня	Холмы	0,025	0	0,025	0,1
извилистость	луг	равнина	0,1	0,025	0	0,025
старицы	болото	Низина	0,225	0,1	0,025	0

Таблица 3. Варианты классификации малых рек

Классы рек при L max =0,6			Классы рек при L max =0,75			Классы рек при L max =0,9
Кла ссы	Реки	Описание	Кла ссы	Реки	Описание	Кла сы	Реки	Описание
1	2	3	4	5	6	7	8	9
1	Болжбина	L=10-13 км. Данных мало	1	Болжбина	L = 10-25 км F = 50-150 км2 По 2 – 3 деревни на реке Другой информации нет	1	Болжбина	L = 5-25 км F = 10-180 км2 Другой информации нет
	Глухая Репа			Глухая Репа			Глухая Репа
	Ивровка			Ивровка			Ивровка
2	Воронуха	L=11-20 км. F=30-40 км2 2-3-4 деревни Других данных мало		Воронуха			Воронуха
	Золотуха			Золотуха			Золотуха
	Крекша			Крекша			Крекша
	Звениха			Звениха			Звениха
	Вогра			Вогра			Вогра
	Ишня			Ишня			Ишня
3	Вандышка	L=30-35 км. F=150 км2 3-5 нас. пункта Других данных мало		Мимошня			Вёкса в Кото- росль
	Вондель			Коровка			Воргуша
	Воржехоть			Мошница			Мимошня
	Нотелга		2	Вандышка	L = 30-60 км F=150-300 км2 По 3 – 4 населенных пункта на реке Другой ин-		Коровка
	Кисьма			Вондель			Мошница
4	Вёкса в Кото- росль	L=6-7 км. F=12 км2 Др. данных мало		Воржехоть			Вёкса в Сомино
	Воргуша			Нотелга			Нора
5	Нора	L=7 км. В городе		Кисьма		2	Вандышка
6	Жабня	L=40-60 км. F=250-350 км2		Жабня			Вондель
	Ильд.			Ильд.			Воржехоть

	Себла	Др. данных мало		Себла	формации нет		Нотелга	L = 30-60 км F=150-500 км2 По 3 – 5 населенных пункта на реке Равнина, леса, болота Хозяйственное развитие от 10% до 70%
	Урдома			Урдома			Кисьма
7	Мимошня	L=15-25 км. F=50-180 км2 Других данных мало		Трубеж			Жабня
	Коровка		3	Которосль	L=100-140 км F =2000-3600 км2 Реки прямые, B<60 м, H<4 м Лес, равнина, луг, низина		Ильд.
	Мошница			Лама			Себла
8	Которосль	L=120-140 км. F=2000-2500 км2 Прямая, В <6 0 м, Н<4м, 3-6 км/ч, Лес, луг, равнина, низина		Обнора			Урдома
	Лама			Уча			Колокша
	Обнора			Согожа			Молокша
	Уча			Нерль в Волгу			Шаха
	Согожа		4	Вёкса в Которосль	L= 6 - 9 км F = 12 км2		Кештом
9	Лахость.	L=75-150 км В<15, Н<4 м Извилистость, лес, кусты, равнина Хоз.разв.=40%		Воргуша			Пахма
	Солоница			Нора			Печегда
	Сить			Вёкса в Сомино			Пукша
	Юхоть		5	Лахость.	L= 75-150 км B<15, H<4 м Извилисты, лес кусты, равнина, хозяйство ≈ 40%		Трубеж
10	Могза. .	L=90 км, мелкая F=800 км2, лес, извилиста, низина		Солоница		3	Которосль	L=75-150 км F=2000-3500
	Сара			Сить			Лама
11	Сабля	L=70-80км. F=600-700 км2, В<20, деревни,села,город Хоз.развитие 40%		Юхоть			Обнора	извилистость равнина, низина, лес, кусты, хоз развитие до 40%
	Улейма		6	Могза. .	L=80-90 км F =500-800 км2 Реки мелкие, Извилистые, Лес, равнина, низина, болота, луг, старицы		Уча
	Черёмуха			Сара			Согожа
12	Нерль в Клязьму	250-350 км.6000-7000км2, В=20-60 дер,села,грд.болот судоход,долина		Верекса			Лахость.
	Кострома			Сольба			Солоница
				Сутка			Сить
13	Нерль в Волгу	L=112км. 3600 км2		Туношна			Юхоть
14	Верекса	L= 50-80,400-500км2 извилисты, старицы, болота, луг, низина	7	Нерль в Клязьму	См. класс 12 в классификации слева		Нерль в Волгу
	Сольба			Кострома			Касть
	Сутка					4	Могза. .	L = 70-90 км F=500-700 км2 Деревни, села, города Низина, леса, болота, луга, старицы Извилистые, Хозяйственное развитие около 40%
	Туношна		8	Соть	L=50-150 км F =2500 км2 Возышенность, холмы, пороги, Лес, судоходство, хозяйственное развитие ≈ 30%		Сара
15	Кубрь	90-130км возвыш. извилистость, лес, судоход, Хоз.=50%		Устье в Кото- росль			Сабля
	Ухра			Кубрь			Улейма
	Ухтома			Ухра			Черёмуха
16	Соть.	L=150км.=2500км2 извилистость, лес, возвыш. Хоз.=30%		Ухтома			Верекса
	Устье в Кото- росль			Касть			Сольба
17	Вёкса в Сомино	L=9 км.		Корожечна			Сутка
18	Колокша	L=35-45км. F=200-250 км2 леса, болота, хоз.=15%		Лунка			Туношна
	Молокша		9	Ить	L=50-90 км F =600-700 км2 Низина, Деревни, села, город Хозяйственное развитие ≈ 40%		Ить
	Шаха			Катка			Катка
19	Ить	L=60-70км. 500км2 низина много деревень		Сога			Сога
	Катка			Сабля		5	Нерль в Клязьму	См. класс 12 левой классификации
	Сога			Кештом			Кострома
20	Касть	L=100 км.		Улейма
21	Кештом	L=50 км. лес, дер. хоз=30%		Черёмуха		6	Кубрь	L=90-150 км F = 2500 км2, Возвышен., извилистость лес, судоходные хоз развитие до 70%
22	Корожечна	L=140 км. Холмы	10	Колокша	L=35-55 км F =250-500 км 2 Низина, Леса, болота, извилистые Хозяйственное		Ухра
23	Пахма	L=35-55 км. Поле лес,500км2,хоз.70% болото,извилисты		Молокша			Ухтома
	Печегда			Шаха			Соть.
	Пукша			Пукша			Устье в Кото- росль
24	Лунка	L=37 км. пороги		Печегда			Корожечна
25	Трубеж	L=33 км. равнина		Пахма	развитие ≈ 50%		Лунка

Примечание: в таблице даны обозначения: L - длина реки, F - водосборная площадь, B - ширина, H - глубина

В таблице 2 даны коэффициенты схожести объектов по характеристикам.

Для ввода, обработки и хранения данных по малым рекам, а также проведения их классификации и решения проблемных задач создается автоматизированная экспертная система АЭС «Малая река». В рамках подготовки части системы «Малая река. Классификация» разработаны компьютерные программы вычисления оценок схожести рек SimilarityRivers, программа классификации рек RiverClasses, программа определения типовой реки в каждом классе -TypingRivers. Программы выполнены на языке

Pascal-7 (Программная система «Малая река» пока носит экспериментальный характер, нуждаясь в накоплении опыта эксплуатации и последующего расширения). Результаты применения программ для классификации представленных в табл. 1 рек даны в табл. 3.

В соответствии с (9) оптимальное число классов равно 8, что соответствует примерно среднему столбцу табл. 2 результатов классификации. Данный пример показывает важность любой информации по рекам помимо длины. Без этого разные реки попадают в один класс лишь по соответствию длин.

Проблемы малых рек. В заключение статьи остановимся на системном перечислении проблем МР и МВО, технических и экологических мероприятий по сохранению МВО и улучшению условий их жизни. Мероприятия намечаются по водным объектам каждого класса, которые приняты в качестве типовых. Планирование мероприятий на типовом водном объекте представляет собой оптимизационную задачу, устанавливающую технические и экологические мероприятия при минимуме затрат на их осуществление (капитальные затраты и эксплуатация) [2, 3, 10]. Выявленный состав мероприятий, их стоимость, степень улучшения состояния типового МВО распространяется на другие водные объекты рассматриваемого класса. Накопленные в автоматизированной экспертной системе результаты расчетов типовых объектов с распространением на все объекты каждого класса позволят решать задачи выбора рек для осуществления на них необходимых мероприятий возрождения и охраны.

Проблемы, возникающие на маломасштабном водном объекте, делятся на проблемы: существования самого объекта как такового, сохранения его морфологических характеристик, сохранения и улучшения внешних условий жизни объекта, улучшения качества воды, сохранения и улучшения экосистемы объекта [7, 11]. Угрозу существования водному объекту как таковому несет обычно строительства жилых, промышленных зданий, дорог и пр. Как правило, такие планы предусматривают поворот, спрямление, засыпку, помещение реки в подземный коллектор, перекрытие притоков и многое другое. Принципиально нельзя отрицать возможности прекращения существования маломасштабного водного объекта, но это должно быть согласовано с изменениями во всей системе МВО на большой территории; это самостоятельная проблема, решения которой должно использовать данные, накапливаемые в АЭС «Малая река».

Сохранения морфологических характеристик водного объекта связано с тремя видами изменений: эрозией и разрушением берегов, размывом русла, заилением и заносами русла. Необходимо выявлять естественные тенденции морфологических изменений и определять, где и в какой степени следует поддержать эти изменения, а где им противостоять. К техническим мероприятиям по сохранению морфологических характеристик относятся: укрепление берегов (мощение, залужение, габионные стенки, направляющие дамбы), расчистка и углубление русла (экскаваторами, земснарядами, промывкой русла), конструирование меандров, отсечение стариц и мелководий, устройство обводных каналов и временных спрямлений с регулированием пропуска высоких вод (требует строительства направляющих дамб и шлюзов).

Сохранение и улучшение внешних условий жизни объекта связано с проведением работ на примыкающих поймах, прежде всего залесение или залужение, обустройство водоохранных зон, мероприятий по борьбе с оврагами, рассредоточение сооружений сброса загрязнений в водный объект.

Улучшения качества воды связано с выявлением сбросов сточных вод, строительством очистных сооружений на примыкающих к реке предприятиях. Сохранение и улучшение экосистемы малого водного объекта состоит в восстановлении речной растительности и рыбных популяций. Это достигается улучшением мест оби- тания донных беспозвоночных и рыбы, строительством мелиоративных сооружений (участков для нереста, мелких гидротехничекских сооружений - отражателей потока, запруд, подпорных габионов, ловушек мусора, мощений, заграждений из горбыля, бревенчатых и щитовых навесов - прибрежных укрытий). К восстановлению речных экосистеми относятся работы по рекультивации земель после их постороннего использования. Проблемы наблюдаются при расположении малого водного объекта в городе, где затраты на восстановление, улучшение и поддержание в хорошем состоянии выше.