Методология определения исходных данных для стендовых испытаний датчиков системы воздушных сигналов в условиях обледенения

Метод обеспечения выполнения требований к работоспособности датчиков системы воздушных сигналов (СВС) в условиях обледенения изложен в работе [1]. Как показывает статистика, по причине обледенения летателвного аппарата (ЛА) происходит значительная часть лётных происшествий, поэтому учёт последствий обледенения необходим ещё на. этапе проектирования и проведения лётных испытаний ЛА. Отрицательное влияние обледенения может проявляться как на. изменении аэродинамических характеристик (АДХ) ЛА, так и на. ухудшении функционирования СВС из-за. неправильных показаний обледеневших датчиков полного давления, статического давления, а. также датчиков аэродинамических углов. Стремление повысить безопасность полетов привело к выпуску новых сертификационных документов FAA (Федеральное управление гражданской авиации США) и EASA (Европейское агентство по безопасности полетов), ужесточающих требования к ЛА и их системам. Особое внимание к работе датчиков СВС стало уделяться после катастрофы самолета. А-330, AF447 в 2009 году. Анализ показал, что первопричиной её явилось обледенение всех датчиков полного давления. Это привело к активизации действий EASA по внедрению более жестких требований к условиям обледенения, при которых должна обеспечиваться устойчивая работа, датчиков СВС для вновь сертифицируемых самолетов, определённых Certification review item (CRI) F-05 (Flight Instrument External Probes - Qualification in

Icing Conditions, EASA, 2007). Для удовлетворения сертификационным требованиям эффективность обогрева датчиков и их работоспособность должны быть продемонстрированы в стендовых испытаниях при условиях обледенения. Причем, если сертификационные требования задают лишь внешние условия среды («матрицу облачности»), то в стендовых испытаниях каждый датчик должен быть испытан в условиях, соответствующих локальным параметрам набегающего потока в месте его установки на самолете. Таким образом, уже на ранних этапах проектирования самолёта при выборе мест расположения датчиков, кроме требований к точности показаний СВС, должны учитываться дополнительные требования по устойчивой работе датчиков в условиях обледенения [2].

Устойчивая работа датчиков СВС в условиях обледенения обеспечивается в первую очередь эффективным обогревом датчиков. Однако при использовании стандартных датчиков на различных ЛА могут возникать определенные трудности с обеспечением их требуемой работоспособности во всём эксплуатационном диапазоне изменения параметров. Это связано, в основном, с особенностями геометрии конкретного ЛА. Ужесточение требований к работоспособности датчиков СВС в условиях обледенения в первую очередь затрагивает внешние атмосферные условия. Вводимая CRI F-05 «матрица облачности» (табл. 1), устанавливает нижние границы 10 состояний, описывающих встречающиеся типичные облака, полёт в которых может привести к образованию льда на датчиках СВС.

Таблица 1

Матрица облачности CRIF-05

Test #	Cloud Type	SAT (°C)	Droplet LWC (g/m3)	Crystal LWC (g/m3)	Droplet MVD fpm)	Crystal MVD (pm)	Time duration (min)
L1	Liquid Phase Icing (supercooled droplets)	-30	0.2	0	20	0	15
L2	Liquid Phase Icing (supercooled droplets)	-30	1.1	0	20	0	5
L3	Liquid Phase Icing (supercooled droplets)	-20	1.85	0	20	0	5
L4	Liquid Phase Icing (supercooled droplets)	-10	2.5	0	20	0	5
Ml	Mixed Phase Icing (crystals/ supercooled droplets)	-10	1	4	20	1000	5
SI	Solid Phase Icing (crystals)	-35	0	2	0	1000	15
S2	Solid Phase Icing (crystals)	-35	0	5	0	1000	5
RI	Rain (droplets)	-2 toO	2	0	1000	0	15
R2	Rain (droplets)	-2 toO	6	0	2000	0	1.5
R3	Rain (droplets)	-2 toO	15	0	2000	0	0.33

Для приведенных условий полёта должна быть продемонстрирована работоспособность датчиков в сертификационных стендовых испытаниях. Причем в «матрице облачности» величина водности приведена для набегающего потока «на бесконечности», а не в зоне расположения датчика. Локальная водность, в зависимости от места расположения датчика, должна быть определена для каждого датчика для всех режимов испытаний. Таким образом, для каждого датчика полного давления и датчика аэродинамических углов расчётом требуется определить относительную водность потока в месте его расположения на самолёте для режимов стендовых испытаний датчика в условиях обледенения. Расчёт относительной водности выполняется при нулевом угле скольжения на режиме, когда местное число Маха и локальный угол атаки датчика (с учётом угла его установки) равен потребному для стендовых испытаний. В табл. 2 приведен типовой набор для стендовых сертификационных испытаний. Для датчика аэродинамических углов рассматривается только вариант АоА = 0°.

Таблица 2

Таблица сертификационных испытаний

м	АоА	MVD (pm)
		20	40	1000	2000
0.3	0°	+	+	+	+
	20°	+	+	-	-
0.5	0°	+	+	+	-
	10°	+	+	-	-
	20°	+	+	-	-
0.65	0е	+	+	+	-
	10°	+	+	+	-
	20°	+	+	-	-

Задача определения локальной водности разбивается на два этапа. На первом этапе для каждого датчика определяются параметры набегающего потока, соответствующие локальным параметрам потока сухого воздуха в районе датчика. Локальные параметры потока, в свою очередь, задаются исходя из условий сертификационных стендовых испытаний. Для этого проводится серия параметрических расчетов и строятся аппроксимационные зависимости M^(M_loc, АоА[_ос), AoA^(Mi_oc , AoAioc) по методике, описанной ниже. На втором этапе проводятся повторные расчеты сухого воздуха по параметрам, полученным из аппроксимационных зависимостей и по ним определяются локальные параметры водности для каждого датчика.

2.    Определение исходных параметров набегающего потока

Определение локальных параметров по результатам расчета. Расчеты локальных полей течения воздуха проводились по программе [3,4]. Программа основана на методе конечного объема, реализованного на неструктурированной расчетной сетке второго порядка точности. Используются уравнения RANS, замкнутые моделью турбулентности Спаларта-Аллмараса с учетом шероховатости. На втором этапе определяются значения локальной водности. Расчеты проводились по программе [10,11], основанной на решении системы уравнений водности. В качестве ЛА рассматривается модель CRM (NASA Common Research Model) без мотогондолы. Сетка загружена с сайта NASA. Размах крыла модели составляет 59 м. Сетка неструктурированная, количество ячеек 7618735 (рис. 1).

Рис. 1. Расчетная сетка, модели CRM

В рамках предлагаемой методологии возмущение поля от датчиков не учитывается, поэтому расчеты проводятся на геометрии, не учитывающей форму датчиков. Рассматривается два типовых датчика с типовым расположением на модели CRM. Первый — датчик полного и статического давления на державке высотой 15 сантиметров. Типовое расположение — на расстоянии 1 метр от носика фюзеляжа в верхней его части. Вторым является датчик аэродинамических углов. Он расположен на расстоянии 12 метров от носика фюзеляжа в центральной его части. Второй датчик представляет собой крылышко, расположенное перпендикулярно поверхности фюзеляжа длиной 10 сантиметров (рис. 2).

Рис. 2. Носовая часть фюзеляжа, и внешний вид датчиков

Место расположения датчиков и их характеристики задаются тремя параметрами: координатой точки расположения, направляющей вдоль датчика и вектором нормали к поверхности ЛА (табл. 3).

Таблица 3

Координаты и направление датчиков

	Расположение датчика, X , метры	Направление датчика, L	Нормаль к поверхности ЛА, N
Датчик полного и	3.382697	-0.866146	-0.532579
статического	0.813213	-0.472591	0.724009
давления 1	5.705340	-0.162631	0.438376
Датчик	14.14379	-1.0	0.0
аэродинамических	3.097969	0.0	0.997327
углов 2	5.616963	0.0	-0.073065

Локальные параметры потока для каждого датчика вычисляются путем интерполяции по рассчитанным полям сухого воздуха, в точку расположения датчика, (координаты даны ^

во второй колонке табл. 3, X). Тангенс локального угла атаки вычисляется как отношение проекции вектора, скорости на. нормаль к плоскости датчика, к вектору скорости по направлению датчика. Плоскость датчика задается векторами L и N (третья и четвертая колонки табл. 3 соответственно).

Построение аппроксимационных зависимостей

М \L, АоА^),АоА_ІОС(М^ , АоА^.

Значения локальных газодинамических параметров в районе расположения датчиков СВС существенным образом зависят не только от места установки этих датчиков на самолете, но и от режима, полета. С целью выявления характера, влияния параметров набегающего потока на значения локальных газодинамических параметров (числа М/ОС и угла атаки АоА/ОС) в местах расположения датчиков давления и аэродинамических углов предлагается для каждого датчика. СВС создать эмпирико-математическую модель (ЭММ). Напомним, что под ЭММ подразумевается набор аналитических зависимостей, которые в любой точке факторного пространства адекватно отражают функциональную связь между независимыми переменными X — факторами и результатами численного расчета У, — откликами.

^ ^

У = F, (X,b3), где b — вектор коэффициентов, вычисляемый по выборке исходных данных. Для всех рассматриваемых в настоящей главе датчиков в качестве факторов принимаются два параметра набегающего потока: число М^ и угол атаки Ао Аю. Откликами полагаются локальные значения числа М[ос и угла АоА/ос в месте расположения соответствующего датчика. Эмпирико-математическую модель каждого из датчиков, определяющую функциональную связь между значениями локальных газодинамических параметров М[ос, АоА[ос и параметрами набегающего потока М^, Ао А^. предлагается представлять в виде системы линейных по коэффициентам регрессионных уравнений вида

к

ү, = Е b? #чх ), (Ф1)

г =0

где Yj — один из откликов Мі_ос или АоА/_ос, b^ — коэффициенты регрессии, вычисляемые методом наименьших квадратов по результатам параметрического численного эксперимента, f^\x ) определяемые пользователем базисные функции, X — вектор факторов, компонентами которого являются М^нАоА^ . Значения коэффициентов регрессии b^\ определяющих окончательный вид ЭММ (Ф1), вычисляются методом наименьших квадратов с использованием имеющейся выборки исходных данных — дискретного набора результатов численного эксперимента. План параметрических расчетов, т.е количество точек в выборке исходных данных и распределение их в пространстве факторов, существенным образом определяет не только точность определения коэффициентов bp), но и предсказательные свойства всей эмпирико-математической модели.

Выбранный план параметрических расчетов предусматривает две выборки данных: обучающую и контрольную. Распределение в пространстве факторов М^, АоА_ю расчетных точек, соответствующих этим выборкам данных, приводится на рис. 3.

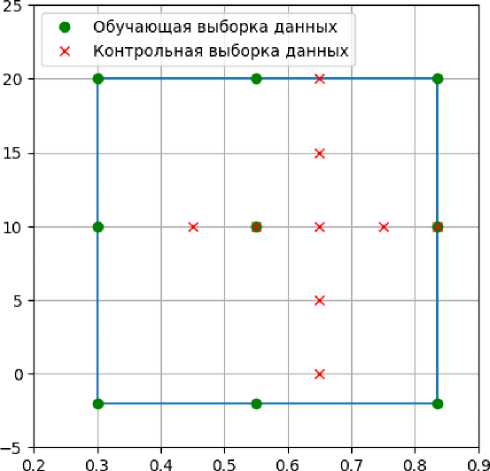
м„

Рис. 3. План численного эксперимента, для датчиков 1, 2

Если обучающая выборка данных предназначена для определения коэффициентов регрессии bp) из (Ф1), то на контрольную выборку данных возлагается двойная нагрузка. На начальном этапе контрольная выборка, данных используется как «затравочный» эксперимент для выявления характера, влияния каждого из факторов на. отклик и выбора, в (Ф1) вида базисных функций //'^(Х). На финальном этапе эта же выборка данных является основой для проверки адекватности полученной ЭММ. Для датчиков 1, 2 объем обеих выборок данных одинаков, но распределение точек в факторном пространстве отличаются. В обучающей выборке даннвіх точки распределены в соответствии с планом полного факторного эксперимента типа 32, а контрольная выборка соответствует плану типа «крест», что позволяет сформировать и проанализировать одномерные сечения Yj(М^) и Yj-(АоА;).

Анализ с помощью системы АРРЕХ [7,8] одномерных сечений Yj (М_;), Yj (АоА_;), соответствующих контрольной выборке данных, показал, что функциональная связь между любым откликом и каждым из факторов Мж,АоА_; адекватно отражается полиномом второй степени. В связи с этим базовый вид многофакторной ЭММ (Ф1) был принят единым для всех откликов каждого из датчиков. Набор базисных функций f ЧЧ^У определяющих вид базовой ЭММ (Ф1), приведен ниже в табл. 4.

Т а б л и ц а 4

Набор базисных функций

І	/Р')(М;,АоА;)	І	/р)(М;,АоА;)
0	1	5	АоА; • МІ
1	М;	6	АоА1
2	2 ∞	7	АоА| • М;
3	АоА;	8	АоА1 • М1
4	АоА; • М;

Сознавая, что для конкретного отклика не все базисные функции из табл. 4 оказывают существенное влияние на отклик, при определении значений коэффициентов b^(j) использовался алгоритм шаговой регрессии [4,5], позволяющий последовательно включать в ЭММ (Ф1) наиболее значимые члены. В результате функциональная связь каждого отклика с факторами М_;, Ао А_; описывалась индивидуальным уравнением регрессии, отличавшимся от остальных не только значением коэффициентов b^(j\ но и набором базисных функций f-^j(М_;, Ао А_;) Ниже для каждого датчика и его откликов М/_осиАо А/_ос приводятся значения коэффициентов регрессии b^(j\ вид базисных функций, включенных в ЭММ, а также величины среднеквадратичного отклонения ss и коэффициента множественной корреляции R, вычисленные по точкам обучающей выборки исходных данных с учетом имеющихся степеней свободы.

Универсальный датчик 1:

ss(АоА/ос) = 9.493713 • 10-2, R(АоА/осy = 9.999929 • 10-1, ss(Мloc) = 6.515050 • 10-4, ^(М/ос) = 9.999979 • 10-1,

М_1ос = -2.861011 • 10^-2 + 1.052812Моо - 2.482684 • 10^-1 М 2 + 1.550818 • 10^-3АоА_ооМ_оо ОС                                                                          X                              OX

+ 9.321476 • 10 4 АоА х М; + 1.992466 • Ю^АоА^М^

АоА/ос = -3.547648 + 4.946775 • 10-1МІ + 1.913333АоА; - 3.535301 • 10^-1 АоА^М^

• -    1.456406 • 10^-2АоА| + 1.316912 • 10^-2АоА| М^

Датчик аэродинамических углов 2:

ss(АоА/осy = 1.336370 • 10-1, Д(АоА/ос) = 9.999772 • 10-1, ss(М/ос) = 1.542206 • 10-3, Д(М/ос) = 9.999868 • 10-1,

М/ос = -2.350614 • 10^-2 + 1.1355262М; - 1.730395 • 10—1МІ + 7.495047 • 10^-3АоА;М;

• -    7.489934 • 10 ³ АоА X М; + 5.389091 • Ю^АоА^М^ + 3.616753 • 10^-4АоА|М|

  АоА/ос = 1.384172 + 5.210050 • 10^-1М; + 2.225950АоА; - 3.420656 • Ю—ЧоА^М^

• -    2.219047 • 10^-2АоА| + 2.475286 • Ю^АоА^М^

Из рассмотрения приведенных выше результатов следует, что для всех созданных ЭММ коэффициент множественной корреляции, характеризующий близость восстановленных данных к исходным, незначительно отличается от 1, а среднеквадратичные ошибки предсказания находятся в допустимых пределах: ss{АоА/_oc} та 0.01, ss{М[_oc} та 0.001. Дополнительное подтверждение адекватности полученных ЭММ иллюстрируется рис. 4 и 5, где приводятся результаты аппроксимации одномерных сечений Yj(М^) и У) (АоА^), соответствующих контрольной выборке данных.

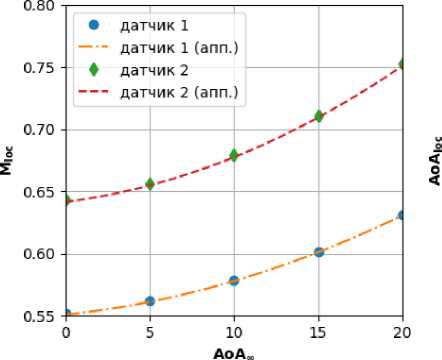
Рис. 4. Аппроксимация зависимостей от АоА _ю

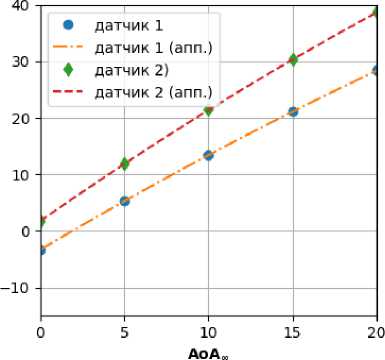
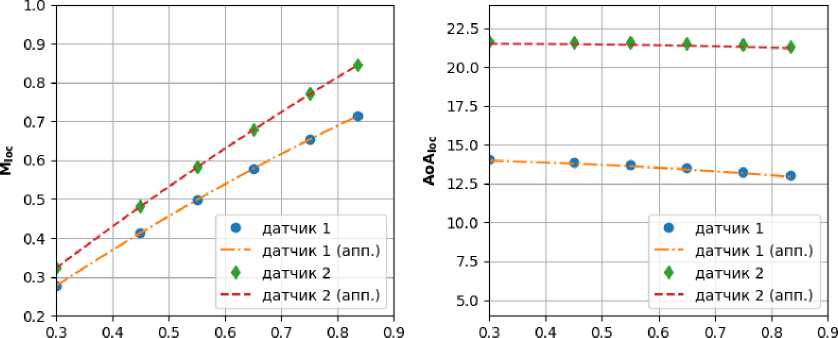
М„                                           М:

Рис. 5. Аппроксимация зависимостей от М ^

Приведенные выше табличные результаты построения ЭММ в сочетании с рис. 4 и 5, иллюстрирующими качество аппроксимации контрольной выборки данных, позволяют характеризовать созданные ЭММ как адекватные и рекомендовать их для использования в решении практических задач. Следует иметь в виду, что область применимости полученных эмпирико-математических моделей ограничена границами области для обучающей выборки данных (на рис. 3 эти границы выделены сплошной линией). Выход за эти границы недопустим, так как предсказательные свойства ЭММ вне области допустимых значений факторов резко ухудшаются.

Расчет полей течения сухого воздуха. Таким образом, функции М[ОС(МЮ, АоА^), АоА[ОС(Мю, АоА^) представлены в виде полиномов второй степени. Для задания режимов полета ЛА, соответствующим локальным параметрам табл. 2, необходимо по результатам предыдущего раздела определить зависимости МЮ(М[ОС, АоА/ОС), АоАго(М[ОС, АоА[Осу Для этого используется функция optimize.root библиотеки scipy [9]. Фрагмент программы на языке python представлен ниже:

def solve (Mfun, AoAfun, M, AoA):

fun = lambda x : [Mfun(x[0] , x[l]) - M, AoAfun(x[0] , x[l]) - AoA] return root(fun, [0.3, 0.0])

sol = solve (Mfun, AoAfun, M, AoA)

print (’ Mach ’, sol.x[0])

print (’ alpha ’, sol.x[l])

В дальнейшем, для каждого датчика по программе [3, 4] проводится серия расчетов полей сухого воздуха (8 расчетов для универсального датчика и 3 расчета для датчика аэродинамических углов, всего 11 расчетов). Точность полученных локальных полей для каждого датчика представлена в табл. 5,6. Наиболее значимые ошибки выделены жирным шрифтом.

Т а б л и ц а 5

Точность локальных полей, универсальный датчик 1

М1ос	АоА1ос	и)	АоАРасчет	МРасчет	АоА?"	М'ошнбка	АоА0шибка
0.3	0	0.337653	1.888843	0.298023	-0.040457	0.002	0.04
0.3	20	3.316532	13.86961	0.299577	19.916355	0.0005	0.09
0.5	0	0.578401	1.904675	0.500332	-0.016213	0.0003	0.02
0.5	10	0.561366	7.781911	0.499543	9.978972	0.0005	0.02
0.5	20	0.534724	14.10025	0.499205	19.929341	0.0008	0.008
0.65	0	0.786656	1.926960	0.653927	0.058331	0.004	0.06
0.65	10	0.757713	8.018121	0.653834	10.013670	0.004	0.02
0.65	20	0.715653	14.38079	0.65342	19.982967	0.003	0.02

Т а б л и ц а б

Точность локальных полей, датчик аэродинамических углов 2

М1ос	АоА1ос	МРасчет	АоАР"	МРасчет	АоА?"	М'ошнбка	АоА0шибка
0.3	0	0.299510	-0.69719	0.299509	0.024045	0.0005	0.03
0.5	0	0.500382	-0.76416	0.498158	0.081794	0.002	0.09
0.65	0	0.660767	-0.82858	0.653666	-0.058860	0.004	0.06

Видно, что максимальная ошибка в моделировании локального числа Маха равна 0.004, а угла атаки - 0.09, что является приемлемым. Рассчитанные локальные поля сухого воздуха могут быть использованы для определения параметров водности в районе датчиков.

3.    Определение параметров поля водности

Результаты расчета относительной водности. Результаты расчетов локальных полей водности представлены ниже в табл. 7, 8. Эти величины задаются при сертификационных испытаниях датчиков.

Для понимания результатов в табл. 7, 8 проанализируем типичное поле водности LWC (рис. 6, 7). В носовой части фюзеляжа происходит накопление воды, далее она начинает растекаться по фюзеляжу вниз по потоку, а затем отрывается от фюзеляжа. Появляется «зона затенения», в которой водность равна нулю. На рис. 6 показано влияние размера капель на режиме М = 0.5, АоА = 0 в сечении Z = 5.0. В верхней части рисунка показано поле водности для капель размером MVD = 20 мкм, снизу - MVD = 1000 мкм.

Таблица?

Относительные значения водности RLWC для универсального датчика 1

м	АоА	MVD (pm)
		20	40	1000	2000
0.3	0°	1.119	1.213	1.014	1.008
	20°	1.108	1.220	-	-
0.5	0°	1.198	1.274	1.018	-
	10°	1.182	1.259	-	-
	20°	1.170	1.265	-	-
0.65	0°	1.286	1.353	1.023	-
	10°	1.254	1.322	1.021	-
	20°	1.226	1.312	-	-

Таблица8

Относительные значения водности RLWC для датчика аэродинамических углов 2

м	АоА	MVD (pm)
		20	40	1000	2000
0.3	0°	1.215	0.0	1.114	1.0554
0.5	0°	0.478	0.0	1.117	-
0.65	0°	0.098	0.0	1.138	-

Видно, что поле течения воздуха оказывает существенно большее влияние на мелкие капли. Крупные капли фактически пробивают зону торможения в носовой части фюзеляжа, «зона затенения» появляется существенно позднее и имеет меньший размер.

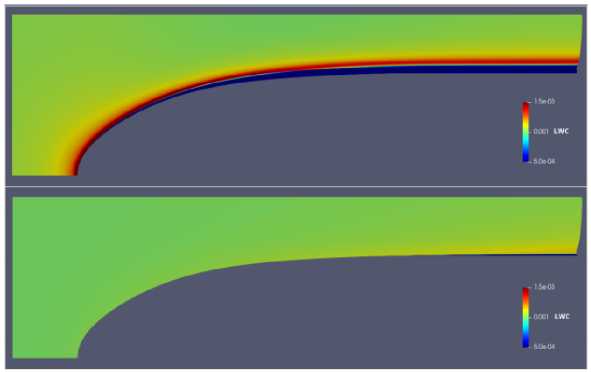
Рис. 6. Влияние размера, капель на обтекание фюзеляжа.

Можно выделить три режима обтекания датчика, которые схематически изображены на. рис. 7:

• 1.    Датчик находится в отрывной зоне. В этом случае коэффициент водности на. датчике равен нулю.

• 2.    Датчик находится в области возмущения водности. Коэффициент водности берется из расчета.

• 3.    Датчик находится в области невозмущенного потока водности. В этом случае коэффициент водности на датчике соответствует таковому в набегающем потоке.

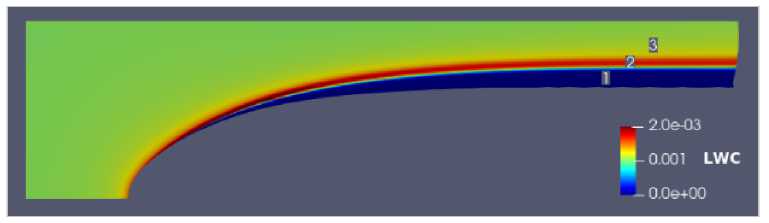
Рис. 7. Три режима, обтекания датчика.

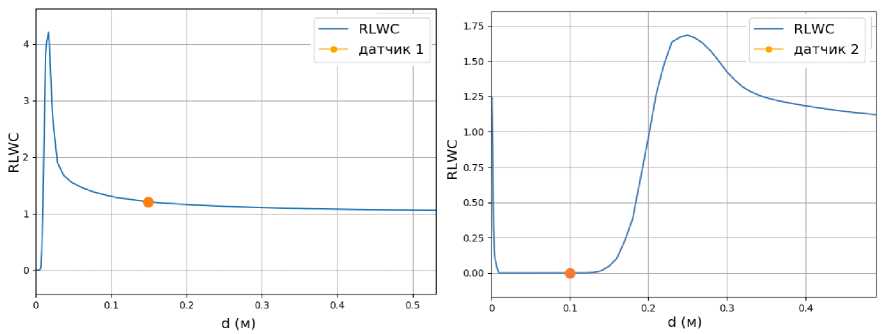
Рис. 8. MVD = 40мкм

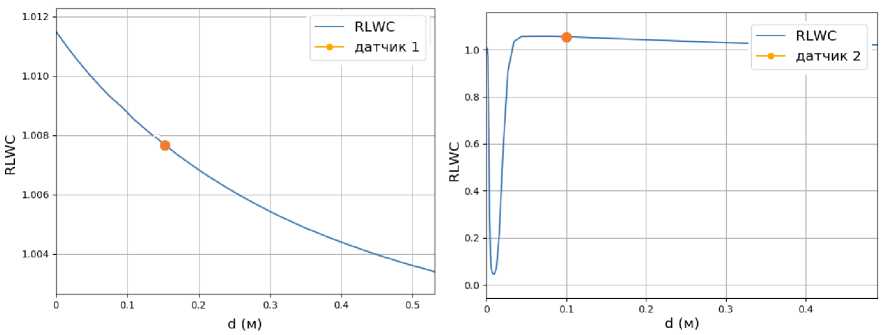
Рис. 9. MVD = 2000 мкм

На рис. 8 и 9 представлены типичные графики распределения относительной водности по нормали к поверхности летательного аппарата.

• 1.    Развитый слой увеличенной водности, отрыв начинается практически с носика. фюзеляжа. Такое распределение водности характерно для капель малых размеров (MVD = 20 — 40 мкм, рис. 8). Для небольших значений продольной координаты, т.е. сечений, где расположены универсальные датчики, датчик попадает в зону 3. При увеличении координаты X, датчик перемещается в зону повышенной водности, а затем в «зону затенения».

• 2.    Слой увеличенной водности тонкий, рост водности незначительный, отрывная зона начинается существенно позднее и имеет небольшие размеры. Такое распределение водности характерно для капель больших размеров (MVD = 1000 — 2000 мкм, рис. 9). В этом случае датчик всегда располагается в зоне 3.

4.    Заключение

Разработана методология определения исходных данных для стендовых испытаний датчиков воздушных сигналов в условиях обледенения. Методология состоит из следующих шагов:

• • Создание эмпирико-математической модели зависимости числа Маха и угла атаки набегающего потока от локальных параметров в районе датчика СВС. Для этого необходимо:

• —    Проведение параметрических расчетов поля воздуха.

• —    Создание эмпирико-математической модели зависимости локальных параметров от параметров набегающего потока.

• —    Решение обратной задачи.

• •    Проведение параметрических расчетов поля воздуха по параметрам набегающего потока, соответствующим локальным параметрам заданных таблицей сертификационного эксперимента.

• •    Проведение параметрических расчетов поля водности по параметрам, заданным таблицей сертификационного эксперимента с целью определения локальных параметров водности в районе датчиков.