Методология построения нелинейной системы управления на основе оптимизации траекторного контура воздушного судна

Управление воздушным судном (ВС) в пространстве условно разделено на два взаимосвязанных уровня - пилотажный и траекторный. Задачей пилотажного уровня является выдерживание углового положения ВС путем изменения моментов управления, задачей траекторного уровня является управление положением центра масс ВС через изменение действующих на ВС сил. Разделение на траекторный и пилотажный контуры основано на различии решаемых задач в этих контурах управления. Однако в процессе реального полета эти задачи взаимосвязаны. Следовательно, управление на пилотажном уровне влечет за собой управление и на траекторном уровне, и наоборот. Ранее, в статье [1] рассматривался вопрос синтеза управления на пилотажном уровне методом ОЗД с последующим решением задач траекторного уровня на основе метода прямого решения задач динамики по результатам пилотажных параметров. Рассмотрим вариант синтеза управления на траекторном уровне методом обратных задач динамики (ОЗД) с последующим решением прямых задач на пилотажном уровне.

• 1.    РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ ДИНАМИКИ ДЛЯ ТРАЕКТОРНОГО КОНТУРА

Траекторное движение ВС определяется значениями линейных ускорений центра масс ВС в траекторной системе координат. Ускорения ВС линейно связанны с перегрузками, измерение которых не вызывает затруднений. Изменение скорости движения центра масс ВС относительно Земли V_K определяется выражением [2,3]:

V K =^ V K + gn - g ^£ 2 ,       (1.1).

где V K - вектор земной скорости ВС, Q — кососимметрическая матрица угловых скоростей специального вида, n - вектор перегрузок, £ 2 – второй столбец матрицы направляющих косинусов скоростной СК относительно нормальной СК. Выполнив обозначение входного воздействия через разность текущей перегрузки и составляющей силы веса, получим выражение векторного уравнения ускорений ВС: *

^V k =^{Q V} k + gn ,        (1.2)

*

где n = n — £ 2 . В скалярном виде выражение (1.2) имеет вид:

• V kx		0	to z	—to y	" V x "		* nx
■ V ky	=	- to z	0	to x	V y	+ g	n y	. (1.3)
■ V kz i		_ to y	—® x	0 .	Vkz _		. n z .

Рассмотрим состояние объекта на интервале времени A t е T, T = [ t ₀, t k ] , в течение которого to s = const, s = x, y, z , t₀ = 0, t k - нефиксированный момент времени.

В начальный момент времени t = 10 = 0 состояния объекта (1.1) характеризуются зна- чениями линейных скоростей VkS (0) = VkS0 и требуется найти такие управляющие воздействия Si (i=э, н, в,), при которых (1.1) переходит из состояния VkS (0) в новое состояние VS и находится в этом состоянии бесконечно долго. В общем случае изменение составляющих скорости по времени VkS = V^S (t), определяют требуемый профиль полёта (пространственную траекторию движения ВС). Оптимальное управление ВС предполагает, чтобы линейные скорости управляемого движения по каждой степени свободы с требуемой точностью следовали за скоростями, определяемыми эталонной моделью

V* _{+ 7} V* + у Г* - / К⁰

V kS ⁺ Z s VkS ⁺ X S 0 V kS A S0^VkS ,     ^(1.4)

С 1 a = c^a, M ) + it 2 a + c f ^e (a f + c f (a f ;

c _{2 a} = c ₂₀ (a, M ) + c ^f (a f_e + c ₂ (a )p +

+ c f (a f + c f"* (a )З_тщ + c f (a )3_np ;       , (1.8)

c з „ = c f ( a , PX +

+ c P ( a , P ) P + c f ( a )5₃

Законы управления перегрузок n^V k ) по каждой степени свободы получаем, используя метод простого градиента

dn S (V_K ) dt

з v Z rSj j=1

S G ( n *)

S n j

, r_Sj = const . (1.9)

где X _S 1 , X _{S 0} - коэффициенты эталонной модели, V kS ( t) ^ V kS при t ^ ”

Численные значения коэффициентов эталонной модели получают идентификацией аэродинамических объектов методом синхронного детектирования [7] на основе пробных воздействий рулей на модель ВС.

Степень приближения управляемого процесса к эталонному движению VS (t) ^ VkS определяется квадратичным функционалом i з

G ( n ') = т E V » - V kS ( t , n ^-(O² , (1.5)

2 1

Согласно (1.9) равны

(1.3), (1.5) компоненты градиента

S G ( n^j)

S n *j

• *        •

= g (V kj - V j) .

(1.10)

который характеризует энергию ускорения поступательного движения в окрестности фазовых траекторий эталонных моделей [6].

При выборе в качестве управляющих функций не отклонения рулей Si ВС, а управляющие силы FS и эквивалентные им перегрузки n*(n = F) , задача синтеза системы управле-G ния может быть решена поэтапно.

На первом этапе синтезируются управляющие воздействия по перегрузке n_S(V_k ) , на втором этапе на основе силовых характеристик ВС [6 -8], определяются законы управления рулями S i , i = в , Э , И :

Подставив (1.10) в (1.9) и проинтегрировав полученное выражение, получим значения потребных значений перегрузки по осям траекторной СК:

з nS (Vk ) = Z rSj (VkS - VkS ) ,      (1.11)

j = 1

где r_S j = gr_S j , требуемые значения V kS вычисляются из эталонной модели (1.4).

Структура матрицы R=||r_sj|| определяется характером перекрёстных связей по управляющим воздействиям в (1.8) и имеет вид)

r11

R = r 21

r12

r32

c f ( a ) c f ( a )

c f ( a )    0

0      c f ^Э ( a )

0 c f ^И ( a , P )

(1.12)

Управляющие воздействия 5 i определяются из уравнений (1.6), (1.7) и (1.8). С одной стороны, из уравнений (1.7) вычисляем коэффици-

енты аэродинамических сил

P *.

---+ П 1 + * ^ 21

n _x

n

n _z

P n —

4 G

n

* n _x

*

n

* n _z

qS

G св

^ 22

23 _

C1 a

Ci

2 a

_ ^c3 a _

,

,

(1.6)

(1.7)

где

mg ( d c ) - 1

ce 7

qS

Dc ce

c 1 a

n^j + ^ 22

n ^j + ⁸ ₂₃

c 2 a , (1.13)

Ci

3 a J

cos a cos P - sin a cos P sin P sin a cos a 0

- cos a sin P   sin a sin P   cos P

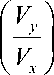
, P = arcsin

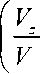
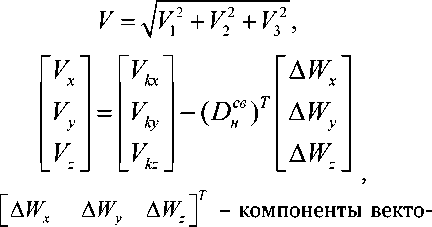
ра скорости, вычисленные в нормальной СК, cosф cos9 sin/ sin ф - cos / cosфsin9 cos/sinф+sin/ cosфsin9

sin 9 cos / cos 9                -sin / cos 9

-sin ф cos 9 sin / cos ф +cos / sin ф sin 9 cos / cos ф - sin / sin ф sin 9

m ₃ - m ₃₀ ( а ) + m ^ ( а ) а + m ^ ³ ( а ) ™ ₃ +

+ m § ( а ) § _в + m f ( а ) ф , го ,

^Ьа ® 3 .

V ’

а - - arctg( Vp), Р - arcsin( Vp),

V - 7 V '² + V 2² + V 2

Вращательное движение ВС описывается динамическими уравнениями Эйлера

е - D C =

направляющие косинусы скоростной СК относительно нормальной СК.

В уравнениях (1.8), неизвестными являются отклонения рулей 5 i , которые определяются через вычисленные (1.13) значения коэффициен-

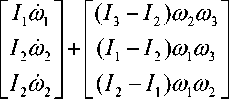
m 1 ( to ) + M 1 m 2^{( to ) + M} 2 m ₃ ( to ) + M ₃

(2.2)

тов аэродинамических сил:

§ ₈ -

с ₂ „ - с _ю( а , М ) - с ф ( аф - с ' ( а ) § - ср * ( а ) § „* - ср ( а§ „ с ? ( а )

5 , -

с , _е - с ₁₀ ( а , М ) - Ас 2 _е - с ? ( а)5_в

с ? ( а )

(1.14)

8 » -

с 3 а - с ^р ( а , Р ) Р - с § ( а ) § с ? ( а , Р )

где m'(rn) - 0, m2(®) - -c2to2 -Kдвю3, m3(™) --c3™3 + Kдвю2 , ms(в) - моменты, характеризующие изменение кинетической энергии вращающихся частей АД и влияние диссипативных сил (s=1..3).

Прямая задача динамики формулируется следующим образом.

Известна математическая модель вращательного движения ВС (2.2) и её состояние в начальный момент времени

tos (0) = tos 0, d)S (0) = to)S 0,5 = 1.3.

Синтезированные ЗУ (1.14) формируются как функции, зависящие от перегрузок, то есть ⁵ в ^{- 5} в ⁽ n y Х ^ э ^- § ₃ ⁽ n x ^, n y Х § „ ^{- 5} н ⁽ n y ^, n z ⁾

или, другими словами, как зависимости от управляющих сил F i ( г = x , y , z ) .

2. РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ ДИНАМИКИ ДЛЯ ПИЛОТАЖНОГО КОНТУРА

(2.3)

Заданы управляющие моменты М _s как функции от го _s . Требуется найти угловые скорости ™ _s - ™ ₅ ( t ), t ^е [ 1 0 , t k ]•

Решение сформулированной задачи сводится к интегрированию замкнутой регулятором (2.1) системы (2.2) с начальными условиями (2.3).

На основе полученного решения в _s= в _s(t)

аналитически или численно интегрируются

Прямая задача динамики предполагает на основе синтезированных законов управления (1.14) определить управляющие аэродинамические моменты M i (i=1,2,3 ^ x,y,z),как функции от угловых скоростей:

M i = qSlm₁, M ₂ = qSlm 2 , M ₃ = qSb a m ₃

M , - M ₁ ( o _l , ro₂\ M ₂ -           (2.1)

- M₂( ro_vto ₂),M ₃ - M₃( to₃)

уравнения Пуассона

^Е '1

^Е 12 . ^Е 13

^Е 21

^Е 22

^Е 23

^S 31 ■

^S 32

Е зз

- ™ з

™ 2

™ 3

- 601

- 6 ^ 2

^Е 11

Ю 1

^Е 12 . ^Е 13

Е 21

Е 22

Е 23

(2.4)

с начальными условиями б ij (0 ), определяемых балансировочными значениями углов Эйлера: 9 (0) - 9_ГП , / (0), ^ (0)^

Для определения текущих углов Эйлера достаточно использовать 3 элемента матрицы на-

где m, - m™ (а)™ + m2 (а)o2 + mp(а)Р +

+ m?(а)§, + m?(а§, ™ - l™2;

m ₂ - m ^ ¹ ( а ) Ю ' + m ^² ( а ) ™ ₂ + m ^p ( а ) Р + + m ₂ ( а ) § _к + m § ( а ) § ₃ , ™ ₂ - ^™™;^

правляющих косинусов:

( ^ 1              ( ^ i

<9 = arcsin s ₁ , у = arccos l — ²— 1 ; ^ = arccos l — ¹— I .(2.5) I cos 9 )            I cos 9 )

Характерным свойством плоско-симметричного ВС является зеркальность геометрических преобразований и преобразований энергии движения.

С учётом сказанного на основе формул, приведенных выше, а также математических

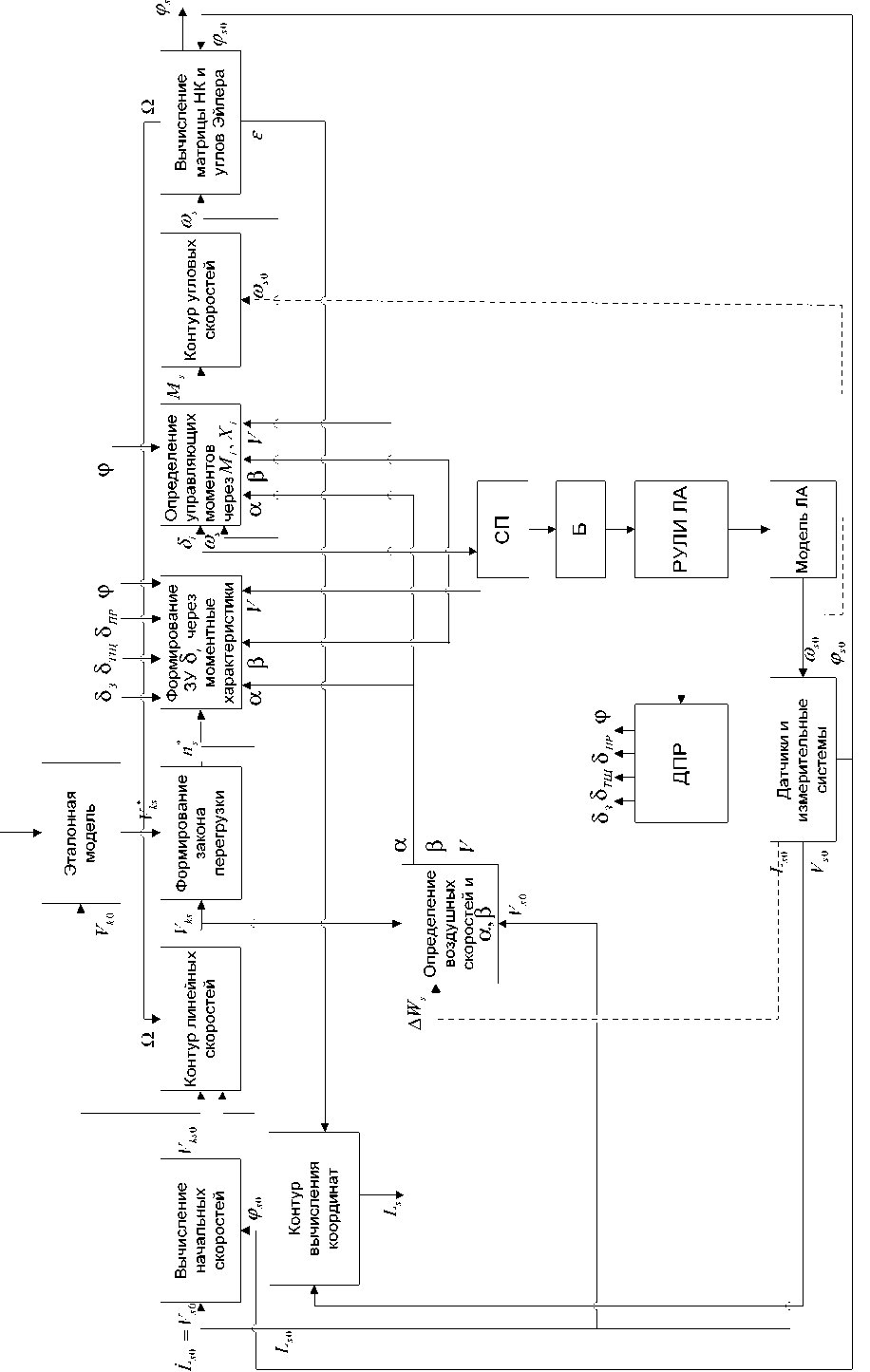
Рис. 1. Функциональная схема траекторного контура управления ВС, построенного через оптимизацию линейных скоростей методом ОЗД зависимостей, определяющих оптимизацию траекторного контура, может быть построена функциональная схема, определяющая архитектурный облик перспективной нелинейной САУ самолётов (рис. 1).

В сравнении с контуром управления через оптимизацию вращательного движения методом ОЗД, приведенного в [1], данный контур построен по методу ОЗД через оптимизацию линейных скоростей. Очевидно, что при их построении нужно учитывать специфику решаемых задач пилотирования. В таких режимах полёта как выполнение различных виражей, а также в режимах стабилизации горизонтального полёта, приведения к горизонту и др. целесообразно оптимизировать контур угловых скоростей. В режимах траекторного управления (полёт по маршруту, маловысотный полет летательного аппарата (ЛА), управление скоростью наноспутников и др.) необходимо использовать оптимизацию контура линейных скоростей.

Таким образом, применение концепций обратных задач динамики в сочетании с организацией контуров управления по принципу симметрии (содержание обратной и прямой задачи динамики обратимо относительно синтезируемых управлений по силовым и моментным ха-

рактеристикам) позволяет научно обосновано решить важную техническую проблему построения нелинейных САУ ВС.