Методология разработки и исследования математических моделей в системах диагностики и функционального анализа ортопедических конструкций на дентальных имплантатах

Результаты анализа и исследований биомеханических процессов в мягких и костных тканях зубочелюстной системы, определяющих надежность её функционирования, показали их прямую зависимость от величин внутренних напряжений и деформаций, возникающих при длительном воздействии рабочих нагрузок [7]. Характер изменений в тканях периодонта после установки имплантатов, связанный с образованием плотной соединительной ткани,

механизмы амортизации давления при нагрузке на имплантаты, включая окружающие их минерализованные ткани, зависит от величин допустимых значений напряжений и деформаций. Замещение части периодонтальной ткани фиброзной изменяет механические и биомеханические свойства системы имплантат-пе-риодонт-челюсть, что связано с риском осложнений, обусловленных перегрузкой опорных тканей.

Современный уровень построения и анализа ортопедических конструкций требует решения большого числа методологических вопросов дентальной имплантологии на основе накопленного практического опыта и теоретических знаний [1]. Однако области концептуальных теоретических знаний и прикладных методик методологически наиболее эффективно могут развиваться и применяться на базе систематизированных информационных систем, обеспечивающих возможность применения вычислительной техники. Особенно это относится к решению множества сложных задач функционального анализа, выбора, обоснования и оценки вариантов лечения, исследования диагностических моделей и др.

Анализ существующих ортопедических конструкций показывает, что величина и направление функциональных нагрузок в них как в биомеханических системах с различными зубочелюстными схемами обуславливают существенное различие в величине сил, действующих на имплантаты, и, соответственно, на кость и прилегающие ткани в зоне контакта с ними [5]. Исследование трёхмерных математических моделей указанных систем показывает, что изменение направления нагрузок в них приводит к существенному перераспределению растягивающих, сжимающих и поперечно-сдвигающих сил, воздействующих на имплантат [8]. В свою очередь, прилегающая к имплантату костная ткань наиболее устойчива в прогнозируемом периоде к сжимающим силам, на 32% менее устойчива к растягивающим и на 68% к силам поперечного сдвига [7], а изменение угла наклона имплантата по отношению к вектору воздействующих на него сил приводит к значительному росту напряжений в зоне контакта кость – имплантат [2]. Отдаленные исследования в костных тканях, подвергающихся длительным нагрузкам выше допустимых, показали их прямую зависимость от величин контактных напряжений [1], что вызывает необходимость детального изучения отдельных фрагментов биомеханических систем или всей системы в целом с объективным учетом воздействия на биологические ткани активных сил и возникающих под их воздействием различных по величине и направлению внутренних напряжений.

Решение задач и использование новых подходов и методов математического моделирования биомеханических систем, расширения информационной базы исследований связано с построением методик диагностики, прогнозирования и оценки различных состояний пациента в долговременном периоде. Одним из определяющих факторов является степень взаимосвязи величин действующих внешних нагрузок на систему и адекватными им напряжениями во взаимодействующих структурнофункциональных элементах биомеханических систем. Многообразие характера и степени взаимосвязей обусловлено видом применяемых материалов, механикой работы систем, особенностями конструкции биомеханических систем, индивидуальными особенностями биохимических и анатомических показателей пациента. Наблюдения в ближайшие сроки надёжности функционирования систем не позволяют провести объективную диагностику и прогнозирование на будущий период с получением ин- формации о факторах, значительно влияющих на исход лечения. В настоящее время достаточно полно изучено анатомо-топографическое строение зубочелюстной системы [3], включая функциональные характеристики, но не решена проблема построения комплексной многокомпонентной математической модели на основе единого формализованного описания однозначной зависимости между варьируемыми параметрами конструкции и технологии установки имплантатов и последующим формированием конструкций съемного или несъемного протезирования.

Цель работы - дальнейшее развитие методологии информационной базы CAD – CAM технологий для виртуального моделирования ортопедических конструкций, расширение возможностей диагностики их состояний [3]. Характер действия нагрузок на компоненты зубочелюстной системы является неоднозначным, зависит от индивидуальных особенностей пациента и других факторов. Методология компьютерного моделирования реальной модели биомеханической системы варьируется в зависимости от анатомо-физиологических условий её функционирования.

Установлено, что неблагоприятный характер фиксации положения центральной окклюзии может привести к дисфункциональным изменениям в височно-нижнечелюстном суставе с локализацией патологических процессов в суставном диске в связи с неблагоприятным распределением в нем напряжений от функциональных нагрузок. Сложность постановки и решения задач исследования влияния нагрузок на состояние тканей и биохимических процессов в них состоит в том, что если модель и содержит полный зубной ряд с соответствующей элементной базой в виде зубных альвеол, периодонтальных щелей, кортикального и губчатого слоев кости, то задание граничных условий для модели осложняется однозначностью механики нижней челюсти только для конкретного строения биомеханической системы. Кроме того, имеются чисто субъективные факторы, оказывающие влияние на схему взаимодействия активных сил, поднимающих нижнюю челюсть [3]. Они определяются строением и расположением жевательных мышц, условиями распределения нагрузки на зубные ряды, реактивными силами, возникающими на поверхности суставной головки мыщелкового отростка. При таких условиях может создаваться дисбаланс сил, поднимающих нижнюю челюсть, и сил с направлением действия со стороны зубных рядов. В зависимости от соотношения величин и направлений действия таких сил могут возникать и локализоваться большие изгибающие напряжения различного знака в неблагоприятных сочетаниях с напряжениями сдвига в различных зонах системы. Особое значение для исследований в этом случае имеет характер и величина изгибных напряжений и величин напряжений от перерезывающих сил на контактируемых поверхностях [4].

Следующими исходными и граничными условиями в разработке математической модели биомеханической системы должны быть механические свойства губчатого и кортикального составов кости, их пористость, характер изменений в тканях периодонта после установки имплантатов, связанных с образованием плотной соединительной ткани, механизмы амортизации давления при нагрузке на имплантаты, включая окружающие их минерализованные ткани [6]. Замещение части периодонтальной ткани фиброзной изменяет механические и биомеханические свойства системы имплантат-пе-риодонт-челюсть, что связано с риском осложнений, обусловленных перегрузкой опорных тканей. Исследования в указанном направлении имеют большое теоретическое и практическое значение, направлены на разработку методов определения значений и схем перераспределения напряжений в сторону физиологически допустимых для тканей, так как в первую очередь это создает нормальные условия для работы и височно-нижнечелюстного сустава, предотвращая возникновение и развитие патологических очагов в том числе и в суставном диске [5].

Построение расчетной схемы биомеханической системы в работе выполнено с учетом работы суставного диска, когда он испытывает неравномерные и достаточно большие нагрузки не только в положении центральной окклюзии, но и в передней, боковой. Такая ситуация создает сложности при математическом описании задачи, а её формализованное представление потребовало введения допущения о том, что модуль упругости материала кости постоянен по её сечению и длине. Также предполагается, что в нижней части внешнего контура кортикальной кости не имеется каких-либо смещений, а на границах смежных подобластей отсутствуют относительные сдвиги материала. Возможное увеличение пористости при соответствующем уменьшении плотности губчатой

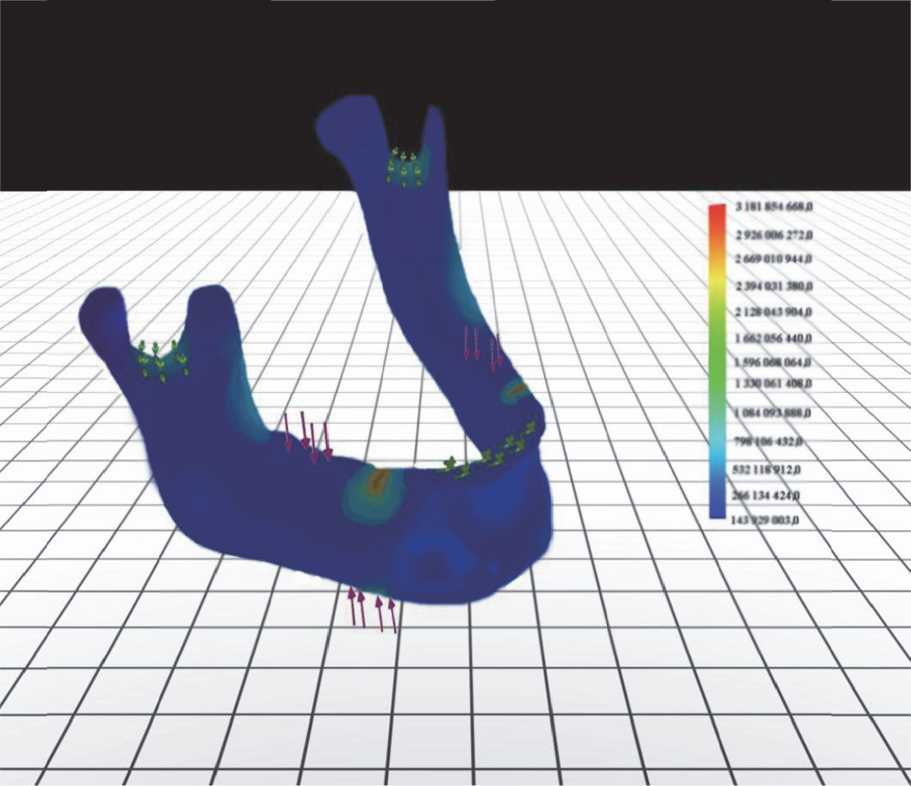
Рис. 1. Математическая модель исследуемой конструкции биомеханической системы – силовая схема нагружения, условия работы, результаты расчета, (схема chelust – нагрузка – напряжение - деформация)

Таблица 1. Исходные и граничные условия для построения математической модели биомеханической системы

Описание

Подвести итог анализа FEM на chelust

Допущения

Информация о модели

Имя документа	Конфигурация	Путь документа	Дата изменения
chelust Свойства исследования Имя исследования	По умолчанию	C:\chelust .sldprt chelust	Fri Jun 18 23:23:07 2017
Тип анализа		Static
Тип сетки: Влияние нагрузок на собственные частоты:		Сетка на твердом теле Выкл
Тепловой эффект:		Исходная температура
Температура при нулевом напряжении		291.000000
Единицы измерения		Kelvin
Включают эффекты давления жидкости из Solid Works Flow Simulation		Выкл
Трение:		Выкл
Игнорировать зазор для поверхностного контакта		Выкл
Использовать адаптивный метод:		Выкл

Единицы измерения

Система единиц измерения:	СИ
Длина/Перемещение	mm
Температура	Kelvin
Давление/Напряжение	N/m2

Свойства материала

No.              Имя тела        Материал        Масса	| Объем
1                   Твердое тело 1      Кость              0,715 kg	0.68 sm3

Имя материала:		Кость
Описание:		-
Источник материала:		Кортикальная и губчатая костная структуры
Тип модели материала:		Линейный Упругий Изотропный
Критерий прочности по умолчанию:		Среднестатистический для конструкции
Данные приложения:		Переменное по длине сечение.
Имя свойства	Значение	Единицы измерения	Тип значения
Модуль упругости	8e+009	N/m2	Постоянный
Коэффициент Пуассона	0.3	NA	Постоянный
Модуль сдвига Предел прочности при растяжении	3.189e+008 3.5e+007	N/m2 N/m2	Постоянный Постоянный
Предел прочности при сжатии	3.5e+007	N/m2	Постоянный
Предел текучести	3.1e+007	N/m2	Постоянный
Теплопроводность	0.2256	W/(m.K)	Постоянный
Удельная теплоемкость	1386	J/(kg.K)	Постоянный

Ограничения и нагрузки:

Крепление

Имя ограничения	Выбранный набор	Описание
Зафиксированный    шарнир-3	Вкл. 2 Грани - Шарнир	Нагрузка     несимметричная, вертикальная односторонняя.
Зафиксированный шарнир -4	Вкл. 1 Грани в зафиксированном состоянии.	Количество степеней свободы -1

Нагрузка

Имя нагрузки Сила-1	Выбранный набор вкл      1      Грани приложение нормальной     силы 6.86e+005 N используя равномерное распределение	Тип нагрузки Последовательное нагружение	Описание Нагрузка симметричная вертикальная.
Сила-2          условно>	вкл 2 Грани применить сила -4.41e+005 N перпендикулярно справочной плоскости относительно выбранной исходной точки,       используя равномерное распределение	Последовательное нагружение	Нагрузка несимметричная,     , дополнительная боковая сила.

Контакт:

Состояние контакта: Соприкасающиеся грани - Свободные

Тип конструкции - рама

Характер нагружения - статический   Данные отсутствуют.

Результаты исследования - обобщены по диапазонам нагрузок.

Имя	Тип	Мин	Макс
Напряжение	VON: Напряжение Von Mises	143929 N/m^2 Узел: 13557 1-йвариант 2-й вариант 3-й вариант	3.19199e+009 N/mA2   Узел: 538 1-й вариант 2-й вариант 3-й вариант

Выбранный набор Единицы измерения Сумма по X Сумма по Y Сумма по Z Результирующая Все тело        N              -2.92542       490003         -3.03857 Силы реакции: 1. Силовые факторы нагружаемого свободного тела 490003 Выбранный набор Единицы измерения Сумма по X Сумма по Y Сумма по Z Результирующая Все тело N 0.0262399 -0.373849 0.233741 0.441686 о о

о

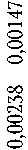
S г

2. Моменты свободного тела

деформация     Элемент: mm,                     2219          0.825049

7948      -60.4339                                 mm, mm,                                     -86.2672

-166.172                                 mm)

mm)

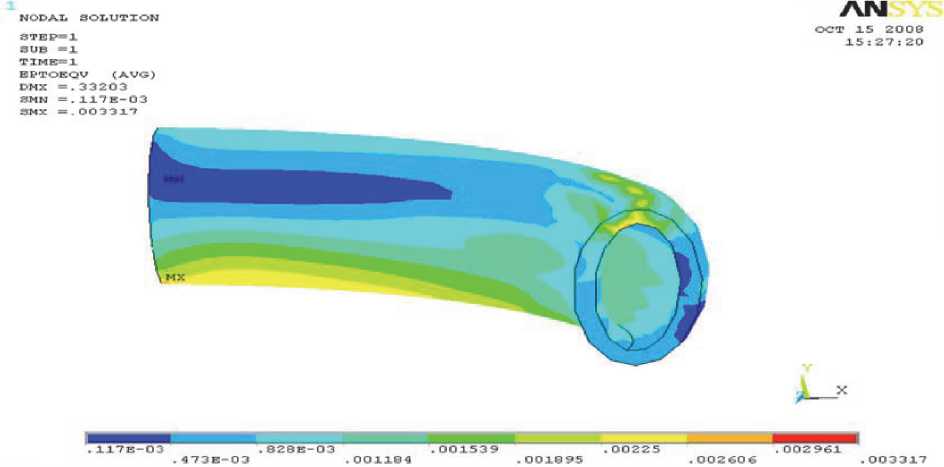
Рис. 2. Один из результатов вариантов исследований параметров системы по схеме 1 – поле эквивалентных напряжений по Мизесу в зоне установки имплантата в губчатой кости при рабочей нагрузке 35кГ

кости учитывается по среднестатистическим показателям. Модель исследуемой биомеханической конструкции с расчетной схемой нагрузок представлена на рис. 1. Исходные и граничные условия представлены в таблице 1. Условия построения расчетной схемы представлены в соответствии с рекомендуемой методикой согласно требованиям по стандартам. Результаты расчетов представлены в таблицах и графиках.

Для вариантов с различными значениями рабочих нагрузок в биомеханической системе по выбранной схеме её функционирования ниже представлены полученные расчётные значения значимых силовых факторов. Для детального анализа характеристик системы при воздействии нагрузок могут быть рассмотрены её отдельные структурно-функциональные составляющие по тестовым значениям величин рабочих нагрузок и по характерным схемам нагружения.

Схема 1 (схема 1-sym) - симметричная и несимметричная нагрузка. Усилие в мышце 35 кг.

Результат – рабочая нагрузка, развиваемая на имплантанте №6 (симметрично) составляет Qy = 21,1 кг. В шарнирной сумке вертикальная реакция Fy=16,7 кг, боковая реакция Fx=0,2 кг (-0,2 кг) в левом (правом) соответственно. Установлено, что зона локализации максимальных значений сжимающих напряжений в кости в данном варианте исследования схемы находится в месте опоры ортопедической конструкции на имплантат (Рис. 2).

Случай B – несимметричное нагружение (схема 2-й вариант), рабочая нагрузка только слева. Усилие в мышце 35 кг. Результат – рабочая нагрузка, развиваемая на имплантанте №6 (только слева) составляет Qy = 19,2 кг.

В шарнирной сумке: - со стороны воздействия рабочей нагрузки вертикальная левая реакция Fy = 5,3 кг, боковая реакция Fx= 0,4 кг; с другой стороны вертикальная правая реакция Fy = 9,4 кг, боковая реакция Fx= – 0,4 кг.

Случай C – несимметричное нагружение (схема 3-й вариант): рабочая нагрузка (нагрузка вертикальная слева + боковая сила слева) - усилие в мышце 35 кг.

Результат –рабочая нагрузка, развиваемая на имплантанте №6 (только слева) Qc = 19,2 кг, боковая сила 5,5 кг. В шарнирной сумке:

• -    со стороны воздействия рабочей нагрузки вертикальная левая реакция Fy = 2,5 кг, боковая реакция Fx= 3,3 кг, продольная реакция Fz=-6,5 кг

• -    с другой стороны вертикальная правая реакция Fy = 21,3 кг, боковая реакция Fx=–2,2 кг, продольная реакция Fz=6,5 кг.

• -    с другой стороны вертикальная правая реакция Fy = 21,3 кг, боковая реакция Fx=–2,2 кг, продольная реакция Fz=6,5 кг

Аналогичные расчеты по предлагаемой схеме и по условиям исследований модели выполняются для каждого варианта анализируемого множества проектов и рабочих состояний.

Значения полученных напряжений и деформаций в последующих исследованиях определяют характер поведения биомеханической системы челюсть- протез-имплантат по системным факторам, определяющим состоятельность и надежность биомеханической системы и ортопедической конструкции в отдалённые периоды.

ЗАКЛЮЧЕНИЕ

Применение методик объективных исследований на базе CAD/CAM технологий, включающих стандартизованные проектные и расчетные модули в сочетании с применением в последующем биомеханических методов исследований, позволяет оптимизировать решение задач с разделением работы на точные технологические этапы.

Моделирование систем позволяет на более высоком уровне обеспечивать логическую увязку способов повышения качества конструирования протезов различной сложности, определять необходимые параметры титановых имплантатов и схем их установки. построение соответствующего программного обеспечения, позволяющего обеспечивать максимальную точность воспроизведения исполнительных размеров для установки имплантатов, изготовления ортопедических конструкций по индивидуальным данным с использованием оборудования с числовым программным управлением.

Исследования показали, что сложность построения математической модели структурнофункциональной системы заключается и в том, что учитываемые индивидуальные особенности на начальных этапах проектов могут изменять свои параметры с течением времени. Это объясняется тем. что в каждом случае после установки имплантатов и протезов проявляются относительно новые взаимоотношения между существовавшими ранее физиологическими последовательностями движений нижней челюсти, строго регламентированными нервными импульсами, поступающими с рецепторных полей различных участков зубочелюстной системы, и новыми, появившимся в связи с перераспределением напряженно-деформированного состояния основных тканей.

Полученные результаты позволяют расширять теоретическую базу для проведения дальнейших исследований в области изучения взаимосвязи характера и величин напряжений в биомеханической системе с состоянием тканей и прогнозирования их поведения и свойств в долговременном периоде.