Методология системного анализа взаимосвязей между факторами риска и здоровьем населения в задаче устойчивого развития

В рамках современной парадигмы принята триединая концепция устойчивого эколого-социально-экономического развития.

Первая из них - экономическая ( Economic ) составляющая представляет собой общепринятую форму капитала, используемую в экономическом анализе, и включает в себя здания, промышленное оборудование и машины, компоненты инфраструктуры и т.п., т.е. все то, что создано человеком.

Вторая составляющая – социальная ( Social ) - ориентирована на человека и направлена на сохранение стабильности социальных и культурных систем. Это «располагаемый человеком запас знаний, навыков, способностей и других атрибутов». Очевидно, что интеллект, знания не могут быть оторваны от своего носителя – человека. Таким образом, в современных условиях на первое место в стратегии устойчивого развития общества должны выступать целевые установки, связанные с возрастанием «человеческого капитала». В первую очередь речь должна идти об укреплении здоровья населения, увеличении продолжительности активной жизни (как одного из главных индикаторов здоровья), повышении уровня образования, развитии науки, т.е. в целом - повышении качества жизни.

Третья составляющая - окружающая среда (Environment). Оно включает помимо традиционно рассматривающихся природных ресурсов также и созданную человеком городскую среду со всеми присущими городу факторами риска.

Соотношение между аспектами (компонентами) триединой концепции может (и будет) изменяться со временем. Так, доля природных ресурсов с течением времени, скорее всего, начнет уменьшаться. При этом резкое смещение центра тяжести в какую-либо сторону уводит систему в зону неустойчивого развития, при этом возможности замещения компонент из разных составляющих крайне ограничены, если мы хотим оставаться в этой зоне.

В настоящей работе проводится анализ поведения системы, подвергающейся воздействию большого числа факторов различной природы (экономических, социальных, факторов окружающей среды). В качестве примера рассмотрена задача о здоровье населения, подвергающегося воздействию факторов риска различной природы. В общем вопрос ставится следующим образом: как найти наиболее важные факторы, контроль за которыми обеспечивает устойчивое развитие, как снизить негативный эффект факторов риска, которых невозможно избежать [Сорокин, 2009]?

Общая постановка задачи

Пусть имеется набор факторов ФР1, ФР2, ….., оказывающих влияние на отклик W. В нашем классе задач W – доля объектов исследования, обладающих некоторым заданным свойством. Факторы разделяют изучаемые объекты на группы по уровням факторов; например, если фактор ФР1 принимает два значения ФР1=0 и ФР1=1, тогда отклик W принимает два значения W(ФР1=0)=W0 и W(ФР1=1)=W1. При рассмотрении комплекса из нескольких факторов (два фактора и более) изучаемые объекты разделяются на множество подгрупп, определяемых набором уровней всех факторов комплекса, а отклик принимает значения Wijl , где каждый индекс соответствует определенному фактору (количество индексов равно числу факторов в комплексе).

Примером отклика W описанного типа может служить заболеваемость населения (доля лиц, имеющих изучаемое заболевание W=n/N, где n-число лиц с заболеванием среди полного числа N); примерами факторов, оказывающих влияние на отклик (здоровье населения), являются загрязнение окружающей среды (обычно представляется в виде категорий «Сильное», «Умеренное», «Слабое»), курение (курит/не курит), образование (высшее, среднее специальное, среднее) и др.[Константинова, Вараксин, 2007г.].

Задача ставится следующим образом: найти комплекс факторов и конкретные комбинации уровней факторов, таких, чтобы значения отклика W ijl… были экстремальны (максимальны либо минимальны) при максимально возможной численности групп; возможны варианты условий экстремальности. Пример постановки задачи: найти комплекс факторов, оказывающих наибольшее влияние на здоровье населения. Варианты постановки задачи: найти комплекс факторов, оказывающих наибольшее негативное влияние на здоровье; найти факторы, позволяющие компенсировать негативное влияние на здоровье заданного комплекса факторов риска.

Задача о здоровье населения (и аналогичные задачи) обладает определенной спецификой.

• а)    Необходима количественная оценка эффекта комплекса факторов, выполненная для конкретной популяции. Часто встречающиеся в литературе утверждения типа «Загрязнение окружающей среды обуславливает 30% всех заболеваний» без указания популяции, без указания типа и уровней загрязнения – не годятся в принципе. Нужна методология, применимая для конкретных условий; при этом, методология должна допускать применение к любой другой популяции без изменения принципов (работать «в общем случае»).

• b)    Для того, чтобы методология работала «в общем случае» нужен комплексный (системный) подход, так, чтобы ответ был не абсолютно частный (который может измениться при малейшем изменении первичных данных), а устойчивый к возможным (реально допустимым) изменениям условий существования популяции. Нужен подход, который давал бы не просто числа, но позволял бы выдвигать и проверять предметные гипотезы (примеры приведены ниже).

• c)    Кроме требований конкретности и устойчивости, сформулированных выше, построенные модели должны удовлетворять требованиям понятности (интерпретируемости), практической реализуемости и полезности: результаты должны быть понятны специалисту в предметной области (медику-исследователю и медику- практикующему врачу), их можно реализовать на практике с очевидной пользой для пациентов.

Факторы

В предлагаемом подходе факторы являются (с точки зрения математики) категоризированными переменными, имеющими несколько градаций (две-три). Примеры таких факторов для задачи о здоровье населения приведены выше. Существующие подходы к оценке влияния комплекса факторов на отклик W (многофакторный отклик, многофакторный анализ) базируются, чаще всего, на предположении о независимости факторов (фактор ФР1 изменяется независимо от фактора ФР2 и также все остальные), либо на неявном предположении, что взаимосвязь между факторами не оказывает существенного влияния на результат. Основное отличие нашего подхода от имеющихся – явная декларация наличия значимых корреляций между факторами и необходимость учета этих корреляций при определении отклика.

Статистические взаимосвязи между категоризированными факторами с небольшим числом градаций устанавливаются с помощью таблиц сопряженности признаков.

Статистическая значимость связи определяется критерием хи-квадрат, сила связи – мерой

Крамера (или другими аналогичными мерами). После определения связей между всеми

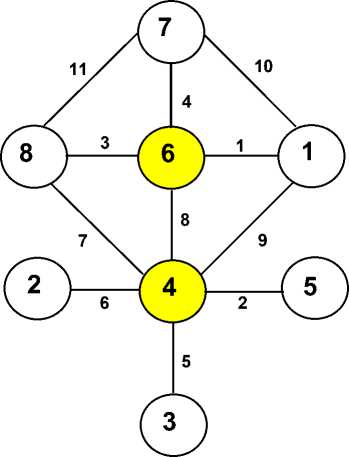
Рис. 1. Граф корреляционной плеяды

парами факторов, необходимо дать наглядное (графическое) представление всех связей в виде, например, графа корреляционных плеяд [Терентьев, 1977г., Миркин, 1985г.].

В качестве примера приведем результаты исследования взаимосвязей между факторами в задаче о здоровье населения. В работе исследованы 441 семья детей-дошкольников Екатеринбурга, посещающие детские дошкольные учреждения. Факторами, которые оказывают возможное влияние на здоровье детей (W – распространенность какой-либо патологии), являются факторы семьи. Графическое представление связей между этими факторами («портрет» семьи в координатах семейных факторов) показано на рис. 1 [Вараксин, Живодеров, 2009г.].

Факторы риска на рис. 1.:

• 1    – тип питьевой воды

• 2    – санитарное состояние квартиры

• 3    – семья полная / неполная

• 4    – материальная обеспеченность семьи

• 5    – психологический климат семьи

• 6    – образование матери

• 7    – курение матери (есть, нет)

• 8    – физическая активность ребенка

На рис. 1. кружками обозначены факторы (цифра в кружке – номер фактора), а линиями – связи между факторами; номера у линий показывают ранг (силу) связи. Самая сильная связь (ранг 1) наблюдается между ФР «образованием матери» и «тип питьевой воды»; как и следовало ожидать, в семьях с более высоким образованием матери чаще употребляют чистую или фильтрованную воду. Проанализировав граф, мы выделили два «системообразующих» (имеющих наибольшее количество связей) фактора: образование матери (фактор № 6) и материальная обеспеченность семьи (№ 4).

Понятие эффекта

При изучении одного, двух и многих факторов возникают, соответственно, одно-, двух- и многофакторные эффекты. Под однофакторным эффектом бинарного фактора ФР, принимающего значения 0 и 1, мы понимаем величину

ΔW1(ФР) = W 1 – W 0 ,                                                       (1)

где W 1 = W(ФР=1), а W 0 = W(ФР=0). В задаче о здоровье населения W 1 и W 0 – это распространенности некоторой патологии при наличии и отсутствии одного фактора риска соответственно. В доказательной медицине величина ΔW1 (1) называется «Добавочный риск – Attributable Risk» [Флетчер, 1998г.].

При наличии двух бинарных факторов ФР1 и ФР2 появляются 4 значения отклика: W 00 , W 01 , W 10 и W 11 с очевидным смыслом.

Двухфакторным эффектом называют величину:

ΔW2 = W 11 – W 00 ,                                                           (2)

где W 11 = W(ФР1=1, ФР2=1);

W 00 = W(ФР1=0, ФР2=0).

В случае двух бинарных факторов возможны 4 однофакторных эффекта, когда эффект одного фактора определяется на фиксированном уровне второго фактора: ΔW1(ФР1,ФР2=0)=W 10 –W 00 , ΔW1(ФР1,ФР2=1)=W 11 –W 01 , ΔW1(ФР2,ФР1=0)=W 01 –W 00 , ΔW1(ФР2, ФР1=1)=W 11 –W 10 . Так, например, разность (W 10 – W 00 ) - это эффект, обусловленный первым фактором ФР1, на фиксированном уровне второго фактора ФР2=0.

Хорошим способом осмысления двухфакторных эффектов является их графическое представление. Пример из области здоровья населения приведен на рис. 2. Рисунок наглядно показывает, что распространенность заболевания увеличивается при действии каждого из факторов риска (газовая плита и недостаточный уровень физической активности ребенка), причем их совместное действие близко к аддитивному (прямые линии практически параллельны).

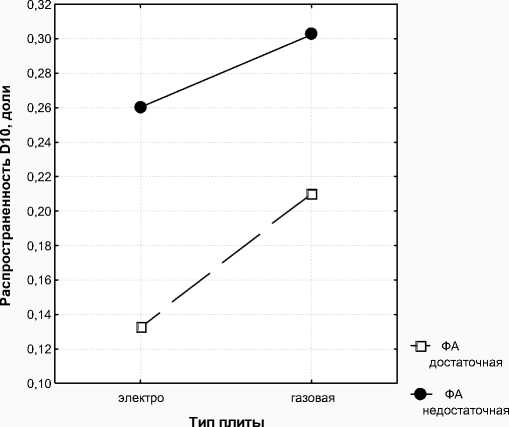
Рис. 2. Распространенность W болезней органов дыхания (класс болезней D10) при совместном действии двух факторов: ФР1-тип плиты в квартире (0-электрическая плита, 1-газовая плита) и ФР2-уровень физической активности ребенка (0-достаточная, 1-недостаточная ФА)

Для науки и практики наиболее интересны так называемые неаддитивные эффекты действия комплекса факторов на отклик W. В случае двух бинарных ФР условие аддитивности выражается соотношением

(W 11 – W 00 ) = (W 10 – W 00 ) + ( W 01 – W 00 ).                                          (3)

Можно показать, что формула (2) является обобщением соотношения классического дисперсионного анализа, которое (в стандартных обозначениях) имеет вид [Юнкеров, 2005г.]

( y ij - y i • - y • j + y ) = 0 .                                                              (4)

Формула (2) получается из (3) в предположении, что аналогом среднего значения Y ij в дисперсионном анализе является распространенность патологии W ij .

Согласно представлениям о комбинированном действии факторов, введенным в токсикологии [Кацнельсон, 2002г.], нарушение равенства (2) описывает эффекты антагонизма (когда левая часть (2) меньше правой), либо синергизма (в обратном случае). В первом случае совместный эффект действия двух факторов оказывается меньше суммы однофакторных эффектов, во втором – больше данной суммы. В задаче о здоровье населения это означает, что знание однофакторных эффектов двух ФР при антагонизме позволяет оценить верхний предел угрозы, которую представляют два фактора риска для здоровья населения, а при синергизме однофакторные эффекты не гарантируют такой оценки и возможны сильные неблагоприятные последствия. Естественно, что выполнение (нарушение) равенства (2) должно рассматриваться не в алгебраическом, а в статистическом смысле, т.е. оценка нарушения (2) должна проводиться с помощью статистических критериев на заданном уровне статистической значимости.

Нарушение равенства (2), кроме проявления эффектов антагонизма и синергизма, может также выражаться в предметно-значимых и понятных специалисту эффектах, таких как:

• •    W 11 из формулы (2) значительно больше любого однофакторного W 1 из формулы (1); это означает, что одновременное действие двух факторов приводит к значительному увеличению W (например, распространенности патологии) по сравнению с действием каждого фактора отдельно;

• •    W 00 значительно ниже любого однофакторного W 0 ; это означает, что одновременное устранение двух факторов приводит к снижению ( резкому снижению) W по сравнению с устранением одного ФР;

• •    W 10 либо W 01 значительно меньше одного из однофакторных W 1 ; это означает, что устранение одного ФР способно компенсировать негативное влияние другого ФР. Влияние коррелированности факторов на отклик

Начнем рассмотрение возможного влияние коррелированности факторов с однофакторного эффекта.

В общем случае проблема формулируется следующим образом. Пусть имеется два фактора ФР1 и ФР2, оказывающих влияние на отклик W. Пусть также между ФР1 и ФР2 имеется статистически значимая взаимосвязь. Для описания этой взаимосвязи используется, как отмечалось выше, метод таблиц сопряженности признаков. Пример таблицы сопряженности приведен ниже.

Таблица 1. Таблица сопряженности признаков ФР1 и ФР2 (таблица наблюдаемых частот n ij )

Фактор	ФР1=0	ФР1=1	ФР1=0 и 1
ФР2=0	n 00	n 10	n . 0
ФР2=1	n 01	n 11	n . 1
ФР2=0 и 1	n 0 .	n 1 .	N

В таблице 1 наблюдаемые частоты n ij – это число объектов исследования, которые одновременно принадлежат уровню ФР1= i и ФР2= j . В последней колонке и последней строке таблицы представлены маргинальные частоты, например, n . 0 равно сумме n 00 и n 10 , а n 0 . равно n 00 + n 01 . Общее число объектов обозначается N. Если бы факторы ФР1 и ФР2 были независимы, тогда частоты n ij (так называемые ожидаемые частоты n * ij ) были бы равны:

nn

.

n * = ^{i . . j} ij _N

Соотношение (4) выражает тот факт, что вероятность попадания объекта в одну из «клеток» табл. 1, находящуюся на пересечении столбца i и строки j , определяется произведением вероятностей попасть в столбец i и строку j (условие независимости событий).

Представим ситуацию, когда частоты n 00 и n 11 оказываются больше соответствующих n* 00 и n* 11 , а частоты n 10 и n 01 – меньше чем n* 10 и n* 01 . Эта ситуация является аналогом положительной корреляционной связи в том случае, если бы ФР1 и ФР2 были бы количественными переменными. Предположим также, что W(ФР1=1)>W(ФР1=0) и W(ФР2=1)>W(ФР2=0), т.е оба фактора при изолированном действии увеличивают значение отклика W. В этой ситуации однофакторный эффект ΔW1(ФР1) = W 1 – W 0 , который должен отражать изменение W при изменении одного фактора ФР1, фактически описывает изменение W при одновременном изменении как ФР1, так и ФР2.

В этой ситуации возникает вопрос: возможно ли определение однофакторного эффекта ФР1 «в чистом виде», без влияния второго фактора ФР2 ? В точной постановке вопроса - ответ отрицательный: невозможно «избавиться» от влияния ФР2 в ситуации, когда ФР2 тесно связан с ФР1. С точки зрения математики отрицательный ответ на поставленный вопрос понятен [Налимов, 1971г.]. Для того, чтобы этот ответ был понятен на уровне «обыденного сознания», проведем аналогию с воздействием на некий отклик W смеси химических реактивов. Итак, пусть имеется смесь химических веществ ФР1 и ФР2, вызывающая некоторую реакцию W. Допустим, в проводимых экспериментах делается попытка установить зависимость типа «Доза-ответ», когда реакция W регистрируется при различных дозах химических веществ. Если увеличение дозы организуется путем увеличения объема смеси при неизменном и жестком соотношении количеств первого и второго вещества, тогда и реакция системы наблюдается при одновременном воздействии ФР1 и ФР2. Очевидно, что результаты такого эксперимента не позволяют определить, как действует на W каждое вещество отдельно от другого.

Если же концентрации веществ ФР1 и ФР2 в смеси коррелируют (изменяются синхронно в статистическом смысле), но отсутствует жесткая связь между количеством ФР1 и ФР2, есть возможность сделать оценку порядка величины изменения однофакторного эффекта ΔW1(ФР1) за счет влияния ФР2. Для этого можно использовать так называемую процедуру «линейной интерполяции» для корректировки однофакторных эффектов при наличии коррелированных факторов, описанную в [Вараксин, Константинова, 2009 г.]. Другой способ корректировки однофакторных эффектов основан на использовании данных двухфакторной таблицы. Пусть имеется два бинарных фактора ФР1 и ФР2, оказывающих влияние на отклик W, причем ФР1 считается основным фактором, влияние которого надо изучить, а ФР2 является фактором, «мешающим» (по терминологии доказательной медицины [Флетчер, 1998г.; Привалова, 2003г.]) изучению влияния ФР1. Задача заключается в том, чтобы попытаться выявить влияние ФР1 на W в более «чистом» виде, устранив мешающее влияние ФР2. Для решения поставленной задачи составляется двухфакторная таблица, представленная ниже.

Таблица 2. Двухфакторная таблица Cell Statistics при одновременном действии на W двух факторов

N	Факторы	Уровни ФР1	Уровни ФР2	Число объектов	W
1	ФР1	0		n 0.	W 0 (ФР1)
2	ФР1	1		n 1.	W 1 (ФР1)
3	ФР2		0	n .0	W 0 (ФР2)
4	ФР2		1	n .1	W 1 (ФР2)
5	ФР1 + ФР2	0	0	n 00	W 00
6	ФР1 + ФР2	0	1	n 01	W 01
7	ФР1 + ФР2	1	0	n 10	W 10
8	ФР1 + ФР2	1	1	n 11	W 11
9	Все объекты вместе			N	W

Надо отметить, что «устранить» влияние ФР2 можно только путем задания конкретных условий такого устранения. В качестве наиболее естественного условия можно предложить следующее: соотношение распространенностей второго фактора ФР2 на уровне ФР1=0 (это числа n ₀₀ и n ₀₁ ) и на уровне ФР1=2 (числа n ₁₀ и n ₁₁ ) должно быть такое же, как для всех объектов вместе на уровнях ФР2 без разделения на уровни ФР1 ( n .₀ и n .₁). Тогда нескорректированный однофакторный эффект фактора ФР1, введенный ранее соотношением (1), выражается как

A W 1(OD1) = W 1 (OD1) - W 0 ( 05 1)

^W 10 n 10 + ^W 11 n il   ^W 00 n 00   W 01 n 01

N

а скорректированный ( adjusted ) на влияние ФР2 как:

A W 1 adj (OB1) =

W 10 n . 0 ⁺ W 11 n . 1 ^- W 00 n . 0 ^- W 01 n . 1

N

Задача выбора факторов и двухфакторных комплексов, оказывающих наибольшее влияние на отклик

Задача выбора факторов (k=1) и двухфакторных (k=2) комплексов выделена в отдельную задачу (отдельную от случая k>2), потому, что она решается точно путем полного перебора всех возможных вариантов. В случае k>2 такой перебор либо слишком трудоемкий, либо принципиально невозможен.

В случае k =1 проводится расчет однофакторных эффектов всех факторов по формуле (1) и отбираются наиболее значимые из них. В техническом плане это простейшая операция, которая с помощью компьютера может быть выполнена для любого исходного числа числа факторов. Например, в задаче о здоровье населения в наших исследованиях первоначальное число факторов равно 150. Число реально значимых факторов, дающих статистически значимые однофакторные эффекты, оказывается гораздо меньше; для разных патологий оно варьируется от 2-3 до 8-10 факторов (гораздо меньше исходных 150).

В случае k =2 даже технически задача оказывается гораздо сложнее. В этом случае для каждой пары факторов из первоначально большого числа факторов необходимо построить таблицу типа табл. 1 и, как минимум, сделать оценку величины и статистической значимости двухфакторного эффекта. Если же выполняется программа-максимум, тогда необходимо рассчитать все 4 однофакторных эффекта, оценить их статистическую значимость и определить тип комбинированного действия данной пары факторов.

Даже при большом числе исходных факторов программу-минимум можно выполнить путем полного перебора всех пар факторов. Это возможно двумя путями. Первый – написать собственную компьютерную программу, рассчитывающую двухфакторные эффекты и уровень их значимости. Второй – использовать существующие статистические компьютерные пакеты программ (например, программу Statistica for Windows) для оценки величины и значимости конкретного парного эффекта и собственную подпрограмму, которая работает в среде статистического пакета, с целью организации перебора всех пар факторов. Результаты расчетов заносятся в базу данных, автоматически упорядочиваются по величине эффекта, что позволяет легко отобрать необходимое для дальнейшего анализа число пар факторов, оказывающих максимальное влияние на отклик W.

Именно такой подход реализован нами. Временные затраты оказываются следующими: если путем первичного анализа однофакторных эффектов сократить исходное число факторов до порядка 30, тогда полный перебор всех возможных пар факторов занимает порядка 2-3 часов счета на стандартном персональном компьютере.

Многофакторные эффекты при k>2

Задача поиска многофакторных комплексов (k>2), оказывающих на отклик W максимальное влияние, не может быть решена путем полного перебора всех вариантов (всех сочетаний k факторов). Отсюда следует невозможность получения одного абсолютно лучшего (с точки зрения заданного критерия) решения. В результате мы попадаем в поле действия широко распространенного принципа множественности моделей [Налимов, 1971г.], согласно которому сложная система может (должна) описываться многими дополняющими друг друга моделями, каждая из которых отражает наиболее полно какую-либо сторону функционирования описываемой системы. Именно такая идеология реализована нами на основе идеи иерархической классификации.

Покажем реализацию данной идеологии на примере задачи о здоровье населения.

Основная задача, которая ставится при изучении многофакторных эффектов – нахождение таких комбинаций факторов и их градаций, которые приводят к резкому повышению (или понижению) распространенности изучаемой патологии W по сравнению с одно- и двухфакторными воздействиями. Какие здесь возникают трудности ?

• •    большое число многофакторных комбинаций;

• •    большое число различных градаций для заданной комбинации факторов и соответствующих им значений W ij распространенности патологии;

• •    для реального (практического) использования полученных многофакторных результатов недостаточно просто перечислить факторы, которые при совместном действии дают максимальный эффект; итогом анализа должна стать формулировка некоего простого и понятного специалисту (медику-исследователю и медику-практику) правила, по которому определяются классы детей с низкой и высокой распространенностью патологии. Построение этого правила (решающего правила по терминологии теории классификации) в принципе не может быть алгоритмизировано и является результатом экспертной работы специалиста по анализу данных. Само правило служит для специалиста-медика основой для разработки мероприятий по снижению заболеваемости детей.

Итак, с увеличением числа ФР число различных комбинаций факторов и количество W ij для каждой комбинации факторов увеличивается, в результате чего их экспертный анализ становится непростой задачей; поэтому требуется метод, который позволил бы получать решающее правило минуя стадию «ручного» анализа каждого значения W ij . По нашему мнению, такими свойствами обладают методы классификации.

Нами были проанализированы наиболее известные методы классификации, такие как метод линейной дискриминантной функции, распознавания образов, логистическая регрессия и деревья классификации [Айвазян, 1989г.; Дюк, 2001г.; Загоруйко, 1999г.; Казанцев, 1990г.; Чубукова, 2008г.]. Анализ показал, что ни один метод не может быть применен без кардинальных модификаций. Оказалось, что наиболее плодотворная идея содержится в методе деревьев классификации (ДК) – идея последовательного иерархического построения решающего правила.

Оригинальный вариант метода ДК предполагает наличие двух (или более) классов объектов, которые надо разделить на основе анализа набора показателей, характеризующих объекты обоих классов. В нашем случае два класса объектов составляют больные и здоровые дети, а показателями являются факторы риска. По сравнению с оригинальным методом деревьев классификации мы сразу отказались от варианта построения решающего правила, надежно (с высокой точностью) разделяющего здоровых и больных. Такое решение основано на том, что:

• •   надежное (100-процентное) решающее правило в нашем случае нельзя построить в

принципе, поскольку факторы риска лишь увеличивают вероятность заболевания, но не являются его причиной (хорошо известно, что больные и здоровые могут иметь один и тот же набор факторов риска);

• •    мы считаем, что для нахождения комплекса ФР, повышающего (понижающего) распространенность патологии, достаточно найти два класса детей, в которых распространенность W значительно выше (или ниже), чем в среднем по популяции;

при этом максимальная W может быть значительно ниже 100%, а минимальная W – значительно выше нуля.

Что касается конкретной программной реализации метода, нам пришлось отказаться от версии ДК, имеющейся в известном компьютерном пакете Statistica for Windows. Тому имеется две причины:

• •    в пакете Statistica разделение вершины дерева на ветви производится по критериям Джини и хи-квадрат; по нашему мнению, лучшим вариантом для решения нашей задачи является разделение по величине однофакторного эффекта ΔW (1);

• •    версия компьютерного пакета дает единственный вариант построения дерева, соответствующий экстремуму критерия Джини или хи-квадрат; мы предлагаем исследовать несколько вариантов одного ветвления, используя несколько ФР с максимальными ΔW.

В результате нами предложен алгоритм построения решающего правила, разделяющего детей с низкой и высокой распространенностью патологии [Константинова, Вараксин, 2009г.; Константинова, Вараксин, 2010г.(б)], работу которого можно продемонстрировать примером (рис. 3.).

D10

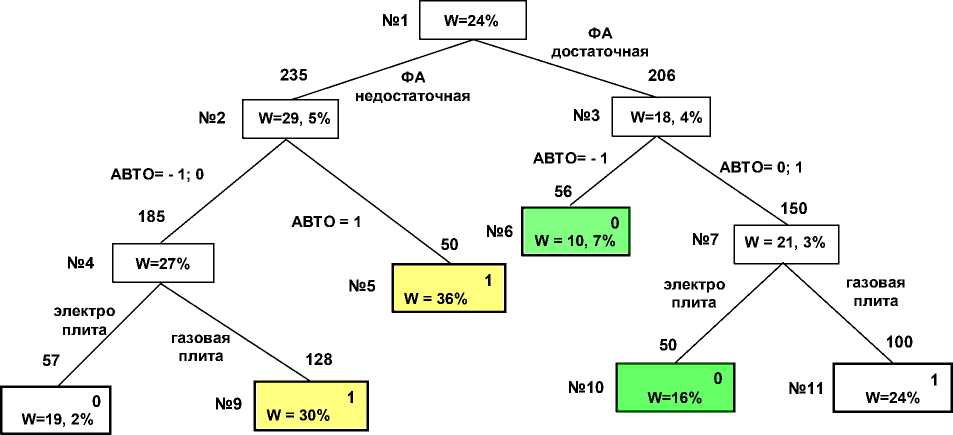
Рис. 3. Дерево классификации для заболеваний верхних дыхательных путей (класс D10)

Алгоритм работает следующим образом.

Первый этап . Построение дерева. В нашем алгоритме для каждого ветвления используется фактор, который дает максимальное различие распространенностей. На рис.6 показано, что разделение по фактору «Физическая активность ребенка – сокр. ФА» дает ΔW=29,5-18,4=11,1% (максимум из всех возможных факторов).

Второй этап. Построение набора ДК. Необходимо построить 12 деревьев, используя для первого ветвления второй и третий по величине ΔW (1) факторы, для второго ветвления используем два варианта (с помощью двух ФР с наибольшими ΔW (1) на этом этапе ветвления), а на третьем и четвертом уровнях используется один ФР с максимальным ΔW. Таким образом, для каждой изучаемой патологии для одного и того же начального списка факторов риска получается 3 ⋅ 2 ⋅ 2=12 различных деревьев классификации (задача вполне решаемая).

Третий этап. Для каждого из 12 деревьев необходимо сформировать два класса детей с низкой и высокой распространенностью исследуемой патологии. На этапе формирования классов мы предлагаем отсечь у деревьев те терминальные вершины, которые имеют W, близкую к средней для всех 441 детей W .

Четвертый этап. Для каждого из 12 деревьев надо проанализировать «качество» разделения на классы с высокой и низкой распространенностью заболевания. В нашем подходе «качество» определяется двумя показателями: значением относительного риска RR и числом детей, вошедших в решающее правило. Очевидно, что из одного дерева можно получить несколько  правил с различными значениями RR, отсекая разное число терминальных вершин; более высокие значения RR получаются при отсечении большего количества вершин, при этом сокращается число детей в классах и увеличивается неопределенность значения RR (что нежелательно).

Пятый этап. Формулировка предметно-ориентированного решающего правила (РП). Пример такой формулировки РП для данных рис. 2 приведен ниже:

В класс детей с низкой распространенностью D10 попадают дети с достаточным уровнем физической активности в сочетании с проживанием в районе с низким уровнем загрязнения воздуха либо с проживанием в квартире, в которой установлена электрическая плита (электрическая плита компенсирует негативное влияние атмосферного воздуха среднего и высокого уровней загрязнения).

Класс детей с высокой распространенностью D10 характеризуется недостаточным уровнем физической активности в сочетании с проживанием в районе с высоким уровнем загрязнения воздуха либо в квартире с газовой плитой (негативное влияние газовой плиты перевешивает проживание в районе с низким и средним уровнями загрязнения атмосферного воздуха).

Полученные выводы согласуются с данными эпидемиологических исследований о влиянии среды обитания на здоровье детей [Вельтищев, 1995г.; Чеботарев, 2007г.; Экология и здоровье детей, 1998г.]; в отличие от упомянутых работ, в нашем подходе дается количественная оценка действия на здоровье детей комплекса факторов риска.

Очевидно, что решающее правило такого типа понятно специалисту в предметной области (экологическая медицина) и позволяет выработать рекомендации, выполнение которых может снизить заболеваемость детей.

Пример рекомендации: если семья живет в районе с высоким загрязнением воздуха, желательно, чтобы в квартире была установлена электрическая (не газовая) плита; во всех случаях, сильный положительный эффект дает ориентация семьи на активный образ жизни, что позволяет ребенку иметь достаточную физическую активность.

Шестой этап. Анализ промежуточных и отсеченных терминальных вершин. Промежуточные и отсеченные вершины, не входя в решающее правило, дают важную информацию об изучаемой системе, именно о возможности компенсации действия одних ФР отсутствием других ФР [Константинова, Вараксин, 2010г.(а)].

В качестве примера системного анализа многофакторных эффектов приведем результаты анализа 12 деревьев классификации, построенных для заболеваний верхних дыхательных путей (класс D10). Показано, что для этого класса заболеваний «системообразующими» факторами риска являются загрязнение атмосферного воздуха выбросами автотранспорта, Тип плиты в квартире (электрическая/газовая) и Уровень физической активности (ФА) ребенка. Именно эти факторы встречаются ВО ВСЕХ 12 построенных для D10 деревьях классификации (ДК); именно эти факторы вместе дают наибольшую распространенность заболевания W, а их одновременное отсутствие – наименьшую W. Более того, эти факторы демонстрируют возможность взаимной компенсации. Например, в одном варианте ДК наличие достаточного уровня физической активности компенсирует негативное действие двух факторов риска – загрязненного воздуха и газовой плиты. В другом варианте ДК электроплита компенсирует наличие в квартире холода, запыленности и недостаточный уровень физической активности ребенка. Если также учесть, что уровень ФА тесно связан с образованием матери и материальной обеспеченностью семьи (см. рис. 1), получаем комплекс социальных и экологических факторов риска, образующих некую «паутину» причинности для заболеваний класса D10.

Эта паутина позволяет ответить на ряд вопросов, на которые невозможно ответить, не имея системной картины процесса. Например, вопрос: что является первичным, когда речь идет о влиянии фактора «Физическая активность ребенка» на заболеваемость детей ? Мы утверждаем, что недостаточная ФА приводит к повышенной распространенности заболевания; возможное утверждение оппонента – повышенная заболеваемость группы детей не позволяет реализоваться достаточной ФА ? Если оставаться на позициях однофакторного анализа, то вопрос останется без ответа; ответ лежит на следующем уровне, где учитываются взаимосвязи между самими факторами риска. Обратившись к ним, обнаруживаем значимую связь уровня физической активности ребенка и уровня образования матери, который можно трактовать так: более образованная мать, понимая важность для организма ребенка физических упражнений, стремится, чтобы ребенок имел достаточный уровень физической активности. В то же время, образование матери едва ли может оказать значимое влияние на распространенность таких заболеваний, которые действительно ограничивают ФА ребенка. Это позволяет высказать обоснованное предположение, что уровень ФА ребенка определяется комплексом социальных факторов семьи, а не распространенностью заболевания. Следовательно, недостаточный уровень ФА ребенка является первичным, а его следствием является повышенный уровень заболеваемости.