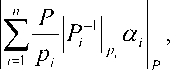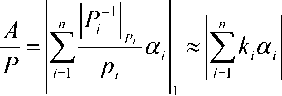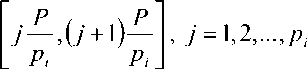;=1
– диапазон представления чисел, то есть существует число A, для которого:
A = tz, (mod pY;
A = a2(mod/?2); (2)
^«„(mod^J.
Для чисел диапазона [o, -P), представленных в видеЛ = (a1,a2,...,a„), арифметические операции сложения, вычитания и умножения выполняются с остатками ^i независимо друг от друга по простым правилам. К достоинствам такого представления и обработки чисел относится также малоразрядность остатков, что позволяет эффективно применять табличные методы обработки. Вычислительные системы, построенные на основе СОК, обладают высокой производительностью и надежностью. Однако возникают серьезные трудности при реализации непозиционных процедур, к которым относятся: нахождение вычета (остатка) числа; определение знака числа (в СОК знак числа представлен в неявном виде); сравнение модулярных чисел; определение переполнения; операции деления, масштабирования, расширения, исправления ошибок и другие. Выполнение этих операций является довольно проблематичным. Большинство приложений СОК не требуют использования этих операций. Фундаментальной операцией здесь является сравнение величины модулярных чисел, которое может быть использовано при обнаружении переполнения динамического диапазона, определения знака чисел, исправления ошибок и других, время выполнения которых может быть уменьшено до времени выполнения модульного деления вместе со сложением, вычитанием и умножением, а также масштабирования вместе с расширением.
Необходимо отметить, что даже в тех случаях, когда СОК ограничена приложениями, в которых преобладающими операциями являются сложение и вычитание, не дает возможности полностью исключить проблематичные операции. Так, в вычислениях особенно важно масштабирование, так как во многих приложениях, для которых СОК особенно хороша, могут встретиться операции, приводящие к росту чисел, которые, в свою очередь, могут привести к переполнению. Поэтому, чтобы гарантировать, что все результаты лежат в пределах допустимого диапазона, необходимо проводить контроль в процессе производимых вычислений. В связи с этим возникает необходимость быстрого выполнения вышеуказанных операций.
Кроме того, решение практически любой задачи управления требует сравнения в необходимый момент времени состояния управляемых объектов с заданными состояниями, соответствующими алгоритму функционирования систем. Целью сравнения является обнаружение факта совпадения или несовпадения значений величин, равенства или неравенства чисел, больших или меньших некоторых значений. Конкретное выполнение операции сравнения может определяться аппаратным или программным способом.
Сравнение модулярных чисел по их числовому значению может быть выполнено точно или приближенно. Прямой метод сравнения двух чисел путем перехода от остаточного представления к взвешенному представлению и затем выполнения обычного сравнения является дорогостоящим [3-4].
Основы многих алгоритмов, которые могут быть использованы для точного сравнения, базируются на следующих методах: ортогональных базисов; оценки интервалов чисел, с использованием функции Эйлера и универсальной позиционной характеристики, которая представляется коэффициентами обобщенной позиционной системы счисления (ОПСС), а также с использованием функций ранга и ядра чисел и другие. Указанные методы исследованы в работах [1-2], где показано, что в любом случае добиваются того, чтобы необходимая информация о величине числа извлекалась из представления остатков, что влечет за собой сложность как временную, так и аппаратную.
Приближенный метод вычисления основных проблемных операций в системе остаточных классов
С целью упрощения процесса сравнения модулярных чисел рассмотрим приближенный метод, который позволяет абсолютно правильно реализовать основные классы процедур принятия решений: анализ наличия определенного значения в конкретном разряде; проверка равенства (нера- венства) двух значений; сравнение двух значений (больше, меньше), которые обеспечивают решение основного круга задач, возникающих при аппаратной или программной реализации реальных процессов.
Суть приближенного метода сравнения модулярных чисел основана на использовании относительных величин анализируемых чисел к полному диапазону Китайской теоремы об остатках [4], которая связывает позиционное число A с его представлением в остатках (^\ ) ^2 5 > ^п ) ’ где а. – наименьшие неотрицательные вычеты числа относительно модулей системы остаточных классов PvP^-.Pn , следующим выражением
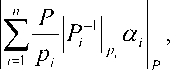
где ^Па ’ р. – модули СОК, м 1 – мультипликативная инверсия Р; относительно Pi ’ и Р
Pi = —= Р\Р--РиРм-Рп-
Pi
Если (3) разделить на константу P, соответствующую диапазону чисел, то получим прибли- женное значение
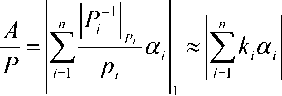
1^'1
где к, = '—^ – константы выбранной системы, а^ I – разряды числа, представленного в СОК, при этом значение каждой суммы будет в интервале [о> 1) . Конечный результат суммы определяется после суммирования и отбрасывания целой части числа с сохранением дробной части суммы. Целая часть числа представляет собой ранг числа, то есть такую непозиционную характеристику, которая показывает, сколько раз диапазон системы P был превзойден при переходе от представления чисел в системе остаточных классов к его позиционному представлению. Определение ранга будет производиться непосредственно в процессе выполнения операции суммирования констант ^-i . Дробная часть может быть записана также как A modi, потому что А = Е^]+ ^modl [5]. Количество разрядов дробной части числа определяется максимально возможной разностью между соседними числами. При необходимости точного сравнения необходимо вычислить значение (4), которое является эквивалентом преобразования из СОК в позиционную систему счисления. Для решения задач основных процедур принятия решения достаточно знать приблизительно значения чисел A и B по отношению к динамическому диапазону P, которое выполняется достаточно просто, но при этом верно определяется соотношение А = В, А > В или А < В .
Пример 1. Пусть дана система оснований А = 2, р2 = 3 , р, = 5, р, - 7 , объем диапазона Р =2-3-5•7 =210. Допустим, что в заданной СОК будут представлены только поло-
Р жительные числа. Величины Рх = — = 105,
Р\
сти. В системе остаточных классов недостаточно определить знак путем И ^\Р’ так как ^i А^
могут выходить за диапазон
2 ’ 2
и это
р Р Р
Р= —= 70, Р3= —= 42, Р4= — = 30.
" р2 Рз Ра
приведет к неправильному результату.
Пример 2. Вариант неправильного определения сравнения чисел на основе определения знака.
Р Р
Пусть А\ — ’ очевидно, что
А А
Ах > А^ . Согласно (4) определим и Ос" Р Р ’ нования СОК выберем такими же, как и в первом примере. Тогда, используя дополнительный код, получим Ах = (0,1,0,0), и Л = (о,2,0,0).
Находим
« 1-0,3333 = 0,3333;
Сравним два числа Д = 25 и А2 = 30, пред-
ставленные в СОК по основаниям Ра ■> Pl’ Рз’
Ра ’ такАх =(1,1,0,4), А, =(0,0,0,2).Для этого kt найдем константы к, = '---
Р.
^« 2-0,3333 = 0,6666. Откуда А> А р ’ ’ р р, что неверно, так как число ^2 входит в отрица-
тельный интервал, то есть
-,--1 - Сле-2 2
довательно сравнение приведет к неверному ре-зультатуАх< А2.
Для правильного определения сравнения чисел необходимо проверить знаки Ах и А-, , и тогда алгоритм сравнения будет иметь вид:
1. Определить знаки Ах и А2 .
2. Если Ах и А^ без знаков, то положительный знак разности относительных величин означает большее число.
3. Если Ах и А2 имеют один и тот же знак, то
По (4) получим
проверяется
к] А2
.
А«|1 -0,5 + 1-0,3333 +0-0,6 + 4-0,5714^ « ~ 0,1189;
^«|0-0,5 + 0-0,3333 + 0-0,6 +2-0,57141 « р 1 ’ и
4. Если
Ах и Ai
имеют разные зна-
«0,1428.
ки, то 0<
А
а2
<0,5; при Ах< А2 и
Л, А2
Таким образом,
при
2 •
сравнение чисел со знаком
А А
Так как ~^> —, то есть 0,1428 >0,1189, то
Р Р
А > Ах , и действительно 30 >25.
Рассмотрим случай, когда рабочий диапазон разбит на два интервала 0’ — – положительные - D D Л 2 У числа, и
---1 – отрицательные числа. В
2’2 )
традиционных ЭВМ определение абсолютных величин двух чисел Ах и А, производится путем вычисления А Л2 и определения знака разно- требует предварительного анализа знаков сравниваемых чисел.
Известно [2], что при кодировании дополнительным кодом отрицательная часть динамического диапазона находится у верхнего предела полного диапазона. Положительные числа из дополнительного диапазона отображаются на область о,
при нечетных P и на область о,-2
при четных P. Отображение динамичес- кого диапазона на соответствующую область для избыточного кода СОК показано на рис. 1.

Рис. 1. Схема расположения положительных и отрицательных чисел на диапазоне избыточного кода СОК
Это обстоятельство может привести к ошибке сравнения, как в вышерассмотренном примере, так как отрицательные числа попадают в верхнюю часть полного диапазона, и все отрицательные числа будут давать ошибки, что не соответствует действительности в силу разнесения динамического диапазона.
Для преодоления этой трудности необходимо произвести сдвиг отрицательной области путем вращения остаточного кольца в положение, указанное на рис. 2. Пунктиром показана область, которая перенесена в начало диапазона.

О Р-1
Рис. 2. Схема выполнения операции сдвига полярности СОК
В результате отрицательные числа будут отображены в начальной части динамического диапазона.
Показанное на рис. 2 вращение называется сдвигом полярности, и его можно осуществить путем прибавления перед сравнением модуляр-
2 при нечетном P
ных чисел константы
или С = — при четных Р к каждому ^е[О,Р) .
Если Су = |с| , то сдвиг полярности в пределах СОК оказывается простым остатком, определяемым по формуле «к. =к+с;| , в которой ос"с обозначает остаточные цифры после сдвига полярности.
Пример 3. Сравнить модулярные числа разных знаков Ау и - А2 . Система оснований СОК такая же, как и в примере 1: ^ = 2, р2 = 3 , Рз=5, р^П.
Пусть число Л, =17 = (1,2,2,3), А, =-19 = (1,1,4,5). Тогда дополнительный код А =(А-1,р2-1,р3-4.р4-5)ЦХ,2Д,2). Требуется сравнить числа Av и А2 .
Проверка знака числа ^1 . Для определения знака числа д сравним его с константой
' Тогда относительная величина числа ^1 по отношению к величине числа K определяется как Ау ~ | ку • 1 + к-, • 2 + к2 • 2 + кд • 3| — = |О,5 • 1 + 0,3333 • 2 + 0,6 • 2 + 0,5714 • 3^ » 0,0808.
Представление относительной величины р константы К = — = (1,0,0,0). Далее находим
-«10,5-1 + 0,3333-0 + 0,6-0 + 0,5714-0] =0,5.
р । 11
К А
Отсюда ---1 = 0,5-0,0808 = 0,4192. Разни-
Р Р
А. К ца положительная, то есть число —L < —, поэто-
Р Р му число т4| входит в первый интервал и является положительным.
Проверказнакачисла -/^7 проходит аналогично: ^«|0,5-1+0,33332+0,6-1+0,5714^ =0,9094 ; К А
---- = 0,5 - 0,9094 = -0,4094. Разность Р Р отрицательная, и число v42 входит во второй интервал, очевидно, что оно является отрицательным. Для правильного сравнения чисел ди ■^2 необходимо провести сдвиг полярности чисел Ау и Аэ , так как число 2^2 является отрицательным. После сдвига получаем Д = (о, 2,2,3) и А'2= (0,2,1,2).
Определим относительные величины -^1 и ^2 .
10,5-0 + 0,3333-2 + 0,6-2 + 0,5714-31 = р 1
= 0,5818;
ф « |0,5 • 0 + 0,3333 ■ 2 + 0,6 • 1 + 0,5714 • 2( =
= 0,4094.
Найдем разность относительных величин,
а'
тогда -А - ^ = 0,5 818 - 0,4094 = 0,1724 – раз-
Р Р ’ ’ ’ . .
ность положительная. Следовательнод>а2.
Рассмотренные приближенные методы определения таких позиционных характеристик модулярного кода, как определение знака числа и сравнение чисел, показали, в отличие от известных, простоту их вычисления, так как для их реализации не используется вычисление коэффициентов ОПСС, которое требует больших аппаратных и временных затрат. По этой причине данный метод представляет собой особую важность и является одним из лучших решений, по мнению автора, на настоящее время. Пере- численные операции являются важнейшими для машинной модулярной арифметики, и их применение может дать значительные преимущества не только в таких приложениях, в которых основная доля вычислений приходится на точное умножение, возведение в степень больших чисел в сочетании со сложением и вычитанием, но и в которых довольно часто появляется необходимость сравнения и определения знака числа. Известно [6], что теорема кодирования Сабо гласит, что нет лучших методов определения позиционных характеристик, при которых не используется их однозначность, чем перевод чисел из СОК в ОПСС, поскольку величины числа в модулярном представлении существенным образом зависят от всех остатков числа. Назовем этот метод определения позиционных характеристик точным методом. Однако проведенные исследования по использованию приближенных методов показали простоту определения позиционных характеристик по сравнению с методами на основе ОПСС. Таким образом, можно сделать вывод о том, что теорема Сабо справедлива только при точных методах.
Для повышения эффективности обработки данных в модулярной арифметике рассмотрим приложения приблизительных методов для определения знака числа и сравнения модулярных чисел.
Определение знака модулярных чисел
Известно [1-2; 4; 7], что для определения знака числа используются номера интервалов, в которых расположено число, что позволяет получить оценку исследуемого числа по его величине с точностью до величины интервала. Числовой диапазон P может быть разбит на Pi интервалов величиной
0,— или второй — P
. 2J 2’
половине диапазона
[o,p) . Эта задача решается сравнением данного
представления с представлением , при усло-2
вии, что Py — ^ . Все известные методы реализуют данный алгоритм на основе использования абсолютных величин, здесь же мы предлагаем использовать относительные величины, что существенно упрощает преобразование, сохраняя при этом основные функциональные возможности.
На рис. 3 приведена схема для определения знака модулярного числа, представленного по модулям /?! = 2 , p2 = 3 , Рз = 5, ^4=7. Схема содержит входные регистры RG^ Vz = [1...4] для временного хранения остатков чисел по соответствующим модулям, просмотровые таблицы LUT,, Vz = [1...4] для хранения произведений
‘ ai и параллельный сумматор. Процесс
определения интервала сводится к выявлению принадлежности данного числа к одной из двух
половин диапазона [o,p), к первой ^’~2
или
второй где принимается в качестве
. , 2
нуля. Эта задача решается сравнением относи-
A тельной величины с относительной величи-p к _ P ной P 2P 2 . Исходное число положитель-
A 1 A ное, если , и отрицательное, если
P 2 P
.
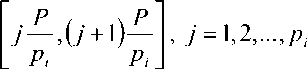
В качестве второго машинного нуля выби-p p рается точка числового диапазона Г П-У\__
2 Pn
Числа, расположенные в поддиапазонах считаются числа
O.^-l „ PP-Lp L 2 2 J I 2 p„
ми разных знаков.
Если дано представление (^1 jC^ 9,,,9^M ), то для того чтобы установить знак числа, которое оно представляет, достаточно решить задачу о принадлежности этого числа к определенному интервалу. В случае если Pi= 2 , достаточно решить задачу о принадлежности этого числа к первой
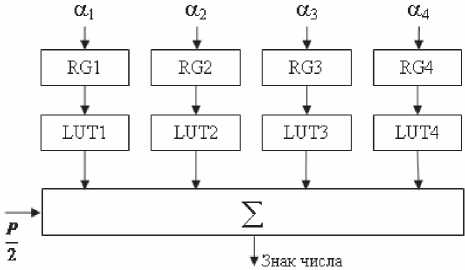
Рис. 3. Схема определения знака числа
Схема работает следующим образом.
Код числа А, для которого необходимо определить интервал, что равносильно определению знака числа, поступает на входные регистры RGj в двоичном коде (каждый разряд СОК кодируется двоичным кодом). Сигналы с выходов
регистров поступают на входы просмотровых таблиц LUT. В просмотровых таблицах хранятся произведения констант kt и остатков a, ’ то и есть ----~IZ представленных в естественной
Pi "
форме двоичной дроби в дополнительном коде. Количество элементов памяти (N) просмотровых таблиц определяется выражениемN = ^Pi.
1=1
Выходные сигналы просмотровых таблиц в дополнительном двоичном коде поступают на вход сумматора, в котором уже записана константа во время начальной установки (дополнительный код используется для того, чтобы операцию вычитания заменить операцией сложения). Знак результата сложения определяет интервал: первый или второй, что соответственно определяет знак числа.
Пример 4. Пусть дана система оснований ^i=2, p2=3, p3=5, p4=1. Тогда
^ = 210. Константы к ■ соответственно равны kx = 0,5, k2 » 0,3333, k3 =0,6, /c4 - 0,5714.
Дано: число Л = (1,1,2,0). Требуется определить знак числа A.
Решение: в регистры поместим следующие значения 7?G,=1, RG, =1, RG3=2, RG, =0. Входные значения регистров являются адресными входами LUT запоминающих элементов, которые принимают следующие значения: ЬЩ=0,5;ЬШ2 =0,3333-1 = 0,3333; LUT 3 = 10,6-2^ = 11,21, = 0,2 ; LUT4 = 0, которые поступают на вход сумматоров.
После суммирования получим:
у = |0,5 + 0,333 + 0,2|, = |0,033 |, .
Операция суммирования в данном случае может быть выполнена с помощью одноразрядного десятичного сумматора или четырехразрядного двоичного сумматора, так как младшие значения разряда на результат суммирования не имеют влияния.
Тогда --— = 0,5-0,033 = 0,467 . Разность p p ’ p положительная, то есть число A< — , откуда 2
видно, что число A входит в первый интервал и следовательно, является положительным. Определение знака осуществляется за n суммирований, где n – число оснований (модулей) СОК. Время суммирования определяется логической глубиной устройства (количество последовательно соединенных элементов) и временем суммирования в одном сумматоре. Для уменьшения времени суммирования схему сумматора можно реализовать по принципу дерева (рекурсивного сдваивания). Кроме того, реализация сумматора может быть выполнена на искусственных нейронных сетях.
Сравнение модулярных чисел
При сравнении двух чисел: A и B требуется определить, какое из них больше, меньше или они равные. Для определения номеров интервалов, в которых находятся эти числа, используются разные методы [1-2], но все они очень сложны. Пусть число A расположено в интервале 7i , а число B в интервале G . Тогда в случае 7i * Л операция сравнения может быть реализована просто сравнением номеров интервалов, а именно, если 7"i > 7"2, то A>B, если j\ то A. Исключение составляет случай 7i = 72 • Здесь для определения большего числа требуется определить номер 7з интервала, в котором расположена разность A-B. Если 0<7з<^, то разность отрицательна, отсюда A. Если Pn+\ < •
----S J3< pn, то разность положительна и
A>B.
В случае A-B = 0 числа одинаковы по величине и по знаку. Методы определения интервалов исследованы в [1-2; 7]. Все они основаны на точных вычислениях и представляют большие трудности как по аппаратным, так и по временным затратам.
Рассмотрим метод приближенного сравнения, который основан на использовании относительных значений сравниваемых чисел. Хотя предлагаемый метод является приблизительным, он позволяет достаточно просто реализовать процесс сравнения модулярных чисел с выполнением верного сравнения.
Схема модулярного сравнения чисел (рис. 4) содержит входные регистры RGA и RGB для хранения сравниваемых чисел A и B, схемы определения знаков чисел A и B (СОЗЧА и СОЗЧД логического элемента «исключающее или», схемы сдвига полярности С2СП^~1 и ССП^-!g ?просмотровые таблицы (память) LUTp A и LUTpB, / = [1..л], сумматор для сложения выходных значений LUT-таблиц и схемы сравнения знака разности для формирования сигналовA = B, AB.
На входные регистры RGA и RGB поступают исходные числа, представленные в СОК по модулямP1,P2,-,P„- С выходов регистров сигнал поступает на вход схем определения знаков числа, ССПЧД И сспчв. Выходные сигналы схем определения знаков чисел А и В поступают на вход элемента «исключающее или». При
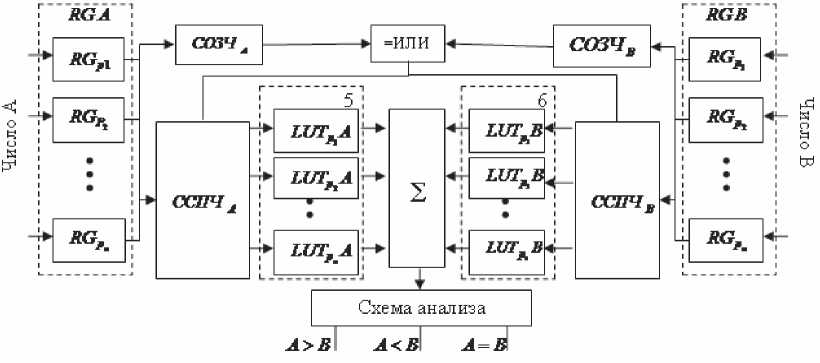
Рис. 4. Схема сравнения модулярных чисел
разных знаках чисел А и В выходной сигнал элемента «исключающее или», которому приписано значение с i ’ поступает на входы схем сдвига полярности ССПЧА и сспчв. Выходные сигналы ССПЧА и сспчв являются адресными входами просмотровых таблиц LUTpA и LUT В. Элементы памяти LUT хранят
1^'1 н
константы к, =----— а., к; =----— Д, где
Pt Pi а^АтоЛр^ fl=BmoAp., Vze[l,4].
Сигналы с выхода просмотровых таблиц LUTp A и LUT В поступают на вход сумматора, где производится взвешенное сум
А В мирование с формированием знака полученной разности чисел А и В, который анализируется в схеме анализа результата сравнения (А = В , А < В и А > В ). Рассмотрим пример сравнения модулярных чисел.
Пример 5. Пусть дана система оснований Py=^ р2=3; Р3=5; р4=1. Сравнить модулярные числа А = (1,2,2,3) и 5 = (1,2,1,2). Исходные числа находятся в регистрах RGA и RGB , которые поступают на входы схем определения знака числа СОЗЧА и СОЗЧВ.В этих схемах происходит сравнение исходных чисел с тгпттгтятттптт р константой
2 '
Определим знак числа А, для этого вычислим: ^«\к,-1 + ^2-2 + ^з-2 + ^-3^ =
= |0,5 ■ 1 + 0,3333 ■ 2 + 0,6 • 2 + 0,5714 ■ 3^ «
«0,0808;
— - - = 0,5 - 0,0808 = 0,4192.
Р Р
А К
Разность положительная, то есть поэ-
Р Р тому число А входит в первый интервал и является положительным.
Аналогично определим знак числа В.
В_
Р
\к^ • 1 + к-, - 2 + к3 • 1 + к4 • 2|^ —
|0,5 • 1 + 0,3333 • 2 + 0,6 • 1 + 0,5714 ■ 2|з «
« 0,9094
К в
Р Р12
= 0,5-0,9094 = -0,4094.
Разность отрицательная, поэтому число В входит во второй интервал и является отрицательным.
Результат определения знаков чисел А и В поступает на входы элемента «исключающее или», выходной сигнал которого поступает на вход схем сдвига полярности ССПЧА и сспчв. На выходах схем сдвига полярности образуются данные, соответственно, А = (1,2,2,3)+(1,0,0,0) = (0,2,2,3) и В = (1,2,1,2) + (1,0,0, о) = (о, 2,1,2). Выходные данные схем сдвига полярности являются адресными входамипросмотровыхтаблицLUTp A и LUT В, согласно которым осуществляется выборка зна- l^'L чений констант к; =------а; в условиях при
' Pi '
мера эти значения будут равны для LUBA (О; 0,3333-2; 0,6-2; 0,5714-3) и для LUTpB (0;0,3333-2;0,6-1;0,5714-2). Выходные сигналы просмотровых таблиц LUTpA и LUTpB поступают на вход сумматора. В результате суммирования получим:
10 + 0,3333-2 + 0,6-2 + 0,5714-31 -
P P 1 11
- 10 + 0,3333 • 2 + 0,6 ■ 1 + 0,5714 • 21( - 0,1724.
Разность положительная, следовательно A>B. Действительно, число A = \l, B = -\9.
Результаты сумматора анализируются в схеме анализа, при этом:
- если разность равна 0, то A = B,
- если разность положительная, то A>B,
- если разность отрицательная, то A.
В случае если сравниваются числа одной полярности, то из схемы сравнения модулярных чисел исключается схема определения знаков чисел. Тогда логическая глубина схемы (количество последовательно включенных элементов) будет n + 3 , где n – количество суммирований в сумматоре, при этом n определяется количеством модулей в системе.
Если же использовать рекурсивное сдваивание [1], тогда логическая глубина определяется выражением [log2/7] + 3. В известных схемах [2] логическая глубина с учетом определения коэффициентов ОПСС определяется как 2/7 + 5. Таким образом, выигрыш в скорости предложенного метода почти равен двум.
Итак, разработанный метод и аппаратная реализация определения знака числа и сравнения модулярных чисел является одним из лучших на настоящее время по показателям сложности и скорости.
Предложенный метод может быть использован для определения переполнения динамического диапазона и определения ошибок в избыточных системах остаточных классов. Если в избыточной СОК в качестве рабочих оснований принять Pl, Pl, ■•; P„, а в качестве избыточных основа ний Pn+\, Pn+2, ••', Pn+r, разрешимые значения определяются как ^^A. Факт переполнения /=i или ошибки определяется сравнением проверяемого числа A с рабочим диапазоном P: если A>P, то произошло переполнение или ошибка. Одиночная ошибка может быть обнаружена так же, как и переполнение динамического диапазона, при предположении, что переполнение не происходит одновременно с ошибкой.
Выводы
1. Противоречие между вычислительной сложностью определения основных проблемных процедур в СОК и их быстродействием
2. Решена фундаментальная проблема реализации основных проблемных операций в СОК, которые ранее определяли наибольший вклад в алгоритмическую сложность и сдерживали широкое применение СОК при разработке новых классов вычислительных систем. Внедрение полученных результатов позволяет снять это ограничение и расширить область применения модулярной арифметики.
3. Разработанные методы, алгоритмы и техническая реализация самых проблемных процедур, характеризующихся простотой и высокой скоростью выполнения операций, дополняют известный универсальный базис СОК на основе обобщенной позиционной системы счисления и позволяют разделить выполнения всех немодульных процедур на два класса: процедуры точного вычисления (вычисления остатка, округления числа, деления, масштабирования, расширения модулярной величины на дополнительные основания и коррекция ошибок) и процедуры приблизительного вычисления (сравнения модулярных чисел, вычисления ранга числа, определения знака числа и переполнения диапазона, обнаружение и локализация ошибок при кодировании помехоустойчивым кодом). Перечисленные классы процедур являются важнейшими для машинной модулярной обработки и требуют глубокого дальнейшего исследования для определения границ их эффективного применения.
4. Полученные новые результаты эффективного выполнения немодульных процедур являются развитием теории математических основ разработки и проектирования высокопроизводительных и надежных вычислительных систем, функционирующих в системе остаточных классов.
разрешена путем замены абсолютных величин их относительными значениями и простотой их вычисления, которая сохраняет адекватную связь числовых значений модулярных величин с их представлениям в СОК и позволяет повысить скорость выполнения немодульных операций. Благодаря этому применение системы остаточных классов может дать значительные преимущества не только в тех приложениях, в которых основная доля вычислений приходится на точное умножение, возведение в степень больших чисел в сочетании со сложением и вычитанием, но и в которых часто появляется необходимость в делении либо сравнении и определении знака числа, а также при проверке не «выходят» ли результаты за пределы допустимых значений и другие.