Методы аппроксимации тепловых карт Wi-Fi

В высшей математике доказано много разнообразных способов аппроксимации функции, заданной таблично, которые описаны достаточно точно в специальной математической литературе. Разнообразие методов аппроксимации объясняется различными требованиями к точности приближающей функции: минимум среднеквадратической оценки, минимум максимума модуля невязки, точное (с заданной погрешностью) совпадение в интерполирующих узлах и т.д [1].

Рассмотрим один экспериментальный метод аппроксимации функции от двух переменных, значения которой получены в ходе измерений и, следовательно, обладают некоторым разбросом. Для данного примера точность аппроксимации будет считаться достаточной, если исследование удовлетворит величина полученной среднеквадратической ошибки.

В данном исследований необходимо построить тепловую карту Wi-Fi сигнала по входным данным. В ходе исследования необходимо аппроксимировать функцию от двух переменных. Таким образом, целевая функция представляет собой зависимость уровня сигнала беспроводной сети от плоских прямоугольных координат – абсциссы и ординаты.

Ряд работ [2], [3] посвящён поиску нестандартных решений для аппроксимации.

Метод Брандона [4] хорошо отражает, тот факт, что аппроксимация целевой функции от нескольких переменных может сводиться к аппроксимации зависимости от нескольких пар переменных. Смысл метода состоит в следующем. Рассматривается совокупность значений зависимой переменной - и значений одной из независимых переменных X1 . Из определенного заранее группы функций выбирается такая, которая наилучшим образом — в смысле минимума среднеквадратической ошибки — приближает видимую зависимость между -и ■Ч .

На следующем шаге алгоритма находится функция, приближающая видимую зависимость между 1и 2 , и т.д. Группа функций, из которых берется наилучшая, определяется исходя из поставленных задач, то есть составляется из тех функций, которые соответствуют природе изучаемых зависимостей.

Обобщая вышесказанное, можно утверждать, что метод сводится к многократному нахождению зависимостей между двумя переменными, которые определяем методом наименьших квадратов, так как он наиболее удобен из-за простоты вычислений, хорошо аппроксимирует и усредняет разброс значений зависимой переменной. Коэффициенты приближающей функции на 1 -м этапе АСч должны удовлетворять каноническому условию метода наименьших квадратов.

В данном исследовании ставится задача показать эффективность метода аппроксимации от степени аппроксимирующей функции. Для данного исследования необходимы исходные табличные значения. Для упрощения ввода точек их можно сгенерировать случайным образом опираясь следующие параметры источников беспроводной сети: ширина поля, высота поля, максимальное значение уровня сигнала и скорость падения или уменьшения сигнала. Ниже приведен рисунок сгенерированной тепловой карты (Рисунок 1).

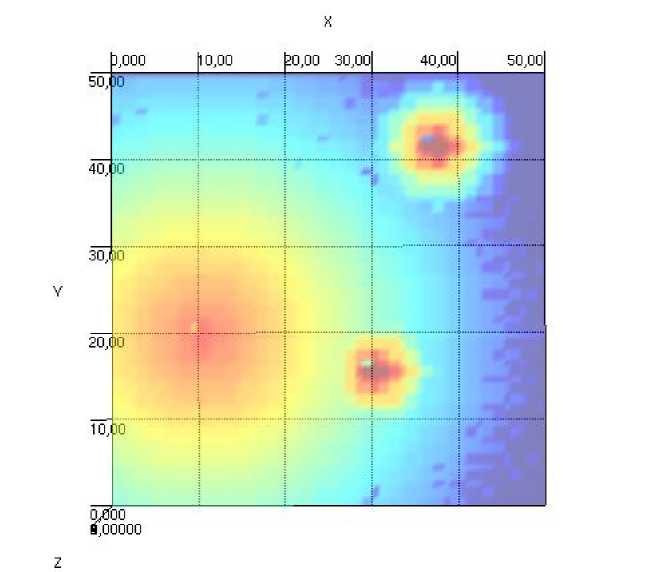
Рисунок 1 – Сгенерированная тепловая карта

Для аппроксимации разобьём нашу сгенерированную плоскость на фрагменты по одной из переменной, например по оси x. В результате получим значения в некоторых точках нашей целевой функции от одной переменной. Получим фрагментированный график отражающий зависимость уровня сигнала от одной координаты (рисунок 2).

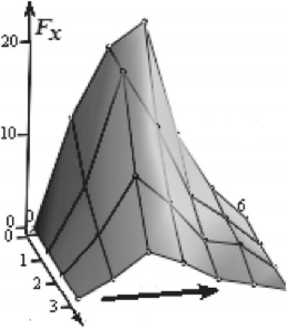
Рисунок 2 – Фрагментация уровня сигнала по одной из осей

Следующим этапом аппроксимируем полученные значения функций полинома методом наименьших квадратов. Геометрически это значит, что нужно найти кривую y = F(x), полином, который проходит как можно ближе к каждой из заданной точек.

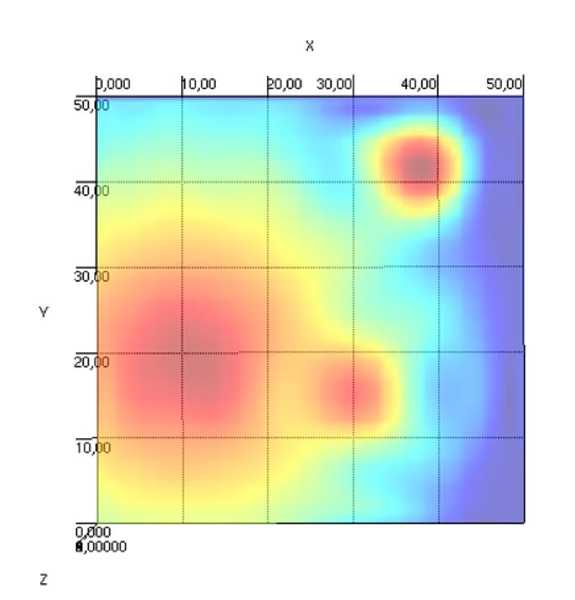
Рисунок 3 – Аппроксимированный график функции двух переменных

После проделанных вычислений по всей оси x переходим к оси y. Для нее исходные данные в точках пересечения фрагментов будут значения, которые получились при аппроксимации по оси x. Вычисления при приближении по оси y аналогичны вычислениям по оси x. Результат такой аппроксимации приведен на рисунке 3.

Так как нам необходимо, построение гладкой тепловой карты, то в программе предусмотрено ввод параметра «множитель точек». Программа позволяет определить зависимость между степенью полинома и среднеквадратичной погрешностью.