Методы формирования профиля поверхности дифракционных оптических элементов
Автор: Полещук А.Г.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 16, 1996 года.
Бесплатный доступ
Приводится обзор результатов исследования фотолитографического метода изготовления высокоэффективных дифракционных оптических элементов (ДОЭ), основанного на применении только одного фотошаблона с двумя градациями пропускания. Для бинаризации непрерывной функции пропускания дифракционного элемента применена техника растрирования полутоновых изображений, а для экспонирования светочувствительной среды - некогерентная пространственная фильтрация в сочетании с обычным фотолитографическим процессом. Анализируется зависимость дифракционной эффективности ДОЭ от параметров фотошаблона, методов бинаризации и погрешностей изготовления. Проведено сравнение характеристик предложенного метода с известным - многоуровневым методом. Рассмотрены особенности изготовления ДОЕ с непрерывным фазовым профилем, основанные на проекционной, контактной и рентгеновской литографии. Приведены результаты экспериментального исследования. Показана возможность изготовления ДОЭ с дифракционной эффективностью более 80% с помощью только одного фотошаблона.
Короткий адрес: https://sciup.org/14058330
IDR: 14058330
Текст научной статьи Методы формирования профиля поверхности дифракционных оптических элементов
В настоящее время прогресс в оптике связывается с широким применением компьютерно синтезированных дифракционных оптических элементов (ДОЭ). Эти элементы представляют собой тонкие рельефно-фазовые структуры и широко используются в оптических цифровых компьютерах, оптической памяти, дисплеях, датчиках и т.д. [1,2,3]. Их потенциальные возможности во многом определяются технологией изготовления, которая должна обеспечивать максимум дифракционной эффективности (ДЭ) и отношения сигнал - шум в формируемом оптическом сигнале.
В настоящее время известно несколько методов изготовления ДОЭ. Прямая запись сфокусированным излучением лазера или пучком электронов по тонким пленкам резистов позволяет изготавливать высококачественные и высокоэффективные ДОЭ [4]. Однако каждый изготовленный элемент уникален, так как требует отдельной записи, а для тиражирования необходима технология репликации.
Метод фотолитографии позволяет достаточно просто изготавливать и тиражировать ДОЭ с бинарным фазовым профилем. Комплект из 3-4 фотошаблонов дает возможность получить много- уровневые (М=8-16) ДОЭ с ДЭ более 95% [3]. По своим оптическим параметрам эти элементы могут конкурировать с элементами классической оптики.
Полутоновой метод позволяет изготавливать высокоэффективные ДОЭ с использованием одного полутонового фотошаблона [5]. При этом отпадает необходимость в совмещении фотошаблонов, а минимальные размеры фазового профиля определяются только процессом литографии [6].
Иной путь создания фазового профиля ДОЭ основан на когерентной пространственной фильтрации спектра бинарного периодического шаблона и отбеливании экспонированной пленки [7]. Этот метод значительно упрощает процесс создания ДОЭ, так как не требует изготовления комплекта шаблонов и его совмещения. Однако этим методом изготавливаются только ДОЭ с периодической структурой.
Микрорельеф ДОЭ с непрерывным профилем может быть сформирован с использованием рас-трированного фотошаблона и проекционной оптической системы, осуществляющей некогерентную пространственную фильтрацию растрирован-ного изображения. Этот метод, получивший название "Фоторастровый метод" (Half-tone mask technique), позволяет изготавливать высокоэффективные ДОЭ с непрерывным фазовым профилем, используя коммерческое оборудование для микроэлектроники. Впервые этот метод был предложен [6,8,9] для изготовления киноформных микролинз и корректоров аберраций, а в дальнейшем начал широко применяться для изготовления мик-ролинзовых растров и других ДОЭ [10, 11]. Простота фоторастрового метода в сочетании высоким качеством изготавливаемых элементов делает его одним из наиболее удачных методов изготовления ДОЭ.
В настоящей работе приводится обзор результатов исследования фоторастрового метода изготовления высокоэффективных ДОЭ основанного на применении техники растрирования полутоновых изображений и некогерентной пространственной фильтрации в сочетании с обычным фотолитографическим процессом [12]. Проведено сравнение характеристик метода с известным - многоуровневым методом. Рассмотрены особенности изготовления ДОЕ с непрерывным фазовым профилем, основанные на проекционной, контактной и рентгеновской литографии. Приведены результаты экспериментального исследования.
-
2. Фоторастровый метод.
Задача изготовления чисто фазового ДОЭ (киноформа) с функцией пропускания
T (x ) = exp [- M x)] (1)
решается формированием в подложке рельефа (пропускающий ДОЕ)
h ( x ) = (2) П 11
где k =2 n / X , X - длина волны, n - коэффициент преломления. Из теории фотолитографии известно [12], что при экспонировании позитивных резистов излучением с интенсивностью I ( x ), толщина оставшегося после проявления слоя резиста равна
hd (x) = Do ~ YI (x) (3)
где D o -толщина исходной пленки, с - коэффициент, учитывающий продолжительность экспозиции, проявления и другие параметры резиста. Из выражений (2) и (3) следует, что если распределение интенсивности I ( x ) пропорционально фазовой функции ϕ( х ), то в слое фоторезиста после экспонирования и проявления сформируется ДОЭ с функцией пропускания T ( x ).
Как сформировать такое распределение? Один из известных путей заключается в использовании полутонового фотошаблона с функцией пропускания U ( x ) ~ ф ( x ). Но изготовить такой шаблон по техническим причинам трудно [5]. В фоторастровом методе используется растрирование полутоновых изображений, широко используемое в полиграфии, системах отображения информации, технике связи и т.д.. Растрирование изображения - это процесс преобразования пространственного полутонового распределения интенсивности I ( х ) в двухуровневое (бинарное) изображение В ( х ) [13]. Характеристики восстановленного изображения зависят от вида процедуры кодирования, т.к. на практике форма отсчетов отличаются от ст - функций и имеют вид прозрачных участков (полосок для одномерного и квадратов или точек различного размера для двумерного случаев) конечной ширины на непрозрачном фоне. Для кодирования полутонового изображения наиболее часто используют частотно-импульсную (ЧИМ) и широтноимпульсную (ШИМ) модуляцию функции пропускания фотошаблона. Очень хорошие результаты дает алгоритм рассеяния ошибок (errors diffusion algorithm).
В предлагаемом нами фоторастровом методе [6,8,9] непрерывный фазовый профиль формируется за один технологический цикл с использованием серийного фотолитографического оборудования. Процесс изготовления включает следующие основные этапы:
-
• Расчет функции пропускания ДОЭ (см. выражение (1)) и полутоновой функции U ( x ) ~ф ( x ).
-
• Растрирование полутонового изображения: B ( x )=V[ U ( x )], где V- оператор, преобразует непрерывную функцию U ( х ) в бинарную В ( х ).
-
• Изготовление фотошаблона с бинарным пропусканием.
-
• Экспонирование слоя фоторезиста системой фотолитографической установки. Распределение интенсивности экспонирующего излучения: I ( x )= B ( x ) * O ( x ), где О ( х )- импульсный отклик оптической системы.
-
• Проявление фоторезиста и формирование рельефа (выражение (3)). Время экспозиции и проявления (коэффициент γ) выбираются из условия h dmax = k X /(n -1), где k =1,2,3....
Фоторастровая технология позволяет использовать обычные фотошаблоны с двухградационным пропусканием. Такие бинарные фотошаблоны можно достаточно просто изготовить с помощью обычных лазерных или электронно - лучевых генераторов изображений. Оптическая проекционная система фотолитографической установки используется как фильтр пространственных частот растрирован-ного изображения и формирует распределение интенсивности в плоскости резиста достаточно близкое к исходной функции.
Возможно несколько вариантов фоторастрово-го метода, отличающихся, главным образом, способом экспонирования слоя резиста.
Проекционный метод. Метод основан на использовании установки проекционной фотолитографии [12]. Растрированный фотошаблон освещается некогерентным световым потоком (Рис. 1а). Проекционная оптическая система формирует в плоскости пластины с резистом сглаженное распределение интенсивности близкое к функции ϕ( х ). Соотношение пространственных частот среза оптической передаточной функции (ОПФ) F c проекционного объектива с числовой апертурой NA , растрирования фотошаблона F d и спектра G ( f x ) функции U ( x ) показаны на Рис. 1б. Согласно теореме отсчетов должно выполняться неравенство f x < F c < F d . При этом в результате пространственной фильтрации в выходном спектре G 2 ( f x ) отсутствуют пространственные частоты дискретизации F d. Необходимо отметить, что высота рельефа в резисте ограничена глубиной резкости проекционного объектива D = X / NA 2 [12] и для типичных значений X =436 nm и NA =0.35 не превышает D =3 мкм.
Теневой метод. В этом, наиболее простом, методе фотошаблон и пластина с резистом находятся на расстоянии d друг от друга. Свободное пространство между фотошаблоном и резистом (до нескольких десятков микрон) необходимо для осуществления усреднения (сглаживания) локальной I си( x ) = R ( x ) ® B ( x ).
В принятой модели импульсный отклик определяется распределением интенсивности излучения источника спроектированным в исследуемую плоскость: R(x) = exp[-(mx)2 / /ст2], где m = d/L - масштабный коэффициент. На Рис. 2б приведены результаты моделирования распределения интенсивности излучения после прохождения шаблона на различном расстоянии от поверхности резиста. Функция пропускания шаблона - растрированная пилообразная функция c периодом Т. Видно, что на расстоянии d4 ~ 60мм распределение излучения близко к заданному, пилообразному. Этот метод имеет очень большую глубину резкости и позволяет изготавливать ДОЭ с глубоким профилем, как на плоских, так и на криволинейных поверхностях, например поверхностях линз или зеркал.
Проекционный метод изготовления ДОЭ. Фотолитографическая установка (а) и преобразование пространственного спектра растрированного фотошаблона (б).
Некогерентное
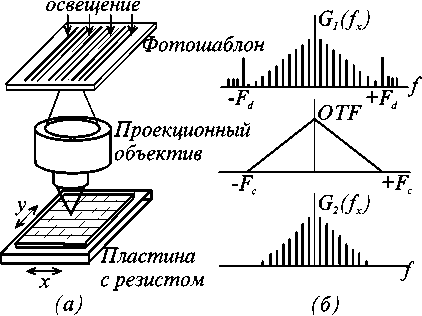
Рис. 1.
Теневой метод изготовления ДОЭ. Устройство рентгеновской литографии (а) и распределения интенсивности экспонирующего излучения в плоскости резиста (б).
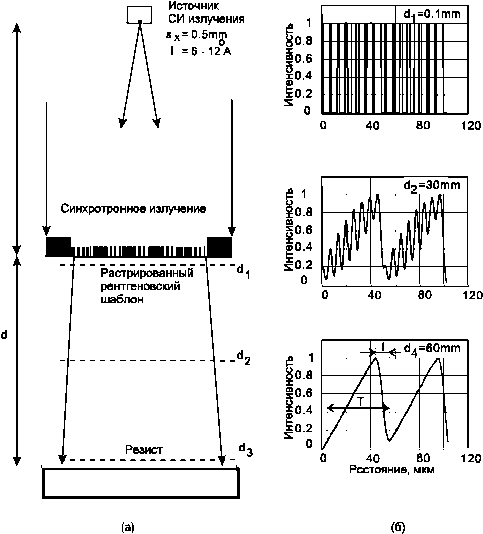
Рис. 2.
Дифракционная эффективность. Из-за конечных размеров импульсного отклика оптической системы литографической установки, форма профи- ля в резисте отличается от исходной. Для того чтобы получить высокую ДЭ необходим пилообразный профиль с как можно меньшим обратным склоном. Потери световой энергии на этом участке могут быть оценены как 2L/T, где L=0.61X lit/NAlit - размеры обратного склона, T - период решетки, коэффициент 2 введен в соответствии со скалярной теорией дифракции. Один из простейших, но широко распространенных ДОЭ - киноформная линза представляет собой дифракционную решетку с пилообразным профилем и минимальным периодом Тmin=XDOE/NA DOE. Дифракционная эффективность такой линзы связана с ее параметрами (рабочая длина волны - XDOE и числовая апертура - NA DOE ) и параметрами установки фотолитографии (длина волны экспонирующего резист излучения - X lit и числовая апертура проекционного объектива - NАlit ) выражением:
П = | 1 - 1.22 XitNADOE 1 100%. (4) I X doe NA h. J
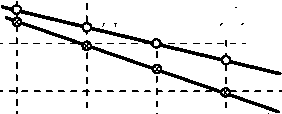
Зависимости ДЭ киноформной линзы от величины ее числовой апертуры приведена на Рис. 3. Кривые рассчитаны для проекционной системы литографической установки с числовой апертурой NA =0.35 и длиной волны экспонирования, соответственно, 300 и 436 nm. Выражение (4) позволяет оценить максимально возможную эффективность линзы изготовленной методом проекционной фотолитографии. Анализ и эксперименты показали, что ДЭ и NA киноформных линз и других ДОЭ определяется главным образом пространственным разрешением литографического процесса.
Дифракционная эффективность ДОЭ, изготовленных методом проекционной фотолитографии
= 100
5 80
^,40 ф 20
] Проекционная оптическая
| система с Н.А. =0,35
I Длина волны, X, пт:
"300
0 0,05 ОД 0,15 0,2 0,25
Числовая апертура линзы, Н.А.
Рис. 3.
-
3. Формирование фазового рельефа
Исследовались два метода получения непрерывного фазового профиля ДОЭ - с использованием алгоритмов ЧИМ и ШИМ [6, 9] В качестве исходной фазовой функции ϕ( х ) была выбрана простейшая - пилообразная.
При бинаризации по методу ЧИМ, пространственная частота следования импульсов (в дальнейшем -полосок, имеющих постоянную ширину а ) пропорциональна значению функции U ( x ). Вводя коэффициент глубины модуляции Р m =( F max - F min )/( F max - F min ), выражение для частоты следования можно записать в виде
F pdm = F m { 0,5 + P m [ ^ ( X ) - 0,5 ] } (5)
где F m=2 F min/(1+ Р m), а частота следования F pdm изменяется в пределах от F max до F min .
В методе ШИМ, пространственная частота следования полосок растра постоянна, а их ширина l (в двумерном случае - площадь) пропорциональна значению кодируемой функции ϕ(х) в точках i дискретизации li= Td {0,5 + Pm [^ (x - iTd)-0,5]} (6)
Здесь T d=1/ F d - период дискретизации, i = 1,2,3.. m - номер полоски, P m=( l max- l min)/( l max+ l min) - глубина модуляции, l mах и l mах - максимальная и минимальная ширина импульсов на периоде функции U ( х ) .
Если исходное изображение является периодической функцией с периодом Т, то функцию пропускания фотошаблона растрированного методом ЧИМ с учетом погрешности Ri нанесения i-той полосы растра можно записать в виде та m
B ( x ) = a ( x ) * ^E 5 [ X - ( nT - T - ^ i ) ] (7)
n =-та I =1
где a ( x )-функция пропускания элементарной полоски, m -число полосок растра на периоде исходной функции, T , =1/ F pdm, * - оператор свертки.
Аналогично, функцию пропускания фотошаблона растрированного ШИМ можно записать в виде та m
B ( X ) = ZZ a ( X ) * 5 ( X - iTd - nT ) (8)
n =-та I =1
где a i ( x )-функция пропускания i -той элементарной полоски, имеющей ширину l i + R i .
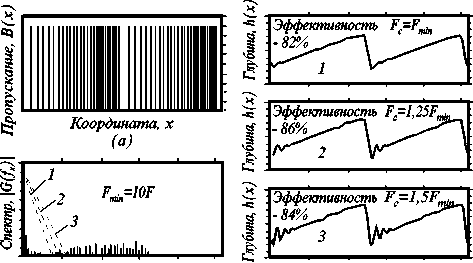
На Рис. 4а,б показаны, соответственно, функция пропускания растрированного методом ЧИМ фотошаблона (при численном моделировании период исходной функции был выбран равным 512 точек) и ее модуль спектра интенсивности | G(f x ) | (в расчетах использовался алгоритм БПФ). Видно, что в области нижних частот спектр соответствует спектру пилообразной функции, а в области средних и верхних частот, содержит комбинационные составляющие. На Рис. 4в показана форма рельефа (выражение (3)) для трех значений положения частоты F c среза ОПФ (пунктирные линии) при одинаковом периоде T =1/ F исходной пилообразной функции. С ростом F c форма рельефа h d ( x ) приближается к пилообразной. Видно, что бинаризация исходной функции U ( x ) приводит к появлению искажений (волнистости), которые особенно хорошо видны при F c >> F min .
Функция пропускания растрированного методом ЧИМ фотошаблона (а), ее пространственный спектр (б) и форма рельефа поверхности резиста (в,г).
Пространственная частота, f Координата х
(б) (в) '
Рис. 4.
На Рис. 5а,б показаны, соответственно, функция пропускания (8) растрированного методом ШИМ шаблона и модуль его пространственного спектра. Пространственный спектр шаблона на частоте F d имеет значительную составляющую, обусловленную дискретизацией. На Рис. 5в показана форма рельефа в фоторезисте рассчитанная для двух значений F c / F d . Видно, что даже при незначительном увеличении частоты среза ОПФ резко возрастают периодические искажения рельефа ДОЭ и уменьшается ДЭ. Сравнивая кривые на Рис. 4 и 5 видно, что метод растрирования ЧИМ менее чувствителен к ошибкам положения частоты среза ОПФ проекционной системы.
Функция пропускания растрированного методом ШИМ фотошаблона (а), ее пространственный спектр (б) и форма рельефа поверхности резиста
(в,г).

Координата, х (а)
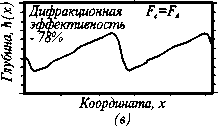
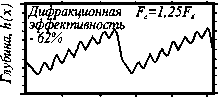
Координата, х (г)

\ 1 F,=8F
\
Пространственная частота, fx
Рис. 5.
Одним из основных параметров ДОЭ является ДЭ, которая определяется количеством отсчетов при дискретизации функции пропускания фотошаблона (в многоуровневом методе - это количество уровней квантования фазы). На Рис. 6 показаны фрагменты фотошаблонов (одномерная решетка с "блеском") растрированные методом ШИМ с, соответственно, 4, 8 и 16 отсчетами на период функции (а), форма рельефа формируемая в фоторезисте методом проекционной литографии (б) и пространственные спектры дифракционной решетки с таким профилем (в). Видно, что ДЭ превышает 87% при 16 отсчетах функции на периоде.
Фрагменты растрированных методом ШИМ фотошаблонов, форма рельефа в фоторезисте и распределение интенсивности светового потока дифрагированного на этой решетке.
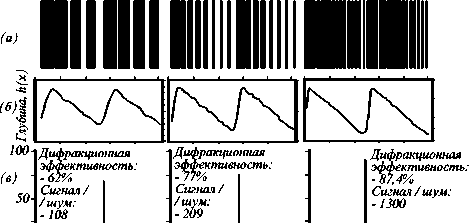
Рис. 6.
Все этапы изготовления ДОЭ вносят ошибки, которые существенно влияют на его характеристики. Основные ошибки при изготовлении ДОЭ фото-растровым методом следующие :
-
• положение границ линий растра;
-
• искажение ОПФ проекционной системы;
-
• неправильная величина экспозиции;
-
• нелинейность фоторезиста и др.
-
4. Формирование фазового профиля многоуровневым методом
На Рис. 7 приведена зависимость ДЭ решетки с пилообразным профилем как функция от числа m = F c / F прошедших проекционный объектив (Рис. 5б) пространственных гармоник экспонирующего резист излучения I ( x ). Моделировалось влияние случайных ошибок σ=ε/ T положения краев линий растра (метод ШИМ). Кривая для σ=0 соответствует идеальному случаю - отсутствию ошибок изготовления. С ростом ошибок, ДЭ резко падает. Если считать приемлемым падение ДЭ на 5% от идеала, то относительная допустимая среднеквадратичная ошибка изготовления растра лежат в пределах δ<0.004. При размере зон растра T =3-5 мкм, среднеквадратичная ошибка должна быть ε<0.01-0.02 мкм. Типичная величина ошибок при изготовлении фотошаблонов [12], лежат в пределах 0.1-0.5 мкм, т.е. в 5-10 раз больше допустимого. Наилучший метод уменьшения ошибок изготовления - это изготовление фотошаблона в увеличенном масштабе (обычно 10:1), а затем проекционное экспонирование с уменьшением в 10 раз. Это позволяет легко достичь требуемой точности.
Фотолитографический многоуровневый метод изготовления ДОЭ включает в себя подготовку комплекта фотошаблонов, а затем последовательный перевод их топологии в рельеф подложки. Если на каждом шаге подложка травится на одинаковую глубину (вариант I), равную λ/(n-1)M, то требуется m=М-1 шаблонов с одинаковым периодом зон Т. Если глубина травления (вариант II) зависит от порядкового номера i фотошаблона hi=λ⋅2i-1/M(n-1), а период зон изменяется по закону Ti=Τ⋅2ι-1/M, то требуемое число шаблонов для достижения заданного M уменьшается : m=log2M [3].
Зависимость дифракционной эффективности решетки с пилообразным профилем от числа пространственных гармоник. Решетка изготовлена фоторастровым методом.
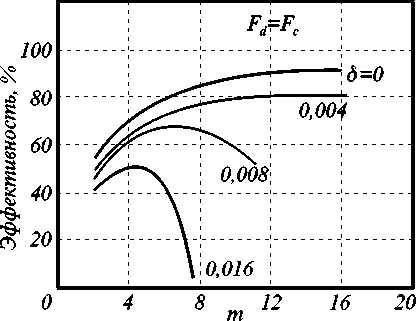
Рис. 7.
При изготовлении ДОЭ, функцию описывающую глубину рельефа можно представить в виде:
N
h (x) = D0 -Е h (x - ^ , ^1, ^h , dk )
=1
Функция h i ( x ) - соответствует форме рельефа подложки ДОЭ после i -го шага травления.
Параметры σx, σl, σh, d k - характеризуют, соответственно, ошибки совмещения, погрешности выполнения границ фотошаблона, глубины и клина травления. Так как ошибки вносимые каждым фотолитографическим циклом практически независимы друг от друга, то погрешности σ x , σ l , σ h описываются нормальным законом распределения вероятностей, а величина клина травления d k - одинакова для всего процесса. На Рис. 8 представлены результаты моделирования (выражение (11)) формообразования одномерной пилообразной решетки двумя разновидностями многоуровневого метода (а) и зависимость ДЭ одной из таких дифракционных решеток от среднеквадратичной ошибки изготовления (б). В расчетах использовались безразмерные параметры: δ x =σ x / T и δ l =σ l / T нормированные к периоду T пилообразной решетки. Видно, что второй вариант многоуровневой технологии чувствительней к случайным технологическим ошибкам.
Хотя влияние ошибок совмещения и изготовления фотошаблона приблизительно одинаково, следует учитывать, что обычно фотошаблоны изготавливаются в увеличенном масштабе, а затем уменьшаются до необходимых размеров. При этом ошибки изготовления пропорционально уменьшаются и становятся незначительными.
Клин травления зависит от технологии изготовления ДОЭ. Он равен высоте h i ступеньки (около 0.2 мкм при m =8 для ДОЭ видимого диапазона) при жидкостном изотропном травлении и приблизительно на порядок меньше при ионно-лучевом. Однако даже незначительная величина клина приводит к падению ДЭ. Это можно объяснить сглаживанием ступенек аппроксимирующей функции. Влияние клина травления аналогично фильтрующему действию ОПФ проекционного объектива при изготовлении ДОЭ фоторастровым методом. Незначительное влияние на падение ДЭ оказывают случайные погрешности глубины травления ступенек. Вполне допустимыми являются погрешности порядка 3-5%, которые достаточно легко выполняются на практике.
Фазовый профиль (а) штрихов пилообразной решетки изготовленной двумя разновидностями многоуровневого метода и зависимость (б) дифракционной эффективности от величины ошибок изготовления (метод 2).
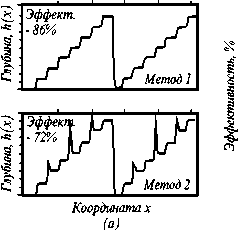
Рис. 8.
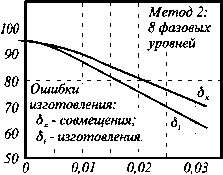
Среднеквадратичная ошибка (6)
-
5. Сравнение фоторастровой и многоуровневой технологий
Различные технологии обычно сравниваются по двум основным критериям - по достижимому эффекту и затратам на его получение. Дифракционная эффективность является одним из основных критериев оценки метода изготовления ДОЕ.
С учетом погрешностей реального литографического оборудования (уменьшение 1:10, проекционный объектив с NA=0.35) моделировалось изготовление дифракционных решеток с пилообразным профилем фоторастровым и многоуровневым методами. Периоды решеток равнялись: 5, 20 и 100 мкм. Среднеквадратичные значения ошибок изготовленияё: σx=0.1мкм, σl=0.05мкм для многоуровневого и ε = 0.1 мкм для фоторастрового методов. Результаты расчетов приведены на Рис. 9. Видно, что фоторастровая технология позволяет получить большую ДЭ при изготовлении фазовых решеток с периодом менее 20 мкм. При больших периодах решетки (100 мкм и более), многоуровневая технология (M=8) имеет некоторое преимущество. Однако с точки зрения затрат, фоторас-тровый метод более предпочтительней. В этом методе используется только один фотошаблон, нет необходимости в совмещении и многократном травлении подложки. К его недостаткам следует отнести необходимость в проекционном оборудовании, зависимость результата от качества фоторезиста и условий проявления, принципиальное ограничение ДЭ размером импульсного отклика проекционного объектива (обратный склон, см. Рис. 3) и т.д.
Сравнение методов изготовления ДОЭ.
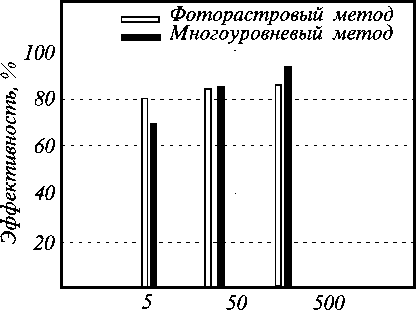
Период решетки, мкм
Рис. 9.
-
6. Экспериментальное исследование.
Целью экспериментального исследования было подтверждение возможности получения фоторас-тровым методом микрорельефа ДОЭ с заданной формой и характеристиками.
Фотошаблон . Для дискретизации полутоновой функции нами использовался алгоритм ШИМ
Растрированные фотошаблоны изготавливались с помощью кругового лазерного генератора изображений (КЛГИ) [15] на стеклянных подложках покрытых пленкой хрома. Минимальная ширина кольцевых зон растра фотошаблона определялась пространственным разрешением КЛГИ и технологией записи (минимальная ширина записываемых линий около 0.6-0.8 мкм) и составляла около l min=1,2 мкм. Это определило величину периода растрирования T d =6мкм (глубина модуляции P m =0.6). Изготавливались растрированные фотошаблоны линейных решеток , киноформных линз и киноформных корректоров аберраций [6, 8, 9, 16, 17] для экспонирования как проекционным (уменьшение 10 раз), так и теневым методами (1:1). Фотошаблоны представляют собой линейные или круговые решетки с линиями переменной ширины (от 1.2 до 4.8 мкм). Микрофотографии участков поверхности одного из растрированных фотошаблонов показаны на Рис. 10.
Для экспериментов по рентгенолитографии, растрированные шаблоны изготавливались на мембране из нитрида кремния толщиной 2 мкм [14]. Толщина золотого покрытия - 0.6 мкм.
Микрофотографии фрагментов поверхности растрированного фотошаблона киноформной линзы. Участки центральной (а) и периферийных зон линзы (в), микрофотография скола хромового фотошаблона полученная с помощью электронного микроскопа (б) и увеличенный фрагмент (г) растрированных зон линзы (граница соседних зон ДОЭ), Период растрирования равен 6 мкм, неровность края 0.1 мкм.

Рис. 10.
Экспонирование . Микрорельеф ДОЭ формировался проекционным методом в слое фоторезиста ФП-051 МК толщиной около 2 мкм, а затем ионным травлением переносился в материал подложки. Уменьшение изображения фотошаблона и его мультиплицирование осуществлялось на стандартной установке проекционного экспонирования UER (объектив NA =0,35). Глубина рельефа в фоторезисте определялась величиной экспозиции. Для получения необходимой глубины рельефа, экспозиция в процессе мультипликации изменялась в небольших пределах при переходе от одного элемента к другому. На Рис. 11 показаны профилограммы (профилограф Taylestep) центральной части (а) дифракционного корректора и его крайних зон (б), имеющих минимальные размеры порядка 7 мкм. Видно, что форма зон близка к заданной - пилообразной.
Профилограммы поверхности киноформной линзы изготовленной фоторастровым методом.
a
100 цт


