Методы формирования векторов признаков для распознавания объектов по дальностным портретам в импульсной лазерной локации

Современные средства формирования и регистрации излучения лазерных локационных систем дают возможность получения информации о характеристиках поверхностей объектов, которая используется для их распознавания [1 –7]. Локация объектов в оптическом диапазоне длин волн для реализации распознавания оказывается предпочтительнее использования для этой цели радиодиапазона благодаря лучшим энергетическим характеристикам оптических приемопередающих средств, а также меньшей изменчивости локационных сигналов при изменении пространственной ориентации объектов.

В ряде исследований продемонстрировано распознавание объектов, при локации которых разрешаются отдельные части их поверхности [3, 4], а также объектов, чьи размеры не превышают ширины зондирующего лазерного пучка в их окрестностях [2, 6–8]. Локационные системы первого типа предназначены для зондирования элементов сцен, расположенных на небольшом расстоянии. Информация об объекте представляется в них в виде трехмерного облака точек, описывающих поверхность, рассеявшую зондирующее излучение. В локационных системах второго типа распознавание выполняется в результате анализа амплитудно-временных характеристик сигналов, получаемых на выходе фотоприёмного устройства при облучении объекта короткими лазерными импульсами. Эти сигналы часто называют дальностными портретами (ДП) объектов. Менее жесткие требования к расходимости и точности наведения пучка излучения делают возможным применение таких систем при распознавании удаленных объектов. Кроме того, инвариант формы регистрируемых сигналов к изменению расстояния до объекта позволяет использовать более простые алгоритмы, чем те, которые применяют для обработки изображений и трехмерных облаков точек.

Функциональная схема лазерной локационной системы, реализующей распознавание объектов по ДП, представлена на рис. 1. Регистрируемое на выходе оптической системы приёмного канала лазерное излучение преобразуется в электрический сигнал, который подвергается квантованию и дискретизации. Дискриминатор компенсирует случайный сдвиг этого сигнала относительно начала интервала наблюдения.

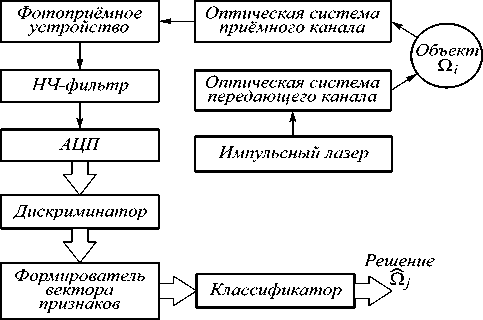
Рис. 1. Функциональная схема лазерной локационной системы, выполняющей анализ дальностных портретов

В блоке формирователя вектора признаков к полученной последовательности амплитудновременных отсчётов ДП применяется одно из известных преобразований [7–9] для формирования инварианта к условиям локации объекта и уменьшения размерности вектора признаков. Отсчёты, полученные в результате этого преобразования, передаются на вход классификатора, формирующего решение о принадлежности наблюдаемого объекта одному из известных классов.

Так как не все отсчеты, полученные в результате преобразования, содержат релевантную задаче распознавания информацию, при формировании векторов признаков целесообразно исключать малоинформативные компоненты, чтобы снизить размерность пространства признаков. Такую процедуру называют редукцией пространства признаков. Снижение размерности пространства признаков позволяет применить более простой классификатор и уменьшить вычислительные затраты на его обучение. С другой стороны, желательно изначально формировать пространство признаков так, чтобы векторы признаков содержали только наиболее информативные компоненты.

Хотя в настоящее время известен ряд методов синтеза векторов информативных признаков ДП [7– 11], проблема их эффективного формирования остается недостаточно исследованной и представляет интерес для анализа [12– 14].

1.    Формирование совокупности информативных признаков дальностных портретов

Один из наиболее известных методов формирования векторов признаков ДП – сигнатурный метод. Этот метод применен в [7, 10, 11] для формирования векторов признаков, инвариантных к изменению положения импульсных сигналов на оси времени. В [7] в качестве признаков использованы отношения величин экстремумов и отношения временных интервалов между ними. Полученные в результате применения этого метода векторы информативных признаков имеют малую размерность, что на практике позволяет отказаться от использования процедуры редукции пространства признаков. Очевидным недостатком этого метода является то, что при малом числе экстремумов теряется часть информации, которая может быть использована при распознавании объекта. Так, ДП объектов с простыми каноническими поверхностями, как правило, имеют один экстремум, что принципиально не позволяет различать их с использованием сигнатурного метода анализа [7].

В ряде работ [8, 9, 15, 16] предлагается к полученным отсчетам сигнала применять одно из известных интегральных преобразований [17–19]. Элементы полученного множества отсчетов S используются для формирования векторов признаков. Не все сформированные отсчеты оказываются информативными, поэтому используется только часть компонент множе- ства отсчетов S. Множество Sk ⊂ S содержит компоненты вектора информативных признаков, которые передаются в классификатор. Состав Sk определяется на основании оценки, называемой мерой информативности ϕ. Выражение для расчёта величины этой меры определяется как видом многомерного распределения векторов признаков обучающей выборки, так и типом используемого классификатора [20]. Схема алгоритма формирования пространства признаков представлена на рис. 2.

Множество информативных признаков мощности n выбирается на основании сравнения значений мер информативности ϕ q , рассчитываемых для каждого сочетания признаков S q , q = 1, 2,…, Q . При общем числе признаков N требуется рассмотреть Q - C N их сочетаний.

Частным случаем формирования пространства признаков на основании меры информативности является сравнительный анализ значений меры Фишера [21], которая используется в качестве меры информативности. При этом расчет меры Фишера ϕ ^f выполняется для каждого из N доступных признаков:

L

£ П ( ц ^f — ц ^f ) 2

Ф ^f - ^----------, f - 1,2,..., N ,              (1)

£ n ( ^{с f} )²

l -1

где l – номер объекта; n l – число реализаций ДП для объекта с номером l ; L – общее число различаемых объектов; ц if - математическое ожидание значений A l ^f (см. рис. 2) признака с номером f , рассчитанное для множества ДП l -го объекта; ц ^f - математическое ожидание значения признака с номером f , рассчитанное для всех ДП; ( с if )² - дисперсия значения признака с номером f для l -го объекта.

Интегральная оценка информативности множества отсчётов Sq определяется выражением ф= = £ фf, q -1,2,..., Q.

f e S q

Наилучшему пространству признаков соответствует множество отсчетов S k , которое имеет наибольшее значение интегральной меры Фишера [21]:

фbe£S1 - тах(ф^), q -1,2,...,Q, q                                                  (2)

Ф ! =Ф ^et, .

Так как значения меры Фишера рассчитываются для каждого признака, множество Sk следует сформировать из признаков, обладающих наибольшими значениями этой меры. В результате удается ограничить число рассматриваемых вариантов сочетаний признаков. Как правило, число компонент n, включаемых в Sk, определяется числом признаков с такими значениями меры Фишера, которые многократно превышают значения этой меры для остальных признаков. Показано, что такой метод применим в условиях распозна- вания лоцируемых объектов, ориентация которых известна [15]. Она задаётся азимутом α и углом места β, определяющими положение вектора наблюдения объекта относительно его строительной оси (рис. 2).

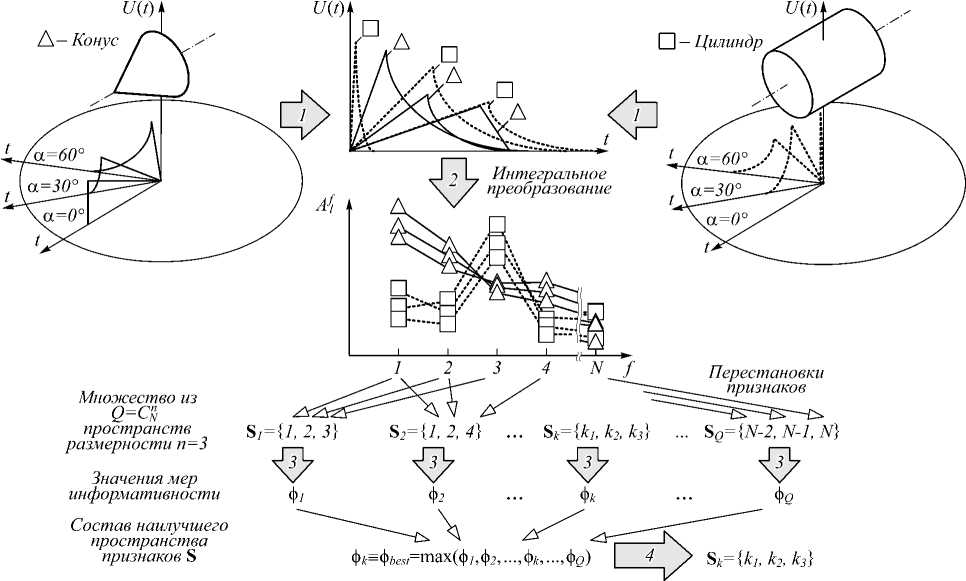
Рис. 2. Алгоритм формирования пространства признаков путём сравнения величин меры информативности – фигурными стрелками указаны выполняемые процедуры (1 – формирование множества дальностных портретов распознаваемых объектов путём математического моделирования или прямых измерений; 2 – интегральные преобразования отсчётов;

3 – расчёт величин меры информативности различных сочетаний признаков; 4 – выбор наилучшего сочетания признаков),

стрелками указаны реализуемые перестановки признаков

Если при оценке величин углов α и β имеют место значительные погрешности, то распределения признаков отличаются от нормальных, свойственных результатам, получаемым при малых погрешностях оценок этих углов [22]. Такая ситуация имеет место для большинства техногенных объектов при немногих исключениях. Из [23, 24] следует, что если одна из компонент векторов признаков имеет распределение, отличное от нормального, то это может помешать достижению наилучшего результата при формировании пространства признаков на основании меры Фишера. Пример элементарного множества векторов признаков, для которого невозможно корректно выбрать информативный признак, используя меру Фишера, представлен на рис. 3. Видно, что распознавание достижимо при использовании единственного признака – величины компоненты f 1 . Однако значение математического ожидания μ 1 , рассчитанное для множества всех векторов признаков, совпадает со значениями математических ожиданий ц 1 и ц 2 этого признака, рассчитанными для множеств векторов признаков, принадлежащих отдельным объектам. Из-за этого числитель выражения (1) стремится к нулю, сигнализируя о малой информативности признака f 1 .

Для формирования пространства информативных признаков при значительных погрешностях опреде- ления положения вектора наблюдения объекта в [8] предложен метод, основанный на отборе низкочастотных компонент амплитудного спектра ДП, используемых в качестве признаков, и максимизации метрик, определяемых между парами векторов этих признаков. Векторы признаков, полученные этим методом, инвариантны к временным сдвигам ДП: амплитудный спектр функции инвариантен к её сдвигу по оси абсцисс.

Информативность пространства признаков в [8] предложено оценивать на основании меры

ММ

Р q = i =1 j=1

Ё ( w f ( x{ ^- x j ))² f = 2 ___________________

I x i I • | x j I ’

где w ^f – весовой коэффициент, соответствующий f -м компонентам M векторов признаков; | x i |, | x j | – модули i -го и j -го векторов признаков; x i ^f – значения f -го компонента вектора признаков i -го ДП.

В [8] этот критерий был использован для определения минимальной размерности пространства признаков n, при которой обеспечивается как распознавание тестовых объектов, так и определение углов α и β. Отсчет спектра, соответствующий нулевой гармонике, исключался из рассмотрения в связи со сложно- стью получения несмещенной оценки его величины. Заметим, что реализация (3) подразумевает значительные вычислительные затраты, а использование отсчетов амплитудного спектра приводит к потере информации о временном положении характерных точек ДП. Для сохранения этой информации в [16] в качестве признаков использованы амплитудные компоненты комплексного вейвлет-преобразования, значения которых инвариантны к временным сдвигам входных сигналов в некоторых пределах. Значения пределов, в которых реализуется инвариант к сдвигу, определяются протяженностью используемых базисных функций. Хотя при таком преобразовании часть информации о временном положении характерных точек ДП также теряется, инвариант коэффициентов приводит к уменьшению прецессии векторов признаков, вызываемых временными сдвигами сигналов.

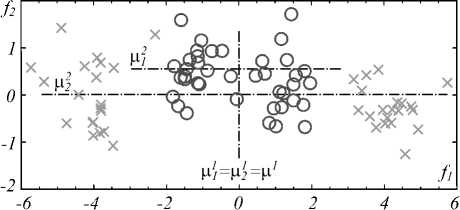
Рис. 3. Иллюстрация линейно неразделимых множеств векторов признаков (символами обозначены координаты их концов в двухмерном пространстве: (×) – векторы объекта 1, (○) – векторы объекта 2)

Вместе с тем низкочастотные составляющие амплитудных спектров ДП объектов однотипных конструкций могут различаться несущественно, что приводит к необходимости включения в состав S k высокочастотных компонент спектра. Отметим, что в отличие от других рассматриваемых методов в [8] эти компоненты включаются в состав пространства признаков в последнюю очередь.

2.    Формирование пространства признаков путем анализа минимальной метрики между векторами

В [9] множество признаков S k предложено определять путем сравнительного анализа метрик, вычисляемых между парами векторов признаков. Наилучшим для проведения распознавания предложено признавать пространство признаков, в котором достигается максимальное значение минимальной евклидовой метрики ρ^min между реализациями векторов признаков разных объектов.

В процессе поиска для всех множеств S q , q = 1,..., Q , определяются метрики p min . Затем устанавливается номер k того множества S k , для которого значение минимальной метрики пространства признаков оказывается максимальным (см. рис. 2). По сути, речь идет об определении той системы признаков, в которой наихудшая ситуация будет лучше всего различима.

Значения метрик pqi;m,j между i-м вектором признаков объекта с номером l и j-м вектором признаков объекта с номером m рассчитываются в пространстве признаков, заданном множеством Sq pq,i;m,j - E (xL- xfm,j)2, feSq где xlf,i и xmf , j – значения компонент векторов признаков объектов; Ml и Mm – числа реализаций ДП, принадлежащих l-му и m-му объектам; L – число распознаваемых объектов. При этом i -1,2,...,Mt; l - 1,2,...,L -1;

j - 1, 2,..., M m ; m - 1 + 1, l + 2,..., L .

Минимальная метрика pmin, характеризующая информативность пространства признаков, определяется в соответствии с выражением pmin - min(p lfm-j).                                    (4)

l , i , m , j

Общее число сравниваемых метрик p qi ^{; m , j} равно z :

L -1 L

Z - E l E ( M l • M m ) l -1 \ m - 1 +1

Метрика pmin со значением pmn- max(pmi"), q -1,2,...,Q, q                                                  (5)

Pmin     min k — p best, максимальным среди Q минимальных метрик, найденных согласно (4), соответствует множеству отсчетов Sk, задающему наилучшее в оговоренном выше смысле пространство признаков.

При выполнении такого анализа при всех возможных размерностях пространства признаков n = 1, 2,…, N число подлежащих анализу пространств информативных признаков составит 2 ^N . Как правило, множество признаков, найденное для размерности n , будет содержать компоненты множества информативных признаков, найденного для пространства размерности ( n - 1). Это обстоятельство позволяет уменьшить число анализируемых пространств признаков за счет применения эвристического алгоритма [25], реализующего поочередное добавление и удаление компонент множеств признаков S 1 , S 2 ,…, S N – n +1 . Вопрос о корректности сравнения информативности пространств признаков, полученных в результате такого анализа для различных значений размерности n , остается открытым из-за проблемы нормировки метрик в этих пространствах.

3.    Формирование пространства признаков путем анализа сумм метрик между векторами признаков

В тех случаях, когда распознаваемые объекты характеризуются схожими ДП, весьма вероятны пересечения множеств векторов признаков. При этом от- личия между ближайшими векторами признаков могут быть настолько малыми, что объекты окажутся неразличимыми. Такие пересечения множеств векторов признаков возникают и при распознавании объектов с простейшими поверхностями: регистрируемые при некоторых углах α и β ДП конуса и сферы с одинаковыми габаритными размерами оказываются схожими.

Пример элементарного множества векторов признаков, анализ которого затруднен наличием пересечений, представлен на рис. 4.

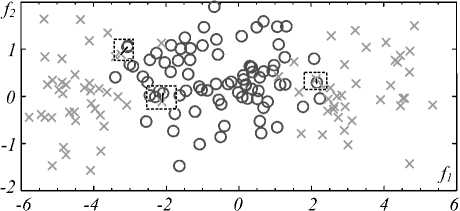
Рис. 4. Пример, иллюстрирующий взаимное расположение частично пересекающихся множеств векторов признаков ДП (символами обозначены координаты их концов в двухмерном пространстве: (×) – векторы ДП объекта 1, (○) – векторы ДП объекта 2)

Очевидно, что использование признака f 1 для решения задачи распознавания предпочтительно по отношению к использованию признака f 2 . Однако значения р min , получаемые при использовании того или иного признака, близки к нулю, что препятствует использованию р min в качестве меры информативности.

Соответствующие векторы признаков характеризуются такими же значениями математических ожиданий величин их компонент, как и векторы, образующие множества, представленные на рис. 3. В этом случае ни метод [9], ни метод [21] не гарантируют формирования пространства информативных признаков малой размерности, что затрудняет устойчивое распознавание объектов. Заметим, что уменьшение длительности зондирующих импульсов нередко не позволяет устранить пересечения множеств векторов признаков.

В рассматриваемом случае целесообразно снизить влияние метрик с малыми значениями на результат определения множества признаков S k . Для этого предложено определять максимальное значение среди сумм метрик, формируемых для всех пространств признаков заданной размерности n :

L-1 L Ml Mm р f=EEEZ р м; m ,j. (6)

l =1 m = l +1 i =1 j =1

Следует найти метрику рf , имеющую значение рL = тах(рf), q = 1,2,..., Q, q                                                  (7)

р ^f =р IL .

В (7), как и в (2) и (5), k является номером искомого сочетания признаков S k .

Поскольку мера (6), в отличие от меры (3), не учитывает значений метрик между векторами признаков одного и того же объекта, состав множества S k будет зависеть от отличий ДП различных объектов и практически не будет зависеть от их отличий для разных наблюдаемых ракурсов одного и того же объекта.

Применение метода максимизации суммы метрик возможно тогда, когда множества векторов признаков имеют пересечения, а компоненты этих векторов характеризуются близкими значениями математических ожиданий, что выгодно отличает предложенный метод от ранее известных [9, 21].

• 4.    Сравнительный анализ результатов применения различных методов формирования пространств признаков

Для сравнения результатов применения изложенных методов формирования пространств признаков были оценены вероятности ошибок распознавания тестовых объектов нейросетевым классификатором.

Реализации сигнала сформированы для тестовых объектов с поверхностями, описываемыми каноническими уравнениями сферы, конуса и цилиндра. Диаметры сферы и оснований конуса и цилиндра приняты равными 1 м, а высоты конуса и цилиндра – 3 м. Полагалось, что угол места β вектора наблюдения неизменен и составляет 0°, а азимут α находится в пределах от 0 до 90°. Характер рассеяния излучения поверхностью объекта считался диффузным, а шум – аддитивным. Длительность зондирующих импульсов лазерного излучения принята равной 5 нс. Такая длительность импульсов характерна для твердотельных лазеров и часто реализуется лазерами, применяемыми в системах распознавания [1, 6, 7]. Число сформированных реализаций ДП превышает 2000, что достаточно для получения достоверного результата [8].

Для формирования пространств признаков использовались:

• -    отсчеты амплитудного спектра [17];

• -    коэффициенты вейвлет-преобразования [18];

• -    амплитудные компоненты комплексного вейвлет-преобразования [15, 19].

Как известно, вейвлет-преобразование состоит в разложении одномерного сигнала по базису, сконструированному из порождающей функции, называемой материнским вейвлетом [18]. В [26–28] предложены методы выбора его типа для заданного множества сигналов. Материнский вейвлет выбран на основании принципа минимизации ошибки реконструкции сигналов [28] – в диапазоне азимутов 0,2,…,90° наименьшую ошибку восстановления сигнала позволило получить применение симметричного вейвлета 2-го порядка.

Применение амплитудных компонент комплексного вейвлет-преобразования позволило реализовать частичный инвариант значений признаков к сдвигам ДП по временной оси. Это преобразование предпо- чтительно использовать в тех случаях, когда величина погрешности компенсации временного сдвига превышает интервал дискретизации сигнала.

Полученные тремя указанными способами отсчеты преобразований использовались для формирования пространства признаков. Для каждого сочетания метода преобразования и способа оценки информативности полученных отсчетов проводилось обучение нейросетевых классификаторов. Обучаемые классификаторы имели схожие топологии нейронных сетей: число слоёв – 3, числа нейронов в слоях – 16, 8 и 3. Число входов каждого классификатора принималось равным размерности пространства признаков n . Минимальная величина n принята равной 6 – при меньшем её значении сложно судить о соответствии результата обратного преобразования исходному сигналу. Схема алгоритма оценивания качества распознавания представлена на рис. 5.

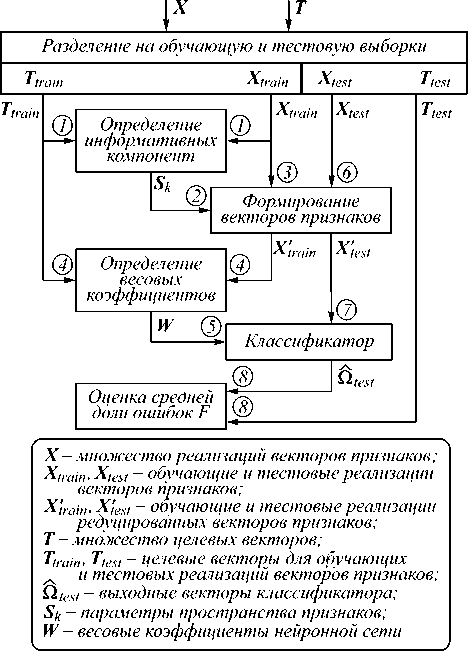
Рис. 5. Алгоритм оценивания качества распознавания (цифрами обозначен порядок выполнения процедур)

Из-за ограниченного числа примеров для тестирования обученных нейронных сетей применён метод перекрёстной проверки [29]. Этот метод позволяет оценить обобщающую способность системы распознавания на множестве реализаций векторов признаков ограниченного размера. В ходе перекрёстной проверки множество реализаций векторов признаков X было разделено на 3 выборки, а результирующая вероятность ошибки рассчитывалась как среднее значение вероятностей ошибки для всех тестовых выборок.

Хотя существует ряд критериев, используемых для оценки качества распознавания [30–33], наиболее часто для сравнения результатов функционирования нейросетевых классификаторов применяют величину доли правильных ответов D = d / M , где M – число реализаций сигналов в тестовой выборке; d – число правильных ответов.

Для сравнения качества распознавания авторами был использован анализ долей ошибочных решений F = 1 – D , полученных при использовании разных алгоритмов выбора информативных признаков. Для каждого объекта сформировано одинаковое число реализаций сигналов.

На рис. 6 представлены зависимости доли ошибочных решений F от числа n использованных информативных признаков. Видно, что среднее значение F зависит как от используемого интегрального преобразования ДП U ( t ), так и от уровня аддитивного шума σ n .

В целом, применение преобразования Фурье для формирования пространства признаков приводит к большей вероятности ошибок распознавания, чем применение различных типов вейвлет-преобразований.

Заметим, что при малом уровне шума (σ n = 0,008 В при амплитуде ДП 0,16 В) применение вейвлет-преобразования позволяет получить несколько лучшие вероятностные характеристики распознавания, чем применение преобразования Фурье и комплексного вейвлет-преобразования.

Метод максимизации суммы метрик позволил найти пространство признаков, характеризующееся наименьшими значениями доли ошибок даже в том случае, когда число анализируемых ДП возрастает. Такая ситуация имеет место при увеличении погрешности оценки углов α и β, задающих вектор наблюдения. При этом размерность n пространства признаков оказывается меньше их общего числа N . Другие исследуемые методы не гарантируют получения значения n <  N – найденная величина n может стремиться к N .

Заключение

Анализ известных методов формирования пространств информативных признаков дальностных портретов показывает, что в ряде случаев при редукции пространства признаков вместе с неинформативными компонентами из состава вектора признаков исключаются компоненты, содержащие информацию, релевантную задаче распознавания. Выбор конкретного метода определяется погрешностью оценки положения объекта относительно локационной системы.

Показано, что выбор интегрального преобразования, используемого при синтезе пространства признаков, существенно влияет на величину достижимой вероятности ошибки распознавания. Продемонстрирована нецелесообразность применения метода мак- симизации минимальной метрики, когда распознаваемые объекты имеют большое число схожих ДП.

Установлено, что применение метода максимизации суммы метрик предпочтительно, поскольку веро- ятностные характеристики распознавания, достижи мые при его использовании, оказываются не хуже по лученных при использовании метода Фишера, а в ря де случаев заметно превосходят их.

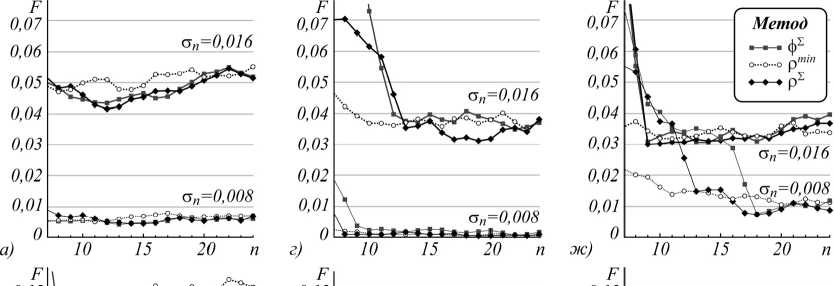
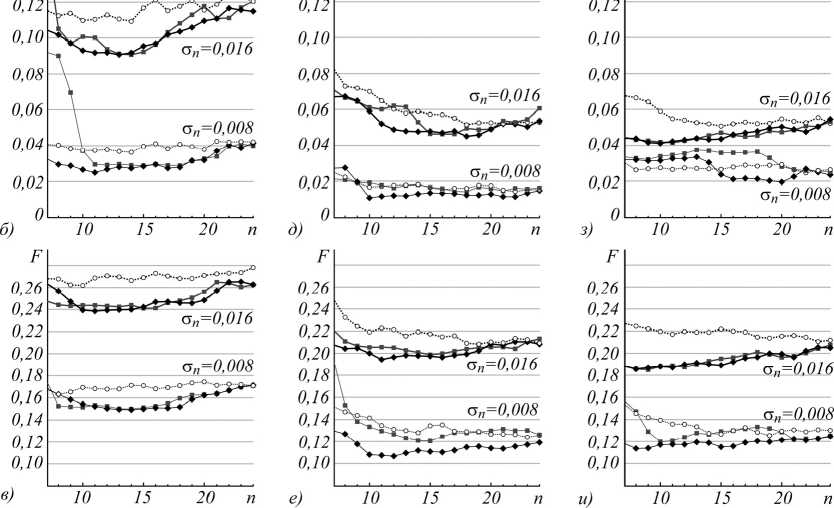
Рис. 6. Зависимости долей ошибок распознавания F от числа выбранных признаков n для отсчётов амплитудного спектра (а – в), коэффициентов вейвлет-преобразования (г – е), коэффициентов КВП (ж – и), полученные при использовании различных методов формирования пространств признаков.

Верхний ряд графиков (а, г, ж) соответствует диапазону азимутов α = 0°, 1°,…, 30°, средний (б, д, з) – диапазону азимутов α = 0°, 2°,…, 60°, нижний ряд (в, е, и) – диапазону азимутов α=0°, 2°,…, 90°