Методы хаотической динамики в задаче анализа временных рядов Вольфа
Автор: Бондаренко Михаил Анатольевич
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Кибернетика, системный анализ, приложения
Статья в выпуске: 5 (31), 2010 года.
Бесплатный доступ
Представлены результаты компьютерного исследования временного ряда, составленного из чисел Вольфа. В соответствии с подходом, основанным на теореме Такенса, решалась задача восстановления размерности аттрактора динамической системы, описывающей динамику Солнца. Показано, что за последние 3 000 лет принципиальных изменений в эволюции Солнца не произошло.
Теорема такенса, реконструкция аттрактора, числа вольфа
Короткий адрес: https://sciup.org/148176310
IDR: 148176310 | УДК: 517.9
Methods for chaotic dynamics in the problem of analysis of Wolfer’s time series
The results of computer studies of time series composed of the Wolfer's numbers are presented in the article. In accordance with the approach based on Takens's theorem, the author solves the problem of reconstructing dimension of attractor of a dynamical system describing the dynamics of the Sun. It is shown that for the last 3 000 years, fundamental changes in the evolution of the Sun have not happened.
Текст научной статьи Методы хаотической динамики в задаче анализа временных рядов Вольфа
Математические модели, содержащие три и более обыкновенных дифференциальных уравнений (ОДУ), способны демонстрировать хаотические режимы колебаний, которые на первый взгляд имеют вид случайных процессов. Переход в фазовое пространство позволяет получать наглядную информацию об особенностях сложной динамики соответствующих систем, прежде всего о геометрии предельных множеств фазовых траекторий, которые соответствуют установившимся режимам [1].
В последнее время это свойство хаотичности нелинейных диссипативных динамических систем активно используется для анализа временных рядов. Основным моментом здесь является предположение о том, что данный временной ряд порожден некоторым функционалом от решения неизвестной нам динамической системы с аттрактором. Алгоритм Грассберга– Прокаччиа [2], используемый в данной статье, позволяет получить оценку для корреляционной размерности этого аттрактора. Она и является тем параметром, который характеризует качественное поведение траекторий такой динамической системы. В работе в качестве временного ряда автором были выбраны числа Вольфа, называемые также международными числами солнечных пятен, относительными числами солнечных пятен или цюрихскими числами.
Солнечные пятна – это темные области на Солнце, температура которых понижена примерно на 1 500 К по сравнению с окружающими участками фотосферы. Количество пятен на Солнце и связанное с ним число Вольфа – одни из главных показателей солнечной магнитной активности. Прямые наблюдения солнечных пятен доступны в течение последних четырех столетий (рис. 1), но более длительный временной ряд необходим, например, для выявления возможного воздействия Солнца на климат и для проверки моделей солнечного динамо.
В работе [3] приведены результаты реконструкции чисел Вольфа на период, охватывающий последние 11 400 лет. Эти результаты были получены на основании дендрохронологического анализа радиоуглеродной концентрации ископаемых останков растений. На основании объединенной физико-биологической модели была построена связь процессов набора определенной радиоуглеродной концентрации с числами Вольфа.
Количество
Рис. 1. Количество солнечных пятен в зависимости от года
Согласно полученной реконструкции, уровень солнечной активности за последние 70 лет является исключительным случаем. Предыдущий период столь же высокой активности произошел более 8 000 лет назад. Было подсчитано, что в течение последних 11 400 лет Солнце провело лишь порядка 10 % времени на столь же высоком уровне магнитной активности, и почти все предыдущие периоды такой активности были гораздо короче, чем нынешний эпизод.
Редкость текущего эпизода высокого среднего числа солнечных пятен может свидетельствовать о том, что Солнце внесло свой вклад в необычные климатические изменения в течение XX в. Но насколько значимы эти отклонения? Являются ли они некоторым сигналом того, что на Солнце происходят какие-то изменения в механизме термоядерного синтеза или же это простые временные флуктуации? Будем считать, что числа Вольфа порождены некоторой динамической системой, описывающей временную эволюцию Солнца.
Была поставлена следующая задача: сравнить размерность аттрактора Солнца за последние 130 лет с его глобальным поведением за 11 400 лет. Разные величины N с аттрактором размерности N будут говорить о том, что в последние 130 лет в механизме Солнца происходят качественные изменения.
Для решения этой задачи выбраны два временных ряда для чисел Вольфа:
– соответствующий 11 400 годам через промежуток 100 лет;
– соответствующий 130 годам через промежуток 1 год.
Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева
Для каждого из этих случаев определялась временная задержка τ (рис. 2–4). Необходимо, чтобы система достаточно долго находилась на аттракторе, но при этом слишком детальное описание ее движения приведет к определенным трудностям.
Числовым показателем количества пятен на Солнце является число Вольфа. Для данного дня это число определяется
W = k ( f + 10 g ), (1) где k – нормировочный коэффициент; f – количество наблюдаемых пятен; g – количество наблюдаемых групп пятен.
Для нахождения величины временной задержки τ на интервале 9400 г. до н. э. – 2000 г. н. э. с шагом 10 лет были использованы метод взаимной информации I (τ):
I (т) = - EE P (AB J) • log2 P(AiBi) , (2) Е Е j J " P(Ai)P(Bj) v ’ где P(∙) – вероятность соответствующего события, и метод автокорреляционной функции R(τ):
-
1 N 1
R ( т ) = ттЕ y (t ) y (t +т ). (3) N 1 t = 1
Анализ графика зависимости I (τ) и R (τ) от выбора временной задержки τ (рис. 2) показывает, что первый минимум встречается при τ = 5.
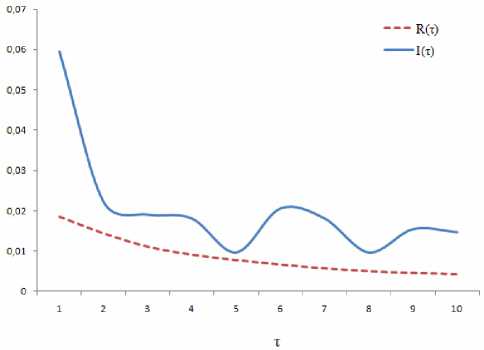
Рис. 2. График зависимости функции взаимной информации I (τ) и автокорреляционной функции R (τ) от временной задержки τ для интервала 9400 г. до н. э. – 2000 г. н. э. с шагом 10 лет
Для определения размерности пространства вложения был использован метод Грассберга–Прокаччиа [2]. На графике d ( m ), представленном на рис. 3, насыщение наступает при m = 3, при этом d = 1,81. Исходя из этого можно сделать вывод, что размерность пространства вложения составит d ≥ 2 [ d (3)] + 1 = 3.
Для нахождения временной задержки τ на интервале 1870–2000 гг. с шагом 1 год были использованы методы взаимной информации I (τ) (2) и автокорреляционной функции R (τ) (3) (рис. 4). Очевидно, что в качестве временной задержки в этом случае можно использовать τ = 3 или τ = 4.
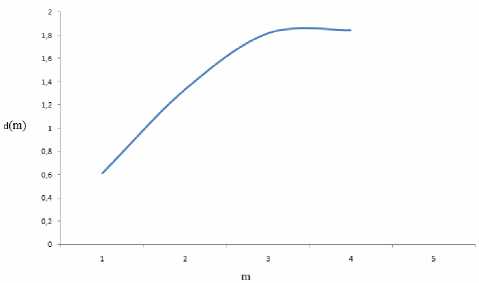
Рис. 3. График зависимости коэффициента корреляционной размерности d от размерности m для интервала 9400 г. до н. э. – 2000 г. н. э. с шагом 10 лет
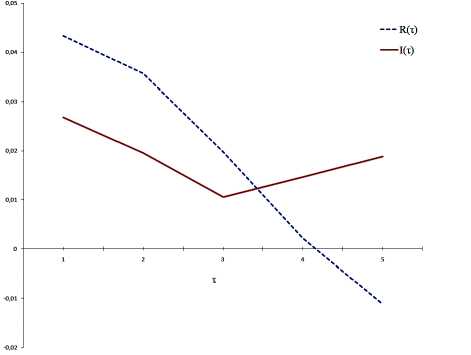
Рис. 4. График зависимости автокорреляционной функции R (τ) и функции взаимной информации I (τ) от временной задержки τ для интервала 1870–2000 гг. с шагом 1 год
Вычислим размерность пространства вложения методом Грассберга–Прокаччиа [2] для временного интервала 1870–2000 гг. (рис. 5). Можно отметить, что d ( m ) также достигает своего насыщения при размерности 1,81. В этом случае имеем следующую оценку размерности пространства вложения: d ≥ 2 [1,81] + 1 = 3.
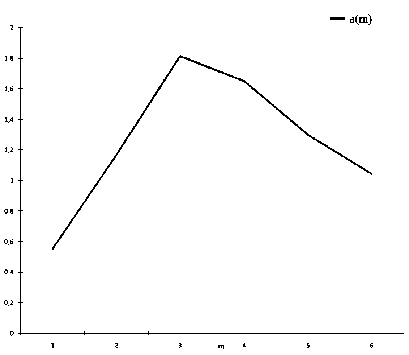
Рис. 5. График зависимости коэффициента корреляционной размерности d от размерности m для временного ряда, составленного из чисел Вольфа, для интервала 1870–2000 гг.
