Методы и алгоритмы учета конструкции обмоток асинхронных машин в системах частотного электропривода

Постановка задачи

Асинхронный электропривод – это довольно сложный объект для регулирования, поскольку описывается системой нелинейных дифференциальных уравнений. Один из подходов к решению этой проблемы состоял в том, что исходная трехфазная система электрической и магнитной цепей асинхронной машины (АМ) преобразовывалась в двухфазную систему с ортогональными пространственными осями координат. Для таких пространственных систем давно был разработан метод анализа, метод двух реакций (André Blondel, 1899), основанный на преобразовании векторов на комплексной плоскости (ПВК). В XX веке преобразования векторов методом двух реакций применяли многие ученые (Robert H. Park, 1929; А.А. Горев, 1935; Edith Clark, 1943). Однако эти преобразования основаны на условии синусоидальности распределения магнитной индукции в воздушном зазоре АМ. Считается, что это условие всегда выполняется в АМ независимо от того, какой тип схемы обмоток используется [1–6]. Аналогичной позиции придерживаются и зарубежные исследователи [7–12]. Поскольку обмотки АМ размещают по пазам магнитных систем статора и ротора, распределение магнитной индукции в воздушном зазоре машины оказывается не всегда синусоидальным, что известно из курса электрических машин [2].

Авторы провели анализ распределения магнитной индукции в зазоре машины для некоторых распространенных схем соединения секций обмоток АМ, используя метод зубцовых контуров [13]. Особенность этого метода, примененная авторами, состоит в том, что расчеты проводились не с физическими величинами магнитных потоков, а с относительными значениями этих потоков, что позволило уменьшить зависимость расчетов от конструкции зубцового пространства.

В зарубежной научной литературе эквивалентом методу зубцовых контуров служит метод обмоточных функций [9]. Им выполнены исследования моделей трехфазной АМ с обозначением зависимости взаимных индуктивных связей обмоток от положения ротора, но работы не доведены до численных расчетов для конкретных типов обмоток машины [8, 10–13]. В ряде работ исследуют изменения параметров модели АМ в результате эксцентриситета ротора относительно статора, а также в результате дефектов обмоток ротора [12].

Однако исходной моделью для анализа при этом остается та же модель идеализированной АМ.

Такое положение, по нашему мнению, можно объяснить лишь огромным уважением исследователей к работам основоположников метода двух реакций, проверенного многолетними применениями в электрических машинах. Стремительное развитие силовой электроники, компьютерной техники и технологий заставляет относиться критически к основам методов анализа, разработанным на другой технической базе.

Моделирование пуска асинхронного двигателя в среде MATLAB показало, что даже незначительное отклонение распределения магнитной индукции от синусоидальной формы оказывает заметное влияние на токи, на магнитные потоки и на электромеханические процессы [14, 16, 18].

равна произведению числа витков) w (n) на величину тока зубцовой катушки i _s : F _{( n )} = w _{( n )} ⋅ i _S . Относительная величина МДС зубца рассчитывается *

аналогично – F ₍ ^* _{т )} = F _{( n )} / F _{( N )max} = w _{( n )} / w _{( N )} . Для линейной магнитной цепи машины имеем соотношения

Ψ ∗ ( n ) =Ψ ( n ) / Ψ ( N )max =

Усовершенствованный метод зубцовых

контуров для расчета взаимных индуктивных связей между обмотками асинхронной машины

Работа асинхронной машины (АМ) основана на взаимодействии магнитных потоков. Поэтому необходимо точно знать распределение магнитных потоков в АМ. Магнитное потокосцепление для

отдельного n -го зубца ( n -й зубцовой катушки, n -го зубцового контура) рассчитывалось по выражениям

n + 1

Ψ ( n ) = w ( n ) ∫ B ( n )

n

n + 1 H

⋅∆ S ( n ) = w ( n ) ∫ [ ^{( n )}] ∆ S ( n ) ≅ _n µ ₀

≅ w ( n )

ⁿ ∫ ^{+ 1} [ ^{( F ( n ) )} ] ∆ S ( n ) n 2 δ ( n ) µ 0

= w ( n )

n + 1

∫ ^[

n

( w ( n ) ⋅ i S ) 2 δ ( n ) µ 0

] Δ S ( n ) =

w (² n ) ⋅ i S 2 δ ( n ) µ 0

2          ( n )

Δ S ( n ) = w ( n ) [_{2 δ ( n ) µ 0}

] i _S .

Здесь обозначены: Ψ ( _n ) – потокосцепление n -го зубцового контура; w ( n ) – число витков зубцового контура (зубцовой катушки); B ( n ) – усредненное значение магнитной индукции в воздушном зазоре для n -го зубца; Δ S ( n ) – площадь зубца, пронизываемая перпендикулярно вектором магнитной индукции; H ( n ) – усредненное значение напряженности магнитного поля по площади зубца; δ ( _n ) – усредненная величина воздушного зазора в области зубца (учтена длина двух воздушных зазоров вдоль силовой линии магнитного поля машины); µ ₀ = 4 π ⋅ 10 ^{- 7} [Гн/м] – магнитная проницаемость

воздуха; F ( _n ) – магнитодвижущая сила (МДС) зубцового контура (зубцовой катушки); i _S – ток зубцовой катушки, в данном случае обмотки статора.

Отношение потокосцепления данного n -го зубца Ψ ( n ) к максимальному значению этого потокосцепления для одного из зубцов Ψ ( n )max в полюсной зоне обмотки дает относительную величину потокосцепления n -го зубца Ψ _{( n )} / Ψ _{( N )max} = Ψ^∗ _{( n )} . Маг-

нитодвижущая сила (МДС) зубцовой катушки F ( n )

2     ^{Δ S} ( n )          2     ^{Δ S} ( n )

= w ₍ ² _{n )} [         ] i _S /{ w ₍ ² _{N )} [         ] i _S } =

2 δ ( n ) µ 0              2 δ ( n ) µ 0

= w (² n ) / w (² N ) = [ F ( n ) / F ( N )max ] ² = F ( n ²) .          (2)

В полученных выражениях потокосцепление Ψ ( n ) зубца пропорционально квадрату МДС. Изменение числа витков обмотки, относящееся к данному зубцу, связано с размещением реальной фазной обмотки секциями по пазам машины [2].

При реальных магнитных свойствах материалов статора и ротора разница в величине падения магнитного напряжения на воздушном зазоре для разных зубцов в зоне одной и той же секции обмотки не превышает нескольких процентов [2]. В случае линейной магнитной цепи машины отношение чисел витков по зубцам может быть заменено отношением числа секций обмотки, которое приходится на пространство данного зубца. Относительная величина магнитного потокосцепления Ψ ^*( _n ) любого зубца пропорциональна квадрату числа секций обмотки, приходящихся на данный зубец, и может быть представлена как функция угла смещения θ вдоль воздушного зазора машины – Ψ^∗ _{( n )} =Ψ^∗ ( n ) =Ψ^∗ ( θ ^* ) или аппроксимирована непрерывными функциями от непрерывного угла смещения, Ψ^∗ ( θ ^*) ⇒Ψ^∗ ( θ ) .

Усредненное значение магнитной индукции зубца В ( _n ) распределено вдоль воздушного зазора машины пропорционально МДС зубца F ( n ) :

B ( n ) = H ( n ) / µ 0 ≅ F ( n ) /(2 δ ( n ) µ 0 ) =

= w ( n ) ⋅ [ i S /(2 δ ( n ) µ 0 )].                           (3)

Отношение величины магнитной индукции зубца В ( n ) к ее наибольшей величине В ( n )max (относительная величина магнитной индукции В^* ( n ) ) в зоне полюса обмотки зависит только от распределения МДС:

*

B ( n ) = B ( n ) / B ( N )max = w ( n ) / w ( N )max =

*

= F ( n ) / F ( N )max = F ( n ) .                         (4)

Если суммировать относительные потокосцепления Ψ ^*( n ) для всех зубцов на пространстве одного полюсного деления обмотки, то получим относительную величину потокосцепления всей обмотки, например, обмотки фазы А статора:

τ

Ψ^∗ AA = ∑ Ψ^∗ ( n ) .                           (5)

n = 1

Сумма относительных потокосцеплений зуб-

Электромеханические системы цов Ψ ^*( n ) на пространстве полюсного деления τ, но уже со смещением на g зубцов даст относительную величину полного потокосцепления другой такой же по конструкции обмотки, но расположенной со смещением относительно первой обмотки на g зубцов (измерительная, пробная обмотка):

τ+ g

^Ψ∗ Aa ( g ) ⁼ ∑ ^Ψ∗ ( n ) ^{.                         (6)}

n = 1 + g

Отношение потокосцеплений Ψ^∗ _{Aa ( g )} / Ψ^∗ _AA = = KSAa ( g ) ⇒ KSAa ( ϑ ^*) есть коэффициент магнитной связи обмоток в АМ. Оно является основополагающим для изучения распределения магнитных потоков между обмотками АМ.

В частности, если относительно обмотки фазы А статора сместить измерительную обмотку на 2/3 полюсного деления τ (на 120° эл.), то измерительная обмотка займет положение обмотки фазы В статора:

τ+ 2 τ /3

^{Ψ ∗} AB ⁼ ∑ ^{Ψ ∗} ( n ) .                        (7)

n = 2 τ /3

Значение коэффициента магнитной связи обмоток фаз А и В статора:

Ψ^∗ AB / Ψ^∗ A = L AB / L AA = k AB = KSAa (120 ° ). (8)

В модели идеализированной АМ используется всегда одна и та же зависимость KSAa ( θ ^*) = cos( θ ^*) для любой конструкции обмоток.

Магнитный поток, прошедший через воздушный зазор машины, несомненно, достигнет магнитной цепи ротора и обмоток ротора. Следовательно, приведенные выше рассуждения справедливы и для потокосцеплений между обмоткой статора, создавшей магнитное поле машины, и обмотками ротора, т. е. относятся также к магнитным потокам взаимной индукции между обмотками статора и ротора.

Для модели идеализированной АМ относительная величина полного магнитного потокосцепления равна Ψ^∗ _{Aa ( g )} / Ψ^∗ _AA = KSAa ( g ) = cos( θ ) . Поэтому отношение KSAa ( ϑ ^*) к cos(θ) дает величину отличия распределения потокосцепления реальной машины относительно идеализированной АМ:

FKSR ( θ ^*) = KSAa ( θ ^*)/cos θ=

= KAa ( θ ^*) ⇒ KAa ( θ ) .                    (9)

Отношение KAa(θ) по (9) авторы предложили использовать в качестве поправочной функции к элементам матрицы взаимных индуктивностей между обмотками статора и ротора в системе уравнений идеализированной (АМ) [14–19]. Значение поправочной функции KAa(θ) для угла смещения θ = 120° дает величину поправочного коэффициента к элементам матрицы взаимных индуктивностей между обмотками статора, например, между обмотками фаз А и В статора:

KAa (θ AB ) = KAa (120°) = KSS .            (10)

Аналогичные выражения могут быть получены для взаимных индуктивностей между обмотками фаз фазного ротора. Более точный учет влияния вариантов конструкции короткозамкнутого ротора на модель АМ требует дополнительного рассмотрения и в данной работе не приводится.

Расчет поправочных функций и поправочных коэффициентов к модели идеализированной асинхронной машины Ниже как пример методики показаны расчеты поправочных функций и поправочных коэффициентов для машины с двухпериодной обмоткой статора и укороченным шагом при Z = 36 , y = 7, τ = 9, 2p = 4, выполненные в [14]. Раскладка секций обмотки по пазам взята из [2]. Обмотки ротора принимались приведенными к цепи статора и конструктивно подобными обмоткам фаз А, В и С статора.

Суммирование МДС зубцов в переделах одного полюсного деления обмотки фазы А статора оказывается эквивалентным (в условных единицах) полному магнитному потоку обмотки фазы А статора Ф ^* А (θ):

Ф ^* А (θ) = Σ Ф ^* ZА ( n Z ) .                         (11)

Потокосцепление самоиндукции обмотки фазы А статора распределено вдоль зазора пропорционально квадрату распределения МДС (индукции) по пазам[14]:

Ψ ^* ZА ( n Z ) = (Ф ^* ZА ( n Z )) ² .                       (12)

Суммирование потокосцеплений Ψ ^* ZА ( n Z ) всех зубцов полюсного деления (для пазов 1–9) дает относительную величину потокосцепления самоиндукции обмотки фазы А статора, равную +55 единиц: Ψ ^* А (θ = 0°) = ΣΨ ^* ZА ( n Z ) = 1…9) = +55.

В таблице приведены результаты расчетов по-токосцеплений Ψ ^* Aа (θ) на перемещаемую вдоль зазора машины измерительную обмотку, смещенную относительно обмотки фазы А статора на g пазов (на угол θ относительно обмотки фазы А статора) [14]. В таблице приведены также результаты расчетов поправочной функции KАа (θ).

Потокосцепления измерительной обмотки Ψ ^* _Aа (θ) и поправочная функция угла смещения относительно обмотки фазы А статора KАа (θ)

№ паза g	1	2	3	4	5	6	7	8	9	10
θ,° эл.	0	20	40	60	80	100	120	140	160	180
Ψ *Aа (θ), усл. ед.	+55	+51	+41	+26	+9	–9	–26	–41	–51	–55
KАа (θ)	1	0,987	0,973	0,945	0,943	0,943	0,946	0,973	0,987	1

Из таблицы видно, что смещение измерительной обмотки на угол θ = 120° относительно обмотки фазы А статора приведет к тому, что на пространство одного полюсного деления, где расположена обмотка фазы В статора, поступит только часть магнитного потока, равная Ψ ^* Aа (120°) = –26 единиц. Следовательно, коэффициент взаимной индуктивной связи обмотки фазы В статора с обмоткой фазы А статора составит k АВ = KSAa (120°) = Ψ ^* Aа (120°) /Ψ ^* Aа (0°) =–26 /+55=–0,4727.

По методу ПВК (для идеализированной модели АМ) коэффициент взаимной индуктивной связи обмоток фазы А и фазы В статора равен точно cos(120°) = –0,5.

Из таблицы видно, что магнитное потокосцепление фазы А статора реальной АМ (для рассматриваемого типа обмотки) проектируется на другие направления обмоток статора (и ротора) довольно близко к идеализированной АМ.

Поправочная функция KАа (θ) позволяет путем умножения на функцию cos(θ) получить элементы матрицы индуктивностей KSAa (θ) для реальной АМ:

[ L 12 K ] = L 1 m

cos( 9 ) ■ K 1 cos( 9- 120 ° ) ■ K 3 cos( 9 + 120 ° ) ■ K 2

cos( 9 + 120 ° ) ■ K 2 cos( 9 ) ■ K 1

cos( 9- 120 ° ) ■ K 3

cos( 9- 120 ° ) ■ K 3 cos( 9 + 120 ° ) ■ K 2

cos( 9 ) ■ K 1

Здесь обозначены: KАа (θ) = K 1, KАа (θ+120°) = K 2, KАа (θ – 120°) = K 3.

Значения поправочной функции KАа (θ) при θ = 2π/3 и при θ = 4π/3 дают поправочные коэффициенты KSS. Они учитываются в уточненной матрице индуктивностей и взаимных индуктивностей обмоток статора ( KSS = KAB = = KBA = KAC = = KCA = KBC = KCB = KAa (120°) = 0,946) в системе уравнений модели идеализированной АМ с целью приведения ее к матрице взаимных индуктивностей для реальной машины [14]:

1 + k_{1 a}   - 0,5 ' KAB - 0,5 ' KAC

^[ L K ^] = L 1 m

- 0,5 ' KBA   1 + k_{1 a}

- 0,5 ' KCA - 0,5 - KCB

- 0,5 " KBC 1 + k_to

[ L K ] = L m ([1] . k _to+ [ Kmss ■ KSS ]).

Для шаблонной обмотки вразвалку при Z = 24, p = 2, q = 4, τ = 12, y = 10 (1–11) поправочный коэффициент равен KSS = 0,889, а для двухслойной обмотки при Z = 24, 2 р = 4, q = 2 поправочный коэффициент равен KSS = 0,842. Расчеты для этих обмоток подтверждают выводы, полученные из вышеприведенного анализа магнитных потоков двухпериодной обмотки с укороченным шагом при Z = 36, y = 7, τ = 9, 2 p = 4. Последняя имеет наилучшее из анализированных обмоток распределение магнитной индукции, приближающееся к синусоидальному [14].

Поправочные коэффициенты к матрице взаимных индуктивностей между обмотками фазного ротора могут быть вычислены по той же методике, которая использована выше для обмоток статора. Для короткозамкнутого ротора можно предположить, что распределенные одновитковые короткозамкнутые обмотки ротора в результате приведения цепи ротора к цепи статора получат распределение магнитных потоков, подобное обмотке статора.

В [14] приведены также расчетные (относительные) значения для производной от потокосцепления обмотки фазы А статора по углу поворота ротора относительно статора d Ψ ^* Aa (θ) / d θ. Производная от взаимных индуктивностей между обмотками статора и ротора используется в уравнениях АМ для расчета момента вращения, например, в системе MATLAB/Simulink.

В модели идеализированной АМ производная от коэффициентов взаимных индуктивных связей меж- ду обмотками статора и ротора для любого типа обмоток одинакова - d^Aa (0) / d0 = sin(0).

Отношение KМAa (θ) = ( d Ψ ^* _Aa (θ) / d θ)) / sin(θ) предложено авторами в качестве поправочной функции к элементам матрицы производных от взаимных индуктивностей между обмотками статора и ротора в модели идеализированной АМ [14–19] (15):

^[ L 12 ^] = L 1 m d У

- sin( y ) ■ KM 1

- sin( 9- 120 ° ) ■ KM 3

- sin( 9 + 120 ° ) ■ KM 2

- sin( 9 + 120 ° ) ■ KM 2

- sin( 9 ) ■ KM 1

- sin( 9- 120 ° ) ■ KM 3

- sin( 9- 120 ° ) ■ KM 3

- sin( 9 + 120 ° ) ■ KM 2

- sin( 9 ) ■ KM 1

В (15) обозначено: KМАа (θ) = KМ 1, KМАа (θ+120°) = KМ 2, KМАа (θ–120°) = KМ 3.

В системах частотного управления для расчета момента вращения АМ используются различные произведения ортогональных составляющих векторов токов и магнитных потоков двухфазной модели машины [1]. Учет конструкции обмоток в этом случае следует производить при преобразовании токов и напряжений трехфазной машины в эквивалентную двухфазную машину.

Как показало моделирование в системе MATLAB, даже небольшое уточнение коэффициентов связи обмоток оказывает заметное влияние на электромагнитные и электромеханические процессы в АМ [14, 18].

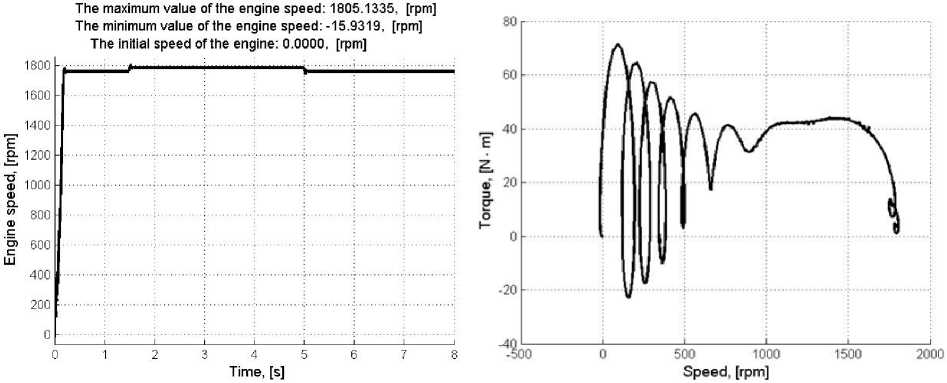
Рис. 1

Рис. 2

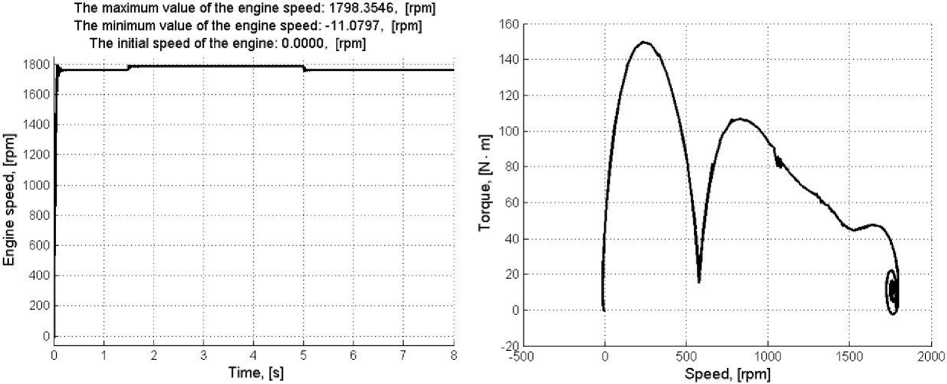
Рис. 3

Рис. 4

Н иже п р ив е дены нов ые резул ь та ты м одел ирования в среде MATLAB. На р и с . 1. показан график скорости, а на рис. 2 п оказ а на д ина миче с ка я ме х а н иче с ка я х а ракте ристи ка д л я и де а лиз иров а нной м оде ли а син х ронного эл е ктродвигате ля пр и прям ом п уске о т с е т и ча стотой 60 Г ц под на гр у зкой с п осл е д у ющ им с брос ом и на брос ом на груз к и. Для сра в н е н ия ре з у л ьтатов усл ов и я м оде л иров ания взяты, как указано в [10].

На рис. 3 и 4 п оказ а ны а налогичные р ис . 1 и 2 г ра фики той ж е м ашины, в урав не ния инд укт и вн ос те й с та т о ра и р ото ра к ото р ой а в то рам и в вед е ны поп ра вочные ко эф фицие нт ы KSS = 0,946 и KRR = 0,946.

С рав н е н ие графи ков пока зыв а е т, что проце ссы в и де а лиз иров анной а с и нх рон ной м а ш ине и в р е а л ьной м а ши не м ог у т су ще с тв енно отлича ться. Еще бол ьше е вл и ян ие ока зыв а е т испол ьз ов ание в мод ел и А М п опра в очны х ф у н кц и й.

Распределение магнитной индукции в зазоре машины, создаваемое при питании обмоток статора от инвертора напряжения, также отражается на форме распределении токов в обмотках ротора. Анализ этого распределения с учетом вращения ротора требует отдельного рассмотрения и здесь не приводится.

Система частотного управления с учетом поправок к модели асинхронной машины

Примером применения предлагаемых поправочных функций и поправочных коэффициентов может быть устройство управления электромагнитным моментом асинхронного двигателя с короткозамкнутым ротором, питающегося от автономного инвертора напряжения, в котором используются полностью управляемые транзисторы IGBT [20].

На рис. 5 приведена обобщенная структурная схема этого асинхронного электропривода с векторным управлением. Здесь обозначены [20]: 1 – релейный регулятор электромагнитного момента (РРЭМ); 2 – релейный регулятор потокосцепления статора (РРПС); 3 – автономный инвертор напряжения (АИН); 4 – задатчик интенсивности (ЗИ)

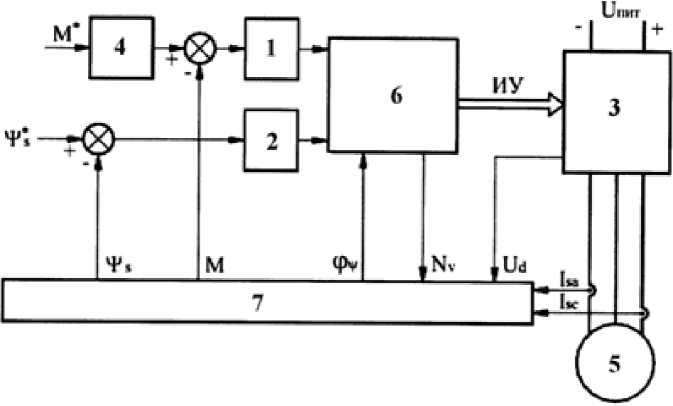
Рис. 5

нарастания момента (рывка); 5 – асинхронный двигатель (АД); 6 – блок ус та новк и пол ож ен ия вектора напряжения статора; 7 – в ы чи с л и те л ь п еременных.

П рин ц и п ра боты устрой с т в а по рис . 5 под р об но опис а н в пате н те [20]. Э ффе ктивнос ть оп и са нн ого а лгори тма у пра вл ени я пр ив одом обе с п е ч и в а ется в ыс оким быс тродейс твие м релейных ре гуляторов , точн ос тью обратны х с вяз е й с исте м ы р е г улиров а н ия, а та к ж е з а ви с ит от точнос т и с а м ой модели АМ.

Мат емат и ч еск ая мо д ель АМ о т р ажен а в пр и мен я емы х мат емат и ч е с к и х о п ер ац и я х о б ра бо т к и в хо д н ы х вел и ч и н : мг н о вен н ых зн ач ени й токов фаз статора, н а п р я жен и я ц е п и п о ст о я н н о г о то к а и н вер т о р а н ап р я жения, а т ак же в а лг о р и т ме раб о т ы к лю ч ей ( т р ан зи ст о р о в) и н вер т о ра н ап р я-

Us a m = U d [ S * M — ( S * M + S * M )]; u S P M = u d ^{( S}6M ^{+ S} * M ).

Затем вычисляют проекции вектора потокосцепления статора на оси неподвижной системы координат (α, β) с модифицированными значениями проекций векторов по следующим выражениям:

^ S a M = I ^{( u} S a M

^ S p M = J ^{( u} S Ф M

—

—

i S E M R_S ) ^dt ; i S p M R_S ) dt .

Далее вычисляют текущее модифицированное значение модуля вектора потокосцепления статора:

^ S a M = V ⁽ ^ S a M ) ⁺ ( ^ S p M ) .

жения.

Д ля АМ с н есину со и д а ль ны м р асп р ед елен и-

е м м аг н и т н о й и нду кц ии следу ет п р и мен ят ь мо-

ди ф и ци р о ван н ы е п р ео б р а зо ван и я век т о р о в н а комплексной плоскости (М-ПВ К) с и сп о ль зо в а ни ем п о п р аво ч н ы х фун кц ий и п о п р ав о ч н ы х ко-

эф ф и ц и ен т о в к п р ео б р аз о ван и ям Э. Кларк и Р. Парка [14–19].

Затем вычисляют текущее значение модуля электромагнитного момента с использованием модифицированных величин по выражению

M EM = 2 A⁽ ^ S a M i S P M ^—^ S P M i S a M ). ⁽²⁰⁾

Текущее модифицированное значение угла вектора потокосцепления статора вычисляют по выражению

В ычис л е н ие прое к ци й в е к тора тока с та тора на

Ф ^ = arccos ( ^ S e M / ^ SmM )

о с и н е п одвижной с исте мы коорди нат ( α, β) произ в одится по мод ифи ц иров а н ному п реобразованию Э. Кларк:

i s a M = KAa ( 0 ) ■ i sA — KAa ( n /3) ■ ^

i SB + i SC .

i s p m = 2 K Aa ^{( n} / 6 ) ' ⁽ i S B

;

В некоторых системах частотного управления используют векторы машины в системе координат ( d , q ), неподвижной относительно ротора. В этих случаях необходимо применить модифицированное преобразование Р. Парка [17]:

—

i S C ) .

[ i dqM ]

idM

_[ i qM _

= P M { i ap M ] =

В ычис л е н ие прое к ци й в ект ора в ых одного на пряж ени я а в тоном ного и нв ертора на пряж е н ия 3 на о с и н е п одви ж ной с исте мы к оордин ат (α, β)) следу ет прои з в од ить с пом ощь ю м одифи циров анн ых поправочными функциями ком м утацио нн ы х фу н кций S 1 М , …, S 6 М :

KAa ( 0 ) ■ cos 0 KAa ( 0 —n /2) ■ sin 0

■

i S a M

_[— KAa( 0 + n /2) ■ sin 0 KAa ( 0 ) ■ cos 0j [ i_{S e M}

. (22)

Приведенный способ управления электромагнитным моментом асинхронного электродвигателя с короткозамкнутым ротором необходим в электроприводе механизма поворота экскаватора,

где рывки (удары) опасны для механизмов [20]. Для других приводов с частотным управлением применение поправочных функции и поправочных коэффициентов будет аналогичным изложенному.

Заключение

• 1.    В статье показано применение модифицированного метода зубцовых контуров для расчета распределения магнитной индукции в зазоре асинхронных электродвигателей с реальными конструкциями обмоток.

• 2.    Показано на примере трехфазной петлевой двухпериодной обмоткой статора с укороченным шагом – Z = 36, p = 2, m = 3, y = 7, q = 3 отклонение от синусоидальной формы распределения магнитной индукции в зазоре асинхронной машины.

• 3.    Рассмотрено несоответствие несинусоидальной формы распределения магнитной индукции в зазоре у реальных асинхронных машин преобразованиям Э. Кларк и Р. Парка, основанным на синусоидальной форме этого распределения.

• 4.    Авторами предложены модифицированные преобразования Э. Кларк и Р. Парка с использованием поправочных функций и поправочных коэффициентов, пригодные для учета конструкции обмоток в системах частотного управления с реальными асинхронными машинами. Разработан программный комплекс на языке Visual С# для расчета поправочных функций и поправочных коэффициентов.

• 5.    Использование поправочных функций и поправочных коэффициентов не требует переработки созданных ранее систем частотного управления асинхронной машиной. Показан пример такого использования для частотного асинхронного привода поворота экскаватора.

• 6.    Авторы надеются, что широкое обсуждение и применение результатов проведенного исследования окажется полезным для совершенствования систем частотного управления электрическими машинами.