Методы и критерии индивидуальной (раздельной) идентификации подвижных объектов, движущихся в группе, пассивными цифровыми оптическими локаторами

Пассивный цифровой оптический локатор (ПЦОЛ) представляет собой комплекс разнесённых в пространстве цифровых теодолитов (ЦТ) с единым пространственно-временным обеспечением [1]. Система из двух и более ЦТ позволяет оценивать такие параметры движения летательного аппарата (ЛА), как координаты в избранной центральной системе координат (СК), скорости и ускорения.

Рассмотрим случай, когда в поле обзора ПЦОЛ попадает группа ЛА, двигающихся с высокой скоростью по одному курсу, и требуется раздельно оценить параметры движения каждого ЛА.

Как показано в [1], обработка траекторной информации при использовании ПЦОЛ условно может быть разбита на два этапа: первичную обработку и вторичную, что на практике и делается.

Первичная обработка заключается в определении угловых координат объектов наблюдения по зарегистрированным данным с каждого из теодолитов.

Вторичная обработка подразумевает совместную обработку данных с нескольких теодолитов и определение параметров движения каждого из наблюдаемых объектов в пространстве.

Известные методики первичной и вторичной обработки, как правило, подразумевают оценку параметров движения наблюдаемых объектов на этапе послесе-ансной обработки при участии человека-оператора. Однако в настоящее время с распространением цифровых каналов наблюдения на основе ПЗС-матриц и развитием вычислительной техники появилась возможность использовать оптические средства для локации объектов в реальном режиме времени.

В работе [2] показано, что к числу принципиальных задач пассивной оптической локации относится задача идентификации объектов наблюдения. Авторы предлагают идентифицировать цели в группе по пространственным признакам совместности пар измерений. Однако процедуры идентификации осуществляются без учёта параметров движения наблюдаемых объектов в местных СК измерительных пунктов, что приводит к быстрому росту количества вычислительных процедур с увеличением числа объектов в поле зрения и появлению ситуаций, приводящих к необходимости использования трёх и более измерительных постов для принятия однозначного решения.

Математическая модель траекторных измерений с возможностью идентификации

Изложенный подход в обобщённом виде может быть представлен следующей базовой математической моделью:

( x * ( i ), у ;( i ), z k ( i ), ) T = р^ x

X

■ Г L                                             И , (1)

P ud U ^Рперв ^Г X Цк , l ⁽ i ), Y /k , l ⁽ i )’ ^ 0 l ⁽ i )’ ^в 0 l ⁽ i ) J ’ ^V

- l=1                                                               J где Рперв - оператор первичной обработки траекторной информации; Рвтор - оператор вторичной обработки траекторной информации; Рид - обобщённый оператор идентификации наблюдаемых объектов; L - количество ИП; K - количество ЛА в группе; l е [1;L] - номер ИП; к е [1; K] - номер ЛА; i - номер текущего отсчёта времени ti; X*к (i), Y*к (i), Z*к (i) - оценки координат ЛА с номером к в декартовой СК по результатам траекторных измерений в момент времени i; v - вектор координат привязки теодолитов; XЦк,l (i), Y/k,l (i) - координаты ЛА с номером к в СК ПЗС-матрицы; a0l (i), P0l (i) - показания датчиков углового положения (ДУП) ИТ на ИП c номером l в момент времени ti.

В практических задачах координаты объекта на ПЗС-матрице X_Цк , l ( i ), Y_Цk , l ( i ) оцениваются по входному изображению I i ( x , y ) путём применения к нему операторов выделения движущихся объектов Р_выд и операторов оценки координат центров объектов Р_центр :

( X Цк, ( i ), Y /к , l ( i ) ) T = Р центр Г Р выд [ I ( x , У ) ] ] . (2)

При этом входное изображение может быть пред- ставлено в виде [3]:

I. ( x , У ) = b. ( x , У ) g i ( x , У ) +

+ fi ^{( x} , У ⁾⁽¹ - g i ^{( x} , У )) + 5 i ^{( x} , У )’

где I, (x, y) - наблюдаемое изображение, bi (x, y) и f (x, y) - интенсивности пикселей, принадлежащих соответственно фону и объекту, gi (x, y) - бинарная мас ка, характеризующая принадлежность пикселя движущемуся объекту, £(x, y, i) - аддитивный шум фотопри-ёмного устройства. Предполагается, что значение шумовой составляющей не коррелирует со значениями элементов изображения и их пространственными координатами и влияние шума на исходное изображение описывается аддитивной моделью. Соответственно, наиболее подходящим методом восстановления является пространственная фильтрация, которая, наряду с бинаризацией, снижает влияние данного эффекта.

Оператор выделения объекта решает задачу обнаружения объекта и его локализации (определение области D предполагаемого размещения наблюдаемого объекта в кадре).

Оператор оценки координат центра на основе интенсивностей пикселей, входящих в область D , оценивает координаты центра объекта.

Конкретный вид операторов Р выд и Р центр зависит от типа измерительного прибора и особенностей задачи.

В обобщённом виде задача обнаружения и локализации объектов на изображениях рассматривается в работе [3].

Метод выделения движущихся объектов, основанный на усовершенствованном методе межкадровой разности применительно к оптическим локаторам следящего типа, предложен в работе [4].

Методы вычисления координат центров для случая наблюдения точечных объектов, а также вопросы зависимости погрешности вычисления координат центров объекта от размеров проекции объекта на плоскость ПЗС-матрицы рассматриваются в работе [5].

Оператор первичной обработки в общем случае отображает координаты наблюдаемых объектов в СК ПЗС-матрицы прибора в СК измерительного пункта с учётом показаний ДУП:

Р перв : ( f  Y^ ( i )   X Цк , i ( i )) T ^ .

^ ^{( a} Цк , 1 ⁽ i )    ^в Цк , 1 ⁽ i ))

где X_Цк , l ( i ) и Y_Цk , l ( i ) - координаты объекта (цели) на изображении с ПЗС-матрицы прибора. f - фокусное расстояние объектива; а _Цк ,, ( i ) и в _Цк ,, ( i ) - соответственно азимут и угол места цели в местной СК ИП; 1 -номер ИП; к - номер объекта в кадре; i - номер текущего отсчёта времени t i . Он может строиться в различных вариантах, зависящих от разновидности измерительного прибора.

Оператор вторичной обработки строится на основе известной методики, приведённой в работе [1]. В общем случае он отображает совокупность угловых измерений объекта, полученных с ИП, в центральную СК (как правило, прямоугольную):

^Рвтор ^{: (( а} Цк ,1⁽ i ) ^в Цк ,1⁽ i )) , "• ,

( а Цк , L ( i ) в цk,L ( i )) T ) ^                                 (5)

^ ( X * ( i ) y ;( i ) Z* * ( i ) ) ;

где X * _к ( i ), Y * _к ( i ), Z * _к ( i ) - оценки координат ЛА в декартовой системе координат; а _Цк ,, ( i ) и в _Цк ,, ( i ) - азимут и угол места цели в местной системе координат ИП; 1 - номер ИП; k - номер объекта в кадре; i - номер текущего отсчёта времени.

Когда в поле зрения теодолитов попадает группа объектов, встаёт задача определения номеров объектов, совместно привлекаемых к обработке. Для её решения в модель (2) вводится оператор идентификации наблюдаемых объектов Р ид . Он осуществляет отождествление результатов первичной обработки в соответствии с выбранными критериями идентификации.

Критерии идентификации объекта наблюдения

В общем случае решение задачи идентификации сводится к построению функции правдоподобия всех возможных вариантов распределения измерений по траекториям и поиску её максимума, как показано в [6].

На практике же задача может быть решена путём вычисления матрицы расстояний между отождествляемыми измерениями по некоторой метрике и последующего выбора комбинаций измерений, которым соответствуют её минимальные элементы.

При этом задача идентификации разбивается на две подзадачи - пространственную и временную.

Пространственная идентификация подразумевает отождествление измерений, зарегистрированных различными постами на один и тот же момент времени, тогда как временная - измерений, зарегистрированных в разные моменты времени.

Рассмотрим пространственную идентификацию. Геометрия задачи показана на рис. 1 [2].

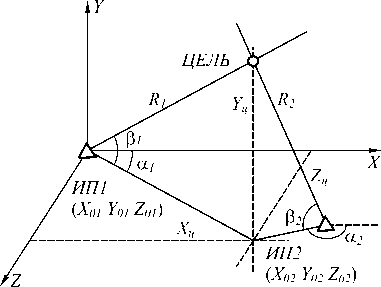
Рис. 1. Геометрия задачи пространственной идентификации: ИП1, ИП2 – измерительные пункты;

α1, β1 – координаты цели в СК ИП1; α2, β2 – координаты цели в СК ИП2; XЦ, YЦ, ZЦ – координаты цели в прямоугольной системе координат; X02, Y02, Z02 – координаты привязки ИП2 относительно ИП1

В радиолокации задача пространственного отождествления измерений решается методом пересечения пеленгов [7]. Аналогичный критерий пересечения пеленгов применительно к ПЦОЛ может быть сформулирован в следующем виде [2]:

R 1

R 2

= A

।-j

Y 0

= A

l-j

Z ₀

= A 3

Y 0

Z ₀

где X₀,Y₀,Z₀ – координаты привязки второго изме рительного пункта относительно первого ; A₁, A₂ , A₃ – матрицы преобразования координат .

Если пеленги не пересекаются , то решения разны ми способами дают различные результаты и условие не соблюдается . Строгого выполнения этого условия на практике не наблюдается ввиду того , что измерения выполняются с погрешностями . В связи с этим вводят ся допустимые пределы разностей расстояний A R * и A R 2 , значения которых выбираются исходя из плана расстановки измерительных приборов и их погрешно стей измерения угловых координат .

Далее рассмотрим временную идентификацию . Критерий отождествления измерений , зарегистриро ванных в соседние моменты времени , формулируется на базе принимаемой модели движения ЛА .

Во - первых , в соответствии с классом решаемых задач критерий может быть построен на основе из вестной модели прямолинейного движения ЛА , при ведённой в [7]:

S ₊ 1 = A i S i + ц , ,                                     (7)

где S = ( X k , , Y k , , Z k , , ^V _x , k , , V , k , , V z , k , , ) T ^{- ве}к— тор состояния ЛА в момент времени t_i (в данном случае рассматриваются координаты в трёхмерном про-

( E₃ E₃ T.)

странстве); a =            - составная матрица про* IO3    E3 J гноза, где E3 – единичная матрица 3×3, O3 – нулевая матрица 3X3, Ti = ti - ti-1 - промежуток времени между измерениями; цi - вектор нормально распределённых случайных величин с нулевым математическим ожиданием. Вектор цi может быть представлен в виде: цi = Uivi, где vi = (vx vy vz) - вектор уско-

( ( t? /2) E₃ )

рений ЛА, U. =            - матрица размерности

i I TkE3 J

6×3, характеризующая влияние ускорений на компоненты вектора состояния ЛА.

Критерий принадлежности очередного набора измерений S_i тому же объекту, которому принадлежат зарегистрированные ранее наборы измерений S i , и S i _{- 2}, формулируется следующим образом:

[ Vx <и x;

2 V y <и у ;                                           (8)

[ vz <и z;

где и _x , и _у , и _z - заданные пределы ускорения цели по каждой из осей координат.

В некоторых частных задачах, когда линейная модель изменения параметров ЛА применима не только к его координатам, но и каким-то другим наблюдаемым признакам (яркость, размер и т.п.), эти признаки и скорости их изменения могут быть также включены в вектор состояния цели S_i . Если требуется временная идентификация в угловых координатах измерительного пункта (по результатам первичной обработки без привлечения информации с других ИП), то вектор состояния цели будет складываться из угловых координат и угловых скоростей объекта в местной СК ИП, что будет рассмотрено далее.

Во-вторых, в основе критерия временной идентификации может лежать гипотеза о том, что наблюдаемые ЛА совершают групповое движение по одному курсу и, как следствие, отклонение произвольного ЛА с вектором состояния S_{k , i} от центра группы с течением

времени меняется незначительно.

Математическое ожидание [8] координат наблюдаемых объектов в момент времени t_i принимается в качестве координат центра группы объектов и имеет вид:

S0 = M (Х,„¥,„2„) T = i                        k,i k,i k,i

= f 1 y^K X 1 y^K Y 1 y^K Z

I K Д^к =1 ^k , i K Д^к =1 ^k , i K Д^к =1 ^k , i

T

.

Координаты некоторого ЛА относительно центра группы запишутся следующим образом:

SL = Ski k , i k , i

S_i 0 .

Для случая направленного движения группы объектов предлагается соотношение:

S^cc_i+ 1= Ski +ц,, k , i + 1           k , i         k , i

где ц _k , i = ( A X_k , i A Y_k , i A Z_k , i ) - вектор нормально распределённых случайных величин с нулевым математическим ожиданием, характеризующих случайные перемещения ЛА в СК, связанной с центром группы.

Тогда критерий принадлежности S n , i _{+ 1} и S_k , i одному и тому же ЛА для случая группового движения в трёхмерном пространстве в общем виде может быть сформулирован в виде:

'I^{A X}k , i | <  d Л x <|^A Y k , , | <  d Л у , J ^{A Z} k , i | <  d v ° z

где о _x , о _y , о _z - среднеквадратические отклонения компонентов вектора ц _k , i ; d _v - ширина доверительного интервала [8]. Эти параметры задаются заранее, например на основе результатов статистического анализа ранее зарегистрированных данных.

Сокращение перебора на этапе пространственной идентификации

Если в поле зрения L измерительных пунктов попадают K объектов (т.е. необходимо сформировать K наборов координат по L пар в каждом), то максимальное количество проверяемых гипотез пространственной идентификации составит K ^L . С увеличением количества объектов в поле зрения число гипотез растёт, причём согласно [2] проверять их требуется для момента времени каждого кадра. Под гипотезой идентификации здесь и далее будем понимать набор из L измерений (по одному с каждого ИП), относительно которых делается предположение об их принадлежности одному и тому же объекту. Нетрудно подсчитать, что для проверки одной гипотезы идентификации требуется не менее L -1 операций проверки критерия (6).

В многопозиционной радиолокации (при условии, что каждый ИП измеряет 3 координаты), как правило, проблему сокращения перебора при пространственной идентификации решают путём пространственного стробирования на основе показаний одного из пунктов и последующего отождествления измерений в пределах строба, как показано в [7].

В ПЦОЛ в силу отсутствия прямых измерений дальности применение аналогичного подхода нецелесообразно и требуется использовать другие подходы к оптимизации.

Один из возможных способов заключается в предварительной временной идентификации объектов на этапе первичной обработки.

В случае, когда вектор состояния цели S i содержит угловые координаты и угловые скорости ЛА, критерий временной идентификации (8) на основе линейной модели движения примет вид:

vр <и

V а <  ^U a ’

где и_р , u_c - заданные пределы угловых ускорений по углу места и азимуту соответственно. В удобной для практической реализации форме критерий запишется следующим образом:

I( F )²( в _1д - 2 в i - 1,1 +в i - 2,k )| p

| ^{( F ) 2 ( а} i , q ^{- 2 a} i -1, l ^{1 C} i -2, к )| < ^Uc/

где F - частота кадров, a i и в i - азимут и угол места объекта наблюдения в момент времени i .

Алгоритм межкадровой идентификации, основанный на данном критерии и ориентированный на применение в измерительных станциях следящего типа, предложен в статье [9].

Аналогично для случая, когда рассматривается движение группы целей в плоскости матрицы и требуется проверить принадлежность изображения объекта ( х_Цп , l , i , у_Цп , l , i ) тому же ЛА, которому принадлежит ^{( х}цк , i , i -1 , У цк , i , i -1 ), критерий идентификации ⁽¹²⁾ принимает вид:

|Хцп , i , i - ( X O + C x ( x_uw - X io -1 ))| <  d Л x

| У цп , i , i - ( Y + C_y ( У цк , 1 , i - Y J)| <  d v ° y ’

1 K _  1 K где Xi = "F^x»-l-i , Yi = "F^Уцк-l-i - оценки мате-K к=1               K к=1

матического ожидания координат наблюдаемых объ-

„     ai, x ектов в системе координат ПЗС-матрицы; C = —:— ai-1,x ai, У и C = —— - коэффициенты, обеспечивающие ин-y i-1, У вариантность к масштабу, где ai,x, ai1x, ai,y, ai_1 -средние линейные отклонения соответствующих координат для текущего и предыдущего кадров [8]:

a ix = | iKu - ^X -|; «. „ = | fk, i, - Y °| • ( ¹⁶ ) K к = 1                       K к = 1

На практике критерии идентификации (14) и (15) могут быть использованы совместно.

Поскольку для проверки предлагаемого критерия временной идентификации в виде (15) не требуются угловые координаты объектов наблюдения, он может быть применён непосредственно к координатам объектов наблюдения в пространстве ПЗС-матрицы, определяемым по формуле (2). При этом данный критерий применим для измерительных приборов как патрульного, так и следящего типов. В случае использования на измерительном пункте многопроцессорной ЭВМ, алгоритм, проверяющий данный критерий, может выполняться параллельно с алгоритмом первичной обработки траекторной информации.

Пусть g i - количество измерений, зарегистрированных на некотором ИП в кадре с номером i . По окончании процесса проверки критерия (15) станет известно количество измерений из кадра i-1, для которых удалось найти соответствующие измерения из кадра i . Обозначим это значение через p i . По нему можно оценить качество отождествления измерений внутри группы:

Q i = p . (17) g_i

Условие Q i = 1 означает, что для всех объектов, зарегистрированных в одном из рассматриваемых кадров и принадлежащих группе G i , удалось найти пару из числа зарегистрированных во втором кадре, что означает успешное отождествление всех измерений по предложенному критерию.

Измерения с текущего кадра, для которых не удалось найти соответствий, образуют множество Si е Ci. Они должны быть идентифицированы другим алгоритмом, например на основе критерия (14). Практика показывает, что критерий (15) обеспечивает выское качество идентификации в условиях, когда количество объектов в кадре не меняется и наблюдаемые ЛА движутся по одному курсу. В ситуациях, когда в поле зрения появляются новые объекты либо исчезают старые, значение Qi снижается и для идентификации привлекается критерий (14).

После окончания временной идентификации на ИП угловые координаты выделенных объектов и присвоенные им номера траекторий передаются на центральный пост, где осуществляется вторичная обработка. Соответственно, при пространственной идентификации на центральной ЭВМ методика полного перебора всех возможных пар измерений может быть заменена на псевдооптимальную, когда в первую очередь сопоставляются измерения, получившие такие номера траекторий, которые в предыдущие моменты времени были признаны совместимыми.

Результаты экспериментов

Эксперимент 1. Сравнивалось количество вычислительных процедур при проверке критерия пересечения пеленгов на этапе пространственной идентификации с использованием методики полного перебора и с учётом результатов предварительной временной (межкадровой) идентификации в угловых координатах. Результаты приведены на рис. 2.

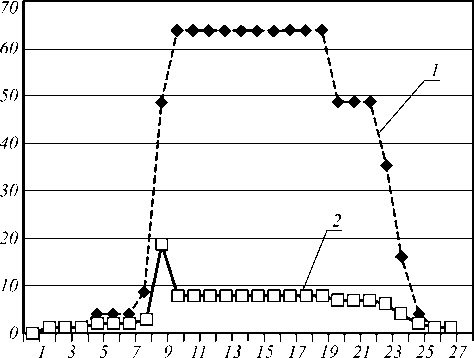
Рис. 2. Количество проверок критерия пересечения пеленгов в пассивном оптическом измерительном комплексе, состоящем из двух ИП:

• 1    – для метода полного перебора; 2 – для метода, учитывающего результаты временной идентификации

Моделировалась ситуация, когда в поле зрения ПЦОЛ из 2 ИП влетает группа из 10 объектов, некоторое время устойчиво наблюдается и затем покидает поле зрения. В соответствии с реальной ситуацией объекты появляются в поле зрения и исчезают не одновременно, а по очереди.

Причина выигрыша в производительности при пространственной идентификации заключается в том, что в случае предварительной межкадровой идентификации входные данные оказываются сгруппированы по признакам принадлежности к траекториям и перебор требуется только для новых объектов, появившихся в поле зрения теодолита в данный момент времени.

Эксперимент 2. Исследовалась результативность алгоритмов идентификации, работающих совместно по предложенной ранее схеме. Рассматривалась ситуация использования 2 ИП.

Погрешности оценок угловых координат моделировались нормально распределёнными случайными величинами с нулевым матожиданием [8] и СКО, соответствующими типовым ситуациям при использовании реальной аппаратуры. Моделировалось движение группы из 20 ЛА со скоростью 200 м/с в течение сеанса регистрации в 500 кадров при частоте 50 кадров/с.

Отдельно подсчитывалось количество ошибок идентификации, соответствующих следующим случаям:

• 1.    Ошибочная пространственная идентификация при верных результатах временной идентификации хотя бы на одном ИП.

• 2.    Одновременная ошибочная временная идентификация на обоих ИП.

Следует подчеркнуть, что появление одиночных ошибок ложного обнаружения либо пропуска цели на отдельно взятом ИП ещё не означает ошибочного результата работы комплекса в целом, поскольку ложные измерения отсеиваются на этапе вторичной обработки при проверке критерия пересечения пеленгов. То же самое касается случаев ошибочной временной идентификации.

Рассмотрим измерительный пункт ИП1. Если на этапе временной идентификации по итогам проверки критерия (12) или (13) некоторое измерение A_{i , ИП 1} , зарегистрированное в момент времени i и в действительности принадлежащее объекту, которому ранее на этом посту был присвоен номер траектории j _{1, ИП 1} , будет ошибочно отнесено к траектории с номером j _{2, ИП 1} , то на этапе пространственной идентификации при сопоставлении измерений ИП1 и ИП2 критерий пересечения пеленгов (4) не покажет соответствия между измерением A_{i , ИП 1} и измерением B_{i , ИП 2} с ИП2, которое при временной идентификации получило номер траектории j _{2, ИП 2} , который, в свою очередь, в предыдущие моменты времени присваивался измерениям с ИП2, которые отождествлялись с измерениями с ИП1, имеющими номер траектории j _{2, ИП 1} . Затем во множестве неидентифицированных измерений с пункта ИП2 по критерию пересечения пленгов (4) будет найдено измерение A_{i , ИП 2} , которое совместимо с измерением A_{i , ИП 1} и соответствует тому же объекту в действительности. Таким образом, одиночные ошибки временной идентификации исправляются на этапе пространственной идентификации.

Если события «ошибочная временная идентификация на ИП1» и «ошибочная временная идентификация на ИП2» считать независимыми, то вероятность одновременного их наступления можно оценить по формуле умножения вероятностей [8].

Полученные показатели качества идентификации при различных значениях СКО ошибок измерения угловых координат приведены в табл. 1.

Таблица 1. Результаты имитационного эксперимента

№ п/п	СКО погрешностей оценок угловых координат, угл.с.		Количество случаев ошибочной идентификации, %		Количество верно идентифицированных объектов, %
	σ АЗ	σ УМ	Вызванных ложным отождествлением пеленгов	Вызванных одновременным ложным отождествлением измерений обоими ИП либо потерей цели
1	1	1	0,01	0,02	99,9
2	5	5	0,52	0,1	99,4
3	10	10	2,11	0,58	97,3
4	20	20	8,3	2,08	89,6
5	30	30	16	4,6	81,4

Заключение

• 1.    Предложенная модель обеспечивает решение задачи идентификации при обработке траекторной информации в распределённой вычислительной системе и возможность комбинирования методов идентификации c получением приемлемых результатов с использованием всего двух ИП.

• 2.    Разработанные алгоритмы обеспечивают сокращение количества вычислительных процедур на этапе пространственной идентификации, что позволяет расширить область применения ПЦОЛ, например, для оперативного контроля воздушного пространства и оперативной оценки результатов полигонных испытаний современных видов оружия, а также могут быть использованы в других областях, где требуется идентификация быстродвижущихся групповых объектов.

• 3.    Одним из перспективных направлений дальнейшего развития пассивных оптических комплексов траекторных измерений представляется введение в математическую модель, наряду с рассмотренными в данной статье операторами идентификации по координатным признакам, операторов идентификации, основанных на признаках формы, размера и распределения яркости объектов, что позволит повысить качество идентификации в ряде частных случаев и существенно расширить сферы применения подобных систем.