Методы и проблемы калибровки космических магнитометров на анизотропном магниторезистивном эффекте

Магнитометры широко применяются на космических аппаратах (КА) в системах ориентации и стабилизации (СОС), также они являются ключевым компонентом научных исследований в части изучения Земли и других планет солнечной системы.

В настоящее время в СОС большинства низкоорбитальных КА входят магнитометры, изготовленные с применением анизотропной магниторезистивной технологии (АМР) [1–3], что обосновано малым весом, размером и энергопотреблением такого прибора. В СОС магнитометры применяются с целью определения величины и направления вектора магнитного поля Земли. Полученная информация используется для расчёта управляющих моментов КА, например для стабилизации вращения КА управляющие моменты формируются электромагнитными исполнительными органами (катушками) по показаниям магнитометра.

Однако основной проблемой АМР магнитометров является необходимость оценки возможных ошибок измерений, т. е. необходимость проводить калибровку прибора. С целью решения представленной проблемы исследователи предлагают различные методы оценки и ослабления ошибок, влияющих на измерения [2–7].

Следует упомянуть также о том, что ошибки не разделяются на периодические и постоянные, они объединяются в общей методике калибровки, которая представляется универсальной для различных типов магнитометров и областей их применения. Основными параметрами, которые подвержены калибровке, являются величина смещения выходной характеристики, коэффициенты наклона выходной характеристики (коэффициенты чувствительности), коэффициенты неортогональности (отклонение осей чувствительности прибора от осей прибора).

В статье будут рассмотрены основные направления в методиках калибровки космических магнитометров и кратко описаны следующие составляющие методик:

– математическая модель с учётом ошибок;

– оборудование;

– операции, проводимые на комплекте оборудования.

Ошибки, вызванные магнитомягкими материалами

Магнитомягкие материалы в составе конструкции прибора формируют собственное магнитное поле под воздействием внешнего. Направление и величина вектора магнитного поля, генерируемого магнитомягкими материалами, может изменяться в широком диапазоне, что во многом зависит от материала, формы элемента и приложенного вектора внешнего магнитного поля. В результате такого воздействия формируется ошибка с зависимостью от внешнего магнитного поля, часто её представляют как матрицу «магнитомягких ошибок» [4]:

	axx   a     axz xx xy xz
D si =	a yx    a yy    a yz _ a zx    a zy    a zz _

В некоторых случаях она может быть упрощена путём исключения недиагональных элементов матрицы.

Также следует упомянуть, что коэффициенты матрицы D si являются линейными только в условиях малой величины внешнего магнитного поля, так как относительная магнитная проницаемость сред µ, а следовательно, и коэффициенты, не линейны при средних и больших значениях магнитного поля [4; 8].

Коэффициенты преобразования

У любого АМР датчика по каждой из осей чувствительности имеется свой коэффициент преобразования, обычно это преобразование величины магнитного поля в выходную величину напряжения, таким образом размерность коэффициента преобразования k [мВ/(В·мТл)], где «мВ» – величина выходного сигнала при напряжении питания U _{пит ЧЭ} «В» и магнитной индукции «мТл». Выходная величина чувствительного элемента (ЧЭ) может быть усилена и оцифрована. Отразить эти коэффициенты в математической модели можно следующим образом [7]:

S =

kx

- 1

k y

- 1

kz-1

• U пит ЧЭ ’

Следует также отметить, что на практике при наличии ЧЭ в составе прибора разделить диагональную матрицу D si и S не представляется возможным, таким образом калибровочные коэффициенты определяются для их произведения.

Смещение

Смещение можно разделить на три вида, где первое – это технологическое смещение датчика, второе – это смещение выходного сигнала прибора под действием магнитотвёрдых материалов (постоянные магниты при условии отсутствия внешних полей, способных их перемагнитить) и токовых контуров, третье – периодическое воздействие полей, создаваемых КА.

Все перечисленные виды накладываются друг на друга, и, как правило, в процессе калибровки их не разделяют:

b = [ b x , b y , b x ] •

Неортогональность

ЧЭ, изготовленные на тонкоплёночных элементах, не отличаются прецизионной точностью расположения осей чувствительности. Откуда возникают ошибки, связанные с неортогонально-стью осей чувствительности друг к другу, как указано на рис. 1:

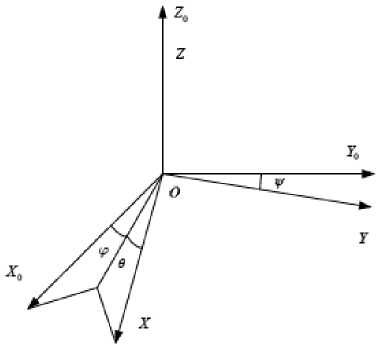
Рис. 1. Схематическая модель неортогональности, где X 0 , Y 0 , Z 0 – ортогональный базис

Fig. 1. Schematic model of non-orthogonality, where X ₀, Y ₀, Z ₀ is the orthogonal basis

Обычно неортогональность описывается матрицей поворота, например [9]:

cos(φ) cos(θ) sin(φ) cos(θ)

C NO =

0          cos(ψ)

sin(θ) sin(ψ) 1

Несоосность

Помимо неортогональности осей чувствительности прибора, оси, как правило, располагаются не соосно с осями прибора, что также требует некоторой математической корректировки, например при помощи матрицы поворота (углов Эйлера) [10]:

cos(β) cos(γ)

C NS = sin(a) sin(e) cos(y) + sin(y) cos()

sin(a) sin(Y) - sin(e) cos(a) cos(y)

- cos(e)sin(Y)                 sin(e)

- sin(a) sin(e) sin(y) + cos(a) cos(y) - sin(a) cos(e) sin(a) cos(y) + cos(a) sin(e) sin(Y) cos(a) cos(e)

Матрица поворота C будет являться произведением матриц C_NO и C_NS .

Температурная зависимость

Температурная зависимость АМР датчиков и магнитометров является достаточно серьёзной и вездесущей проблемой, о которой на удивление мало написано. Несмотря на то, что физические свойства чувствительного элемента подразумевают устранение температурного смещения, производственные дефекты пермаллоевых плёнок и температурная зависимость напряжения питания ЧЭ и аналого-цифрового преобразователя (АЦП) играют существенную роль в формировании выходных значений прибора.

Обобщённо, температурная зависимость может быть выражена в следующем виде [1]:

KT

kxx   kxy   kxz

kkk yx     yy     yz

kkk zx      zy      zz

Математическая модель измерений прибора с учётом ошибок

Ранее мы перечислили некоторые ошибки, свойственные для большинства магнитометрических датчиков и магнитометров. Составляя математическую модель, исследователи зачастую отражают в ней все известные эффекты, влияющие на показания прибора (рис. 2).

Трёхосевой магнитометр

Ошибки, вызванные внешними	Ошибки, вызванные внешними	Ошибки, вызванные
факторами	факторами и чувствительным элементом	чувствительным элементом

Несоосность осей чувствительности ЧЭ и осей прибора

Магнитный момент и токовые контуры

Шум измерений

Магнитомягкие материалы

Различная чувствительность каждого магнитометра

Неортогональность осей чувствительности

Магнитотвёрдые материалы и смещение нуля

Температурное смещение сигнала и деформация платы

Рис. 2. Ошибки, влияющие на показания АМР магнитометра

Fig. 2. Errors affecting the AMR magnetometer readings

Процесс калибровки некоторых из перечисленных ошибок весьма ресурсозатратный и не приносит большого выигрыша в точности, по этой причине математическую модель упрощают до состояния, при котором возможно определить все её элементы наименее затратно и с требуемой точностью.

Математическая модель, по нашему мнению, будет выглядеть следующим образом, что отличается от модели, предложенной в работе [1]:

B дейст = ( S • C • D si + K t • T ) • U маг - S • C • D si • ( b + К ть • T ),

где B _действ – вектор эталонного магнитного поля (мТл), полученного по показаниям эталонного магнитометра или иным способом; T – скаляр температуры магнитометра (° C ) (в случае компоновки ЧЭ и блока электроники в одном корпусе – температура чувствительного элемента); K Tb – вектор температурных коэффициентов смещения нуля (мВ/° C ); U маг – вектор выходного сигнала магнитометра (мВ); b – выходной сигнал прибора при отсутствии внешнего поля и нормальных условиях (мВ).

Основной задачей процесса калибровки магнитометра является поиск всех составляющих элементов математической модели. Прибор считается откалиброванным, если при подстановке измерений B _маг, при различных внешних условиях в математическую модель результат её вычисления не отклоняется от показаний эталонного прибора более чем на величину, определяемую требованиями по точности прибора.

Методики калибровки

Методики калибровки магнитометров можно разделить на две категории:

• –    зависимые от положения – требуют высокоточных данных об ориентации осей прибора (и КА, в случае лётной калибровки);

• –    независимые от положения – применяются в условиях отсутствия точной информации о положении осей чувствительности магнитометра относительно эталонного магнитного поля.

Следует отметить, что математические методы, применяемые в обеих категориях, весьма схожи, однако при отсутствии данных о положении параметры матриц [ S·C·D si ] не поддаются наблюдению и не могут быть определены [11; 12]. Полностью заполненная матрица с 9 независимыми коэффициентами в условиях космического пространства может быть вычислена только в том случае, если известно положение космического аппарата и расположение осей чувствительности прибора в связанной с КА системе координат [13].

Проводя сравнение наземной и лётной калибровки магнитометров, следует отметить, что многие исследователи считают процесс наземной калибровки весьма сложным [13, 14]. Подобное мнение оправдано необходимостью применения прецизионно точного оборудования и систем, а также места испытаний, защищённого от магнитных помех. Более того, механические воздействия при выведении КА на орбиту могут стать причиной дополнительных ошибок, неучтённых при проведении наземной калибровки. С целью решения указанных проблем на Земле проводится грубая калибровка с последующей корректировкой параметров на орбите.

Однако СОС КА магнитометры также применяются в режиме успокоения аппарата после отделения от ракеты-носителя, что в свою очередь требует быстрого реагирования прибора и не позволят повысить его точностные характеристики вплоть до перехода в режим трёхосной стабилизации КА. Исходя из описанного, для СОС КА, в которых магнитометр является основным прибором режима успокоения, особенно важно проведение точной наземной калибровки.

Применяемое оборудование при наземной калибровке

Как было указано ранее, для проведения испытаний необходимо обеспечить отсутствие каких-либо магнитных помех в рабочей области стенда. В первую очередь, для осуществления данной задачи избегают применения каких-либо магнитных материалов и проводников с током в непосредственной близости к испытательному стенду. Желательно также изолировать стенд магнитных испытаний и посадочные места магнитометров от цепей заземления. Для исключения помех техногенного характера установку могут расположить вдали от городов, ЛЭП или под землёй [5].

Отдельно следует упомянуть о применении магнитного экранирования. При необходимости достижения наилучшей стабильности и исключения магнитных вариаций геомагнитного поля (зависит от широты и солнечной активности) [15] испытательный стенд размещают в экранирующей камере, изготовленной из трёх (или более) слоёв материала с высокой магнитной проницаемостью (пермаллой или сталь), разделённого немагнитными слоями. Необходимо заметить, что объём камеры должен быть достаточен для того, чтобы аппаратура, расположенная внутри, не наводила дополнительных помех посредством взаимодействия переменного поля аппаратуры и материала камеры, также это обосновано эффективной зоной работы магнитного экрана [16].

Следующей важной частью стенда является устройство, позволяющее устанавливать величину и направление вектора магнитной индукции в рабочей области стенда. С этой целью применяются различные соленоиды и постоянные магниты, однако наиболее широко распространено применение системы колец Гельмгольца и её различных модификаций, таких как системы колец Максвелла, Баркера, Браунбека (рис. 3) и Гаррета [17]. Особенностью всех перечисленных систем является высокая степень однородности магнитного поля в рабочей области. Рабочий диапазон и точность колечной системы могут быть настроены в соответствии с требованиями к стенду при помощи подбора числа, диаметра и формы витков катушек, а также программируемого источника питания. Следует отметить, что, применяя трёхосные колечные системы, возникает возможность установки вектора магнитного поля рабочей области в любом желаемом направлении.

Важным инструментом, влияющим на результат калибровки, является источник данных о направлении и величине истинного (эталонного) магнитного поля в рабочей области стенда. Чаще всего данные об эталонном магнитном поле в рабочей области получают с эталонного феррозондового магнитометра [1; 6]. При отсутствии помех техногенного характера, эталонный магнитометр может быть установлен на значительном расстоянии от стенда с целью определения величины и направления геомагнитного поля. В подобной компоновке эталонный магнитометр не будет влиять на магнитное поле рабочей области стенда, а данные о магнитном поле рабочей области будут определены математически, исходя из характеристик системы колец стенда и токов в их обмотках. Калибровка может быть проведена только с применением системы колец, однако в таком случае будут отсутствовать точные данные о геомагнитном поле Земли (начальном поле при отсутствии тока в колечной системе), что приведёт к дополнительным погрешностям во время калибровки. Следует напомнить, что некоторые методы предусматривают отсутствие точных данных о величине и направлении магнитного поля [5; 6; 11], таким образом, для проведения калибровки достаточно знать модуль вектора магнитной индукции в месте проведения испытаний, например, используя данные модели Международной ассоциации геомагнетизма и аэрономии (МАГА или IAGA ).

Ещё одним устройством, применяемым в ряде методик, является поворотный стол. Обычно он применяется при отсутствии трёхосной колечной системы [18] или в качестве дополнительного оборудования для неё [6].

При необходимости проведения температурной калибровки, для проверок в области отрицательных и положительных температур, возможно применение климатической камеры. Камера изготавливается из немагнитного непроводящего материала (рис. 3) [6] (при объёме значительно большем объёма колечной системы может быть изготовлена из проводника). В случае, когда точно известен характер температурной зависимости прибора, то достаточно применения нагревательного элемента [1].

Проводимые операции

Целью проведения калибровки является определение всех коэффициентов рассматриваемой математической модели. Модель определяется исходя из требований к прибору, доступного оборудования и ресурсов. Перечень проводимых операций над магнитометром определяется нахождением составляющих модели.

Нулевое или технологическое смещение прибора «b» при нормальных условиях

• 1.    При использовании трёхосной колечной системы проводится компенсация геомагнитного поля Земли и постоянных наводок от контуров с током и магнитов путём подачи рассчитанной величины тока в систему колец. При выполнении указанной операции используются данные эталонного магнитометра или расчётные данные. Применение расчётных данных влечёт некоторую погрешность, поскольку они не предусматривают суточных вариаций магнитного поля Земли и влияния техногенного фактора.

• 2.    При использовании одноосной колечной системы совместно с эталонным магнитометром компенсация проводится только вдоль одной оси.

• 3.    При отсутствии колечной системы, наличии эталонного магнитометра и поворотного стола, ось стола выставляют перпендикулярно магнитному меридиану (эталонный магнитометр покажет отсутствие магнитной индукции вдоль определённого направления).

• 4.    При отсутствии оборудования магнитометр выставляют одной осью вдоль магнитного меридиана (прибор покажет максимальное или минимальное значение).

Рис. 3. Пример внешнего вида стенда магнитных испытаний [6], где применяется система колец Браунбека, испытуемый и эталонный магнитометры расположены на поворотном столе в термокамере (жёлтый ящик), термокамера устанавливается в центр колечной системы при помощи каретки

Fig. 3. An example of the appearance of a magnetic test stand [6], where the Brownback ring system is used, the test and reference magnetometers are located on a turntable in a thermal chamber (yellow box), the thermal chamber is installed in the center of the ring system using a carriage

Выполняя указанные операции, возможно определить технологическое смещение прибора (показания прибора при отсутствии внешнего поля). Следует отметить, что некоторые магнитометры (как правило, космические) не способны работать в условиях магнитного поля Земли (60 мкТл), поскольку их диапазон измерений значительно меньше и варьируется от области применения прибора, например в миссии TRIO-CINEMA применялся АМР магнитометр с рабочим диапазоном ± 50 мкТл, а в Europa Clipper mission – феррозондовый магнитометр с рабочим диапазоном ± 4 мкТл, по этой причине без проведения компенсации поля по трём осям проводить наземную калибровку некоторых космических магнитометров не представляется возможным.

Определение углов отклонения осей чувствительности от осей прибора «C·Dsi» при нормальных условиях

На данном этапе осуществляется вращение вектора магнитной индукции в плоскости каждой из трёх осей. В случае невозможности вращения вектора вращается прибор. При отсутствии точных данных о положении вектора эталонного поля, точно определить углы отклонения осей чувствительности не представляется возможным.

Определение коэффициентов наклона характеристики «S·C·Dsi» и линейности

На данном этапе магнитное поле поочерёдно прикладывается вдоль осей чувствительности прибора, строится выходная характеристика (градуировочная характеристика) для каждой из осей по данным прибора при разной величине поля. Зная выходные характеристики по каждой из осей чувствительности при известном магнитном поле, определяется нелинейность выходной характеристики (Гистерезис).

Следует отметить, что возможно объединить операции по определению углов отклонения, коэффициентов наклона и ленейности, прикладывая поле вдоль оси прибора, последующая обработка измерений позволит определить матрицу [ S·C·D si ] и величину нелинейности, однако, вследствие анизотропии магнитомягких материалов корпуса прибора, матрица [ S·C·D si ] будет определена с некоторой погрешностью.

Определение матрицы [S·C·Dsi]

Методы, не предусматривающие наличие точной информации о положении (при отсутствии эталонного магнитометра), полагаются исключительно на калибровку при помощи «сферического» вращения прибора в однородном магнитном поле [4; 9; 13], предполагая, что величина вектора магнитной индукции постоянна (рис. 4).

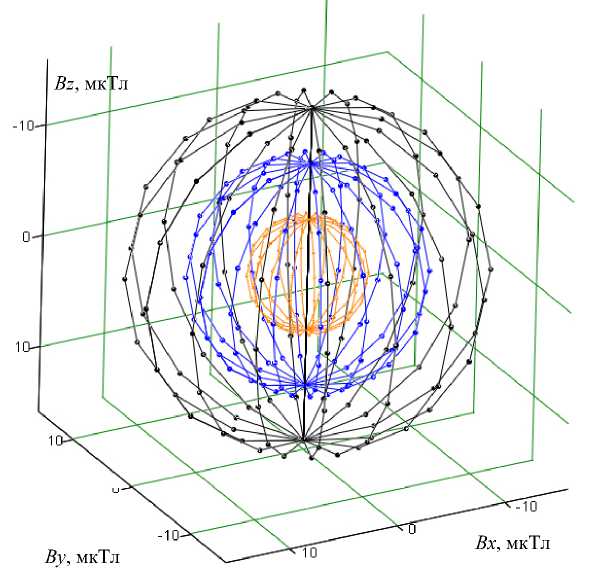
Рис. 4. Модели вращения вектора магнитного поля при шаге углов поворота θ j = 22,5°, φ i = 22,5° (углы азимута и высоты) и различной величине модуля вектора магнитного поля: B = 15 мкТл (чёрный), B 2 = 10 мкТл (синий), B 3 = 5 мкТл (оранжевый)

Fig. 4. Models of rotation of the magnetic field vector at a step of rotation angles θ _j = 22,5°, φ_i = 22,5° (azimuth and elevation angles) and different magnitudes of the magnetic field vector modulus: B = 15 µT (black), B 2 = 10 µT (blue), B 3 = 5 µT (orange)

При недоступности данных об эталонном поле, на данном этапе также применяют датчики скорости углового вращения [19; 20] прибора в постоянном магнитном поле. Применение трёхосной колечной системы позволит также определить величину гистерезиса выходных характеристик и градуировочную характеристику по каждой из осей чувствительности.

Определение температурных коэффициентов KTb и KT

На данном этапе проводится нагрев и охлаждение прибора с целью выявления температурной зависимости на коэффициенты S·C·Dsi. В целях лабораторных исследований работа ведется как в положительном, так и в отрицательном диапазоне температур, проводятся операции, описанные ранее. Следует отметить, что, в зависимости от принятой методики испытаний, повторение операций, описанных выше, может не проводиться или проводиться не в полной мере. В целях экономии времени, при известном характере температурной зависимости достаточно провести измерение технологического смещения и определить коэффициенты наклона выходной характеристики при положительных температурах.

Порядок калибровки с включением всех ранее рассмотренных этапов представлен на рис. 5.

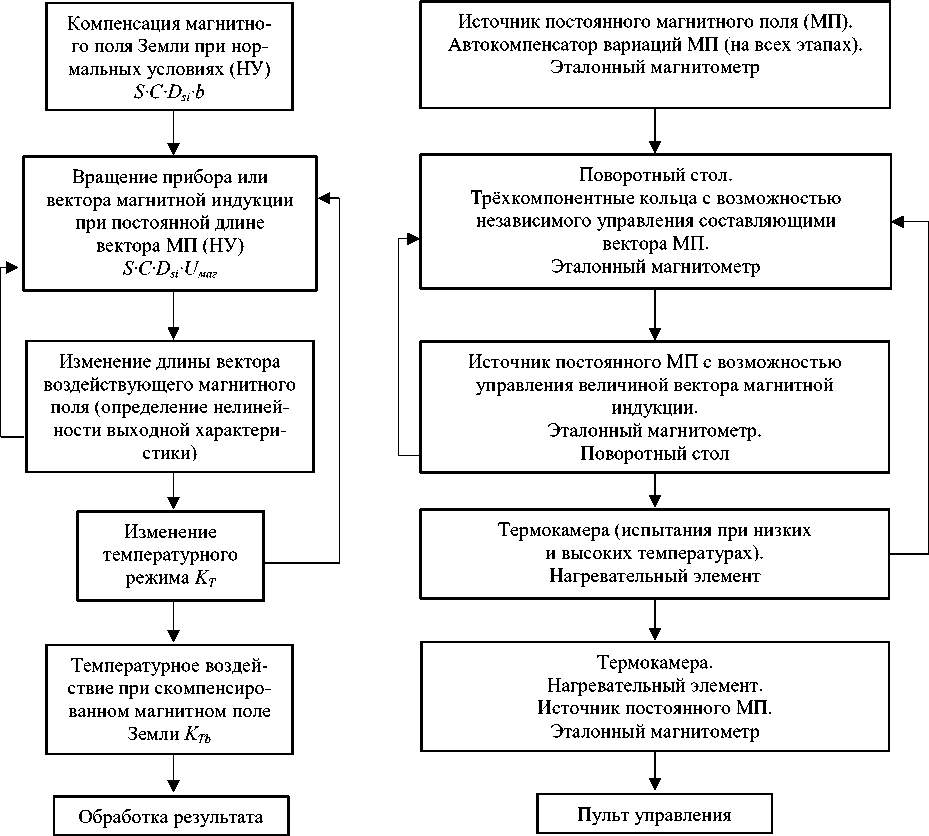
Рис. 5. Образец структурной схемы порядка калибровки (слева) и применяемого на этапах на соответствующих этапах оборудования (справа)

Fig. 5. A sample of the block diagram of the calibration procedure (left) and the equipment used at the stages at the corresponding stages (right)

Заключение

В представленной работе были рассмотрены методы проведения калибровки магнитометров на анизотропном магниторезистивном эффекте. Определены требования к оборудованию и месту проведения испытаний. Перечислены ошибки, влияющие на показания АМР магнитометра и пример их математического моделирования.

При этом методику определяет математическая модель на основе требований к прибору, также большое значение при выборе методики придаётся времени, затрачиваемому на проведение калибровки, и возможностям применяемого оборудования.

Основной задачей любой методики является обеспечение поиска коэффициентов, определённых математической моделью. С этой целью подбирается и дорабатывается оборудование, производится выбор и подготовка места испытаний, иначе – корректируется математическая модель.

Причиной необходимости применения сложных и дорогостоящих испытательных стендов для калибровок космических магнитометров на АМР эффекте является неповторяемость свойств магнитометров (например, направления осей чувствительности), невозможность их физической подстройки и в случае совместного расположения чувствительного элемента и блока электроники (на одной плате) значительное влияние магнитомягких материалов [2].

В связи с указанными причинами разрабатываются новые методы и математические модели, позволяющие при наименьших затратах по времени и при помощи наименее дешёвого оборудования обеспечить требуемые от прибора характеристики.