Методы и средства малоракурсной томографической диагностики параметров потоков ионных и плазменных двигателей космических летательных аппаратов

Перспективными двигателями для освоения ближнего и дальнего космоса в настоящее время и в течение обозримого будущего являются ионные и плазменные двигатели (ИПД). Многочисленные исследования [ 1 ] показали, что ускоряемый аппарат с помощью ИПД будет более эффективным при движении в космосе по сравнению с традиционными ракетами. В качестве основного (маршевого) двигателя ионный двигатель был впервые применён на космическом аппарате Deep Space 1. Предполагается, что 200-мегаваттный двигатель класса VASIMR [1, 2] сможет осуществлять миссии по доставке людей к Марсу всего за 39 дней.

Основными параметрами ИПД, как известно, являются отношение тяги к массе, скорость истечения ионной струи, симметрия вектора тяги по отношению к оси двигателя [3]. Наиболее эффективными методами решения такого рода задач являются спектрально-томографические методы диагностики параметров рабочего тела ИПД. Несмотря на то, что эти методы диагностики параметров плазменных потоков в оптическом диапазоне довольно широко развиты, их применение для исследования параметров потоков ИПД всё ещё не получило соответствующего применения.

Разработчики ИПД выбирают традиционные пути диагностики параметров струй [ 4, 5 ] , основанные на классических преобразованиях Абеля, уравнения Фредгольма 1-го рода. Основным недостатком такого подхода является то обстоятельство, что искомая функция распределения, например, локальных температур по объёму факела [ 6 ] , заведомо считается осесимметричной, что не так [ 4, 6 ] .

Следовательно, разработка новых методов и средств для решения задач 3D-реконструкции функций распределения исследуемых параметров рабочих тел ИПД является актуальной задачей.

1. Методы спектрально-томографической диагностики параметров рабочих тел ИПД

Задача исследования ионно-плазменного потока ИПД, во-первых, должна способствовать совершен- ствованию конструкций этих систем, а во-вторых, позволять решать фундаментальные вопросы: восстановления 3D-функций распределения ионной компоненты, локальных значений температур.

Автором разработан ряд методов 3D-томографи-ческой реконструкции параметров плазменных объектов применительно к диагностике ИПД. Эти методы оказались просты с точки зрения аппаратной и программной реализации. Точность реконструкции удовлетворяет предъявляемым требованиям. Алгоритмы, построенные на их основе, обладают высоким быстродействием, могут быть реализованы на стандартных ПК либо в кластерных системах.

В общем случае для оптически прозрачной плазмы функция проекции в направлении р определяется как [ 7 ] :

I (р, ^, X) = J е( r, X)d l, (1)

∆l здесь ξ, λ – параметры потока излучения в данном ракурсе (ξ – эффективность регистрации, λ – длина волны), ∆l – область определения функции проекции, г (r, X) - локальное значение коэффициента излучения. Уравнение (1) является интегральным уравнением первого рода, общее решение которого в интегральной геометрии известно как преобразование Радона 9 от функции е(r, X), то есть:

А I—             —I

9 [е( r, X)] = I (р, ^, X).

В полярной системе координат (ПСК) обратное преобразование Радона определяется [7] следующим образом:

е (I r, X) = -X ) d^Mpl^. -ip-

2π2 0 0 ∂p     p0 - p

.

С учётом p 0 = r sin( θ – ξ )(3) удобнее записывать в операторной форме:

е (r, X) = BHyDyI (p, ^, X), 2π

здесь B – оператор обратного проецирования, H Y – оператор Гильберта, D y - оператор дифференцирования по первой переменной.

Главной особенностью задач типа (1) оказывается их некорректность в классическом смысле. В действительности регистрируемые функции проекции являются приближенными функциями в смысле Радона. Следовательно, речь может идти о поиске приближенных решений. В дополнение к этому ситуация усугубляется тем, что при оптических методах регистрации вносятся дополнительные искажения в (1), появляются искажения при вычислении преобразования Гильберта и пр.

/(г)

а)

(g(n)

О1

Л2

D

в)

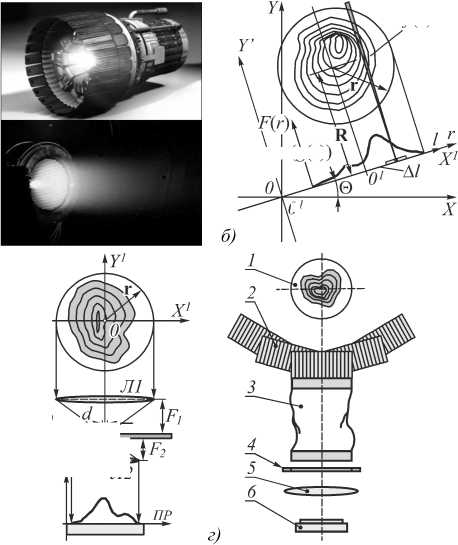
Рис. 1. Иллюстрации способов формирования исходных проекционных данных: внешний вид ИД (а), геометрия получения проекций (б), системы регистрации (в, г)

Ж

рис. 1 а )), то несложно организовать геометрию формирования исходных проекционных данных (рис. 1 б )) собственного излучения в ортогональной форме с помощью линзовых (рис. 1 г ) или коллимационных систем (рис. 1 в )). В строгой постановке задача оптической томографии заключается в реконструкции функций распределений, позволяющих анализировать процессы, протекающие в каждой локальной области исследуемого объёма. Так как в каждом микрообъёме в данный момент времени протекают процессы, присущие только этой области, сопровождающиеся излучением фотонов, то спектральный анализ излучения в совокупности с возможностями томографической реконструкции позволяют совершенно на новом уровне анализировать исследуемые явления. Локальный детектор в любом случае регистрирует излучение совокупностей микрообъёмов объекта в выбранном направлении данного сечения, интенсивность которого можно определить в виде:

а/2 I ₂ ( x ,0) f (/R)

I = f d p ² l d l • ^{fx (}., ^{e )} (5) -a/2 1 1 ( x ,0) l ²

здесь f x ( l , в ) - функция, характеризующая локальное излучение, в направлении l (рис. 1 б )). Если f x ( l , в ) непрерывна на круге, в который она может быть вписана, а параметры выбраны так, что a <<( r / R )<<1, то в соответствии с теоремой о среднем можно записать:

a I 2 ⁽ x ,0)

¹ = R J 1 1 ( x ,0) ^{d lf 1 ( l} ’⁰⁾”

Действительно, при указанных условиях отсчёты в проекциях пропорциональны интегралам от интенсивности вдоль оси фотодетектора, то есть удовлетворяют условию (2) и действительно могут рассматриваться как отсчёты томографических проекций. Для ионных потоков с относительно высоким уровнем осевой симметрии целесообразно применить быстродействующий свёрточный алгоритм на основе решения интегрального уравнения Шлёмильха с соответствующим ядром [ 8 ] :

1 -n x /2 a ,     |x | <  a ;

1 - ( x / a ) arcsin( a / x ), | x | >  a .

Для исследования параметров плазмы, вырабатываемой многопотоковыми ИПД-системами, которые сгруппированы в тяговую матрицу, данный подход малопригоден. В таких ситуациях необходимо применять так называемые низкочастотные динамические ядра вида:

1 n| 0,76 l|

2 B

I ^l l <  B ,

h ( l ) = ^

, 0,76 1      . B )

1--arcsin , l >  B .

B         (1,24 1 J ¹¹

Здесь B определяет ширину главного максимума ядра свёртки, то есть определяет его частотные свойства. Частотные свойства рассмотренного метода рекон- струкции оказываются выше, чем при использовании ядер вида (7). При этом значение B должно выбираться автоматически в зависимости от ширины главного максимума Фурье – спектра данной проекции.

При томографическом исследовании потоков ИПД, в силу ряда технических причин, количество исходных проекций оказывается ограниченным. Для оценки возможностей методов томографической реконструкции параметров таких потоков, целесообразно определить спектральное разрешение алгоритмов восстановления. Информационная способность алгоритма реконструкции, при всех прочих равных условиях, определяется не только числом исходных проекций, но и выбором ракурса каждой проекции. Заметим, что при всех прочих условиях необходимо привести реальные проекционные данные к виду, позволяющему воспользоваться обращением Радона, например, в виде:

∂ Rf(l,θ)/∂l dl. (9) rcos(θ-ϕ)-l

π∞ f ( r , ϕ ) = R ^{- 1} f ( l , θ ) = 1     d θ

2 π ^{2 0     -∞}

В данном случае под оператором R ^{- 1} понимается результат приближенного воздействия оператора обратного преобразования Радона.

Исходя из условия (9) понятно, что оптимальное расположение ракурсов проекций определяется, очевидно, выражением:

∂ p ( l , θ ) / ∂θ = max ,

где p ( l , θ ) – проекция, полученная под углом θ .

Следовательно, информационная отдача алгоритмов реконструкции зависит от выбора оптимальных углов между исходными ракурсами.

Для оценки спектрального разрешения доступных наборов проекционных данных целесообразно перейти в спектральную область Фурье. Так как мы имеем дело с дискретным набором проекций и дискретным количеством отсчётов в каждой из них, то необходимо переопределить искомые и проекционные данные в дискретном виде:

f_m ( x , y ) =

П М-1 Г    Г  п Y   . (  п)   п)

= p x cos m + y sin m , m .

м т - 0 (    ( М )     ( М )

Соответственно Фурье-спектр искомой функции:

π M-1

F (®x , ®у ) = X Р П (Юx cos(m) x y M m=0 m, π

π

+ω _y sin( m )). y M

Заметим, что два последних выражения записаны для декартовой сетки. В то же время, согласно теореме о центральном сечении, вычислив Фурье-спектры проекций и расположив их на Фурье плоскости в соответствии с ракурсами проецирования, можно синтезировать двумерный спектр Фурье, связанный со спектром искомой функции. Это справедливо в опре- делённом приближении и при условии, что набор спектров проекций, заданных на полярной сетке, умножен на некоторую двумерную функцию, соответствующую так называемому ρ – фильтру.

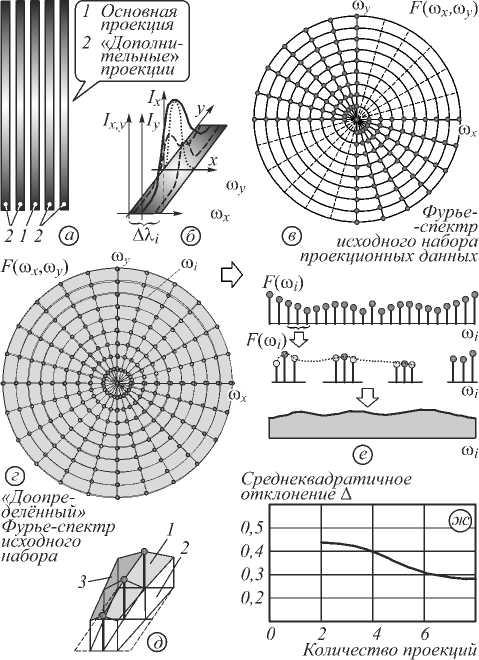
Рис. 2. Иллюстрация метода доопределения проекционных данных по кольцевым гармоникам

Имея спектры проекций (на полярной сетке), можно доопределить недостающие проекции, проводя интерполяции по кольцевым гармоникам. Эти процедуры подробно представлены на рис. 2. Из рис. 2 г ) понятно, что неточность реконструкции связана с потерей мелких деталей изображения, т.к. с ростом частоты «плотность полярных отсчётом» резко уменьшается.

Максимальную частоту дискретизации можно определить из задаваемого («желаемого») разрешения и элементарной геометрической интерпретации в Фурье-пространстве. Действительно, из равнобедренного треугольника, построенного на соседних лучах Фурье-спектров проекций (рис. 2 д) ), ограниченных «дугой» кольцевой гармоники заданной частоты следует условие:

∆ω _m = 2 ω _m sin( π /2 M ) . (13)

Для повышения точности восстановления можно предложить ряд методов вычисления «недостающих» проекций из экспериментальных данных. В этом плане возможными оказываются два варианта. Реально оптическое изображение каждой проекции регистрируется в виде «тонкой» двумерной функции, на которой можно выделить, например, 5 (см. рис. 2 а )

одномерных проекций, незначительно отличающихся друг от друга. Это обусловлено тем, что фактически регистрация производится вдоль главной оптической оси и двух побочных . Местоположение осей выбирается в плоскости, ортогональной плоскости исследуемого сечения. Полученные «побочные» проекционные данные обладают геометрически искажениями, которые можно компенсировать процедурой свёртки с известной аппаратной функцией.

С другой стороны, в системах такого типа количество отсчётов вдоль каждой проекции может быть достаточно большим (при использовании линейных матриц с высоким разрешением). Следовательно, если вычислить Фурье–спектр проекции и «расположить» его на 2D-Фурье–плоскости, то разумно ожидать, что на близко расположенных радиусах Фурье– плоскости по отношению к радиусу Фурье–образа данной проекции изменения участка Фурье поверхности будут аналогичными. Это обстоятельство и позволяет построить эти участки (см. рис. 2 д )). В совокупности с первым способом этот подход даёт возможность расширить углы конвергенции проекционных данных в Фурье–пространстве, между истинной проекцией и вычисленными – дополненными.

Существует ещё одна возможность, вытекающая из особенностей использования спектральнотомографической диагностики потоков ПИД. Действительно, при реконструкции искомых функций распределений мы имеем дело либо с набором «узких» участков физических , сплошных спектров , вблизи заданной длины волны( λ – ∆λ , λ , λ + ∆λ ), либо с набором спектральных линий. Тот и другой случаи соответствуют наборам исходных проекций. Распределение интенсивности вдоль спектральной линии – это есть проекционные данные для конкретной длины волны. Распределение интенсивности в ортогональном направлении – информация о функции распределения в близлежащем участке физического спектра. Её можно рассматривать как функции распределения близко расположенных проекций в заданном спектральном диапазоне ( физическом ) см. рис. 2 б . Действительно в данном спектральном приборе она оказывается полученной в близлежащих побочных оптических осях. Это позволяет в Фурье-пространстве вычислить дополнительные проекции рядом с исходными спектрами проекций.

Таким образом, в Фурье–пространстве после стандартной процедуры доопределения исходных данных во 2-м и 4-м квадрантах (рис. 2в-г), мы имеем дело не с одиночными радиусами отсчётов, а с «реперными наборами». Любой из них оказывается вблизи каждого «центрального» радиуса, а по обеим сторонам располагаются вычисленные, также «реальные» радиусы отсчётов дополнительных проекций (см. рис. 2е)). Это облегчает дальнейший процесс вычисления промежуточных проекций, позволяет более полно обосновать выбираемый алгоритм интерполяции, и повышает точность реконструкции в целом. С т.з. процедуры интерполяции задача сводится к вычислению по «кольцевым гармоникам» 1D Фурье–образов в «пустых» секторах плоскости ((π/M)–2k∆θ). Здесь k – количество «боковых» проекций в репере каждого ракурса. Определим кольцевые гармоники, как:

F ^{+ 1}( n ∆ω , m ∆ω ) = F ^{+ 1} _n ( m ∆ω ); ω= ω ² _x +ω ² _y . (14)

Следовательно, задача состоит в вычислении F ⁺¹ n ( m ∆ω ) в M – областях с «размером» (( π / M )–2 k ∆θ ) в интервале [0, π ]. Решение целесообразно выполнить с помощью хорошо известного метода наименьших квадратов с использованием в качестве базисных функций полиномов Чебышёва 1-го рода. Для этого необходимо определить минимум среднеквадратичного отклонения в заданных точках «кольцевых гармоник» [ 8 ] , то есть:

(2k+1)M +1

ρmin =    1      ∑ [F n(m∆θ) -F n(m∆ω)] ,(15)

(2 k + 1) M m =1

здесь:

₁                (2 k +1) M

F n(m∆θ) = ∑ CjTj-1(m∆θ) ,(16)

m -1

где T j –1 ( m ∆θ ) – полиномы Чебышёва 1-го рода. В этом случае частота дискретизации по сравнению с (13) возрастает:

∆ω _m = 2 ω _m sin( ∆θ / 2) .

Т.к. при малых углах sin α≈α в пространстве сигналов должно выполняться условие:

D /2 ≤ ( π / ∆θ ) = ( π / ∆θω _m )                   (18)

и с учётом того, что на полярной сетке с ростом частоты, плотность отсчётов уменьшается, ограничение по частоте в предельном случае определяется задаваемым разрешением: ∆l ≤ (π/ωm). Исходя из задаваемого разрешения, количество необходимых проекций – N с количеством отсчётов – n, в каждой из них, ис- пользуемых для процедуры реконструкции, может быть определено из выражения:

π ≥ ωmD = πn ∆θ 2     2 .

Отсюда несложно определить условие для углов конвергенции между ракурсами - реальных и вычисленных проекций, при заданном разрешении:

∆θ = ( ≤ ) 2( π ^{- 1}). (20)

С другой стороны, для выполнения последнего условия в рамках интерполяционной формулы (16) необходимо наложить дополнительное условие на количество основных и дополнительных ракурсов:

M =π ((2 k + 1) ∆θ ).

Другими словами, для условия (15) необходимо, для корректной процедуры интерполяции, иметь ( π∆θ ) кольцевых гармоник .

Используя информацию «боковых» проекций в каждом репере, по каждой кольцевой гармонике, применяя многочлены Лагранжа второй степени, как это сделано в работе [8], при мультималоракурсной системе регистрации данных, систему уравнений (16) можно доопределить. Для этого необходимо потребовать не только совпадения функций по кольцевым гармоникам с аппроксимирующими функциями, но и совпадение первой и второй производных при условии, что последние существуют, то есть:

1                 (2 к +1) M

{Fn}(mАО) = £ CjT]-i(mде), m-1

_ 1            (²^) M

H F n }'( m де ) = £ C ] m АО )]',        (22)

m ^{- 1}

_ 1                (2 к +1) M

{F.}"(mАО) = £ Cj[T]-1(mАО)]"- m-1

Систему уравнений (22) можно значительно упростить, принимая во внимание следующие обстоятельства. Коэффициенты C ] искать нет необходимости, так как согласно условию (19) достаточно определить 1

значения { F n }( m АО ) в «пропущенных» секторах , то есть для каждой «кольцевой» гармоники в областях (( п / M )-2 к АО ). В зависимости от номера гармоники количество слагаемых в линейной комбинации (16) можно снизить до n , т.е.:

F ¹ n ( m АО ) = ^ CT -A m АО ).                (23)

j =1

Способы решения систем уравнений типа (23) достаточно подробно изложены в монографии [9].

Выполнив процедуры интерполяции по каждой кольцевой гармонике, используя обратное одномерное преобразование Фурье, находим вычисленные промежуточные проекции:

n -1

P m АО ^{( к А 1} ) = ^АЮ / Z ^P m АО ⁽ n ^Аto i ) e^XP⁽ i ^{2 П} n ^А№ ! ^{к А 1} ) ^{. (24)} n =0

Для реконструкции искомой 2В-функции распределения производятся процедуры свёртки функций проекций с малоракурсным ядром типа (8).

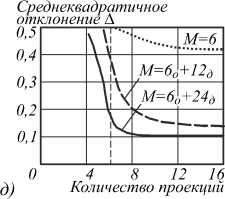
На рис. 3 а - г показаны этапы и результаты модельных экспериментов рассмотренного метода реконструкции при разном количестве основных и дополнительных проекций. Рис. 3 е) отображает обобщённые погрешности восстановления в зависимости от количества ракурсов ( M =6 о +12 д ,24 д ) (индекс « Д » здесь означает количество дополнительных проекций по отношению к главному ракурсу) в сравнении с восстановлением без учёта дополнительных проекций ( M = 6).

б)

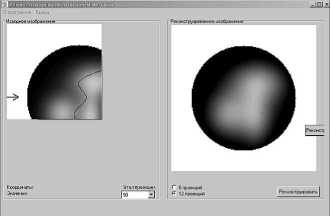
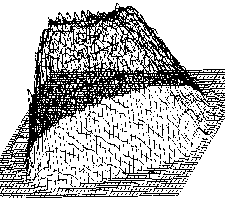
Рис. 3. Иллюстрации методов моделирования доопределения и представления данных

Томографический подход позволяет восстановить локальные значения в достаточно малых зонах сечения - по определению. Следовательно, разбив выбранное тонкое сечение факела на совокупность «трубок», можно предположить, что в каждом таком элементарном канале поле достаточно однородно. Поэтому для возбуждённых компонент типа лёгких ионов, электронов, распределение по скоростям может подчиняться распределению Максвелла. В возбуждённом состоянии распределение частиц в каждой элементарной трубке должно также подчиняться [ 4 ] формуле Больцмана

N s = N о ( g s / g о ) e ^{- ( 6} s / kT\ (25)

здесь N 0 , g 0 - концентрация и статистическая масса частиц для нормального состояния, N s , g s - концентрация и статистическая масса в возбуждённом состоянии. В соответствии со сделанными допущениями для каждого канала распределение атомов по стадиям ионизации можно рассчитать по формуле Саха [ 10 ] . Процессы ионизации в ИПД можно описать в виде системы уравнений, предложенной в работе [ 11 ] , куда входит степень ионизации отдельной компоненты x i . Результирующая ионизация может быть определена как [ 6 ] :

• x = = f zZ n i X i ) / \t". L                         (26)

V i =1       ) V i =1 /

Суммарное давление в анализируемом объёме, можно оценить из выражения [ 11 ] :

--p = aT ^3/2 e" kT — .

1 - x i 1 + x _z                 U ₀

Состояние исследуемого плазменного объекта в объёме элементарной трубки можно описать достаточно корректно, если электронная и ионная компоненты могут быть описаны с помощью: уравнения n состояния p = ^ NkT , распределения Максвелла -i=1

Больцмана, формулы Саха (в определённом приближении), формулы Планка.

В общем случае количество фотонов, излучаемых в каждом элементарном объёме, пропорционально: вероятности перехода – A_n ^m , атомов (ионов) из состояния n в состояние m , количеству атомов – n m , имеющих такие (возбуждённые) состояния m . Коэффициент излучения для данной линии спектра можно очевидно определить в виде соотношения: i ( к ) = (1/4 п ) A m n_mh v .

В выбранном направлении проектирования при заданных значениях ( r , 0 ) из элементарных объёмов вдоль хорды l можно сформировать плазменный цилиндр, приняв величину площади поперечного сечения A S = l и длинной l . Интенсивность излучения этого «плазменного цилиндра» в каждой точке проекции, при фиксированном значении угла 0 i , будет равна [ 8 ] :

J ( l ; 0 ; r ) = (1/4 п ) AXh v l .                      (28)

Для рассматриваемых задач интенсивность спектральной линии [ 11 ] можно определить, с учётом (28) как:

^Е m

J = (V4 n ) A> о ( g m) U 0 ¹ ) ) e ^kT h v l ,               (29)

здесь U 01 - статистическая сумма по возбуждённым состояниям, g m - статистический вес, Е m - энергия возбуждённого уровня m [ 11 ] :

h (v-v g )

• e ^kT a ,.

^E v

32 п ² e ⁶( Z + S )² N e N i З73 с ³(2 я m )^3/2 V kT

здесь Z – заряд иона до захвата электрона, S – заряд иона после захвата электрона, N e , N i – концентрация электронов, ионов. Следовательно, результирующая интенсивность в точке ( г , 0 ), очевидно, складывается и равна:

^Е m

J 0 = (14 п ) A ,m n о ( g m/ и 0 ¹ ) ) e" ^kT h v l + e _v l .

Таким образом, значение локальной температуры можно определить, используя (29) с учётом поправок (30), (31). При вычислении локальных значений температур наибольшую сложность составляет вычисление A_n ^m . Эта задача может быть разрешима, если воспользоваться эталонным источником излучения [ 9 ] (ленточные лампы, нити). Рассмотренная методика реконструкции T ( x , y ) с точки зрения спектроскопии соответствует методу абсолютных температур. Относительная погрешность описанного выше метода определяется выражением [ 8 ] :

^{A T} = ± ²³ kT ln[------ ^{1 + ( A} J / J ) ------].    (32)

^{T     Е} m      (1 -^{A N} )(1 -^{A l} )(1 -^A A m )

N l      A_n ^m

На рис. 4 приведена оптическая схема экспериментальной установки для спектрально-томографических методов определения локальных температур в заданном сечении ионного (плазменного) потока, определения абсолютной интенсивности факела и т.д. Система работает следующим образом. Макет плазменно-ионного двигателя располагается в вакуумной камере – 1. Объём камеры и производительность форвакуумного насоса и вакуумного насоса высокого разряжения выбираются исходя из условий эксперимента. При этом форвакуумный насос работает непрерывно, в течение всего хода эксперимента, удаляя продукты рабочего тела. Насос высокого разряжения подключается автоматически. В камере установлен макет двигателя и система сбора исходных 2D-проекционных данных, см. рис. 4 а ).

Автором разработан макет ИПД, который состоит из форсунки 1.1 (рис. 4 а )), через которую подаётся водород. Поток газа проходит модуль ионизации 1.2, в результате, за счёт воздействия переменного поля высокого напряжения поток ионизируется – появляются электронная и ионная компоненты. Электронная составляющая отводится отклоняющей системой (на рисунке не показана) от оси потока. Ионная компонента ускоряется простейшим линейным ускорителем 1.3, содержащим три каскада ускорения. Ускорение происходит в межэлектродных промежутках, причём ионный пучок дополнительно фокусируется.

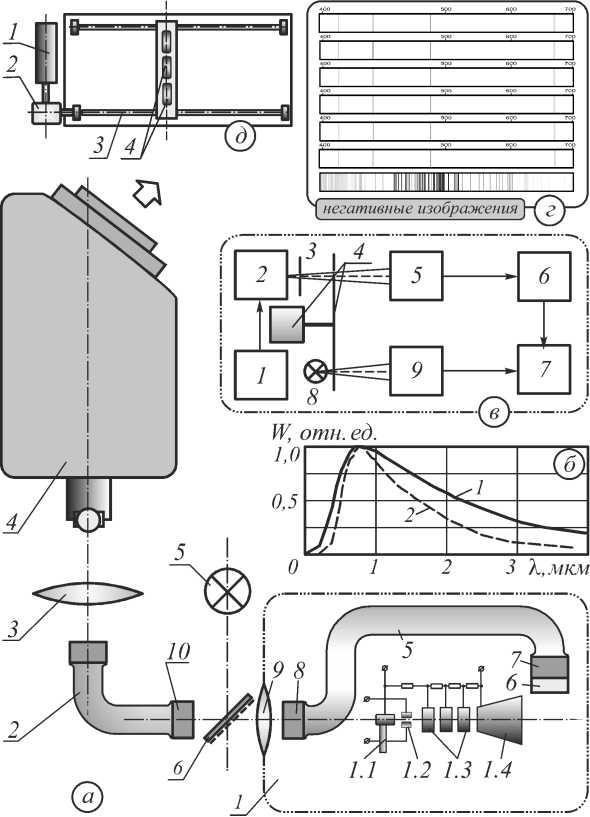
Рис. 4. Схема экспериментальной установки

Очевидно, что поток рабочего тела, выбрасываемый через сопло 1.4, содержит положительные ионы водорода, возбуждённые атомы и молекулы водорода. При этом атомы, ионы и молекулы водорода испытывают столкновения с молекулами остаточного газа в вакуумной камере, которые могут переходить в возбуждённые состояния. Таким образом, излучающими объектами в зоне регистрации являются атомы и молекулы водорода, возбуждённые атомы остаточного газа. Наличие остаточного газа надо учитывать при спектральном анализе, т.к. он проявляется в сплошном спектре, который накладывается на линейчатые спектры водородных ионов. В данной системе установлена ленточная лампа – 5 и полупрозрачное зеркало – 6. В фокальной зоне спектрографа формируется четыре (семь) спектра – 3 или 6 спектров проекций и один спектр ленточной лампы (рис. 4г)). На рис. 4в) приведена схема калибровки ленточной лампы, которая после этой процедуры становится эталонным источником излучения с определённым коэффициентом серости. Система калибровки ленточной лампы состоит из следующих блоков: 1 – стабилизированный источник питания 2 – вольфрамовая лампа, ленточного типа, 3 – диафрагма, 4 – дисковый модулятор, 5 – калибровочный детектор, 6 – усилитель, 7 – блоки обработки данных, 8, 9 – источник и детектор синхросигналов.

Оптико-волоконная система сбора проекционных данных частично также размещена в вакуумной камере, рис. 4 а ). Здесь же расположены двумерные коллиматоры – 6, светопроводы – 7. Для вывода 2D-проекционных изображений за пределы камеры применена оптическая развязка, содержащая проецирующий объектив – 9, который вмонтирован в боковую стенку камеры. Объектив проецирует изображение с выходных торцов светопроводов – 5 на входной торец светопровода – 2, находящегося вне вакуумной камеры. Далее изображения проекций передаются с помощью светопровода – 2 и линзы – 3 на щель спектрального прибора – 4. В данном эксперименте нами был использован спектрограф ИСП-30. В фокальной плоскости спектрографа формируются спектры проекций. При спектрально-томографической диагностике необходимо выбрать заданное сечение 3D- ионно-плазменного объекта. Это позволяет в этом 2D-сечении провести реконструкцию распределения локальных температур, концентраций ионной и электронной компонент и т.д.

Для считывания распределения интенсивностей вдоль спектральных линий применена электромеханическая система привода линейных ПЗС-матриц, рис. 4 д ). В данном случае использовано три линейных матрицы – 4, закреплённых на подвижной платформе. Она с помощью электродвигателя – 1 через редуктор – 2 и винтовые пары – 3 приводит в поступательное движение платформу с матрицами – 4.

Для реконструкции 3D-конфигурации искомых распределений при спектрально-томографическом способе исследования ионно-плазменных потоков разработана система формирования исходных данных, сущность которой можно пояснить с помощью рис. 5.

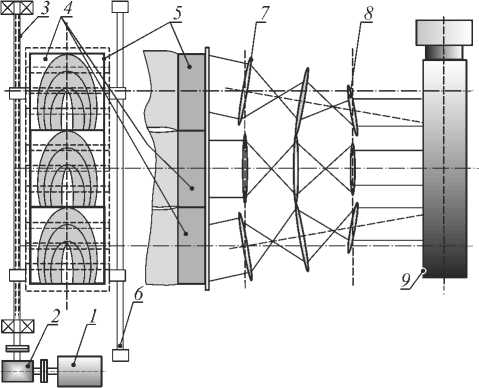
Рис. 5. Оптическая схема регистрации проекционных данных для восстановления 3D-конфигурации искомых распределений 1 – электродвигатель, 2 – редуктор, 3 – винтовая пара, 4 – многощелевая насадка, 5 – пакет светопроводов, 6 – направляющая, 7 – система проецирующих линз, 8 – корректирующие линзы, 9 – щель спектрального прибора

Собственное излучение плазменного потока фиксируется в трёх ракурсах, как это показано на рис. 5). Выходные торцы светопроводов собираются в параллельный пакет – рис. 5 позиция 5. Для выборки заданных сечений ортогональных оси потока используется насадка спектрографа – 4.

Так как плазменные и ионные потоки рассматриваемых ИПД обладают высокой осевой симметрией, то для реконструкции пространственной конфигурации искомых распределений выбирается три сечения в данном плазменном факеле. Конструкция привода многощелевой насадки позволяет с помощью электромеханической системы – 3 выбирать проекции сечений на заданных координатах оси факела. Привод состоит из винтовой пары – 3, связанной с многощелевой насадкой – 4, приводимой в движение электродвигателем – 1 и редуктором – 2. Направляющая – 6 служит для фиксации пространственного местоположения насадки относительно плоскости выходных торцов светопроводов. Выбранные проекционные изображения сечений с помощью системы линз – 7 и корректирующих линз Френеля – 8 проецируются на щель спектрального прибора – 9. В его фокальной плоскости, таким образом, формируется 9 изображений спектров проекций – 10, соответствующих трём выбранным сечениям. Для коррекции искажений, вызванных наклоном линз – 7, в качестве корректирующих предложено использовать линзы Френеля со «смещённым» оптическим центром [12]. 3D-реконструкция искомых функциональных распределений.

• 3. Программное обеспечение малоракурсных систем диагностики потоков ИПД

С учётом рассмотренных особенностей в качестве программного обеспечения для описываемого малоракурсного оптического томографа был создан ППП

(в последней модификации – «STAR»). Его обобщённая структурная схема представлена на рис. 6. Поясним основные функции отдельных модулей и их взаимосвязь между собой. Блок управления определяет режимы системы электропривода и процессы сканирования в ПЗС-детекторах. Этот модуль через устройства ввода-вывода связан с ПК, с помощью которого задаются координаты местоположения ПЗС-матриц, определяется момент начала опроса, его длительность.

Так как объем исходных проекционных данных достаточно велик, а время опроса каждой матрица составляет - 1 - 10 -3 с и менее, то прямой ввод данных зачастую невозможен, поэтому в системе предусмотрены промежуточные буферы накопления. Они обслуживают модуль получения и формирования исходных данных. Для выбора оптимального алгоритма реконструкции необходимо проанализировать характер проекционных данных. Для этого, по виду 1D-функций проекций, выбираются процедуры доопределения отсчётов, вычисления промежуточных проекций, вид модельной функции. С помощью модуля синтеза цифровой модели можно построить 2D-модель реконструкции или 2D-сечения. Далее производится моделирование полного цикла реконструкции. В результате уточняются параметры доопределения исходных данных, вид фильтрующих функций, параметры FT-операций, форматы реконструкции.

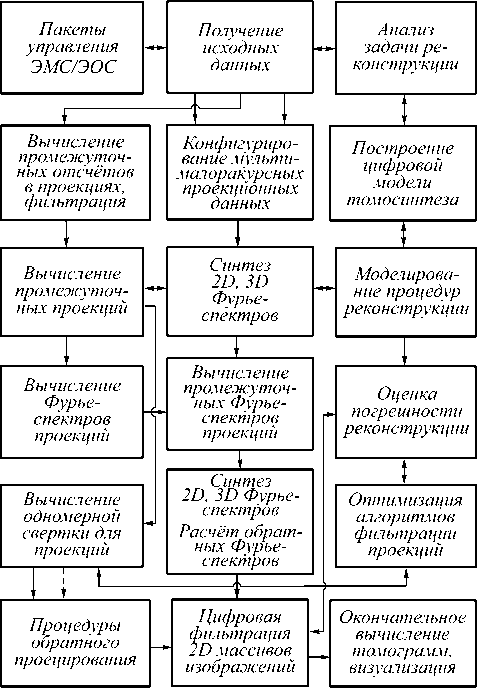
Рис. 6. Схема ППП «STAR»

Модуль для оценки погрешностей МВТ-рекон-струкции даёт возможность рассчитать погрешности основных процедур восстановления. Модуль оптимизации алгоритмов фильтрации даёт возможность ускорить процедуры вычисления операций типа свёртки, при различных форматах исходных данных, при вычислении 1D FT. С помощью данного модуля выбирается наиболее оптимальный алгоритм вычисления исходя из соображений точности и быстродействия. Модуль визуализации подготавливает изображения сечений в необходимом формате позволяет преобразовать чёрно-белый вариант в цветную форму, выделить изо- линии, представить их в виде проекционного или стереоскопического изображения.

На рис. 7 показаны внешний вид малоракурсной лабораторной томографической установки для исследования ионно-плазменных потоков (атмосферный вариант) (рис. 7а), а также примеры полученных с её помощью восстановленных томографических изображений. Данная система позволяет полу- чать до 24 ракурсов в пределах (0^2л). На рис. 7б приведены: модельная функция для многопотоковых ИПД (левый верхний угол изображения), и результат восстановления (модельный эксперимент) проекционных данных с помощью свёрточного алгоритма (правый нижний угол).

а)

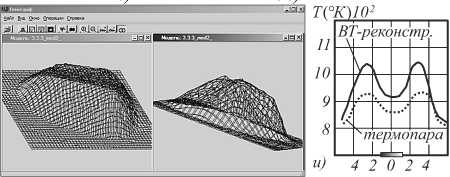
Рис. 7. Внешний вид 24-ракурсного оптического томографа для лабораторных исследований, примеры реконструированных изображений и способы отображения

д)

б)

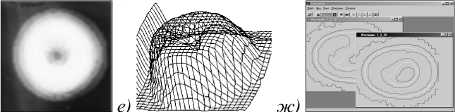
На рис. 7 в показаны спектры 12 проекций, формирующиеся в зоне считывания данных спектрографа. Блок считывания хорошо виден на заднем плане (фокальная зона спектрографа). Идентичные спектральные линии при рассматриваемом способе регистрации должны находиться на одной вертикальной прямой (см. линия Ar ^Х = 4627 нм). Рис. 7 г-е отображают способы представления восстанавливаемых функциональных распределений, в данном случае локальных температур, соответственно в виде полутоновых изображений и в проекционном виде. На рис. 7 ж-з приведены примеры отображения реконструированных функциональных распределений в виде семейств изопара-метрических кривых и в виде стереоскопического проекционного изображения. На рис. 7 и показан температурный профиль вдоль заданного диаметра потока.

Заключение

Разработаны методы и средства для малоракурсной томографической диагностики параметров ионных и плазменных потоков ИПД по собственному излучению в оптическом диапазоне. Методы 2D-реконструкции искомых функциональных распределений, таких как локальные значения интенсивностей, температур и пр., позволяют в свёрточном приближении обращения Радона восстанавливать искомые распределения при числе исходных проекций от 3 до 24.

Алгоритмы и соответствующие ППП ориентированы на стандартные ПК при восстановлении 2D-распределений и на кластерные системы [ 15 ] при решении трёхмерных задач. Форматы реконструкции могут быть выбраны в пределах от (128 x 128) до (512 x 512) элементов. В алгоритмах реконструкции, за исключением процедур обратного проецирования, используются только одномерные процедуры вычислений таких операций, как прямое и обратное преобразование Фурье, свёртка.

Погрешности восстановления искомых функциональных распределений находятся в пределах от (5 ^ 7)% до (10 ^ 12) %. Оценка погрешностей производилась по отклонениям заданных модельных функций и реконструированных распределений.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках гос. задания № 9.1421.2014/K.