Методы имитационного математического моделирования российского срочного рынка на современном этапе

УДК 05.13.18                                              

2Russian Customs Academy, Rostov Branch, Rostov-on-Don, Russian Federation

Введение. Работа посвящена имитационному моделированию. Описаны основные методы имитационного математического моделирования на срочном рынке. Рассмотрена группа реалистичных негауссовских процессов Леви, которые обобщают классическую модель Блэка-Шоулса. Целью работы явилось исследование наиболее эффективных методов прогнозирования рынка, а также программная реализация метода имитационного математического моделирования российского срочного рынка, основанного на модели Леви. Данное исследование актуально в связи со спросом на приложения, позволяющие симулировать динамику финансовых активов и оценивать опционы в реалистичных моделях срочного рынка, допускающих скачки.

Материалы и методы. Рассмотрены основные методы прогнозирования срочного рынка, способы определения уровня волатильности при известной цене опциона. Выделены наиболее эффективные виды процессов Леви для имитационного математического моделирования российского срочного рынка на современном этапе. Рассмотрены возможности языка Java для реализации математических методов.

Результаты исследования. Разработана программа на языке Java , реализующая математическую модель Леви, включающую в себя гауссовский и обобщённый пуассоновский процессы. Программа для реализации математического метода создана в свободной интегрированной среде разработки приложений NetBeans IDE для работы с любой операционной системой.

Обсуждение и заключения. В результате анализа имитационного математического моделирования на срочном рынке наиболее эффективными являются методы, основанные на реалистичных негауссовских процессах Леви. Программная реализация таких математических методов может использоваться в учебных целях. Разработанное приложение показало высокое качество и скорость расчётов с помощью программных ресурсов.

Introduction. The paper is devoted to simulation modeling. Basic methods of the simulation mathematical modeling in the derivatives market are described. A group of realistic nonGaussian Levy processes that generalize the classical Black-Scholes model is considered. The work objective is to study the most efficient methods of market forecasting, as well as the software implementation of the simulation mathematical modeling technique of the Russian derivatives market based on the Levy model. This research is relevant due to the demand for applications that simulate the dynamics of financial assets and evaluate options in realistic models of the derivatives market, allowing for jumps.

Materials and Methods . Basic methods for forecasting the derivatives market, methods for determining the volatility rate at a known option price, are considered. The most effective types of Levy processes for the simulation mathematical modeling of the Russian derivatives market at the present stage are highlighted. The possibilities of the Java language for the implementation of mathematical methods are considered.

Research Results. A program is developed in the Java programming language that implements the Levy mathematical model, which includes Gaussian and generalized Poisson processes. The program for calculating the mathematical method is created in the free integrated application development environment NetBeans IDE to work with any operating system.

Discussion and Conclusions. The result of the simulation mathematical modeling analysis has shown that the most efficient methods in the derivatives market are those based on realistic non-Gaussian Levy processes. The software implementation of such mathematical methods can be used for educational purposes. The developed application has demonstrated high quality and speed of calculations using software resources.

Леви, классическая модель Блэка-Шоулса, срочный ры-      model, derivatives market, Gaussian process, generalized нок, гауссовский процесс, обобщённый пуассоновский     Poisson process.

процесс.

Образец для цитирования: Карпинская, Т. А Методы      For citation: T. A. Karpinskaya, et al. Methods of simulation имитационного математического моделирования россий-      mathematical modeling of the Russian derivatives market in ского срочного рынка на современном этапе /      modern times. Vestnik of DSTU, 2019, vol. 19, no. 4, pp. 398 -

Т. А. Карпинская, О. Е. Кудрявцев // Вестник Донского      406. /10.23947/1992-5980-2019-19-4-398-406

гос. техн. ун-та. — 2019. — Т. 19, № 4. — С. 398 -406. /10.23947/1992-5980-2019-19-4-398-406

Введение. Современная рыночная экономика не способна существовать без эффективной работы финансового рынка. Здесь особое место занимает рынок срочных финансовых инструментов, позволяющий хеджировать риски нежелательного скачкообразного изменения цен на фондовом или валютном рынках. Российский срочный рынок активно развивается, привлекая все больше инвесторов. В этой связи растет спрос на программные средства, позволяющие симулировать динамику финансовых активов и оценивать опционы в реалистичных моделях, допускающих скачки в ценах.

Явным или неявным образом, обрабатывая входящую информацию, каждый из участников рынка может прогнозировать будущие движения цен. То есть торговая система ― это алгоритм преобразования различной информации в прогноз с определенными уровнями доверия. Системный трейдер поручает прогнозирование алгоритму, дискреционный/интуитивный трейдер использует свой опыт/интуицию. Из-за того, что любой прогноз имеет вероятностную природу, часть прогнозов не сбывается. Хороший прогноз должен быть обоснованным с точки зрения статистики, быть репрезентативным и должен использовать некие вероятности, закономерности, причинно-следственные связи. Идея, лежащая в основе прогноза должна быть рациональна и объяснима.

Адекватное моделирование срочного рынка позволяет участникам извлекать прибыль. Таким образом, исследование методов имитационного математического моделирования российского срочного рынка является актуальным, поскольку позволяет решать задачу определения адекватной стоимости срочного контракта. Новизна работы заключается в программной реализации имитационного моделирования вычисления цен опционов в модели Мертона на языке Java . В настоящее время особый интерес представляют приложения с web -интерфейсом. Язык Java ― естественный язык для решения данной задачи.

Материалы и методы. В первую очередь необходимо рассмотреть наиболее часто встречающиеся методы прогнозирования поведения срочного рынка. Методика исследования основана на изучении различных методов моделирования российского срочного рынка и выделении наиболее эффективного из них. К основным методам прогнозирования рынка относят:

• •    статистические;

• •    интуитивные;

• •    основанные на моделировании;

• •    экспертные.

Технический анализ ― это метод прогнозирования вероятного изменения цен на основе закономерностей, представленных в виде аналогичных изменений цен в прошлом в схожих обстоятельствах. То есть можно утверждать, что технический анализ использует статистические методы и некие модели. Объектами прогнозирования могут быть различные рыночные характеристики: направление приращений, приращения, волатильность, трендовость и т. д. Объект прогнозирования зависит от идеи, с помощью которой трейдер намерен извлекать прибыль из рынка. Большинство процессов на срочном рынке стохастические, то есть их поведение не является детерминированным. Последующее состояние рынка можно описывать как величинами, которые могут быть предсказаны, так и случайными величинами [1]. Например, использование сантимента или паттернов предполагает прогнозирование направления и волатильности, а использование маркетмейкинга предполагает прогнозирование волатильности и ее тайминга.

На срочном рынке помимо валюты существует возможность торговли ценными бумагами и металлами. Проводя операции с российскими ценными бумагами, необходимо помнить, что цены на них постоянно меняются, и важно угадать правильный момент для их покупки и продажи. В этом и есть особенность операции с российскими ценными бумагами.

Информатика, вычислительная техника и управление

В связи с нестабильностью экономики многих стран, в том числе России, существует большая возможность заключить невыгодную сделку. На срочном рынке есть понятие индекса относительной силы ( RSI) , с помощью которого можно определить доход от сделки [2]. Для расчета скорости роста дохода предприятия можно использовать метод Тома Демарка, который является довольно действенным для технического анализа ситуации на срочном рынке. При колебаниях рынка для вычисления спреда в случае скупки акций важными будут основополагающие свойства деформированных мартингалов, так как наилучшим прогнозом поведения рынка в таких случаях является изучение его состояния в данный момент [3]. Рынок ценных бумаг России и США не одинаков и при анализе дохода на российском рынке может получиться нулевой результат по отношению к американскому образцу. Это происходит из-за того, что проданные бумаги на российском рынке через несколько минут могут потерять свою ценность, в отличие от американского рынка, где установленный курс на бумаги держится довольно долго. Такая тенденция свидетельствует о стабильности компании и желании остаться как можно дольше на мировом рынке валюты. Но здесь необходимо учитывать вес российского валютного рынка в мировых валютных отношениях [4].

Одно из главных направлений получения дохода на бирже — определение развития курса валют. Каждый биржевик стремится разработать собственный метод прогноза и применить его на практике. На бирже много пригодных для расчета индикаторов, но один из самых распространенных — расчет скользящего среднего. Согласно этому методу расчет проводится за определенный период, при этом вычисляют самые простые реализованные сделки, затем при пересечении индикатора с текущим курсом сделка заключается. Метод достаточно надежен, но требует непрерывного контроля. Чтобы проще было проследить изменение курса валюты, следует применять этот метод для коротких промежутков времени [5].

Существует понятие оценки взвешенного скользящего среднего, с помощью которого отслеживают данные за последнее время, при этом индикатор сглаживает колебание курса. Эта стратегия похожа на предыдущую и данные, полученные при ее использовании, близки к данным, полученным при использовании расчета скользящего среднего. Преимущество этого метода в том, что нужно отслеживать тренды только за последнее время.

Следующий метод — это метод экспоненциального скользящего среднего. При его использовании сравнивают данные за последнее время и данные за более ранний период. Этот метод вычисляет меньше прибыльных сделок, но при этом все сделки совершаются без риска убыточности.

Прогнозирование цен возможно, но лишь в том случае, когда есть связь между их прошлыми значениями и будущими. Эта связь действительно может наблюдаться во время трендов. Трейдеры, наблюдая за однонаправленным изменением цен, реагируют соответствующим образом и заключают сделки в направлении тенденции, создавая положительную связь между изменениями в прошлом и в будущем. Когда рынок растет без коррекций или растет в канале, основная масса спекулянтов осознанно покупает, рассчитывая на продолжение, и самим фактом покупок обеспечивает дальнейший рост. Тренд существует до тех пор, пока основная масса трейдеров, создающих тренд, не начинает фиксировать прибыль. Важным моментом для продолжения тренда является отсутствие контртрендовой торговли, то есть не должно быть слишком массивного давления рыночными ордерами в противоположную сторону. Если видимая структура тренда будет нарушена, то это может повлиять на спекулянтов, создававших своими сделками этот тренд, что приведет к фиксации прибыли и остановке тренда.

Результаты исследования. Среди существующих методов математического моделирования и анализа финансовых рынков в контексте российского срочного рынка в первую очередь необходимо отметить группу реалистичных негауссовских процессов Леви, которые обобщают классическую модель Блэка-Шоулса. Преимуществом данной группы процессов является возможность моделирования скачков цены базового актива и более реальная оценка рисков. Таким образом, методы математического моделирования и анализа финансовых рынков опираются на процессы Леви с постоянной, локальной и случайной диффузионной компонентой. Также существуют модели, имеющие стохастическую волатильность. Таковыми являются модели Хестона, Бейтса и Блашера [6].

Модель ценообразования Блэка-Шоулса определяет теоретическую цену на европейские опционы. Она подразумевает, что если базовый актив торгуется на рынке, то цена опциона на него неявным образом устанавливается самим рынком [7]. Модель получила широкое распространение и может использоваться на практике для анализа финансовых рынков, в том числе срочного. Согласно данной модели, основным элементом определения стоимости опциона является ожидаемая волатильность базового актива. Таким образом, при известной стоимости опциона можно определить уровень волатильности, ожидаемый рынком [8].

Текущая стоимость европейского опциона call C(S,t) в момент t до истечения его срока соответствует выражениям:

C(S, t) — SN(dl) — Ke-T(T-t N(d2), ln (K) + (r + T)(T — t)

dl —

;

oyT — t

d2 — dl — o ^(T — t), где S ― текущая цена базисной акции; N(x) ― функция стандартного нормального распределения; K ― цена исполнения опциона; r ― безрисковая процентная ставка; (T – t) ― время до истечения срока опциона (период опциона); σ ― волатильность доходности (квадратный корень из дисперсии) базисной акции.

Цена европейского опциона put соответствует выражению:

P(S, t) — Ke ^-r(r-t)_J! V(—d2) — SN(-dl).

Случайный процесс Х = ( Xt ) t ≥ 0, заданный на вероятностном пространстве (Ω, F , P ) и принимающий значения в d -мерном евклидовом пространстве R d 1, называется d -мерным процессом Леви при выполнении следующих условий:

• 1.    Процесс состоит из траекторий, принадлежащих определённому пространству D ᵈ , состоящему из векторных функций, является непрерывным справа и имеет пределы слева.

• 2.    Для любого n ≥ 1 и набора 0 ≤ t 0 <  t 1 < … < tn величины Х t 0, Xt 1– Xt 0, … , Xtn – Xtn –1 являются независимыми.

• 3.    Процесс однороден по времени. Для любых s ≥ 0 и t ≥ 0:

• 4.    Процесс стохастически непрерывен. Для каждого t ≥ 0 и ɛ > 0:

• 5.    Х 0 = 0.

Xt + s - Xs — Xt - X0.

Um P(\Xs - Xt| > e) — 0, s - t.

Процессы в случае конечной меры Леви:

• •    гауссовский;

• •    обобщённый пуассоновский;

• •   модель Мертона;

• •   модель Коу.

Процессы Леви с бесконечным количеством скачков в любой промежуток времени имеют меру Леви Π, обладающую свойством Π( R ) = ∞. Такие процессы активно используются при моделировании финансовых рынков. Здесь можно выделить:

• •   variance gamma (VGP);

• •   гиперболические (HP);

• •   обобщённые гиперболические (GHP);

• •   нормальные обратные гауссовские (NIG);

• •   нормальные умеренно стабильные (NTS);

• •   процессы KoBoL или CGMY.

Процессы Леви позволяют моделировать динамику цен активов максимально гибко, так как содержат две составляющие: броуновское движение (диффузия процесса) и скачкообразный компонент [9]. В настоящее время существует множество моделей, основанных на процессах Леви, которые успешно оперируют динамикой цен различных активов и используются при ценообразовании опционов, так как являются мартингалами. Декомпозиция Леви-Ито разбивает процессы Леви на простые составляющие и помогает понять их природу. Такая декомпозиция является основой для моделирования процессов Леви при помощи суммы двух составляющих: броуновского движения и составного процесса Пуассона. Такая структура стохастического процесса называется скачкообразной диффузией и имеет вид [10]:

Xt — yt + oBt + £^1 Yi, где Bt ― броуновское движение; Nt ― процесс Пуассона, считающий количество скачков процесса X к моменту времени t; Yi ― независимые одинаково распределённые случайные величины скачков.

Двумя крайними примерами случая конечной меры Леви являются гауссовский и обобщённый пуассоновский процессы. Если процессы Леви комбинируют в себе оба упомянутых процесса, то они называются дуффузией со скачками. Наиболее интересными моделями такого вида являются модель Мертона и модель Коу [10]. Для ускорения расчётов и обеспечения наглядности авторы разработали приложение на языке программирования Java , позволяющее реализовать данные модели.

Информатика, вычислительная техника и управление

В языке Java весь код хранится в виде классов. Таким образом, набирая исходный файл с расширением java , он компилируется в новый файл с байт-кодом. За счёт того, что Java спроектирован для выполнения байткода, программы, написанные на данном языке, работают с довольно высокой скоростью [11].

Весь расчёт при компиляции будет состоять из нескольких java -файлов. В одном из них проведём вычисления процесса Леви с прыжками. Этот файл будет осуществлять итоговое вычисление из всех остальных файлов. В одном из java -файлов проведем реализацию формулы Блэка-Шоулза (листинг 1), которая будет необходима в дальнейшем.

Листинг 1: реализация формулы Блэка-Шоулза public static double normcdf(double z){ if (z <=-7.0)

return 0.0; else if (z >=7.0)

return 1.0; else { double pi = 3.141592653589793;

double b1 = -0.0004406;

double b2 =  0.0418198;

double b3 =  0.9;

return 1.0 / (1.0 + exp(-sqrt(pi)*(b1*pow(z,5.0) + b2*pow(z,3.0) + b3*z)));

} } // Black Scholes call or put price public static double BSPrice(double S,double K,double r,double q,double v,double T,char PutCall) { double d1 = (log(S/K) + (r-q+v*v/2.0)*T)/v/sqrt(T); double d2 = d1 - v*sqrt(T);

double BSCall = S*exp(-q*T)*normcdf(d1) - K*exp(-r*T)*normcdf(d2); if (PutCall=='C') return BSCall; else return BSCall - S*exp(-q*T) + K*exp(-r*T);

} }

В двух других java -файлах рассчитаем абстрактный процесс, который описывает генерацию последовательности цен ко времени. То есть в одном java -файле высчитывается явная формула цены опциона, которая учитывает начальную цену, тренд и волатильность (формулы для расчёта цен опционов C(S,t) и P(S, t) приведены выше), в другом java -файле происходит симуляция по модели Мертона скачковой диффузии. Формула скачкообразной диффузии учитывает, что скачки будут нормально распределёнными.

Разработав интерфейс программы, после компиляции получим приложение для быстрого и удобного расчёта на основе генерации случайных чисел. Аналогично набор данных генерируется при каждом запуске (рис.1, 2).

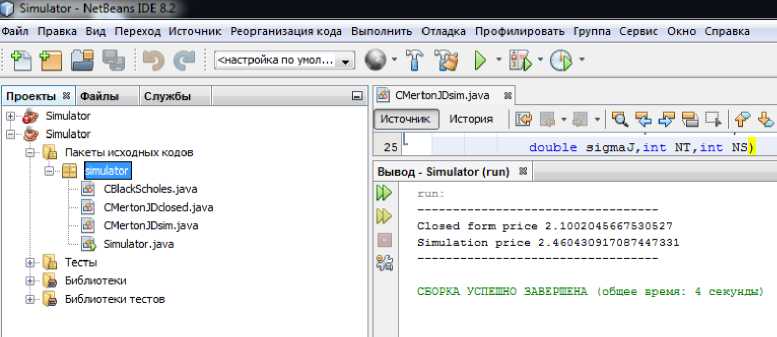
Рис. 1. Первый запуск программы

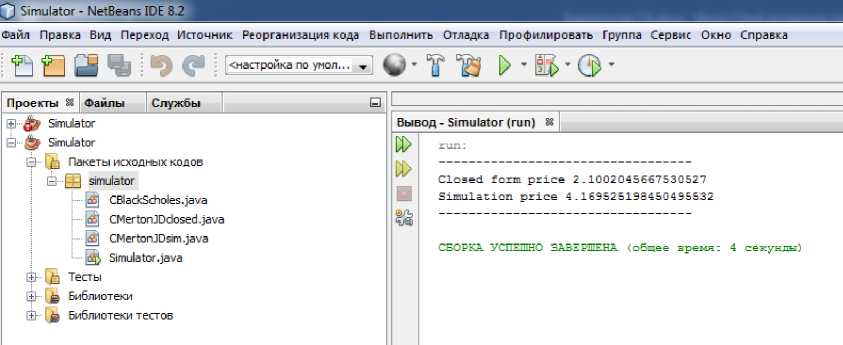
Рис. 2. Второй запуск программы

При первом запуске программы цена симуляции была значительно ближе к явной формуле цены опциона. Таким образом, во втором случае можно было продать опцион более выгодно, чем в первом случае. Проведя вычисления программы большое количество раз, можно спрогнозировать другие варианты для покупки или продажи опциона. Здесь необходимо учитывать все возможные факторы, способные повлиять на рынок. Проведём десятикратный запуск программы, результаты вычисления которого представлены в табл.1.

Таблица 1

Результаты десятикратного запуска программы

№ п/п	Closed form price	Simulation price
1	2.1002045667530527	2.460430917087447331
2	2.1002045667530527	4.169525198450495532
3	2.1002045667530527	2.472669282703422532
4	2.1002045667530527	1.065976524175292432
5	2.1002045667530527	1.119330912080574833
6	2.1002045667530527	2.687540413685037333
7	2.1002045667530527	1.184835796571303834
8	2.1002045667530527	4.53211404384426131
9	2.1002045667530527	8.00388383946741132
10	2.1002045667530527	1.685687889204974432

Симуляция показывает возможные варианты развития событий на срочном рынке и позволяет оценить убытки. Соответственно, продавать опцион наиболее выгодно в девятом случае при Simulation price , равной 8.00388383946741132. Исходя из данного прогноза, владелец опциона может получить наибольший доход от сделки. Для покупки опциона наилучший прогноз имеет место в четвертом случае при Simulation price , равной 1.065976524175292432. Таким образом, Closed form price является идеальной ценой, а Simulation price ― это цена, которую выставляет рынок, которая учитывает его изменчивость и скачки. Таким образом, можно распределять свои лимиты на рынке, предсказывая размер убытков и доходов.

Сначала рассчитывается явная формула цены опциона (настоящая цена) Closed form price (листинг 2). Она даёт математическое ожидание выплаты по опциону, то есть учитывает все возможные варианты развития событий. Далее запишем необходимые нам ячейки для реализации формулы.

Листинг 2: явная формула цены опциона

{     // Expected jump value double kappa = exp(muJ + 0.5*sigmaJ*sigmaJ) -1.0;

// Initialize the price double Price =0.0;

double sigman,rn,BSPrice,lambda,Probability;

for (int n=0; n

rn = r - lambdaJ*kappa + n*log(1.0+kappa)/T;

BSPrice = CBlackScholes.BSPrice(S0,K,rn,q,sigman,T,PutCall);

Информатика, вычислительная техника и управление

lambda = lambdaJ*(1.0+kappa);

Probability = exp(-lambda*T) * pow(lambda*T,(double)n)/factorial(n); Price = Price + Probability*BSPrice;

} return Price;

}

После этого в программе реализуется симуляция мертоновской скачковой диффузии (листинг 3). Simulation price характеризует цену опциона, зависящую от некоторой имитационной траектории. Методы генерации чисел для абстрактного процесса содержатся непосредственно в файлах с реализуемыми процессами как, например, при расчете явной формулы цены опциона. Для реализации скачков рынка используем генератор случайных чисел.

Листинг 3: симуляция мертоновской скачковой диффузии public class CMertonJDsim { public static double JDsim(char PutCall,double S0,double K,double rf, double q,double sigma,double T, double lambdaJ,double muJ, double sigmaJ,int NT,int NS)

{     // Time increment double dt = T/NT;

// Random number generator and set the seed

Random rng = new Random();

// Define the distributions double poissrnd = poissonRandomNumber(lambdaJ*dt);

double N01 = normalDestribution(0.0,1.0);

double Nus = normalDestribution(muJ - 0.5*sigmaJ*sigmaJ,sigmaJ);

// Expected value of k, and drift term double kappa = exp(muJ) -1.0;

double drift = rf - q - lambdaJ*kappa - 0.5*sigma*sigma;

// Initialize the stock price paths and the payoff double Payoff =0;

//vector > S (NT,vector (NS)); double[][] S = new double[NT][NS];

// Perform the simulation for (int s=0; s

S[0][s] =S0;

for (int t=1; t

if (lambdaJ != 0.0){ int Nt = (int) poissonRandomNumber(rng.nextGaussian());

if (Nt >0)

for (int i=0; i

J += (int) normalDestribution(0,1);

} double Z = normalDestribution(0,1);

S[t][s] = S[t-1][s]*exp(drift*dt + sigma*sqrt(dt)*Z +J);

}

// Calculate the payoffs if (PutCall =='C')

Payoff = Payoff + max(S[NT-1][s] - K, 0.0);

else if (PutCall =='P')

Payoff = Payoff + max(K - S[NT-1][s],0.0);

} return exp(-rf*T)*(Payoff/NS);

int k =0;

double p =1;

do { k = k +1;

p = p *u;

} while (p >L);

return k -1;

} static double normalDestribution(double s, double m) { // create random object Random rand = new Random();

// generating integer double nxt = rand.nextGaussian();

return nxt * s + m;

}

}

Проведя симуляцию несколько раз, из полученных Simulation price можно выбрать среднее значение, которое проиллюстрирует скачки цены опционов. В итоге, чем ближе значение Closed form price к одному из значений Simulation price, тем более выгодна цена для покупки опционов.

Обсуждение и заключения. Практическим результатом исследования является разработанное приложение, имитирующее скачки рынка и реализующее сложную математическую формулу. Рассмотренная модель процессов Леви, включающих в себя гауссовский и обобщённый пуассоновский процессы, является эффективным методом вычисления важнейших характеристик финансового риска. Она позволяет принимать решения о реализации той или иной торговой стратегии с использованием контрактов на Московской бирже. Результаты исследования свидетельствуют о том, что выбранная для разработки приложения модель скачковой диффузии Мертона является эффективным методом математического моделирования. Данное приложение можно использовать для обучения персонала на рынках с биржевыми рисками. Проведённые расчёты показывают цену, которую выставляет рынок. Она учитывает все возможные варианты развития событий, а также возможные изменения цены опциона, согласно которым можно определить прибыль или убытки. Участник срочного рынка с помощью такого расчёта может принять наиболее выгодное решение для покупки опциона, если симуляция покажет цену ниже установленной рынком, либо для продажи, когда цена симуляции будет наиболее высока.

Установлено, что язык программирования Java может эффективно применяться при создании качественных приложений для расчетов на биржах, позволяет уменьшить время математических расчетов и упрощает работу с биржевыми вычислениями. При этом Java Virtual Machine является аналогом виртуального компьютера, расположенного в оперативной памяти и интерпретирующего байт-код. Все действия Java-программы замкнуты внутри данного виртуального компьютера таким образом, что имеется возможность не допускать их деструктивных действий.