Методы исследования структуры пылевого облака

Как известно, для исследования структурных особенностей пылевой плазмы применяются методы коллоидной химии [2], [4]. Эти методы позволяют оценивать степень упорядоченности частиц в отдельном сечении структуры.

Размер частиц – 1 мкм. Вещество частиц – LiNbO 3 . Разряд постоянного тока в смеси 3:1 Ne - H 2 , давление P = 1,3 Торр, I = 0,9 A, горизонтальный размер – 7 мм.

Для этого служат автокорреляционные функции, оценивающие степень трансляционной и ориентационной упорядоченности в структуре. Трансляционный порядок оценивается по средней плотности упаковки частиц в зависимости от расстояния до выделенной частицы.

Ориентационная упорядоченность определяется по среднему отклонению ориентации линий, соединяющих соседние частицы, от ожидаемой для того или иного типа упаковки. Параметры аппроксимации полученных для структуры функций позволяют произвести классификацию структуры в соответствии с имеющейся теорией двумерного плавления KTHNY [3], [4]. В случае ориентационной автокорреляционной функции таким параметром аппроксимации является показатель степени огибающей экспоненты. Для ориентационной корреляционной функции это параметры степенной или экспоненциальной аппроксимаций.

Рис. 1. Фотография горизонтального сечения середины плазменно-пылевой структуры

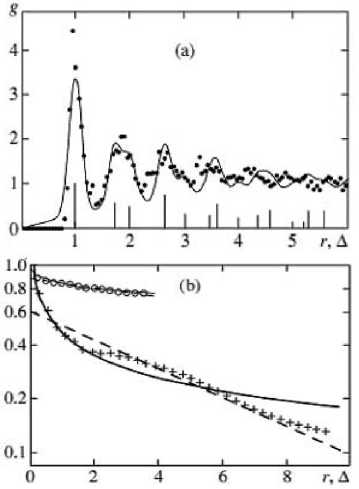
Рис. 2. (a) – парная корреляционная функция g(r); (b) – функция корреляции ориентации «связей» g6(r). «+» – g6(r) для всей структуры, «о» – g6(r) для домена с наибольшей упорядоченностью

Функции построены для сечения структуры, изображенной на рис. 1.

Для определения неоднородностей в сечении пылевого облака используют локальные трансляционный и ориентационный параметры [1]. На изображение сечения структуры накладывается карта значений параметров, на которой яркостью области обозначены значения этих параметров. Рис. 1–3 иллюстрируют применение нами корреляционных методов для определения состояния структуры по координатам частиц в двумерном горизонтальном сечении.

Светлые области – домены гексагональной упаковки.

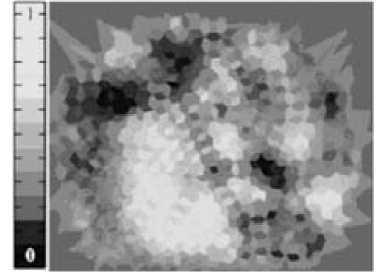
Рис. 3. Карта ориентационного корреляционного параметра g6(0) для структуры, показанной на рис. 1

Для изучения структуры трехмерного объекта возможно обобщение применяемых в плоском случае приемов. В частности, в случае трансляционной автокорреляционной функции удается сделать построение по прямой аналогии с плоским случаем.

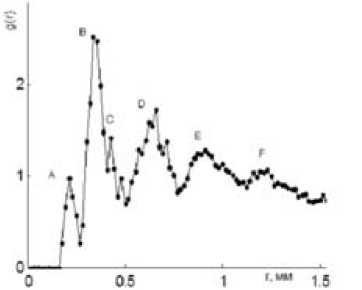
Рис. 4. Парная корреляционная функция для трехмерного объекта

Операция определения плотности частиц в кольце, описанном около выделенной частицы, в зависимости от радиуса кольца изменяется несущественно. Теперь около выделенной частицы описываются концентрические сферы. Определяется плотность попадающих в сферический слой частиц, и полученная зависимость плотности от радиуса усредняется по всем частицам структуры. Результатом этой операции становится трехмерная функция g(r) (рис. 4).

Для определения свойств структуры по полученной функции необходимо создать эталонную корреляционную функцию, построенную по модельной решетке с фиксированным типом упаковки частиц. Сравнение с такой функцией и даст возможность диагностики.

Для выстраивания модельной упаковки необходимо учесть основные параметры структуры. Их можно определить из имеющегося массива координат ее частиц. Это среднее межчастичное расстояние, наличие анизотропии и тому подобные основные особенности структуры.

Например, для многослойной структуры, полученной в разряде постоянного тока, среднее межчастичное расстояние в горизонтальном сечении составило 0,4 мм, а среднее расстояние между четко различаемыми слоями в структуре – 0,2 мм. С учетом этой анизотропии эталонная автокорреляционная функция для модельной структуры с гранецентрированным типом упаковки выглядит следующим образом (рис. 5).

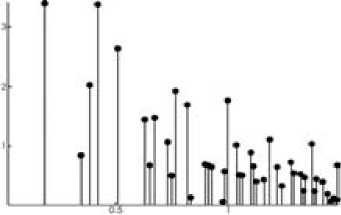
Рис. 5. Парная корреляционная функция для модельной гранецентрированной решетки, модифицированной с учетом анизотропии изучаемой структуры

Положения первых максимумов показанной на рисунке функции совпали с первыми максимумами функции g(r), полученной из эксперимента. Однако наличие большого числа побочных максимумов затрудняет адекватное сравнение исходной функции с эталонной. В качестве решения этой проблемы предлагается создать разброс в положениях частиц модельной структуры. Максимумы эталонной функции становятся существенно более плавными, и их число уменьшается за счет слияния с соседними (рис. 6).

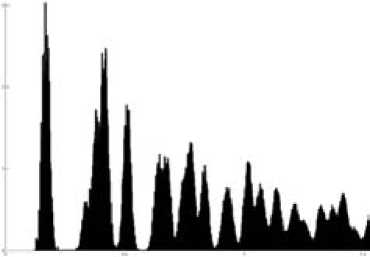
Рис. 6. Парная корреляционная функция для модельной структуры с добавлением разброса в положениях частиц

Величина разброса имеет нормальное распределение.

Этот метод позволяет классифицировать наблюдаемые на опыте трехмерные объекты как по степени упорядоченности, так и по типу упаковки в случае высокоупорядоченных структур (рис. 7).

Сравнение проводилось с гексагональной (a), с тетрагональной (модифицированной кубической) (b), с ромбической (модифицированной гранецентрированной fcc) (c) решетками. Наилучшее соответствие – на рис. 7c.

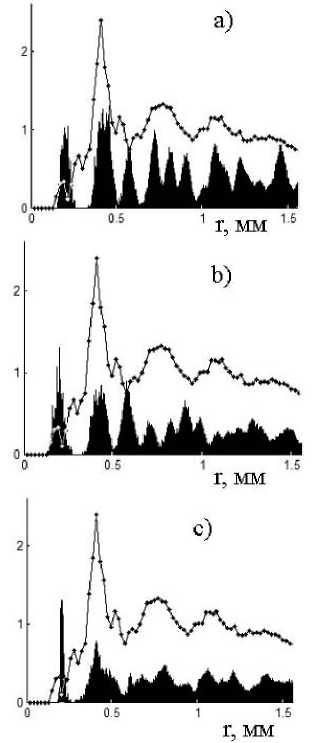
Рис. 7. Сравнение g(r) высокоупорядоченной структуры с анизотропными функциями g(r) модельных решеток, координаты которых возмущены случайной величиной, распределенной по нормальному закону со средним отклонением в 3 % от величины межчастичного расстояния