Методы исследования влияния технологических погрешностей на напряженно-деформируемое состояние многослойных композитных панелей

Создание современной авиационно-космической техники нового поколения с высокими тактико-техническими характеристиками является важной и достаточно острой научно-технической проблемой. К ряду таких проблем относится и создание конструкций зеркальных антенн, меняющих свое состояние при переводе из транспортируемого положения в рабочее и вызванная необходимостью в связи с запуском ИСЗ и созданием подвижных станций спутниковой связи. Ее успешное решение состоит в том, чтобы приблизиться к теоретическому профилю поверхности с заданной степенью точности для исключения фазовых ошибок в антенне. Основными причинами фазовых ошибок являются неточное изготовление поверхности отдельных элементов зеркала, отражающая поверхность конструкции антенны, выполненная из последовательности отдельных элементов, неточная установка их центра относительно фокуса зеркала [1].

го натяжения армирующих волокон, несиммет-рии свойств структуры пакета КМ по толщине и др. В реальных конструкциях из КМ “случайная” анизотропия материала, связанная с технологическими погрешностями и дефектами чередующих слоев, проявляется в условиях эксплуатации как отклонение от расчетной теоретической формы [1, 4]. Поэтому, одним из актуальных вопросов проектирования наиболее распространенных элементов авиационно-космических конструкций – многослойных прямоугольных панелей– является обоснование и внедрение в практику расчетов новых расчетных схем, которые отражая специфику работы тонкостенных пространственных систем, были бы в тоже время эффективными с точки зрения построения решения. При этом теоретический анализ напряженно – деформированного состояния позволяет создавать эталон деформирования рабочей поверхности антенны в условиях нагружения механическими и тепловыми нагрузками.

Рассмотрим определение напряженно – деформированного состояния (НДС) многослойной прямоугольной панели, выполненной из слоистых композиционных материалов. Многослойный несущий пакет плоских панелей тонкостенных пространственных конструкций обладает анизотропией вследствие несимметрии свойств структуры по толщине и в плане, вызванной погрешностями технологического процесса (углы разориентации в монослое, изменение объемного содержания волокна и матрицы в монослоях и т.д.). Панель изготовлена при температуре отверждения Т , охлаждена до комнатной температуры и находится под действием поперечной погонной нагрузки q(x,y) и температурного поля Д Т [2, 3]. В целях повышения несущей способности конструкции армирующие

q(x,y), AT, КнВ<0

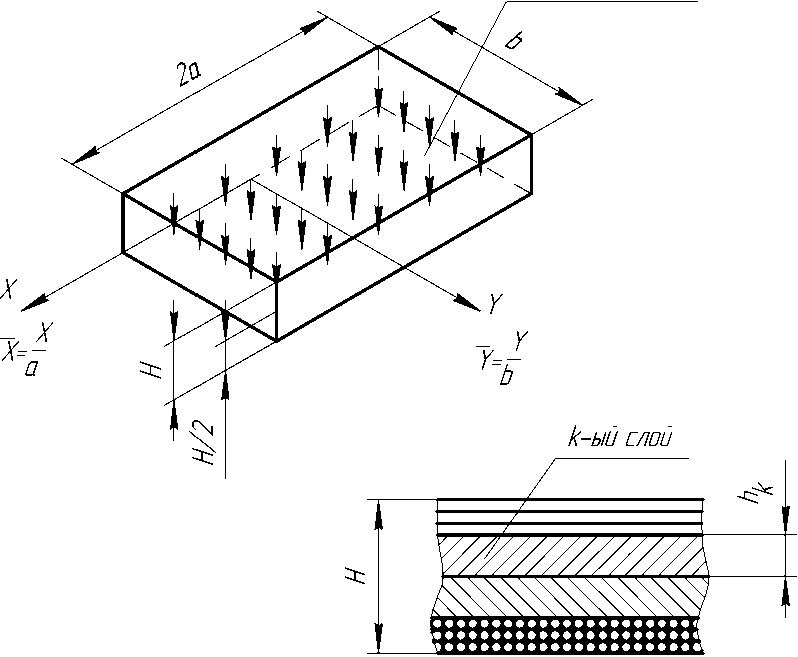
Рис. 1. Геометрическая модель и схема нагружения слоистой панели из композиционных материалов с несимметричной структурой по толщине, после отверждения под действием произвольной поперечной нагрузки q(x,y) и постоянного температурного поля A T = const

волокна предварительно натянуты, после отверждения натяжение снято (рис. 1).

Так как структура слоистого элемента несимметрична, то при последующей реализации гипотез о нормальном элементе в расчетной схеме теряется смысл срединной поверхности. Поэтому плоскость приведения, в которой рассматриваются координатные оси, и начало отсчета координаты в дальнейшем могут быть выбраны произвольно.

Задача решается в перемещениях с применением гипотезы Кирхгофа.

Математическая модель композитной многослойной панели может быть сформулирована путем введения в рассмотрение внутренних сил и моментов, действующих по площадкам поперечных сечений, и соответствующих им уравнений равновесия. Воспользовавшись соотношениями Коши, формулами геометрических преобразований, а также законом Гука с учетом влияния температуры, натяжения волокон и формулы преобразования напряжений при повороте осей выражения для компонентов напряженного состояния “ k ”-го слоя можно записать

{aJ }(К)(J = 1,2,6) — коэффициенты темпера турного расширения, {£hj }(K) J = 1,2,6 — дефор— мации натяжения слоя определяются через же-сткостные и температурные характеристики слоя, заданные в системе координат (рис.1) с ним связанной, с учетом поворота последней относительно декартовой системы координат панели (x,y) [5].

Погонные нормальные и сдвигающие силы, а также изгибающие и крутящие моменты для всего пакета, действующие, например, по площадке, перпендикулярной оси x , определяются интегрированием компонентов напряженного состояния по толщине, что обусловлено здесь возможностью распространения гипотезы Кирхгофа на все тело анизотропной среды:

H /2                    H /2

Nx = J ^xK) dz;   Nxy = JrxK) dz;

- H /2                   - H /2

в виде:

^ x

( K )

^a y

^T xy

где

Q Q Q

Q q

Q ₂6

Q^^{K )}

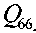
г +W z ⁽ K -cAK XT-AK

^U 0 x ^{+ w}»z    ^{a A} HH^

V oy - W /⁽ K -AT-^K    >(1)

U y + V x w ^{( K )} a AT -_e$ J

H /2                   H /2            ⁽²⁾

M x = J ^ xK ) zdz ;, H xy = J t X K ) zdz .

- H /2                  - H /2

Qj, ](K ’(I, J = 1,2,6)

– жесткости слоя,

Отсюда вытекают соотношения, связывающие внутренние силовые факторы с деформацией пакета:

N I

N I

д    Rif с 0 1   Г мТ 1   Г mb 1

AIJ   BIJ 1^/1   I N II

J —    1   —

D      pv ) ъг0 |    ) i tT Г   1 * д H |              ’

. bij d ij JI K j I    [ M i J    [ M i J I , J =1,2,6 ^v

⁽ x ^, y , xy '

где ⁽ A IJ , B IJ , D IJ ) - обобщенные жесткости многослойной панели (4).

H /2 — ( K )          N — ( K )

A u = J Q u dz = E Q u f ^{( K} ' ;

• — H /2

H /2 — ( K )           N — ( K )

B u = J Q u zdz = E Q u S ^{( K} ' ;

• — H/2

H /2 — ( K )             N — ( K )

Du = J Qu z ² dz = E Q ij J ^{( K} ' ;

• — H /2

Система дифференциальных уравнений с помощью операторного метода может быть сведена к одному разрешающему дифференциальному уравнению относительно некоторой потенциальной функции Ф(x,y), через которую выражаются все расчетные величины задачи. Согласно этому методу общий интеграл системы ищется таким образом, чтобы тождественно удовлетворялись первые два ее однородные соотношения. При этом перемещения определяются – в терминах символического интегрирования – минорами детерминанта det [ L_IJ ] , I,J =1,2,3, составленными по его третьей строке, соответствующей неоднородному уравнению системы (7).

В результате имеем:

^U 0 = ^L 12 ^L 23

^L 22 ^L 131 ^ ;

^V 0 =  | ^L 11 ^L 23    ^L 21 L 13 \Ф ;

N T , N T , N Ty , M x , M Y , H Ty - “температурные” усилия и моменты:

{ N T } = A T E [ Q ij ] ⁽ K V } ⁽ K ) F ^{( K} ) ;

k =1

{ M T } = A T E [ Q ij ] ⁽ K ) 0, } ^{( K} ) S ^{( K} ) I , J =1,2,6 , (5) k ^{1                                      (} x , y , xy )

HHH H HH a Nx , Nv , Nxv, Mx , Mv , Hxv - усилия и моменты x y xy x     y xy от натяжения:

^W = | L 11 ^L 22 ^L 21 ^L 12 | ^Ф .

В развернутом виде для U_{0 ,} V_{0 ,} W коэффициенты R _IJ, стоящие перед производными, зависят от обобщенных жесткостей многослойной панели ( A_IJ , B_IJ , D_IJ ) , например:

(R₅₀ 5 ⁵     R₄₁ 5 ⁵       R₃₂     5 ⁵

U = -2⁰1 ⁴¹ 1 ³² +

( a ⁵ 5 x⁵   a⁴ b 5 x ⁴ 5 y a³ b ² 5 x ² 5 y³

N

{ n H } = E [ Q ,j ] ^{( K} ^J } ^{( K )} F ^{( K )} ;

k =1

++ R^ RL ) ab ⁴ 5 x 5 y⁴   b⁵ 5 y ⁵ J

Ф .

N

{MIH }= E [Qij ](K ){^IJ}(K) S(K K k=1

I , J = 1,2,6 •

⁽ x , y , xy )

В свою очередь, f ^{( K} ' , S ^{( K} ' , J ^{( K} ' — погонные площадь, статический момент и момент инерции “ k ”-го слоя соответственно.

Так как усилия и моменты зависят как от деформации в плоскости панели, так и от кривизны поверхности приведения, в рассматриваемом случае из-за несимметрии свойств структуры пакета по толщине задача не разделяется на плоскую и изгиб пластины. Уравнения равновесия многослойной панели при действии внешней поверхностной нагрузки в направлении нормали к панели, записанные через обобщенные силовые факторы могут быть сведены путем исключения перерезывающих сил к системе трех дифференциальных уравнений относительно трех искомых функций U0 (x,y), V0(x,y), W(x,y), которая в операторном виде принимает вид:

L 11 U о + L 12 V 0 + L 13 W = 0 ;

L 21 U 0 + L 22 V 0 + L 23 W = 0 ; (7) l 31 U 0 + l 32 v 0 + l 33 W = — q ,

для W и V ₀ – аналогично.

Если структура композиционного материала ортотропна, а именно A₁₃ = A₂₃ = 0 и, кроме того, жесткостями B₁₃, B₂₃, D₁₃, D₂₃ можно пренебречь по сравнению с остальными характеристиками, в уравнении пропадут коэффициенты, стоящие при нечетных производных обобщенной функции перемещений Ф(x,y) по x и по y , т.е. К₇₁ = К₅₃ = К₃₅ = К₁₇ = 0.

Разрешающим уравнением задачи будет неоднородное линейное дифференциальное уравнение восьмого порядка в частных производных относительно обобщенной функции перемещений Ф(x,y) [6]:

K 80 5 ⁸ Ф + K 62 5 ⁸ Ф + K 44 5 ⁸ Ф + a⁸ 5 x⁸ a⁶ в ² 5 x ⁶ 5 y ² a⁴ в ⁴ 5 x ⁴ 5 y⁴

K₂₆   5 ⁸ Ф   K_№ 5 ⁸ Ф

26                    08

⁺ 2 6 д 2д 6 ⁺    8 д 8 = q •       (10)

a в dx dy    в оy где X, Y – безразмерные координаты, отнесенные, соответственно, к длине панели “a” и ши-

рине панели “ b ”: X= , Y=

a

y _.

Коэффициенты

K _IJ (I,J = 0…8) выражаются через обобщенные жесткости многослойного пакета.

Рассмотрим определение основного напряженно-деформированного состояния многослойной панели из ортотропного композиционного материала, шарнирно-опертой по продольным и произвольным образом закрепленной по поперечным кромкам (рис. 1). Соответствующие граничные условия при y = 0 и y = 1 имеют вид: Wx ,(0,1)]= M y [ x ,(0,1)]= u ₀[ x ,(0,1)]= N y [ x ,(0,1)], (11)

Решение уравнения, удовлетворяющее краевым условиям, представим в одинарных тригонометрических рядах:

w

Ф ^{( x} , y ) = S Ф П ^{( x )sin(} nny ) , (12) n =1

где Ф_п ( x ) подлежит определению.

При построении обобщенной функции перемещений Ф(x,y) в виде разложения ее в ряды по системе тригонометрических функций, предполагается, что на границе перпендикулярной оси y , панель нагружена потоками касательных сил Nxy .

Исследуя далее задачу общего вида, в смысле граничных условий по поперечным кромкам, в решении для Ф_п ( x , y ) оставим четные и нечетные функции с точностью до четырех произвольных постоянных Ф(x,y) запишем в следующей форме:

w

Ф(x, У) = S SAnLshUl) + SBnLchUl) + Ф и sin( nny)

При изгибе панели постоянной поперечной нагрузкой q ( x , y ) = const :

1  4 q

^ФП Ч^И = _r

K 08 ^{П П}

.

Компоненты вектора перемещений после соответствующих преобразований вычисляются по формулам:

w Г 4

w(x,У)= S SAWLsh(AL ■ x) + SBn ch'A " x)+ Wn n=1,3,5... L L=1

L = 1

U 0^{( x} , У )

' I ^x , у )

w 44

S S A L sh ( c  ■ x ) + S B U ch ( c . ■ x ) + ¹

n=1,3,5 LL=1

S SB'lch(al ■ x) + SB'Lsh(al ■ x) + In И n=1,3,5 L L=1

sin( n n y )

sin( n n y )

^J (15)

cos( n n y )

Аналогичным образом определяются и компоненты деформаций поверхности приведения, кривизны поверхности приведения и внутренние силовые факторы, действующие по площадкам, перпендикулярным осям x и y. Константы Д U0 RU0 4V0 RV0 Д W W Т/Г ттЛЛРТ/ГР TtVOTTQTTTT/TP AnL , BnL , AnL , BnL , AnL , BnL и другие, входящие в компоненты кривизн, деформаций и внутренних силовых факторов, как и все частные интегралы, например, Wnч/и , '0„ч/И , U0„ч/И выра- жаются через AnL,BnL и Ф„ч/И .

Раскладывая в тригонометрические ряды внутренние силовые факторы, например, по площадке, перпендикулярной оси x , связанные с температурой и натяжением, имеем:

w

N T ⁽ Н ) = S N Xnч/и •^sin( nn );

n =1,3,5

_N Т ( Н )    _ ^{4 N} x .

N xn   Ч!И          ;

1 nn

w

N TН ) = S N x y n ₄ m •^{cos( n n} y );

n =1,3,5

N xTn^H ) ч/и = 0;              (16)

w

M T ⁽ Н ) = S ^{м Т} пчи •^sin( nn );

n =1,3,5

_M I ⁽ Н )    ₌ ⁴ Mx .

xn Ч И            ;

' nn

Для окончательного определения компонентов напряженно-деформированного состояния, т.е. по существу, системе неизвестных констант A _nL и B _nL , необходимо удовлетворить граничным условиям на торцах конструкции при x = ±1 .

В общем случае упругая заделка позволяет рассмотреть все варианты краевых условий в отношении плоской задачи и задачи изгиба: защемлённый край, скользящую заделку, шарнир и свободные кромки.

При симметричной заделке по торцам, то есть, при x = ±1 :

( Y 1 U 0 + 5 1 N x ) = ( y ₂ V 0 + J 2 N xy ) =

= ( Y 3 W + 5 3 Q x ) = ( Y 4 0 x + 5 4 M x ) = 0 . (17)

При несимметричной заделке по торцам при x = +1 :

( Y 1 U 0 + 5 1 N x ) = ( Y 2 V 0 + 5 2 N xy ) =

= ( Y 3 W + 5 3 Q x ) = ( Y 4 0 x + 5 4 M x ) = 0 , (18) а при x = - 1 :

( ^ 1 U 0 + Z 1 N x ) = ( ^ 2 V 0 + z 2 N xy ) =

= ( Z 3 W + Z 3 Q x ) = ( ^ 4 0 x + Z 4 M x ) = 0 , (19)

После определения компонентов деформированного состояния и внутренних силовых факторов напряжения вычисляются по формуле:

( K )

^L x

L y

^T xy

Q u

Q 12 . Q 16

^Q 12

Q 22

Q 26

Q 16 T K )

Q 26

Q ..

£°_x + K x z-a ^K ) A T- (

^- 0 + K y z-« 2 ^K ) AT--<

Y xy + K z-а б ^K ) AT—>

В системе координат, связанной с направлением армирования “ k ”-го слоя, напряженное состояние определяется посредством преобразова-

ния при повороте осей:

L

( к )

L f

L 3

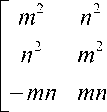
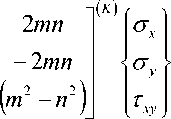
. (21)

Для оценки прочности многослойной панели из композиционного материала определяются относительные эквивалентные напряжения, для расчета которых использовался критерий прочности в форме Гольденблата-Копнова. Согласно критерию прочности Гольденблата-Копнова для однонаправленного слоя КМ, растрескивание или разрушение пакета не произойдёт, пока в каждом слое выполняется неравенство [6]:

1 f^₊^ 1 (.( K ) УД ( ' 1 ( K K ))2 ₊ K)

4 I ( ^K )     < 7 ) ^K ) I ^{( 1} ) 4I d-^{( K} )     < 7 ) ^K ) I ^{( 2} )      r⁽ K )

T..

\ 1 p       1 c /                 \ 2 p       2 c J                  12 7

+

11 1

1 Y

+— I--1--

2 ( L K )   L cK ),

_{L 1}( K )

11 1

1 Y