Методы измерения неравенства денежных доходов населения
Автор: Колмаков Игорь Борисович
Журнал: Народонаселение @narodonaselenie
Рубрика: Методы метстатистика в анализе благосостояния
Статья в выпуске: 2 (76), 2017 года.
Бесплатный доступ
В статье предлагается расширить состав показателей, характеризующих неравенство населения по уровню денежных душевых доходов (СДД). Индекс Джини не содержит количественной оценки доходов разных групп населения. Коэффициент фондов не отражает полную картину сложившегося неравенства. Поэтому автором предлагаются дополнительные экономически обоснованные показатели неравенства денежных доходов, которые получили название индексов поляризации. Используя различные характеристики логнормального распределения населения по денежному душевому доходу - среднедушевой доход, мода и медиана - в качестве границ, которые делят все население на две группы с доходом выше и ниже принятой границы вычисляются и сравниваются между собой показатели среднедушевого денежного дохода в этих группах населения. Установлено, что значения индексов поляризации зависят только от значений нормированных функций Лапласа, аргументами которых являются различные доли среднеквадратического отклонения логарифма доходов.
Неравенство, душевые денежные доходы, логарифмически нормальное распределение, параметры распределения, индексы поляризации
Короткий адрес: https://sciup.org/14347684
IDR: 14347684
Текст научной статьи Методы измерения неравенства денежных доходов населения
(исследование проведено при финансовой поддержке РГНФ, проект №16 — 02 – 00533/16)
Распределение населения по уровню среднедушевых денежных доходов (СДД), рассчитывается Росстатом с использованием логарифмически-нормального рас пределения [1; 2]. Кривая плотности вероятностей логарифмически нормального распределения населения по уровню СДД с параметрами µ и σ2(математическое ожидание и дисперсия логарифма дохода х) имеет вид:
(lnx- µ )2 - 2
f(x) = 1 e 2 σ (1)
σ⋅ x ⋅ 2π
Важнейшими индикативными характеристиками плотности логнормального распределения численности населения по уровню СДД являются [3; 4]: модальное значение X mod = exp( µ – σ 2); (2)
медианное значение X med = exp(µ); (3) среднее значение X c =exp( µ +0.5 σ 2). (4)
Между индикативными характеристиками существует параметрическая связь, определяемая дисперсией логарифма дохода -σ2. Чем больше значение σ2 или чем дальше находятся индикативные характеристики друг от друга, тем больше степень неравномерности доходов и выше степень расслоения населения.
Уравнения (2), (3) и (4) образуют три системы из двух уравнений с двумя неизвестными µ и σ . Решая любую из них, получаем параметры распределения µ и σ , выраженные через индикативные характеристики распределения ( X mod , X med и X c ), имеющие явный экономический смысл [3] . Так как все три системы уравнений описывают одно и тоже распределение населения по уровню СДД, то для всех трех систем уравнений параметры µ и σ должны быть одинаковы. Проверка этого утверждения на данных Росстата за 2015 год ( Х с = 30473,6 руб.; X med =22718,4руб.; X mod =12626,6 руб.) показала, что точность расчетов параметров распределения достаточно высокая [3]:
µ . = 10,0309307 ±0,0000003; σ = 0,7664008±0,0000005.
Для оценки неравенства, наряду с распределением численности населения, необходимо рассматривать распределение доходов населения.
Плотность вероятности распределе- ния доходов населения по уровню СДД — ϕ(x) — имеет вид:
(lnx- µ )2
-
ϕ (x) = 1 х ⋅ f(x) = 1 e 2 σ (5)
X c X c σ 2 π
Также как и для f(x) — плотности логнормального распределения численности населения по уровню СДД, для ϕ (x) — плотности логнормального распределения доходов населения, важнейшими индикативными характеристиками являются [3]: модальное значение плотности дохода X φmod = exp( µ ); (6)
медианное значение плотности дохода X φmed = exp(µ+ σ 2); (7)
среднее значение плотности дохода X φc = exp( µ +1,5 σ 2). (8)
Видно, что модальное значение плотности дохода ϕ (x) (6) в точности соответствует медианному значению плотности распределения численности населения f(x) (3).
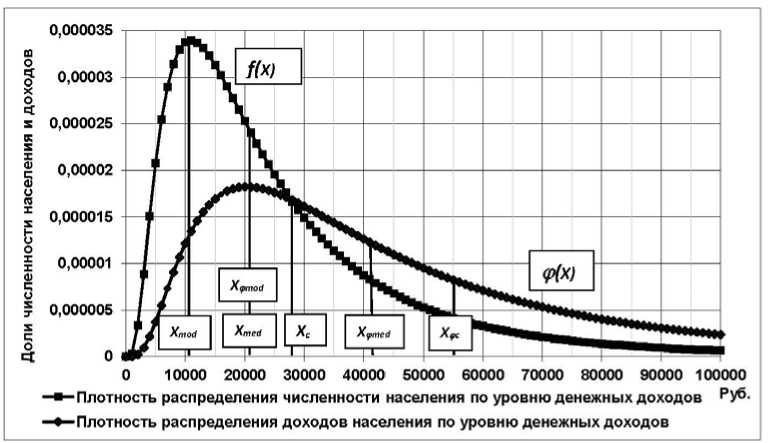
На рис. 1 приведены кривые ло-гарифмически-нормального распределения населения по уровню СДД — плотность вероятности распределения численности населения f(x) и кривая логарифмически-нормально-го распределения доходов по уровню СДД — плотность вероятности распределения доходов φ(x). На этих же кривых обозначены основные индикативные точки.
0,000035
0,00003
0,000025
0,00002
0,000015
0,00001
X^mod
0,000005
Xmod
Xymed
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
—•—Плотность распределения численности населения по уровню денежных доходов ^У®-
—♦—Плотность распределения доходов населения по уровню денежных доходов
Рис. 1. Графики плотностей распределения численности населения — f(x), денежного дохода — ф(х) и индикативные точки этих кривых
Интегральной характеристикой плотности вероятностей логарифмически нормального распределения населения по уровню среднедушевых денежных доходов является функция распределения накопленных долей численности населения:
x F(x) = ∫
1 σ 2 π
f(u)du =
x
1 e
0u
(lnu- µ )2 2 σ 2
du.
Накопленные доли доходов населения по уровню СДД есть интеграл или функция D(x) :
x
D(x) = ∫
ϕ (u)du =
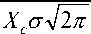
x - (lnu- µ )2
∫ e 2 σ 2 du.
Именно функции F(x) и D(x) определяют кривую Лоренца и индекс Джини, а следовательно, и дифференциацию денежных доходов населения. Эти функции позволяют определять, какая доля численности населения обладает каким объемом доходов. В работе [5] исследовалось поведение разности долей функций R(x) = F(x) — D(x) и установлены зависимости, определяющие связь индекса Джини с показателем распределения ст и нормированным значением интеграла R(x). На рис. 2 приведен вид интегральных характеристик функций F(x), D(x) и R(x).
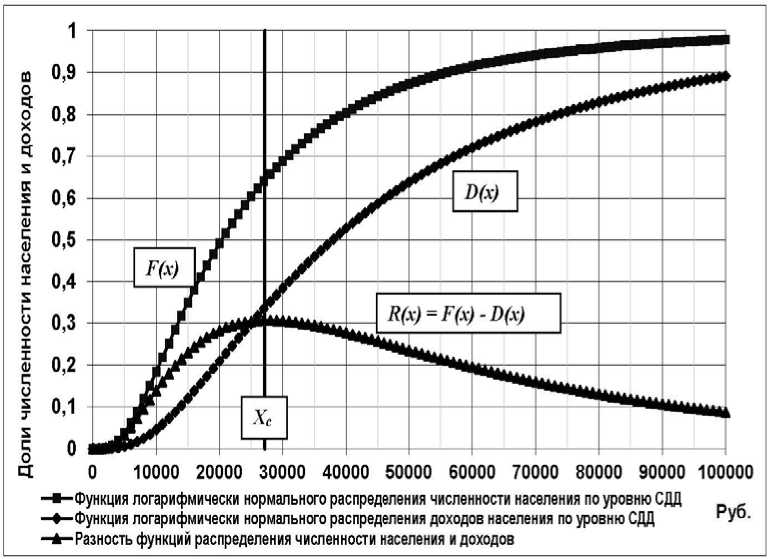
Рис. 2. Графики функций распределения по уровню СДД: накопленных долей численности населения — F(x), накопленных долей денежных доходов населения — D(x) и долей разности этих функций — R(x)
Индикативные полярные характеристики доходов населения
Социальная устойчивость общества определяется численностью и доходами «среднего класса». Из двух официально используемых показателей дифференциации доходов никак не следует оценка численности «среднего класса», кроме очевидного утверждения: «чем меньше индекс Джини, тем выше численность «среднего класса».
В процессе обсуждений проблем социальной устойчивости общества настоятельно выявлялась необходимость иметь такие характеристики доходов, которые позволяли бы оценивать расслоение населения по уровню денежных доходов относительно неких индикативных показателей доходов. Если условно X i считать индикативным доходом, то логично рассматривать характеристики (долю численности, долю дохода и средний доход) тех, кто имеет доходы ниже X i и тех, кто имеет доходы выше, и сравнивать их между собой.
Поскольку эти характеристики полярно отличаются по знаку оцениваемых параметров, то назовем эти характеристики расслоения населения по уровню денежных доходов полярными . При расчете полярных характеристик требования к ним были весьма простые: не противоречить общепринятым, не заменять, а дополнять существующие, отличаться простотой и ясностью экономической трактовки, и прозрачностью вычислений.
В качестве индикативных границ деления населения и, соответственно доходов, выберем индикативные показатели, имеющие явный экономический смысл: модальный доход (2), доход медианной численности населения (3), средний доход (4), медианное значение плотности дохода (7), среднее значение плотности дохода (8).
Фиксация границы расслоения на уровне выбранного индикативного дохода выявляет поляризацию населения и позволяет определить, какая часть населения имеет доходы ниже выбранного индикативного уровня, какой частью доходов владеет и какой средний доход в этой исследуемой группе. Точно также определяются характеристики группы населения, имеющего доходы выше выбранного уровня.
Сравнение средних доходов этих полярных групп населения позволяет получать количественную характеристику неравенства и не менее емко характеризуют дифференциацию доходов, чем индекс Джини. Поэтому предлагается наряду с уже используемыми показателями дифференциации рассматривать другие показатели: индексы поляризации денежных доходов населения:
-
1) индекс поляризации модального дохода ( X mod) IMD ;
-
2) индекс поляризации дохода медианной численности ( X med) IME ;
-
3) индекс поляризации среднего доход а( X c ) ISR ;
-
4) индекс поляризации численности медианного дохода ( X ^ med ) IMR ;
-
5) индекс поляризации среднего значения плотности дохода ( X ϕ c ) ISD .
Методы расчета всех индексов поляризации одинаковы1. Поэтому далее приводится только расчет индекса поляризации модального дохода — IMD. Для других индексов пред- ставлены конечные результаты — формулы и графики, которые позволяют понимать трактовку и получать их количественные оценки.
Индекс поляризации модального дохода — IMD
Если индикативной границей доходов населения считать модальный доход X mod , то индекс поляризации модального дохода предлагается определять, как отношение среднего дохода в относительно высокодоходной группе населения (ВДГ) к среднему доходу в относительно низкодоходной группе (НДГ).
Доля численности тех, кто имеет доходы ниже модального значения, равна:
F Lmod (X mod ) = Ф(- σ ) = 1 – Ф( σ )
Доля доходов низкодоходной группы в общем объеме доходов населения составит:
D Lmod (X mod ) = Ф(-2 σ ) = 1 – Ф(2 σ )
Тогда средний доход в группе населения с доходами ниже модального уровня равен:
SD Lmod = Ф(-2 σ )/Ф(- σ ) = (1 – Ф(2 σ ))/ (1 – Ф( σ ))
Аналогичные расчеты проводятся для группы населения с доходами выше модального уровня. Последовательно вычисляется доля численности этой группы населения, доля доходов этой группы в общем объеме доходов и средний доход:
F Hmod (X mod ) = 1 – Ф(- σ ) = Ф( σ );
D Hmod (X mod ) = 1 – Ф(-2 σ ) = Ф(2 σ );
SD Hmod = Ф(2 σ )/Ф( σ ).
Отношение средних доходов населения в группе с доходами выше модального уровня, к средним доходам населения в группе с доходами ниже модального уровня дает очень простую и наглядную процедуру построения индекса поляризации модального дохода (рис. 3).
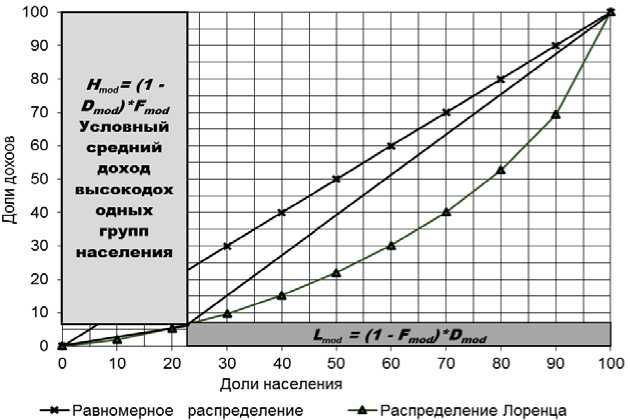
Рис. 3. Графическая интерпретация индекса поляризации модального дохода IMD
Через точку с координатами модального дохода (F Lmod (X mod ); F Lmod (X mod )) проводятся горизонталь и вертикаль до пересечения с осями координат. В левом верхнем углу и правом нижнем образуются два прямоугольника. Площадь левого верхнего прямоугольника
H mod = (1 — D Lmod (X mod )) • F l mod (X mod ), трактуется как условный средний доход населения с доходами выше модального, а площадь прямоугольника в правом нижнем углу
L mod = (l-F Lmod (X mod )) • D Lmod (X mod ) — как условный средний доход населения с доходами ниже модального. Отношение площадей прямоугольников H mod и L mod и есть индекс поляризации модального дохода:
IMD = H mod /L mod = ( 1 — D Lmod (X mod )) *
F l mod (X mod )/ ((1 – F Lmod (X mod )) •
D Lmod (X mod )) = (Ф(2 о )/Ф( о )) . (1 -
Ф( σ ))/(1 – Ф(2 σ )) (11)
В случае «абсолютного равенства» H mod = L mod индекс поляризации IMD = 1 . В случае «абсолютного неравенства» H mod → 1 и L mod → 0 и индекс поляризации IMD →∞ .
Теоретический диапазон изменения индекса поляризации модального дохода 1 < IMD < ∞ , а фактический — значительно меньше.
Индекс поляризации дохода медианной численности IME
Индикативной границей доходов в этом случае принимается доход, соответствующий доходу медианной численности населения X med . Доля численности тех, кто имеет доходы ниже медианного уровня и доля численности тех, кто имеет доходы выше медианного, равны Ф(0) = 0,5.
F Lmed (X med ) = Ф Lmed (v med ) = 0,5.
Доля дохода D Lmed (X med ) и средний доход SD Lmed в группе населения с доходами ниже медианного дохода составляют:
D Lmed (X med ) = Ф(- σ ) = 1 – Ф( σ );
SD Lmed = Ф(- σ )/0,5 = (1 – Ф( σ ))/0,5.
Аналогичные показатели для группы с доходами выше медианной численности:
D Hmed (X med ) = 1 – Ф(- σ ) = Ф( σ );
SD Hmed = Ф( σ )/0,5 = (1 – Ф(- σ ))/0,5.
Индекс поляризации дохода медианной численности:
IME = SD Hmed /SD Lmed = Ф( σ )/Ф(- σ ) = Ф( σ )/(1-Ф( σ ))
Графическая интерпретация индекса поляризации дохода медианной численности приведена на рис. 4. Через точку на кривой Лоренца с координатами { 0,5 ; D Lmed (X med ) } проводятся горизонталь и вертикаль до пересечения с осями координат. В левом верхнем углу и правом нижнем образуются два прямоугольника.
Площадь левого верхнего прямоуГОЛЬНИКа H med = (1 — D Lmed (X med )) • 0,5 трактуется как условный средний доход населения с доходами выше дохода медианной численности , а площадь прямоугольника в правом нижнем углу L med = 0,5 • D l med (X med ) — как условный средний доход населения с доходами ниже дохода медианной численности.
Отношение площадей прямоугольников H med и L med и есть индекс поляризации дохода медианной численности:
IME= H med /L med = ( 1 — D Lmed (X med )) • 0,5/0,5 • D Lmed (X med ) = Ф( о )/(1 — Ф( о )) (12)
В случае «абсолютного равенства» H med = L med и индекс поляризации IME= 1 .
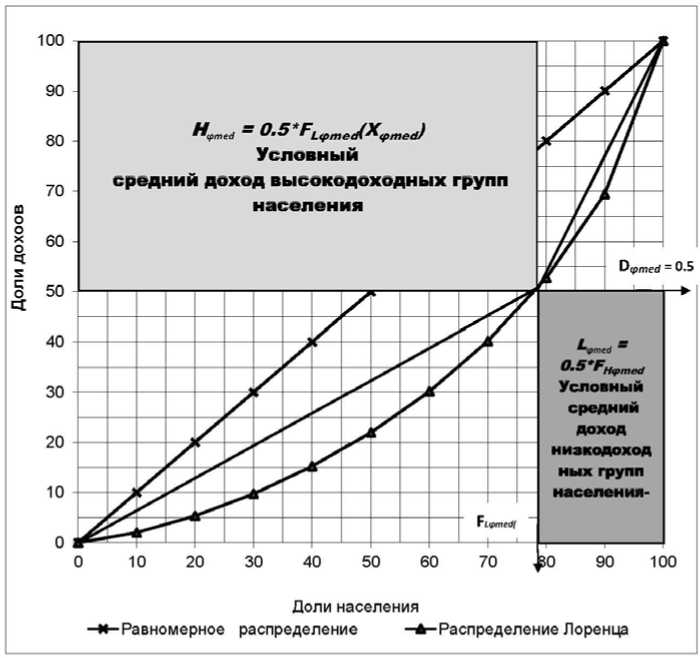
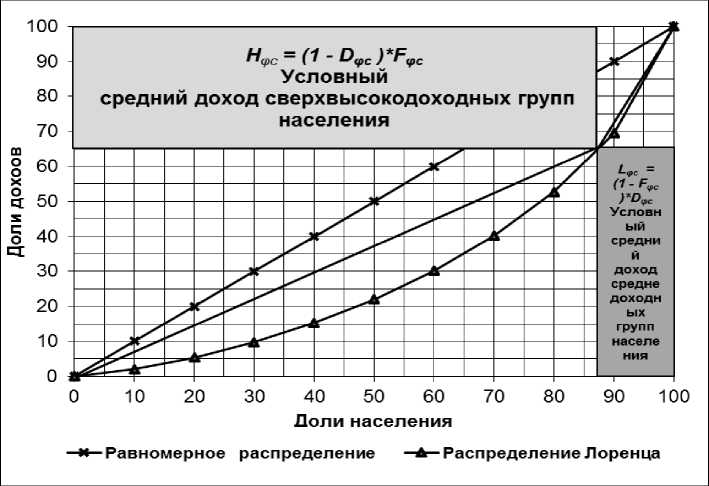
В случае «абсолютного неравенства» Hmed→ 1 и Lmed→ 0 и индекс по- ляризации IME→∞. Теоретический диапазон изменения индекса 1 Рис. 4. Графическая интерпретация индекса поляризации дохода медианной численности IME Индекс поляризации численности медианного дохода IMR Индикативной границей доходов в этом случае принимается доход, соответствующий численности медианного дохода населения Xφmed = exp(µ+σ2). По аналогии с расчетами исходных данных для индекса поляризации медианной численности дохода определяются исходные данные для расчета индекса поляризации медианного дохода — IMR: Flφmed(Xφmed) = ФLφmed(vφmed) = Ф(σ); DLφmed(Xφmed) = Ф(0) = 0,5; SDLφmed = 0,5/Ф(σ); FHφmed(Xφmed) = ФHφmed(vφmed) =1 – Ф(σ); Dнфmed(Xфmed) - Ф(0) = 0,5; SDHφmed =0,5/(1 – Ф(σ)). Индекс поляризации численности медианного дохода: IMR = SDнфmed/SDLфmed= Ф(о)/(1 — ФИ) Графическая интерпретация индекса поляризации численности медианного дохода приведена на рис. 5. Рис. 5. Графическая интерпретация индекса поляризации численности медианного дохода IMR Через точку на кривой Лоренца с координатами {FHφmed(Xφmed); 0,5} проводятся горизонталь и вертикаль до пересечения с осями координат. Площадь левого верхнего прямоуГОЛЬниКа Hфmed = Fнфmed(Xфmed) • 0,5 трактуется как условный средний доход населения с доходами выше медианного дохода, а площадь прямоугольника в правом нижнем углу Lфmed = (1 — Fнфmed(Xфmed) • 0,5 — КаК условный средний доход населения с доходами ниже медианного дохода. Индекс поляризации численности медианного дохода есть отношение площадей прямоугольников Hφmed и Lφmed: IMR = Hφmed/Lφmed = Ф(σ)/(1 – Ф(σ)) (13) В случае «абсолютного равенства» Hφmed = Lφmedи индекс поляризации IMR = 1. В случае «абсолютного неравенства» Hφmed→ 1 и Lφmed→ 0 и индекс поляризации IMR→∞. Теоретический диапазон изменения индекса поляризации численности медианного дохода 1 <IMR<∞, а фактический рабочий диапазон изменения значительно меньше. Сравнивая формулы вычисления индекса поляризации дохода медианной численности IME (12) и индекса поляризации численности медианного дохода IMR (13) отмечаем, что они полностью совпадают. В практике международных сравнений неравенства используются именно эти оценки координат кривой Лоренца [8]. Для оценки дохода медианной численности: Flmed(Xmed) = Fhmed(Xmed) =Ф(0) =0,5 и DLmed(Xmed)= 1 – Ф(σ); для оценки численности медианного дохода: Dнфmed(Xфmed) — DLфmed(Xфmed) = Ф(0) = 0,5 и FLφmed(Xφmed) = Ф(σ). Индекс поляризации среднего значения плотности дохода ISD Индикативной границей доходов в этом случае принимается доход, определяемый формулой среднего значения плотности дохода: Xφc = exp(µ +1,5σ2) (8). Исходные данные для расчета индекса ISD: FLφc(Xφc) = ФLφc(vφc) = Ф(1,5σ); DLφc(Xφc) = Ф(0,5σ); SDLφc = Ф(0,5σ)/Ф(1,5σ); FHφc(Xφc) = 1 – Ф(1,5σ)/DHφc(Xφc) = 1 – Ф(0,5σ); SDHφc = (1 – Ф(0,5σ))/(1 – Ф(1,5σ)). Индекс поляризации среднего значения плотности дохода ISD: ISD = SDHφc/SDLφc= ((1 – Ф(0,5σ))/(1 –Ф(1,5σ)))/(Ф(0,5σ)/Ф(1,5σ)) Графическая интерпретация индекса поляризации среднего значения плотности дохода приведена на рис. 6. Через точку на кривой Лоренца с координатами {FLφc(Xφc); DLφc(Xφc)} проводятся горизонталь и вертикаль до пересечения с осями координат. В левом верхнем углу и правом нижнем образуются два прямоугольника. Площадь левого верхнего прямоугольника Нфс — FLфc(Xфc) • (1 -DLφc(Xφc)), а площадь прямоугольника в правом нижнем углу Lφc = (1 – FLфc(Xфc)) • DLфc(Xфc). Отношение площадей прямоугольников Hφc и Lφc и есть индекс поляризации среднего значения плотности дохода. ISD= Нфс/Ьфс= FLфc(Xфc) • (1 - DLфc(Xфc))/(1 — FLфc(Xфc)) • DLфc(Xфc) = = ((1 -Ф(0,5п)) • Ф(1,5а))/(Ф(0,5а) • (1 – Ф(1,5σ))) (14) В случае «абсолютного равенства» Hφc = Lφc и индекс поляризации ISD = 1. В случае «абсолютного неравенства» Hφc→ 1 и Lφc→ 0 и индекс поляризации ISD→∞. Теоретический диапазон изменения индекса поляризации среднего значения плотности дохода 1 <ISD<«, а фактический — значительно меньше. Рис. 6. Графическая интерпретация индекса поляризации среднего значения плотности дохода ISD Величины индексов поляризации — аналог коэффициента фондов, так как определяются отношением средних доходов в группах населения с доходами выше и ниже принятой границы доходов. В отличие от коэффициента фондов здесь граница, а соответственно, и численность населения в группах не остаются постоянной величиной, зависит от среднеквадратического отклонения логарифмов доходов. Оценка точности вычисления индексов поляризации зависит только от точности определения величины среднеквадратического отклонения, которая в свою очередь зависит от точности исходных данных. Индексы поляризации наряду с индексом Джини, рекомендуются для оценки неравенства населения по уровню денежных доходов. Выбор индексов зависит от поставленных целей анализа или прогноза.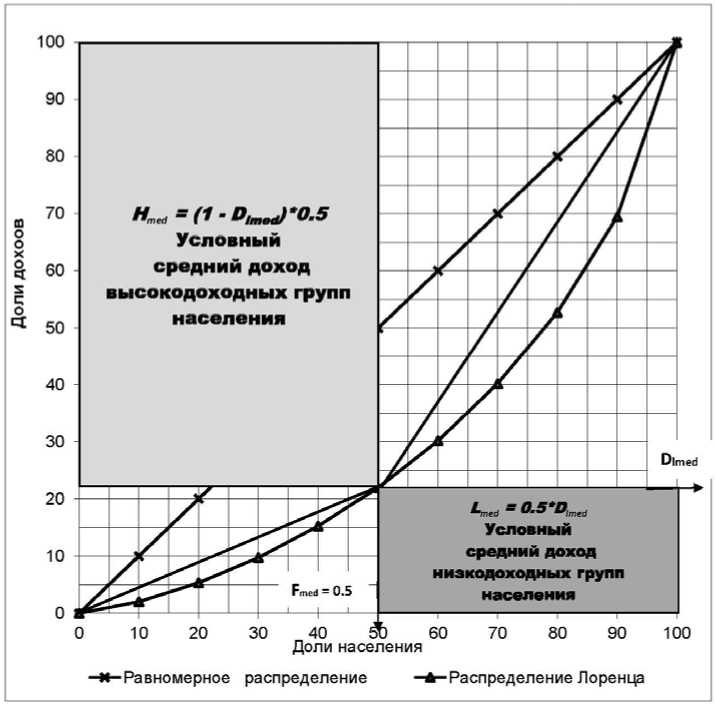
Список литературы Методы измерения неравенства денежных доходов населения
- Методологические положения по статистике. Вып. 1. -М.: Госкомстат России, 1996. -674 с.
- Великанова Т.Б., Колмаков И.Б., Фролова Е.Б. Совершенствование методики и моделей распределения населения по среднедушевому доходу//Вопросы статистики. -1996. -№ 5 -1996. -С. 50-58.
- Великанова Т.Б. Средний, медианный и модальный уровень денежных доходов населения в целом по России и по субъектам Российской Федерации. . -Режим доступа: http://www.gks.ru/free_doc/new_ site/population/bednost/tabl/tab-bed1-2-6.htm(дата обращения 29.04.2017)
- Социальное положение и уровень жизни населения России. Стат. сб. -М.: Росстат, 2000-2016.
- Колмаков И.Б. Методология измерения неравенства денежных доходов населения: анализ и прогноз показателей дифференциации и поляризации//Аудит и финансовый анализ. -2016. -№6. -С. 409-424.
- Колмаков И.Б. Методология анализа интегральных оценок показателей поляризации денежных доходов населения//Вопросы статистики. -2015. -№ 2. -С. 23-36.
- Колмаков И.Б. Методы и модели прогнозирования показателей дифференциации и поляризации денежных доходов населения: Дисс. … д-ра экон. наук. -М., 2008.
- Миланович Б. Глобальное неравенство доходов в цифрах: на протяжении истории и в настоящее время: Обзор: докл. к XV Апр. Межд. науч. конф. по проблемам развития экономики и общества, Москва, 1-4 апреля 2014 г./Пер. с англ. -М.: ИД ВШЭ, 2014.


