Методы квантового машинного обучения для обнаружения атак на программно-конфигурируемые сети

В последние годы распространение сетевых атак и нарушений безопасности стало растущей проблемой как для организаций, так и для отдельных лиц [1] . Для защиты сетей от них разработаны системы обнаружения вторжений (СОВ, IDS). Однако традиционные системы обнаружения вторжений часто не могут идти в ногу с растущей сложностью и изощренностью современных атак. Следовательно, существует острая необходимость в инновационных подходах, которые могут повысить точность и эффективность обнаружения вторжений. Машинное обучение (ML) является одним из таких подходов, который показал многообещающие результаты в повышении точности и эффективности IDS. Системы обнаружения вторжений на основе ML оказались важным масштабируемым инструментом для защиты сетей от кибератак, они способны к самообучению, а также могут работать при относительно небольших мощностях с достаточной скоростью, в отличие от классических IDS [2] .

Квантовые вычисления, являясь относительно молодой областью, предлагают значительное ускорение для многих задач за счет квантового параллелизма и других принципов квантовой физики, поэтому имеет смысл приложить их и к области ML. В данной работе рассматривается задача обнаружения вторжений в программно-конфигурируемых сетях с помощью методов квантового машинного обучения. В частности, рассматривается применение метода VQC, который пользуется большой популярностью у исследователей [3] .

Сети традиционной архитектуры широко и успешно используются, но для больших сетей (например, дата-центров) необходима более высокая скорость реагирования на изменения и более высокая степень автоматизации, которые с помощью традиционной архитектуры не могут быть реализованы, даже при наличии высококлассных специалистов. Программно-конфигурируемая сеть (ПКС, SDN) — это концепция сети, которая отделяет плоскость управления от плоскости передачи данных [4] . Основной особенностью данной архитектуры является централизованное управление всей сетью с одного контроллера, что повышает гибкость сети и ее способность расти. Контроллер SDN может выполнять функции, связанные с управлением сетью, такие как конфигурация коммутаторов, упорядоченная доставка пакетов, получение статистических данных коммутатора и другие [5] . Архитектуру SDN можно представить схематично, как показано на рисунке 1 [6] .

Приложение

Приложение

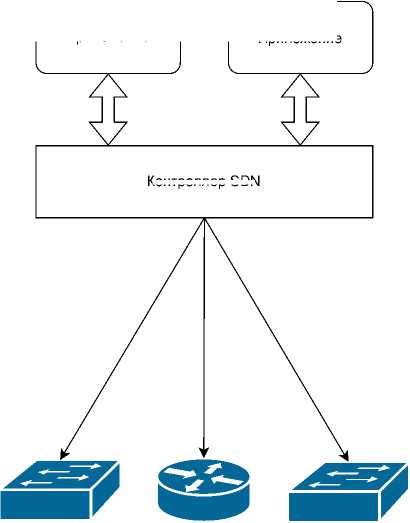
Контроллер SDN

Рисунок 1. Архитектура SDN

Уровень приложений

Уровень управления

Канал управления

Уровень данных

Разделение уровня управления сетью и уровня передачи данных в сети SDN приводит к следующим преимуществам [7] :

• ^•    Отделение плоскости управления от плоскости данных облегчает управление сетью. Кроме того, сеть становится легче изменять и обновлять, что снижает количество человеческих ошибок.

• ^•    ИТ-администраторы могут легко добавлять сетевые устройства или модернизировать сетевую инфраструктуру, не привязываясь к конкретному поставщику оборудования.

• ^•    Низкоуровневые инфраструктурные устройства не требуют отдельного программирования, что значительно снижает эксплуатационные расходы по сравнению с обычной сетью.

Обнаружение вторжений — это задача классификации, распределяющая входящий сетевой трафик на классы: обычный и вредоносный [8]. Сами атаки на программно-конфигурируемые сети можно классифицировать на 4 категории [9]: удаленные атаки на плоскость управления сетью, локальные атаки на плоскость управления сетью, атаки на канал управления сетью (особенно, протокол OpenFlow, используемый в SDN) и атаки на уровень передачи данных.

1.    Особенности квантовых вычислений

Квантовые вычисления — это относительно новая область, которая объединяет компьютерные науки, математику и физику. Эта область исследует возможности использования принципов квантовой физики для создания квантовых компьютеров, использующих квантовые биты (кубиты), которые могут содержать комбинации значений 0 и 1 в суперпозиции одновременно.

Так как кубиты могут находиться одновременно в нескольких состояниях, временные затраты на расчет каждого состояния не требуются, а общее время расчётов уменьшается. Именно такая возможность позволяет решать некоторые сложные задачи быстрее классических компьютеров [10 , 11] .

Классический компьютер с памятью из n бит может одномоментно выполнить некоторую операцию только над одним из 2n возможных наборов. Чтобы вычислить значение некоторой булевой функции от n аргументов для всех значений аргументов с помощью классического компьютера, придётся по очереди перебирать все 2n наборов и вычислять значение функции на каждом наборе по отдельности. Благодаря квантовой суперпозиции, в квантовом компьютере с n кубитами можно одновременно представить все 2n набора и выполнять операции над всеми наборами сразу. В результате возможно вычислить значение функции сразу для всех 2n комбинаций значений аргументов [12] .

Кубит можно определить, как вектор единичной длины в двумерном гильбертовом пространстве над полем комплексных чисел. Состояния 0 и 1 вместе представляют собой базисные вектора. Каждое из состояний кубита может быть представлено суперпозицией двух базисных состояний, которые обычно обозначаются как | 0 ) и | 1 ) . Формула, представляющая кубит в суперпозиции, выглядит следующим образом:

| ^ ) = а0 + в | 1 ) ,

α и β - комплексные числа, известные как амплитуды. Сумма их квадратов должна быть равна 1, поэтому можно сказать, что они определяют вероятности обнаружения кубита в каждом из базисных состояний.

Однако создание и манипулирование кубитами само по себе не является достаточным для выполнения сложных операций. Для реализации квантовых алгоритмов необходимо уметь манипулировать состояниями кубитов с высокой степенью контроля. Это достигается с помощью квантовых вентилей [10] . Квантовые вентили представляют собой аналоги классических логических вентилей, которые выполняют различные операции над кубитами, такие как логические, унитарные и нелинейные. Квантовые вентили используются для создания квантовых цепей и выполнения последовательности операций, составляющих квантовый алгоритм. Благодаря квантовым вентилям получается достичь эффективности и гибкости квантовых вычислений.

Квантовые вентили можно представить в виде унитарных матриц, которые преобразуют входной кубит в выходной кубит. Для любого входного состояния кубита, квантовый вентиль выполняет преобразования в соответствии с определенными правилами. Например, вентиль NOT инвертирует состояние кубита. Тем не менее, квантовые вычисления на данный момент используются только в исследовательских целях и не распространены для массового использования. Рассмотрим основные препятствующие этому проблемы:

• (1 )    Декогеренция представляет собой явление, при котором квантовая система взаимодействует с окружающей средой, что приводит к потере квантовых свойств и, следовательно, к ухудшению точности и стабильности вычислений [13] . Максимальное время жизни квантовой системы, когда она пригодна для квантовых вычислений, крайне мало, а по окончании этого времени система начнет выдавать белый шум вместо вероятностных распределений.

• (2)    Одним из наиболее актуальных вызовов является масштабируемость квантовых систем. В настоящее время существуют квантовые компьютеры с небольшим числом кубитов, однако для решения реальных задач требуется значительное увеличение их мощности [11] . Разработчикам необходимо искать пути увеличения числа кубитов и улучшения их производительности, чтобы обеспечить масштабируемость и применение квантовых систем для решения широкого спектра задач.

• (3 )    Другим важным вызовом является сложность реализации квантовых систем. В отличие от классических вычислительных систем, которые имеют долгую историю и разработанную методологию, квантовые системы находятся на стадии активных исследований и разработок. Например, нет четких методик устранения “багов”, специфичных для

квантовых компьютеров, из-за чего во время их работы возникают ошибки [14] .

Рассмотрим также основные приложения квантовых вычислений:

• (1)    Алгоритм Шора [15,16] представляет собой квантовый алгоритм, способный эффективно факторизировать большие целые числа. Факторизация является процессом разложения числа на простые множители. На классических компьютерах, работающих на классических алгоритмах, факторизация достаточно больших чисел требует экспоненциального времени, что делает ее практически невозможной для чисел с достаточной длиной для применения в криптографических системах. Алгоритм Шора, используя возможности квантовых компьютеров, способен произвести факторизацию числа не просто за полиномиальное время, а за время, ненамного превосходящее время умножения целых чисел. Таким образом, с помощью этого алгоритма (при использовании квантового компьютера с несколькими тысячами логических кубитов) становится возможным взлом криптографических систем с открытым ключом.

• (2)    Алгоритм Гровера [17] позволяет найти нужный элемент базы данных за полиномиальное время, что делает его значительно более эффективным по сравнению с классическими алгоритмами. Это имеет потенциальное применение в таких областях, как поиск в больших базах данных, оптимизация и распознавание образов.

• (3)    Квантовые компьютеры могут обрабатывать большие матрицы, а также ускорять различные операции линейной алгебры, значительно улучшая традиционные приложения машинного обучения [3]. В частности, было показано, что при использовании методов квантового машинного обучения можно достичь улучшения производительности (увеличение значений метрик или скорости работы) по сравнению с классическими методами, в том числе и для решения задачи обнаружения вторжений в сетях SDN [18,19].

2.    Методы квантового машинного обучения

Рассмотрим основные методы квантового машинного обучения в сравнении с их классическими аналогами.

K-ближайших соседей (kNN) — это алгоритм классификации, состоящий из трех шагов: вычисление расстояния относительно обучающих элементов; нахождение k элементов, ближайших к тестовому экземпляру; предсказание метки класса посредством голосования большинства.

В квантовом kNN вначале все элементы переводятся в пространство квантовых векторов состояний, затем вычисляются расстояния между классифицируемым объектом и всеми объектами тренировочной выборки с помощью, например, евклидовой метрики [20] , SWAP-теста [21] или других. Далее класс присваивается объекту по большинству, находящемуся в числе его ближайших соседей, как и в классическом kNN. Благодаря свойству суперпозиции кубитов все расстояния от обучающих элементов вычисляются одновременно (квантовый параллелизм), что дает большой прирост к скорости работы алгоритма [20] .

Метод опорных векторов (SVM) с помощью функции-ядра переводит выборку в пространство более высокой размерности, в котором данные становятся линейно разделимыми по классам, и проводит между ними разделяющую гиперплоскость. Квантовый SVM работает схожим образом: сначала происходит кодирование данных в квантовое пространство, затем к ним применяется квантовое ядро для перевода в пространство большей размерности, после чего проводится разделяющая гиперплоскость и выполняется классификация. В качестве методов оптимизации может выступать алгоритм Гровера [22] или алгоритм HHL [23] , которые используют квантовый параллелизм и дают существенный прирост в скорости работы [24] .

В квантовых сверточных нейронных сетях (QCNN) [25] изображение сначала кодируется в квантовую схему с использованием карты признаков. Затем к закодированному изображению применяются чередующиеся сверточные и объединяющие слои, уменьшая размерность схемы до тех пор, пока не останется только один кубит. Выход этого оставшегося кубита измеряется для классификации входного изображения. Квантовый сверточный слой состоит из серии двухкубитных унитарных операторов, которые распознают и определяют связи между кубитами в схеме; квантовый pooling-слой уменьшает количество кубитов, выполняя операции над каждым кубитом до определенной точки, а затем отбрасывая определенные кубиты в определенном слое. В QCNN каждый слой содержит параметризованные схемы, что означает, что выход может быть изменен путем настройки параметров каждого слоя. Во время обучения эти параметры корректируются для минимизации функции потерь.

Метод VQC (variational quantum circuit), использованный в данной работе, наиболее популярен у исследователей. Концептуально его показывает в виде схемы рисунок 2 , навеянный рисунком 13 из [3] . Метод VQC представляет собой квантовый аналог нейронной сети. На входе квантовой

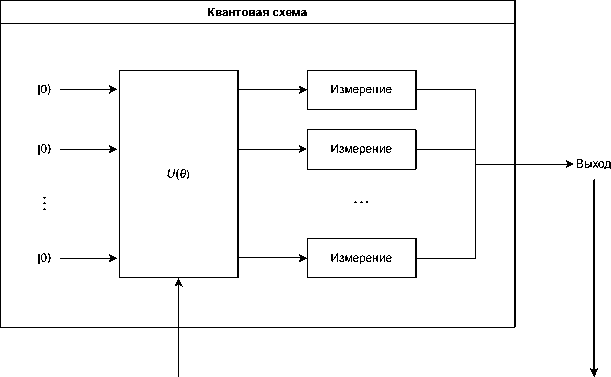
Обновление                                                       Целевая весов                                                         функция

Рисунок 2. Представление метода VQC схемы (Quantum circuit) расположено некоторое количество кубитов, соответствующее количеству признаков в наборе данных, а на выходе формируется решение задачи (например, вероятностное распределение для задачи классификации). Предварительно переведенные в пространство квантовых векторов (с помощью карты признаков) данные поступают на вход этой схеме, после чего она «обучается». Процесс обучения происходит с задействованием классического компьютера: на нем рассчитывается функция потерь и обновляются веса для квантовой схемы, после чего квантовая схема снова начинает работу.

3.    Набор данных

В данной работе используется набор данных InSDN [7] , опубликованный в 2020 году и содержащий различные виды трафика, актуального на сегодняшний день (YouTube, чаты, электронная почта и др.) и характерного для ПКС. Набор данных содержит типы сетевого трафика, представленные в таблице 1. Набор данных несбалансирован, поэтому для балансировки набора данных в некоторых экспериментах использовался алгоритм SMOTE (Synthetic Minority Over-sampling Technique), основная идея которого — генерация искусственных объектов в наборе данных, «похожих» на существующие, но не дублирующих их [26, 27] .

Таблица 1. Виды трафика в наборе данных InSDN

Тип трафика	Количество записей
Нормальный	68424
Атака BFA	1405
Атака DDoS	121942
Атака DoS	53616
Атака Probe	98129
Атака Web-Attack	192
Атака BOTNET	164
Атака U2R	17

Учитывая, что для симуляции квантовых методов машинного обучения на классическом компьютере требуются значительные ресурсы, количество признаков в наборе данных было сокращено с 48 исходных до 10 с помощью функционала SelectKBest из библиотеки Scikit-Learn.

Оставшиеся признаки для экспериментов с задачей бинарной классификации: Protocol, Fwd Pkt Len Min, Bwd Pkt Len Min, Bwd Pkt Len Mean, Bwd Pkt Len Std, Fwd IAT Tot, Pkt Len Min, Pkt Len Mean, Pkt Len Std, Pkt Size Avg.

Оставшиеся признаки для экспериментов с задачей многоклассовой классификации: Protocol, Bwd Pkt Len Min, Bwd Pkt Len Mean, Bwd Pkt Len Std, Flow Pkts/s, Bwd Pkts/s, Pkt Len Min, Pkt Len Mean, Pkt Len Std, Pkt Size Avg.

Помимо сокращения количества признаков набор данных также был разделен на 3000 порций, и на вход методу VQC подавалось по одной порции за раз для минимизации использования памяти. Это тоже повлияло на значение метрики, поскольку качество модели, обучаемой на полном наборе данных, как правило, выше, чем для модели, обучаемой на том же наборе, но порционно.

4.    Эксперименты и результаты

В процессе работы были проведены эксперименты с моделью квантового машинного обучения VQC и моделью классического машинного обучения XGBoost для сравнения. Эксперименты проводились на машине со следующими характеристиками: процессор Intel Xeon E5-2695 v2, 32 Гб оперативной памяти, ОС Windows 10.

Результаты работы моделей представлены в таблице 2. Модель XGBoost была взята как эталон, поскольку метод градиентного бустинга показывает лучшие результаты классификации табличных данных в большинстве случаев.

Для каждой модели было проведено 6 экспериментов:

• (1 )    Бинарная классификация (нормальный или атакующий трафик).

• (2)    Бинарная классификация (нормальный или атакующий трафик) с предварительной нормализацией набора данных с помощью метода минимакс.

• (3 )    Бинарная классификация (нормальный или атакующий трафик) с предварительной нормализацией набора данных с помощью метода минимакс и балансировкой с помощью метода SMOTE.

• (4 )    Многоклассовая классификация (нормальный трафик или один из нескольких типов атак).

• (5 )    Многоклассовая классификация (нормальный трафик или один из нескольких типов атак) с предварительной нормализацией набора данных с помощью метода минимакс.

• (6 )    Многоклассовая классификация (нормальный трафик или один из нескольких типов атак) с предварительной нормализацией набора данных с помощью метода минимакс и балансировкой с помощью метода SMOTE.

Реализация модели VQC взята из библиотеки Qiskit Machine Learning для языка Python, также в работе были использованы инструменты из библиотеки Qiskit 1. Модель VQC была взята с параметрами по умолчанию, в качестве метода оптимизации используется COBYLA

(Constrained Optimization By Linear Approximation optimizer), в качестве карты признаков использована ZZFeatureMap

, в качестве квантовой

схемы использована RealAmplitudes . Модель XGBoost была взята из одноименной библиотеки XGBoost с параметрами по умолчанию.

Для оценки качества моделей были использованы меры accuracy и F1. Значение accuracy есть отношение количества правильно классифицированных объектов к общему количеству элементов выборки, а значение F1-меры сочетает в себе две другие функции оценки качества: precision (доля объектов, действительно принадлежащих данному классу относительно всех объектов, которые модель отнесла к этому классу) и recall (доля найденных классификатором объектов, принадлежащих классу, относительно всех объектов этого класса), что облегчает понимание, насколько качественно работает модель.

Для запуска экспериментов для модели VQC не был использован квантовый компьютер, все вычисления выполнялись с помощью симуляции квантовой архитектуры на классическом компьютере. Из-за этого появились ограничения по скорости работы моделей и используемой памяти: было принято решение сократить количество признаков (как уже говорилось в разделе «набор данных») и сам набор данных разделить на небольшие части и дообучать модель итеративно. Перечисленные ограничения сказались на времени обучения модели (как мы видим, оно на несколько порядков выше по сравнению с классическим методом) и значениях метрик.

Модель XGBoost обучалась также на наборе данных с сокращенным количеством признаков, но на всем наборе данных целиком, а не порциями, поскольку градиентный бустинг не поддерживает механизм дообучения и требует на вход полный набор данных за раз.

Из результатов экспериментов мы видим, что нормализация набора данных приводит к увеличению значений метрик VQC, а также балансировка набора данных методом SMOTE в эксперименте с многоклассовой классификацией, поскольку в этом случае присутствует несколько классов, представленных крайне малым количеством объектов. Нормализация не оказывает сильного влияния на классический метод XGBoost в силу особенностей его архитектуры, а балансировка набора данных не увеличивает значения метрик для обеих моделей в эксперименте с бинарной классификацией, поскольку в этом случае оба класса представлены достаточным количеством объектов.

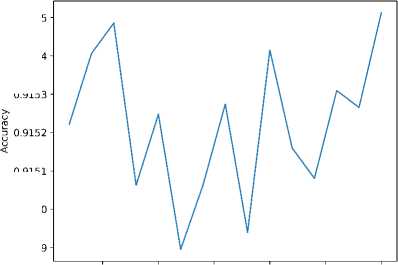
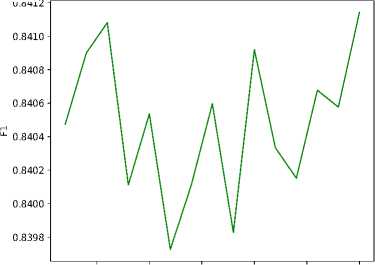
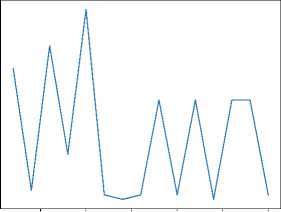
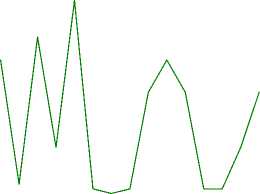
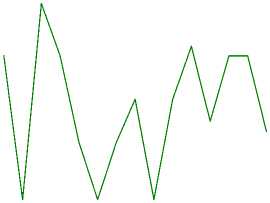
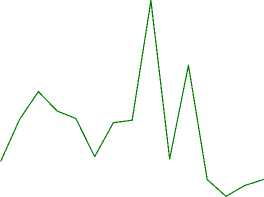
Для экспериментов с нормализацией и балансировкой набора данных приведем графики, отражающие динамику изменения значений метрик во время обучения модели VQC по порциям (рисунки 3 и 4) . Среди результатов экспериментов особое внимание хочется обратить на значения accuracy в экспериментах с бинарной классификацией (выделены жирным шрифтом в таблице 2) .

Таблица 2. Результаты экспериментов

Эксперимент	VQC			XGBoost
	Accuracy	F1-мера	время работы	Accuracy	F1-мера	время работы
Бинарная классификация	0,771	0,656	721985 с	0,982	0,970	1,622 с
- она же после минимакс	0,916	0,841	722345 с	0,982	0,970	1,639 с
- она же после минимакс и SMOTE	0,915	0,841	954277 с	0,980	0,968	7,703 с
Многоклассовая классификация	0,423	0,170	835228 с	0,976	0,824	26,068 с
- она же после минимакс	0,480	0,201	836823 с	0,976	0,824	22,133 с
- она же после минимакс и SMOTE	0,624	0,210	984248 с	0,958	0,702	81,959 с

0.9155

0.9154

0.9153

0.9152

0.9151

0.9150

0.9149

Номер порции

Рисунок 3. Динамика изменения метрик accuracy и F1 во время обучения модели VQC в экспериментах с бинарной классификацией на нормализованных данных

Номер порции

14                      И. А. Антонов, И. И. Курочкин

Бинарная классификация (+SMOTE)

0.91550

0.91545

0.91540

g- 0.91535

0.91530

0.91525

0.91520

0.91515

500      1000     1500     2000     2500     3000

Номер порции

Бинарная классификация (+SMOTE)

0.8410

0.8408

0.8406

0.8404

500     1000     1500     2000     2500     3000

Номер порции

Многоклассовая классификация

Многоклассовая классификация

0.220

0.215

0.210

0.205

0.200

0.195

0.190

500     1000     1500     2000     2500     3000

Номер порции

500     1000     1500     2000     2500     3000

Номер порции

0.6400

0.6375

0.6350

0.6325

0.6300

0.6275

0.6250

0.6225

Многоклассовая классификация (+SMOTE)

500      1000     1500     2000     2500     3000

Номер порции

0.213

0.208

Многоклассовая классификация (+SMOTE)

0.212

0.211

0.210

0.209

500     1000     1500     2000     2500     3000

Номер порции

Рисунок 4. Динамика изменения метрик accuracy и F1 во время обучения модели VQC в экспериментах на нормализованных данных

Пока результат работы квантового метода VQC хуже, чем эталонного для задачи XGBoost, но мы видим, что уже получается приблизиться к эталону, результаты работы моделей сопоставимы. При будущих доработках квантовых компьютеров вполне возможно, что квантовые методы смогут превзойти классические, как по значениям метрик, так и по скорости работы.

Заключение

Проведенная работа показала, что квантовые методы машинного обучения уже сейчас можно ограниченно применять и исследовать. На данный момент они требуют гораздо больше ресурсов для симуляции на классическом компьютере, чем привычные нам классические методы, но при большем распространении квантовых компьютеров и увеличении числа кубитов в них QML-методы смогут составить конкуренцию традиционным ML-моделям (а возможно и превзойти их) благодаря квантовому параллелизму и существенному увеличению скорости работы. По этой причине уже сейчас необходимо изучать их, в частности, применительно к задаче обнаружения вторжений в сетях SDN, поскольку в будущем СОВ на основе методов квантового машинного обучения вероятно смогут анализировать гораздо большие объемы информации с большей скоростью, что сделает их значительно эффективнее, чем традиционные IDS.

В данной работе проведен ряд экспериментов для метода квантового машинного обучения VQC и показано, что он может достигать результатов, сопоставимых с классическим методом градиентного бустинга, который является эталоном для задачи классификации табличных данных. При запуске модели VQC на квантовом компьютере, а не в симуляции, можно получить и прирост в скорости работы, помимо приемлемых результатов метрик.

Полученный в работе результат не является конечным, можно выделить два направления исследований для его улучшения. Во-первых, можно улучшать производительность текущей модели VQC путем подбора гиперпараметров и дополнительной предобработки данных. Во-вторых, можно рассмотреть и другие методы квантового машинного обучения, такие как QSVM, квантовые нейронные сети, гибридные квантово-классические архитектуры. Движение в обоих направлениях может привести к более эффективному решению задачи обнаружения вторжений в программно-конфигурируемых сетях.