Методы многомерной сплайн-интерполяции-экстраполяции для аппроксимации гидравлических характеристик элементов рулевых машин ракетных блоков

Автор: Белоногов Олег Борисович

Журнал: Космическая техника и технологии @ktt-energia

Рубрика: Системный анализ, управление и обработка информации

Статья в выпуске: 1 (28), 2020 года.

Бесплатный доступ

В статье рассматриваются принципы создания методов многомерной аппроксимации гидравлических характеристик дроссельных окон золотниковых гидрораспределителей электрогидравлических усилителей рулевых машин, в основу которых была положена кубическая сплайн-интерполяция-экстраполяция (СИЭ) зависимостей. Отличительная особенность разработанных методов заключается в том, что при математическом моделировании сложные аналитические зависимости характеристик не требуются, а для их аппроксимации в процессе расчетов используются только табличные представления экспериментальных данных. Представленные в настоящей работе многомерные методы аппроксимации, основанные на кубической СИЭ, прошли апробацию в математических моделях статического анализа автономных однокаскадных электрогидравлических рулевых машин с двух - и четырехдроссельным электрогидравлическими усилителями и показали свою высокую эффективность. Благодаря им погрешность расчета статических характеристик рулевых машин в широких диапазонах температуры рабочей жидкости и напряжения питания в настоящее время не превышает ±2%.

Еще

Метод многомерной аппроксимации, кубическая сплайн-интерполяция- экстраполяция, электрогидравлическая рулевая машина

Короткий адрес: https://sciup.org/143177918

IDR: 143177918 | DOI: 10.33950/spacetech-2308-7625-2020-1-119-125

Текст научной статьи Методы многомерной сплайн-интерполяции-экстраполяции для аппроксимации гидравлических характеристик элементов рулевых машин ракетных блоков

Для создания итерационных методов расчета безразмерных параметров течений потоков жидкости в дроссельных окнах золотниковых гидрораспределителей (ГР) электрогидравлических усилителей (ЭГУ) [1–3], в зазорах предохранительных и переливных клапанов [4], а также в соединительных каналах и трубопроводах [5] рулевых машин (РМ), необходимо располагать точными аппроксимирующими характеристиками зависимостей гидравлических параметров от одного, двух или трех безразмерных факторов.

В большинстве случаев эти зависимости носят сложный нелинейный или трансцендентный характер, и до недавнего времени для их аппроксимации авторами создавались достаточно сложные аналитические модели [6, 7] даже для одномерных зависимостей. С развитием компьютерной техники появилась возможность аппроксимировать такие зависимости с помощью метода кубической сплайн–интерполяции–экстраполяции (СИЭ), однако его внедрение в моделирование гидравлических характеристик составляющих элементов гидроприводов долгое время сдерживалось низким уровнем быстродействия вычислительной техники. Отличительная особенность данного метода заключается в том, что аналитические зависимости характеристик не требуются, а в расчетах статических или динамических характеристик РМ по соответствующим математическим моделям используются табличные представления экспериментальных данных.

Описание методов, алгоритмов и программ кубической СИЭ для одномерных табличных зависимостей представлено в работах [8, 9].

Стремительное развитие вычислительной техники и совершенствование ее характеристик (в частности, возрастание уровня ее быстродействия) позволяют практически полностью переориентировать аналитические методы аппроксимации на методы кубической СИЭ, однако методы кубической СИЭ для многомерных табличных зависимостей остаются неразвитыми.

В связи с этим определенный теоретический и практический интерес представляет задача разработки многомерных методов кубической СИЭ для аппроксимации многомерных зависимостей.

Принципы создания таких многомерных методов рассмотрим на примере аппроксимации зависимостей коэффициента расхода µ сливного дроссельного окна сегментной формы двухдроссельного золотникового ГР ЭГУ РМ от числа Рейнольдса Re, фактора вращения гильзы Ψ и относительного противодавления на выходе дроссельного окна ^– p , приведенных в табл. 1 [3].

Таблица 1

Значения коэффициента расхода µ при различных значениях числа Рейнольдса Re, фактора вращения Ψ и относительного противодавления на выходе р ^–

Re	^µ
	_– p = 0				^^^^^ p = 0,2				_– p = 0,4
	Ψ = 0,00	Ψ = 0,33	Ψ = 0,66	Ψ = 0,99	Ψ = 0,00	Ψ = 0,33	Ψ = 0,66	Ψ = 0,99	Ψ = 0,00	Ψ = 0,33	Ψ = 0,66	Ψ = 0,99
10	0,490	0,491	0,492	0,490	0,490	0,491	0,492	0,490	0,490	0,491	0,492	0,490
20	0,592	0,593	0,600	0,613	0,592	0,593	0,600	0,610	0,592	0,593	0,600	0,610
30	0,638	0,645	0,651	0,653	0,642	0,650	0,656	0,672	0,642	0,650	0,658	0,668
40	0,664	0,672	0,680	0,670	0,674	0,684	0,693	0,710	0,678	0,688	0,697	0,707
50	0,680	0,690	0,688	0,680	0,700	0,710	0,721	0,738	0,700	0,710	0,720	0,738
60	0,693	0,702	0,700	0,684	0,721	0,730	0,740	0,750	0,721	0,730	0,743	0,752
70	0,705	0,710	0,702	0,688	0,732	0,742	0,752	0,756	0,740	0,748	0,761	0,766
80	0,711	0,717	0,706	0,690	0,743	0,752	0,764	0,758	0,755	0,762	0,778	0,770
90	0,720	0,720	0,708	0,692	0,753	0,762	0,773	0,760	0,767	0,776	0,783	0,776
100	0,726	0,725	0,709	0,693	0,762	0,771	0,779	0,762	0,780	0,790	0,790	0,780
200	0,750	0,728	0,705	0,690	0,801	0,800	0,780	0,764	0,833	0,815	0,800	0,792
300	0,748	0,715	0,696	0,684	0,800	0,785	0,772	0,760	0,829	0,808	0,793	0,786
400	0,738	0,707	0,688	0,678	0,790	0,776	0,764	0,758	0,815	0,808	0,787	0,781
500	0,725	0,700	0,683	0,677	0,787	0,772	0,761	0,757	0,810	0,808	0,786	0,780
600	0,714	0,693	0,680	0,673	0,787	0,772	0,761	0,756	0,780	0,808	0,786	0,780
800	0,705	0,688	0,678	0,670	0,787	0,772	0,761	0,756	0,808	0,808	0,786	0,780
1 000	0,703	0,687	0,677	0,670	0,787	0,772	0,761	0,756	0,807	0,808	0,786	0,780
3 000	0,700	0,687	0,677	0,670	0,787	0,772	0,761	0,756	0,807	0,808	0,786	0,780
10 000	0,700	0,687	0,677	0,670	0,787	0,772	0,761	0,756	0,807	0,808	0,786	0,780

Метод двухмернойсплайн–интерполяции–экстраполяции

Для пояснения метода двухмерной аппроксимации, основанной на кубической СИЭ, рассмотрим зависимости коэффициента расхода дроссельного окна µ от числа Рейнольдса Re и фактора вращения гильзы Ψ, представленные в табличной форме (фрагмент табл. 1 при значении относительного противодавления на выходе ^– p = 0) (рис. 1).

Допустим, нам требуется определить значение коэффициента расхода µ при Ψ = 0,5 и Re = 150.

Алгоритм метода двухмерной аппроксимации для определения коэффициента расхода μ предписывает выполнение следующей последовательности действий:

1. для каждой строки табл. 1 при p = 0 с помощью одномерного метода кубической СИЭ определяются значения коэффициента расхода µ, т. е. µ = spl (Ψ)
2. по полученным расчетным данным формируется массив данных, иллюстрируемый табл. 2;

при Ψ = 0,5, что, как пример, для строки Re = 300 иллюстрируется графиком рис. 2 (μ = 0,7036);

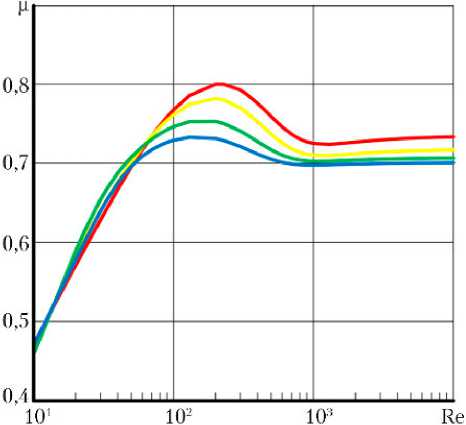
Рис. 1. Графики зависимостей коэффициента расхода µ от числа Рейнольдса Re и фактора вращения Ψ при ^–p = 0:

— - Т = 0,00; — - Т = 0,33; — - Т = 0,66; — - Т = 0,99

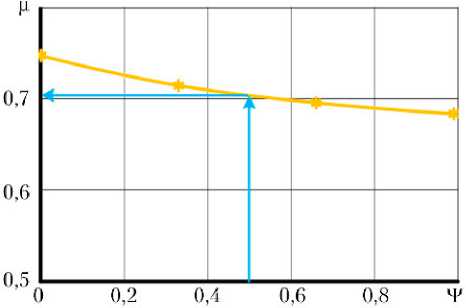
Рис. 2. График зависимости коэффициента расхода µ от фактора вращения гильзы Ψ при числе Рейнольдса Re = 300 и относительном противодавлении на выходе дроссельного окна ^–p = 0

Таблица 2

Зависимость полученных значений коэффициента расхода µ от числа Рейнолдса Re

Re	^μ	Re	^μ	Re	^μ
10	0,490	80	0,713	600	0,685
20	0,595	90	0,715	800	0,682
30	0,648	100	0,717	1 000	0,681
40	0,677	200	0,715	3 000	0,681
50	0,691	300	0,703	10 000	0,686
60	0,702	400	0,695	_—	_—
70	0,707	500	0,690	_—	_—

3. по данным табл. 2 с помощью одномерного метода кубической СИЭ определяется значение µ = spl (Re) при Re = 150, что иллюстрируется рис. 3.

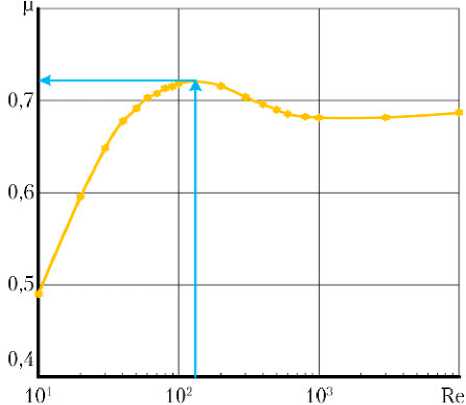
Рис. 3. График зависимости коэффициента расхода µ от числа Рейнольдса Re при значении фактора вращения гильзы Ψ = 0,5

Функцию двухмерной аппроксимации коэффициента расхода µ удобно определить функцией двухмерной кубической СИЭ: µ = spl (Ψ; Re).

В результате получаем искомое значение µ = spl (0,5; 150) = 0,7226.

Метод трехмернойсплайн–интерполяции–экстраполяции

Для пояснения метода трехмерной СИЭ рассмотрим зависимости коэффициента расхода дроссельного окна μ от числа Рейнольдса Re и фактора вращения гильзы Ψ, представленные в табл. 1, при значениях относительного противодавления на выходе дроссельного окна ^– p = 0; 0,2 и 0,4, которые иллюстрируются рис. 1 и 4 [3].

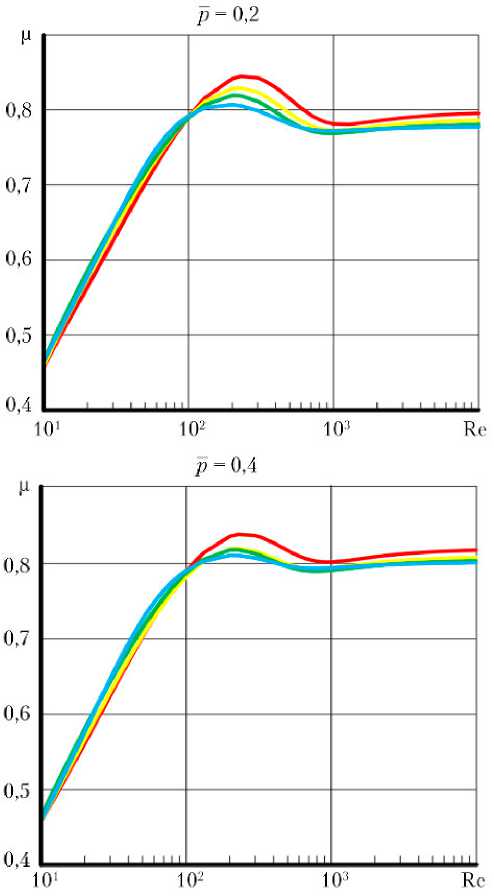
Рис. 4. Графики зависимостей коэффициента расхода µ от числа Рейнольдса Re и фактора вращения гильзы Ψ при относительном противодавлении на выходе дроссельного окна p = 0,2 и 0,4: — — Т = 0,00; — — Т = 0,33; — — Т = 0,66; — — Т = 0,99

Допустим, нам требуется определить значение коэффициента расхода μ при Ψ = 0,5; Re = 150 и ^– p = 0,25.

Алгоритм метода трехмерной аппроксимации для определения коэффициента расхода µ предписывает выполнение следующей последовательности действий:

1. выполняется двухмерная аппроксимация, основанная на кубической СИЭ, для каждого фрагмента табл. 1 при ^– p = 0; 0,2 и 0,4 по определению µ = spl (Re; Ψ) при Re = 150 и Ψ = 0,5 вышеприведенным методом;
2. по полученным данным формируется массив данных, иллюстрируемый табл. 3;
3. по данным табл. 3 с помощью одномерного метода кубической СИЭ определяется значение μ, т. е. μ = spl (^– p ) при ^– p = 0,25 (рис. 5).

Таблица 3

Зависимость полученных значений коэффициента расхода µ от относительного противодавления на выходе p

– _p	0	0,2	0,4
^μ	0,190	0,490	0,638

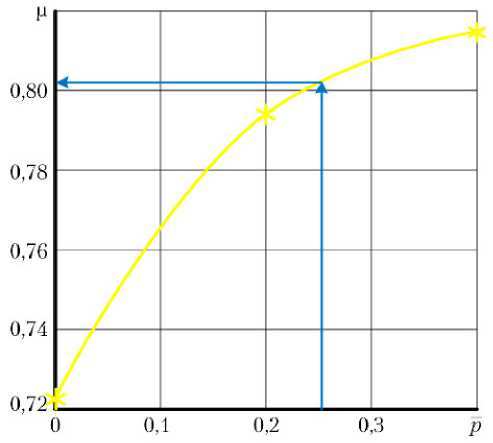
Рис. 5. График зависимости коэффициента расхода µ от относительного противодавления на выходе ^–p при значении фактора вращения гильзы Ψ = 0,5 и числе Рейнольдса Re = 150

Функцию трехмерной аппроксимации коэффициента расхода µ удобно определить функцией трехмерной кубической СИЭ: µ = spl (Re; Ψ; ^– p ).

В результате получаем искомое значение µ = spl (150; 0,5; 0,25) = 0,8023.

Очевидно, что, действуя аналогичным образом, можно сколь угодно увеличивать размерность разработанных методов аппроксимации. В связи с неравномерным (логарифмическим) разбиением интервала аппроксимации на отрезки необходимо на каждом этапе проводить визуальную оценку гладкости получаемых аппроксимационных характеристик.

Представленные в настоящей работе многомерные методы аппроксимации, основанные на кубической СИЭ, прошли апробацию в виде соответствующих процедур в математических моделях статического анализа автономных однокаскадных электрогидравлических РМ с двух- и четырехдроссельным ЭГУ [10, 11], в процедурах моделирования углов истечения потоков рабочей жидкости в дроссельных окнах золотниковых ГР ЭГУ РМ [1] и в процедурах моделирования зависимостей физических свойств рабочих жидкостей РМ от температуры, давления, а также некоторых других факторов [12], и показали свою высокую эффективность. Благодаря этому погрешность расчета статических характеристик РМ в широких диапазонах температуры рабочей жидкости и напряжения питания в настоящее время не превышает по модулю 2% [10, 11].

Заключение

Разработаны и предложены методы многомерной аппроксимации гидравлических характеристик дроссельных окон золотниковых гидрораспределителей электро-гидравлических усилителей рулевых машин, в основу которых была положена кубическая сплайн–интерполяция–экстра-поляция зависимостей.

Разработанные методы многомерной СИЭ для аппроксимации гидравлических характеристик элементов рулевых машин прошли апробацию в математических моделях статического анализа автономных однокаскадных электрогидравлических рулевых машин с двух- и четырехдроссельным электрогидравлическими усилителями, в процедурах моделирования углов истечения потоков рабочей жидкости в дроссельных окнах золотниковых гидрораспределителей рулевых машин, в процедурах моделирования зависимостей физических свойств рабочих жидкостей рулевых машин от температуры, давления, а также некоторых других факторов, и показали свою высокую эффективность.

Список литературы Методы многомерной сплайн-интерполяции-экстраполяции для аппроксимации гидравлических характеристик элементов рулевых машин ракетных блоков

Белоногое О.Б. Экспериментальные исследования и идентификация углов истечения потоков в дроссельных окнах золотниковых гидрораспределителей рулевых машин ракет // Вестник МГТУ им. Н.Э. Баумана. Сер. «Машиностроение». 2015. № 1. С. 35-48.
Белоногое О.Б. Экспериментальные исследования и метод идентификации безразмерных параметров течения потоков жидкости в дроссельных окнах золотниковых гидрораспределителей // Вестник МГТУ им. Н.Э. Баумана. Сер. «Машиностроение». 2015. № 3. С. 43-57.
Белоногое О.Б. Экспериментальные исследования истечения и безразмерных параметров течения потоков жидкости в дроссельных окнах золотниковых гидрораспределителей с вращающимися гильзами // Вестник МГТУ им. Н.Э. Баумана. Сер. «Машиностроение». 2016. № 5. С. 4-23.
Белоногое О.Б. Метод идентификации безразмерных параметров течения потоков жидкости в шариковых предохранительных и переливных клапанах рулевых машин ракет и двигательных установок космических аппаратов // Вестник НПО им. С.А. Лавочкина. 2015. № 1. С. 66-70.
Белоногое О.Б., Жарков М.Н., Кудрявцев В.В., Шутенко В.И. Итерационный метод расчета параметров течений рабочей жидкости в соединительных трубопроводах, каналах, проточных элементах и клапанах // Ракетно-космическая техника. Труды. Сер. XII. Королёв: РКК «Энергия», 1997. Вып. 1. С. 97-106.
McCloy D. Discharge characteristics of servo valve orifices // Fluid Power International Conference, Olympia, 1968. P. 43-50.
Weule H. Eine Durchflussgleichung fur den laminar-turbulenten Stromungsbereich // Olhydraulik und Pneumatik. 1974. V. 18. № 1. S. 57-67.
Дьяконое В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ. М.: Наука, 1989. 24G с.
Фароное В.В. Программирование на персональных ЭВМ в среде Турбо-Паскаль. М.: Изд-во МГТУ, 1991. 58G с.
Белоногое О.Б. Итерационные методы статического анализа двухдрос-сельной электрогидравлической рулевой машины ракетных блоков // Космическая техника и технологии. 2G18. № 2(21). С. 93-105.
Белоногое О.Б. Итерационные методы статического анализа четырехдрос-сельной электрогидравлической рулевой машины ракетных блоков // Космическая техника и технологии. 2G19. № 2(25). С. 115-126. DOI 10.33950/spacetech-2308-7б25-2019-2-115-12б.
Белоногое О.Б., Жаркое М.Н., Кристальный С.Р., Кудряецее В.В., Шутенко В.И. Моделирование физических свойств рабочих жидкостей рулевых машин и гидроприводов // Ракетно-космическая техника. Труды. Сер. XII. Королёв: РКК «Энергия», 1997. Вып.1. С. 107-117.

Еще

Статья научная