Методы оценивания параметров кривой логистического роста. Ч. 1. Оптимизация условий оценивания при наличии аддитивной случайной помехи

Основам осуществления полимеразной цепной реакции (ПЦР) посвящено множество работ, в частности [1–6]. Ранее было доказано, что информативный сигнал в приборах, реализующих полимеразную цепную реакцию в реальном масштабе времени, в первом приближении описывается кривой логистического роста. Даже предложенные альтернативные модели трехстадийной динамики (практическое отсутствие роста количества ДНК, экспоненциальный (геометрический) рост и выход на стадию насыщения) [7, 8] не противоречат на качественном уровне гипотезе о логистическом росте.

Одной из принятых форм этой кривой является

X = X *

n 1 + ( B - 1) a 0 n

.

Здесь Х n — величина сигнала на n -м шаге измерения ( n = 0, 1,…, N , где N обычно 30–40).

Подобная форма зависимости получается с помощью квантования по времени (дискретизации) решения задачи Коши d x /d t = Ax (1 - x / x *); x (0) = x0.        (2)

Соответствующее дифференциальное уравнение первого порядка есть уравнение Бернулли (см., например, [9]) Оно решается в квадратурах отно- сительно y = x 1(t) при любых зависимостях от времени параметров A = A(t); x* = x*(t). В частности, в работе [10] рассмотрены формы решений уравнения (2) при линейных зависимостях параметров уравнения от времени.

Определяющими параметрами являются следующие.

• 1)    Коэффициент a 0 , обычно находящийся в пределах 1.78–1.98 (при теоретическом пределе, равном 2), характеризующий эффективность проведения реакции. Этот коэффициент определяет средний прирост количества ДНК за 1 цикл.

• 2)    Величина Х ^* характеризует максимальный информативный сигнал, т. е. либо величину сигнала при максимальном количестве ДНК (при достижении режима насыщения), либо максимально допустимую величину сигнала, определяемую чувствительностью измерения, разрядностью устройств (в частности, АЦП) и другими факторами, связанными не с ПЦР, а с выбранным режимом измерения.

• 3)    Параметр В численно равен отношению Х ^* и Х 0 — сигнала, соответствующего начальному (достаточно малому) количеству ДНК. Соответствующее отношение В обычно не менее 10³, но может достигать 10⁶–10⁷.

Основные особенности рассматриваемых информативных сигналов.

• 1)    Наличие аддитивной помехи, которую будем полагать ограниченной в диапазоне ± 5 (возможно, от единиц до 10–20 отсчетов).

• 2)    Максимальный сигнал Х полагаем превосходящим 1000 (возможно, до 3000–4000 отсчетов). Эта величина, в частности, определяется разрядностью используемого АЦП.

• 3)    Сигнал, соответствующий начальному количеству ДНК Х 0 , как правило, не превосходит 1 отсчета (возможно, 10^–3 и менее).

Главные методические проблемы анализа информативных сигналов состоят в следующем:

• а)    значимые параметры Х ^* и a 0 априорно неизвестны, а величина Х 0 по существу и является искомой аналитической информацией;

• б)    при определенных условиях анализа кривая может не достигать стадии насыщения;

• в)    калибровка прибора обычно осуществляется на основе наиболее устойчивой комплексной характеристики сигнала — так называемого порогового цикла, т. е. стадии анализа, когда информативный сигнал обладает наибольшей линейностью. Аналитически положение порогового цикла может быть вычислено из соотношения n * = ln( B - 1) / ln( a 0 ). При этом следует учесть, что n ^* необходим для определения В . Например, если при a 0 = 2 пороговый цикл равен 20.00, то этому значению В при a 0 = 1.8 будет соответствовать сильное смещение положения порогового цикла до 23.58. Таким образом, при осуществлении калибровки по положению порогового цикла n ^* необходимо учитывать и эффективность ПЦР (т. е. величину a 0 ).

Дальнейшие рассуждения касаются реализации алгоритмов последовательного оценивания базовых параметров информативного сигнала ( a 0 , Х , а также Х 0 или/и n ^*).

НАЧАЛЬНЫЕ УСТАНОВКИ АЛГОРИТМА.

ОСНОВНЫЕ ПРИНЦИПЫ ОЦЕНИВАНИЯ ИНФОРМАТИВНЫХ ПАРАМЕТРОВ —

ПОСЛЕДОВАТЕЛЬНОСТЬ, РЕАЛИЗАЦИЯ И КАЧЕСТВО ОЦЕНИВАНИЯ

Полагаем, что информативный сигнал X n содержит аддитивную ограниченную помеху ζ n . (Для конкретизации считаем помеху равномерной и независимой).

Исследуем вторую разность информативного сигнала:

2 Х_п — X_n - 1 — X_n + 1 = 2Z_n — Z n — 1 — Z n + 1 +

+ X *( a 0 - 2 + 1/ a 0 )---------- t ⁽¹ t )----------.

(1 + 1 )(1 + 1 / a ₀)(1 + a 0 1 )

Здесь t = (B -1) / a0’. Исследование экстремумов второй разности (и связанной с ним кривизны) зависимости (3) дает следующие результаты: t = 1 — точка нулевой кривизны (соответствует наиболее линейному участку кривой и положению порогового цикла n = n*); в зависимости от a0 максимальная кривизна кривой реализуется при t, близких к 4 и ¼ (точнее: при a0 = 2 эти значения 4.013 и 0.249, при a0 = 1.9 и менее — 3.87 и 0.26). Практически эти точки отстоят примерно на 2 отсчета от точки перегиба (или порогового цикла).

Ориентировочно оценим максимальную вторую разность в этих и соседних точках. Зададим a 0 = 2, т. к. при достаточно близких значениях параметра результаты будут количественно схожи. Следует отметить, что замена t на 1/ t означает движение по логистической кривой в другую сторону от точки перегиба. Соответствующие величины второй разности в этом случае будут совпадать по модулю и иметь противоположный знак. При t > 1 эти отсчеты предшествуют точке перегиба, и вторая разность отрицательна; при t < 1 рассматриваются отсчеты после точки перегиба или порогового цикла.

Оценим величину второй разности при отсчетах, соответствующих t = 8, 4, 2, т. е. в трех предшествующих пороговому циклу отсчетах (полагаем при этом, что n ^* — целая величина). При дробных n ^* характерные величины второй разности в трех ближайших к пороговому циклу отсчетах будут соответствовать названным величинам t , деленным на a 0 в степени { n ^*} — дробная часть от n ^* — (т. е. на величину от 1 до 2 ).

В отсчетах t = 8, t = 4, t = 2 вторая разность — по абсолютной величине Х ^*/27.32, Х ^*/22.5 и Х ^*/30.0 соответственно. Суммарная аддитивная помеха при формировании второй разности (3) достоверно не превзойдет по величине 4 δ . Тем самым гарантировано, что при условии δ <  X ^*/ 120 по крайней мере в 3 последовательных отсчетах, предшествующих точке перегиба, будет сохраняться знак второй разности. Далее при переходе через точку перегиба произойдет смена знака второй разности с отрицательного на положительный. В указанной ситуации с точностью примерно 0.5 отсчета может быть установлено положение точки перегиба (по интервалу смены знака второй разности).

Более подробно исследуем аддитивную помеху для второй разности. В первом приближении закон распределения помехи каждого измерения Xn полагаем равномерным. В принципе допустимо рассматривать любую гипотезу о распределении случайной составляющей помех при наложенных ограничениях о симметричности (и как следствие центрированности) и ограниченности. При независимости помех на (n – 1), n и (n + 1) отсчетах плотность распределения вероятностей (ПРВ) результирующей помехи получается методом сверт- ки. Удобнее использовать аппарат характеристических функций (см., например, [11]). Переход к характеристическим функциям аналогичен преобразованию Лапласа с заменой аргумента р на мнимый аргумент (jw).

Для равномерной в диапазоне [– δ , δ ] помехи характеристическая функция имеет вид

® * ( jw ) =

1 eijws - e-iw s

2 δ    jw

Результирующей помехе соответствует произведение характеристических функций вида (4), что приводит к выражению:

® ( jw ) =

( e jw2 s - e - jw 2 s )( ejw s

e - ^{jw s} ) 2

( jw )³

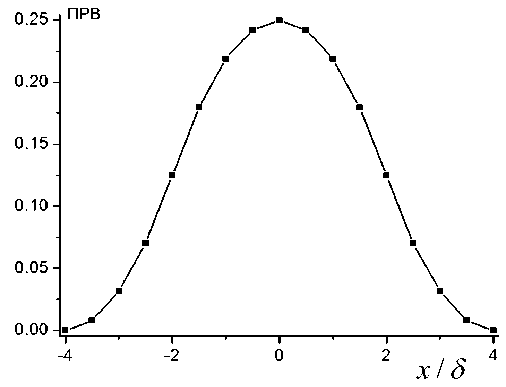
Рис. 1. ПРВ случайной составляющей второго разностного сигнала

Здесь первый множитель соответствует слагаемому 2 ζ n , два других множителя в числителе соответствуют помехам ζ n –1 и ζ n +1 .

Обращение характеристической функции (5) аналогично переходу к оригиналу для преобразования Лапласа позволяет получить выражения для ПРВ в форме

P ^{( x} ) =

= 32 ^ 3 [ ( x + 4 ^{s )2} n( x + 4 ^s ) ^{- 2(} x + 2^{s )2} n ⁽ x + 2^s ) +

+ 2( x - 2 s )² n( x — 2 s ) + ( x - 4 s )² n( x — 4 s ) ] .

Здесь η ( x ) — функция Хевисайда (функция единичного скачка). Обращение характеристической функции можно выполнить либо с использованием таблиц преобразования Лапласа [12], либо на основе теории вычетов. Соответственно для характерных интервалов явное выражение ПРВ примет вид:

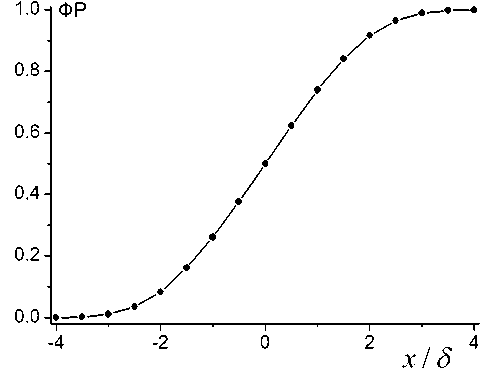
Рис. 2. Функция распределения (ФР) случайной составляющей второго разностного сигнала

x <- 4s :

x e [ - 4 5 , - 2 s ):

x e [ - 2 s ;0]:

P (x) = 0, p (x) = (x + 4s )2/(32s3), p(x) = (8s2 -x2)/(32s3);

V x ^ p ( - x ) = p ( x ).

График ПРВ представлен на рис. 1, а соответствующая функция распределения иллюстрируется рис. 2.

На основе (6) легко рассчитать вероятности попадания суммарной помехи в заданный диапазон значений: вероятность попадания в интервал [0, 1 δ ] равна 23/96, [1 δ , 2 δ ] — 17/96, [2 δ , 3 δ ] — 7/96 и [3 δ , 4 δ ] — 1/96. Математическое ожидание равно нулю, дисперсия как сумма дисперсий 3 независимых слагаемых будет (4+1+1) δ ² /3. Таким образом видно, что подобная суммарная помеха "фокусируется" в окрестности x = 0.

Алгоритмы оценивания информативных параметров сигнала a 0 , X и В базируются на принципе построения постоянного сигнала (тренда нулевого порядка) на основе имеющихся измерений X n при аддитивной случайной помехе ζ n .

На первом этапе строится последовательность оценок величины a 0 в форме

, = ^X n + 2 ( ^X n + 1 - ^X n ) (7) ⁰ X n ( X n + 2 - X n + 1 ). ^U

Указанная схема, учитывающая три последовательных измерения, начиная с отсчета n (далее трехточечная схема), обладает большей алгоритмической простотой, но меньшей точностью. В принципе возможно решение задачи оптимизации выбора базовых отсчетов n, n + 1 и n + 2 по крите- рию минимума дисперсии ошибки определения a0. Соответствующее положение отсчетов должно удовлетворять условию t « 1.7. (Это положение точки оптимума достаточно слабо зависит от измеряемой величины a0). На практике следует учесть, что этот оптимум может реализоваться приближенно, поскольку n должно быть целым.

Более точной схемой для построения оценки величины a ₀ ^k и как следствие a 0 является 4-точечная схема с использованием сигнала в отсчетах n , n + 1, n + k и n + k + 1:

a к = X n + k X n + к + 1 ( X n + 1 - X n ) 0    X n X n + 1 ( X n + к + 1 - X n + к )

Таким образом, используются разделенные на k отсчетов две пары последовательных измерений.

Дисперсия ошибки оценивания (в линейном приближении) зависит от n и k (задача оптимизации по критерию минимума дисперсии решается поиском нетривиального минимума функции 2 переменных t и k ). Положение оптимума также слабо зависит от величины a 0 : при a 0 достаточно больших (1.90 и более) положение оптимума соответствует t « 4.5, к = 4; при менее эффективной ПЦР ( а о ~ 1.80) оптимальными будут условия t ® 5 и k = 5. В принципе незначительное отклонение базовых отсчетов ( n , n + 1, n + k и n + k + 1) от оптимальных слабо влияет на величину дисперсии ошибки оценивания a 0 .

Вторым этапом является определение максимального сигнала Х в соответствии с выражением

- 1

а к / X n + к — 1/ X n "

После вычисления Х ^* имеется возможность оценить ln( В - 1), далее вычислить В или/и положение порогового цикла n ^*. Используются уже выбранные отсчеты со значениями величин сигнала X n :

ln( В - 1) = ln( X */ X_n - 1) + n ln( a ₀).        (10)

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ И ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ ПРОЦЕДУРЫ НАХОЖДЕНИЯ ПАРАМЕТРОВ КРИВЫХ ЛОГИСТИЧЕСКОГО РОСТА

В качестве генератора равномерно распределенной случайной величины использована программа RANDOM на языке С++. Генерация соответствующей случайной величины с диапазоном [- 8 , 8 ] выполнена как

2 5 (RANDOM(1001) /1000 - 1/ 2).

В круглых скобках показан способ генерации равномерно распределенной центрированной случайной величины в диапазоне [–0.5, 0.5].

Далее представлены результаты имитационного моделирования расчета параметров информативного сигнала. Заданы следующие параметры информативного сигнала и случайной помехи: a 0 = = 1.920; X = 3500; X 0 = 0.02; δ = 10. Этим параметрам соответствует n ^* = 18.507; B = 174999 .

По критерию смены знака второй разности выявлено положение порогового цикла на интервале 18–19 отсчетов. Выбрана 4-точечная схема (8) для оценивания a 0 : k = 4 и n = 13–18. Значению n = 13 соответствует t = 41.5 (исходя из предположения, что a 0 = 1.9), т. е. этот отсчет примерно на 3–4 такта предшествует оптимальному режиму оценивания a 0 .

6 оценок a 0 равны: 1.918, 1.896, 1.918, 1.906, 1.917, 1.927. Результирующая оценка 1.917. На основе этих же измерений получены, согласно (9), оценки X ^*: 3395, 3385, 3491, 3490, 3504, 3505, и итоговая оценка 3490.2, а также оценки (10) величины ln( В - 1): 12.029, 12.031, 12.042, 12.045, 12.038, 12.051. На базе результирующей оценки ln( В - 1) получено В = 169388 и как следствие — X 0 = 0.0206; n ^* = 18.497. Все оценки значения достаточно близки к заданным значениям.

Оценки параметров вычислялись на основе различных базовых измерений вблизи области оптимальных значений ( n , k ). В качестве результирующей оценки была использована медиана выборки 6 измерений, т. е. полусумма 2 центральных порядковых статистик. Как известно, она обладает робастностью и одновременно с этим учитывает и различие оценок, полученных на основе разных отсчетов. Далее будет рассмотрена альтернативная процедура получения результирующей оценки.

В целом наблюдается хорошая сходимость оценок параметров к истинным значениям. Условие приближенного "отслеживания" точки перегиба в форме 5 <  X * /120 было выполнено во всех случаях более чем с двукратным запасом.

АНАЛИЗ ПОГРЕШНОСТЕЙ ОЦЕНИВАНИЯ ПАРАМЕТРОВ КРИВОЙ ЛОГИСТИЧЕСКОГО

РОСТА

Общий вид оценки — а₀ = а ₀ + А а = а ₀(1 + г_а ) при А а и е_а — абсолютной и относительной погрешностях. В первом приближении (приближении дифференциала первого порядка) для 3-точечной схемы (7) абсолютная погрешность имеет вид:

Аа « X(KnZn + Kn+1Zn+1 + Kn+2Zn+2), где

K n =- ( t + 2 + 1/ 1 ) , a о - ¹

Kn+1 = a^+Y ( t / a 0 + 2 + a 0/ t ) , a 0 - 1

^K n + 2 =        ?( t / a 0 ^{+ 2 +} a 2 / t ) .

a ₀ - 1

Учитывая характер аддитивных случайных погрешностей, в частности их центрированность и независимость, можно сделать выводы:

• а)    оценка — несмещенная;

• б)    ее дисперсия равна

7 a = Дг _s 2 7 о2 ( K n + _K, + K 2 ).

(X *)

Здесь σ ₀² — дисперсия исходной помехи, приведенная к диапазону [–1, 1]. В случае равномерной помехи 7 02 = 1/ 3 . Выражение в круглых скобках является функцией t , и возможны постановка и решение задачи поиска минимума соответствующей функции. Как говорилось ранее, имеется нетривиальное решение t ® 1.7, слабо зависящее от a ₀ ( t » 1.73 при a ₀ = 2, t « 1.68 при a ₀ = 1.9, t » 1.61 при а 0 = 1.8). В частности, при a 0 = 2 минимальная дисперсия ошибки оценивания

7 2 « 4 ' ^242.268 ( 5 / X * )² « 323 ( ₅ / X * )².

В общем случае при произвольных истинных значениях параметров кривой оптимуму может соответствовать нецелое значение n , и потребуется выбрать ближайший к точке оптимума отсчет n .

Схожий вид (и аналогичные свойства) имеет дисперсия ошибки определения a 0 при 4-точечной схеме (8):

7 2 = Г-0^ ⁵ 2 7 02 ^( K n + K + 1 + K n + k + K n + k + 1 ), (13) ( X * )        ^{k 2}

где

Kn =-(t+2+1/1), a0 - 1

Kn+1 =       (t /a 0 + 2 + a 0/t ) , a0 - 1

Kn+k = -a°Y (t /a 0 k + 2 + a 0 k / t), a0 - 1

^K n + k + 1 =          "( t / ^a 0 k ^{+ 1 + 2 + a} 0 k ^{+ 1} / t ) .

a ₀ - 1

Правые множители формируют функцию 2 пе- ременных (t, k), и возможен поиск минимума указанной функции. Точка минимума при заданном a0 искалась приближенным методом спирального (координатного) спуска. Как говорилось ранее, координаты этой точки слабо зависят от a0. При эффективно реализованной ПЦР (т. е. при a0 ~ 2) точка оптимума лежит вблизи t = 4.7, k = 4. В этом случае минимальная дисперсия ошибки оценива-2 4 • 26.500^._v ния определяется как 72 ~---(5 / X ) ~

~ 35.3 ( 5 / X * ) 2 . Тем самым стандартное отклонение оценки (13) в случае 4-точечной оптимальной схемы будет приблизительно в 3 раза меньшим по сравнению с (12), т. е. аналогичной 3-точечной схемой.

Проведенное имитационное моделирование, включающее генерацию идеальной кривой логистического роста и аддитивной помехи с заданным законом распределения (100–250 различных реализаций), подтверждает указанные выше закономерности оценки а 0 . В частности, близкая к оптимальной 4-точечная схема при заданных условиях ( а 0 = 2.000; Х = 3000; Х 0 = 10; δ = 5) дает следующие характеристики оценки а 0 : математическое ожидание 1.99939, среднеквадратичное отклонение 0.01023 (в соответствии с расчетной формулой (13), среднеквадратичное отклонение в указанных условиях должно составить 0.009907). Некоторое расхождение может быть объяснено неидеально-стью характеристик датчика равномерной случайной величины. В частности, не в полной мере обеспечивается несмещенность случайной величины, имеются незначительные асимметрия и превышение коэффициента эксцесса.

При анализе ошибки оценивания Х*, связанной как с наличием аддитивной погрешности в базовых измерениях Xn и Xn+k, так и с погрешностью оценивания a0, следует учитывать, что погрешности могут не быть независимыми, если оценивание a0 и Х* базируется на одних и тех же измерениях (на отсчетах n и n + k). Представляет интерес решение задачи о выборе точек для оценивания Х*: что является более выгодным по точности — использование общих точек или различных? Решение этой задачи будет приведено далее.

В первом приближении приращение функции нескольких переменных можно вычислить на основе аналога дифференциала первого порядка: dX*л     X*лу   dX*

A X =---A a ₀ +---A X „ +-----A X_n+m при ис- d a 0    ⁰ d X n ⁿ a X n + m ^{n +} m    ^p

V*          at₀m - 1

пользовании оценки X =------0--------, ана- aim / Xn+m -1/Xn логичной (9). Здесь приращения AXn и AXn+m равны соответственно ζn и ζn+m. (Номера n и n + m могут не совпадать с аналогичными номерами отсчетов, по которым осуществлялось оценивание a0).

Задавая t * = ( B - 1) / a 0* , получим, m X * t * S X * = 1_ + t ._

" a m - 1 a ₀ , d X n a m - 1⁽     )

dX * что da 0

dX * и dX+m

a

m 0

a 0 ^m - 1

( 1 + t * I a m ) . В случае несовпадения отсче-

тов, по которым осуществлялось оценивание a 0 и

X *, все три слагаемых в A X будут независимы, и соответствующие дисперсии оценок сложатся:

σ_X ² *

( a 0¹

—

m ( x * ) 2 ( t * ) ²

σ

a ₀

+

+ a ₀ ² m (1 + t * I a m )² 5 ² о ₀ ² + (1 + t * )² 5 ² о ₀ ²

У этой функции имеется тривиальный асимптотический минимум t * ^ 0. Практически это означает, что наиболее точные измерения X выпол-

няются при максимальных номерах отсчетов n и n + m . Таким образом, для нескольких последних измерений требуется вычислить t ^*; в случае его малости дисперсия ошибки оценивания Х ^* будет

примерно равна σ_X ² *

a ₀ ^{2 m} + 1

( a m - 1)²

δ ² σ ₀² , т. е. лишь не-

значительно превзойдет дисперсию аддитивной помехи, равную δ ² σ ₀² .

Другим подходом является оценивание X ^* на основе тех же измерений, что и при вычислении оценки a 0 , т. е. t ^* = t , m = k для 4-точечной схемы (8). При этом для оценивания a 0 и X ^* (по (9)) использованы одни и те же отсчеты n , n + 1, n + k и n + k + 1 и

A X * «

”     (KZ + KZ+1 + K**+Z*+k+Kn+k+Z*+k+1), a ok -1

где

K* = at (t + 2 +1/1) - (1 +1), a0 - 1

Kn+1 =       7 (t 1 a 0 + 2 + a 0 / t) , a0 - 1

Kn+k =     °"7"(t / a0 + 2 + ak / t) + ak + t , a0 - 1

K * ₊ k + 1 = ^0 ^ 7 ( t / a 0 ^{k + 1} + 2 + a 0 ^{k + 1}/ 1 ). a ₀ - 1

Поскольку все четыре слагаемых являются независимыми, то их дисперсии складываются при вычислении дисперсии оценивания X . Наиболь-

шая по абсолютной величине ошибка оценивания X ^* определяется полуразмахом помехи δ , а также абсолютными значениями коэффициентов K i ^* . Если значение t находится достаточно близко к 4 (т. е. вблизи оптимума для вычисления а 0 ), то максимальная погрешность оценивания X теоретически может составить около 12 δ , т. е. огромную величину (хотя и вероятность этого ничтожно мала).

Вывод. Многократно более эффективной является следующая реализация алгоритма:

– на первом этапе при режимах, близких к оптимальным, производится оценивание параметра a 0 ;

– на втором этапе по набору измерений, достаточно близких к участку насыщения (т. е. по заключительным имеющимся отсчетам кривой логистического роста, соответствующим достаточно малым t ^*), производится, согласно (9), оценивание другого параметра X ^*. Эффективность подобного подхода при оценивании X ^* иллюстрируется далее.

Пусть, для примера, сгенерирована последовательность 40 отсчетов с параметрами a 0 = 1.910; X ^* = 3000; X 0 = 0.50 и добавлена равномерная центрированная помеха с δ = 10. Далее по (8) с k = 4 и n = 10–15 проведено оценивание a 0 . После этого выполнен расчет X ^* по тем же отсчетам. Получены следующие оценки: 3063, 2997, 2982, 3002, 3001, 3009 (стандартное отклонение о « 29.6). Для сравнения по измерениям n = 29–34 последовательность таких же оценок (9) для X ^* имеет вид: 2990, 3010, 2994, 3006, 3004, 3004 ( о » 7.8). Таким образом, оценивание X ^* по более поздним отсчетам является существенно более эффективным, исходя из величины среднеквадратичного отклонения ошибки оценивания. Аналогичная тенденция наблюдается и при иных параметрах a 0 , X ^*, X 0 и диапазоне помехи.

Заключительным этапом является оценивание параметра В и на его основе величины порогового цикла n ^* как точки перегиба кривой логистического роста. Используется формула (10) и строятся выборки значений F = ln(2 B - 1) = ln( X * / X n - 1) + + n ln((i₀). Тогда погрешность оценивания величины F в приближении первого дифференциала бу

,    dF ,     dF , ,   dF       „ дет AF =---Aan +---AX +---AX„. Полагаем, da 0   0 dX *       dXn    n что предшествующие параметры были оценены ранее в оптимальных условиях и, следовательно, по различным отсчетам. Тем самым соответствующие погрешности оценивания были независимы, и дисперсии могут складываться.

Частные производные равны соответственно dF            dF     1

= n I an,           =               и da 0      0      dX * X * - Xnd

1      ( - X *)

X */ X n - 1 " X T

X ^*

X n ( X * - X n )

. Полагая, что

измерение X n = X * / (1 + t '), где t' не совпадает ни со значениями t (при условиях оптимального вычисления a 0 ), ни со значениями t ^* (при оптимальном вычислении X ) получим следующее.

• а)    Дисперсии а 0 и X при оптимальных режимах оценивания равны соответственно 106 5 2 с ₀ 2 / ( X * ) 2

и δ2σ02 (т. к. дисперсия ошибки оценивания X * в оптимальных условиях оценивания лишь незначительно превосходит дисперсию аддитивной помехи любого из измерений).

• б)    В приведенных выше обозначениях

d F _ 11 + 1' d F 1XC = X * Ч⁷" ’ d Xn - ln( t *)) /ln( a ₀).

(1 + 1 ') 2

X ^* t '

и n = (ln( B - 1) -

• в)    Тогда дисперсия ошибки оценивания F при-

• 5 2c02 (1 +1 ')4 (1 +1 ')2 1 _,n2 мерно равна —+      + 106— .

( X * ) L t           t             ^a 02 J

В принципе возможен поиск минимума дисперсии по параметру t', который, безусловно, зависит от истинного значения В. Необходимое условие экстремума при этих данных сведется к поиску положительного решения трансцендентного урав- нения a02 ln2 (a0)

ln( t ') - 4/ 1 ¹² -

6/ 1 ' + 4 1 ' + 2 1 ¹² =

Наиболее удобной представляется робастная модификация Фабиана—Цыпкина. Основанием для использования указанного алгоритма служит модель сигнала (выборка оценок, представляющая собой постоянную величину — истинное значение с аддитивной помехой с априорно неизвестным законом распределения).

Общие принципы организации алгоритма оценивания достаточно детально рассмотрены в работах [13, 14]. Выполняется рекурсивное построение оценок по правилу:

c n + 1 = c n ^{- в} / ⁿ • ^ ⁽ c n ^- x n + 1 ) . ⁽¹⁵⁾

- 1, для z <-А ,

При этом у(z ) = <  0,

I z <^A ,

. 1, z >A ;

xn+1=c*+ξn+1 — измерение; ξn+1 — помеха; сn, cn+1 — оценки величины с* на n-м и n+1-м шагах оценивания; в — параметр алгоритма; 2А — величина зоны нечувствительности. В предельном случае (15) при А = 0 получается сигнатурный алгоритм Я.З. Цыпкина, т. к. Т(z) = sign(z). Начальное приближение с1 оценок a0, X* и X0 может совпадать с первой из полученных оценок. При оценивании a0 в качестве первого приближения можно выбрать и априорную оценку 1.90, соответствующую средней эффективности ПЦР.

Степень близости оценки к истинному значению можно определить в соответствии с [13, 14] на основе анализа знака "поправок", т. е. при на- личии немонотонности последовательности оценок. В противном случае при монотонном увеличении (уменьшении) оценок достаточно вероятно расхождение оценки и истинного значения параметра. При оценивании X* и X0 априорная информации о возможном значении этих параметров отсутствует, и в качестве первого приближения следует брать первую оценку величины.

Параметр β в (15) соизмерим с дисперсией соответствующей оценки: при оценивании X ^* сопоставим с величиной δ (т. е. 10–15 квантов), при оценивании а 0 дисперсия оценки близка к 6 δ / X ^* (т. е. около 0.03). Соответствующий выбор β требует использования значений 0.05–0.10. Наконец, при оценивании величины F = ln( B – 1) стандартное отклонение примерно равно 20 δ / X ^*, т. е. около 0.1. Тем самым следует выбрать β порядка 0.2. Выбранная величина зоны нечувствительности 2 А должна быть сопоставима с требуемой точностью определения параметра. С практической точки зрения достаточным является оценивание а 0 с точностью до 0.01, X ^* с точностью до 1 или даже нескольких квантов, точность при оценивании F определяет с масштабным множителем 1/ ln( а ₀) ~ 1.4^1.7 погрешность нахождения положения порогового цикла n ^*.

Выборки измерений параметров и оценок, полученных по алгоритму (15)

β	∆	Параметр	Измерения / оценки*						Итоговая оценка
0.03	0.001	а 0	1.918	1.896	1.918	1.906	1.917	1.927	1.917
			1.918	1.888	1.903	1.903	1.911	1.917
10	0.5	Х *	3492	3511	3494	3506	3504	3504	3504.8
			3492	3502	3497	3500.3	3502.8	3504.8
0.5	0.01	F	12.029	12.031	12.042	12.045	12.038	12.051	12.05
			12.03	12.03	12.08	12.05	12.03	12.05

*

Измерения в верхней строке, оценки — в нижней.

Представляется достаточным нахождение n ^* с точностью до 0.2–0.3 цикла (отсчета). Тогда получаем результирующие оценки параметров на базе процедуры стохастической аппроксимации (в таблице). По правилу знаков "поправок", эти оценки близки к истинному значению. Исходные оценки, приведенные в таблице, получены при условиях, близких к оптимальным. Результирующие оценки: а 0 = 1.917, X ^* = 3504.8, F = 12.05, из чего следует, что B ≈ 171100, X 0 ≈ 0.0205 и n ^* ≈ 18.52. Они весьма близки к исходным данным, приведенным в разделе "Имитационное моделирование…".

ЗАКЛЮЧЕНИЕ

В работе исследованы различные алгоритмы оценивания параметров кривой логистического роста. Объединяющим принципом является переход к построению оценок в форме постоянного сигнала (тренда нулевого порядка) с аддитивной случайной помехой. Были проанализированы возможные алгоритмы построения подобных оценок, описаны законы формирования случайной погрешности оценки с доказательством центрированности соответствующих плотностей распределения вероятностей, а также решены задачи оптимизации выбора базовых отсчетов по критерию минимизации дисперсии ошибок оценивания. Учет влияния систематической составляющей сигнала планируется осуществить в ч. 2 статьи.

Данная работа выполнялась при финансовой поддержке в рамках программ и проектов: Аналитической ведомственной целевой программы "Развитие научного потенциала высшей школы" — проект "Исследования и диагностика клеточных структур: новые методические подходы и инстру- ментальные решения на основе сканирующей зондовой микроскопии и микрочиповых технологий" (№ 4247); Программы фундаментальных исследований Президиума РАН № 20 "Создание и совершенствование методов химического анализа и исследования структуры веществ и материалов" — проект "Микрочиповые аналитические системы для метода молекулярных колоний"; Программы фундаментальных исследований Президиума РАН на 2009 г. № 27 "Основы фундаментальных исследований нанотехнологий и наноматериалов".