Методы оценивания параметров кривой логистического роста. Ч. 2. Оценивание и компенсация систематической погрешности измерения. Сопоставление двух различных форм математической модели логистического роста

Одной из принятых форм информативного сигнала в приборах, реализующих полимеразную цепную реакцию в реальном масштабе времени, является кривая логистического роста

X = X *

n 1 + ( B - 1) a 0 n

.

Здесь Х n — величина сигнала на n -м шаге измерения ( n = 0, 1,…, N при N = 30÷40).

Характеристика зависимости (1), интерпретация роли информативных параметров a 0 , Х ^* и Х 0 , обоснование алгоритмов их оценивания, а также оптимизация выбора отсчетов сигнала для повышения эффективности оценок были даны в первой части статьи [1].

В ч. 2 данной работы описаны алгоритмы выявления и компенсации систематических составляющих сигнала. Кроме того, проанализировано другое достаточно распространенное описание процесса логистического роста (2), включающее степенную зависимость

X = A + A ¹ - A ² ,            (2)

n 2                            ,

• 1    + ( n / n ) p

и установлена связь между параметрами обеих моделей.

КОМПЕНСАЦИЯ НАЧАЛЬНОГО ДРЕЙФА СИГНАЛА ЛОГИСТИЧЕСКОГО РОСТА

Проведение измерений может осуществляться в условиях, когда имеется дрейф базовой линии, интерпретируемый как систематическая погрешность измерения. При этом малому информативному сигналу на начальных отсчетах n , когда количество ДНК еще мало, соответствует значительный фоновый сигнал. Очевидно, что он требует оценивания или/и компенсации.

Однако предварительный анализ кривой (1) позволяет осуществить две простые экспресс-оценки сигнала насыщения Х ^*.

• а)    В [1] были сформулированы критерии поиска порогового цикла (точки кривой с наименьшей кривизной). В этой точке информативная составляющая сигнала должна быть равна 0.5 Х ^*.

• б)    Размах сигнала даже с учетом возможности недостижения уровня насыщения должен примерно соответствовать Х ^*.

Таким образом, приближенные экспресс-оценки Х ^* могут быть выполнены на основе таких простых рассуждений.

Рассматриваются алгоритмы компенсации фонового сигнала, исходя из предположения, что этот сигнал адекватно аппроксимируется полиномом либо нулевого, либо первого порядка. В этом случае возможны два подхода: аппроксимация или/и компенсация соответствующего тренда ма- лого порядка по Кендаллу—Стьюарту [2], либо оценивание параметров, например, по МНК с последующей экстраполяцией на все отсчеты и компенсацией.

Определение величины фонового сигнала Z n = = Z = const( n ) базируется на гипотезе, что Z аддитивно суммируется со всеми информативными сигналами, т. е. вместо X n измеряется X n + Z . Экспресс-оценивание параметров Х ^* и Х 0 кривой (1), а также Z возможно на основе следующих предположений.

• а)    По критерию смены знака второй разности можно определить примерное положение порогового цикла    n * .   При указанном    n = n *

X . = 0.5 X * + Z . n

• б)    Полагая в первом приближении а 0 = 1.90, можно оценить B = X * / X ₀ + 1 = a 0 .

• в)    На начальных отсчетах n , когда B / a 0 >>  1, соответствующий оцениваемый сигнал близок к Z ; на конечных отсчетах, близких к стадии насыщения, если она достигается, при B / a 0 <<  1 величина сигнала должна быть близка к X * + Z . Таким образом, можно приближенно оценить величину Z и произвести ее компенсацию.

После компенсации Z можно исследовать информативный сигнал в тех интервалах отсчетов, когда он достаточно слабо меняется по величине, т. е. при n <<  n * (информативная составляющая мала по величине) или/и n >>  n * (информативная составляющая практически не меняется из-за достижения насыщения). По нескольким отсчетам строится линейная аппроксимация, оценивается величина параметра положения сигнала и значимость наличия тренда первого порядка (например, по критерию Фишера или аналогичному [3, 4]). Далее линейный тренд экстраполируется на весь диапазон отсчетов n и компенсируется (вычитается) эта составляющая систематической погрешности.

Вышеописанный алгоритм проиллюстрируем простым примером: генерируем кривую (1) с параметрами а 0 = 1.950, Х ^* = 2000, Х 0 = 1, n = 0, 1,…, 30. Внесем аддитивную случайную центрированную помеху, сгенерированную по равномерному закону в диапазоне [–10; +10], и постоянную систематическую погрешность Z = +200. Некоторые значимые отсчеты суммарного сигнала приведены в табл. 1.

Расчет сигнала второй разности по отсчетам 10, 11, 12 дает (–15.9); по отсчетам 11, 12, 13 — (+22.3). Можно убедиться, что по крайней мере в 2 последующих и предшествующих отсчетах знак второй разности сохраняется. Тогда на интервале 11–12 отсчетов наблюдается перегиб. Более точная его локализация с помощью линейной интерполяции по величине второй разности дает n ^* = = 11.41 и, следовательно, X n * = 1205.1.

Экспресс-оценка В = 1.90¹¹ ' ⁴¹ + 1 ~ 1516. Отсчетам n = 0.. .3 соответствуют t >  221 и, следовательно, сигналы, близкие по величине к Z . Отсчетам n >  24 соответствуют t <  310^-4 и сигнал, практически равный Х ^* + Z . С помощью МНК для n = = 0…3 и n = 24…30 строим линейные аппроксимации:

• а)    для первого участка X n = 191.08 + 2.90 ■ n ;

• б)    для второго участка X n = 2208.58 -- 1.24 ■ ( n - 24) либо с соизмеримой точностью X n = 2204.90 = const ( n ).

Cредние значения сигнала на первом и втором участках рассматриваются как Z и X * + Z . (При этом 0.5 Х ^* + Z примерно равен 1205.1). Тогда Z « 191.08 + 2.90 - 1.5 = 195.4 и X * + Z « 2204.9. Следовательно, X « 2009.5 (значение сигнала при n = n * должно быть примерно равно 0.5 ■ 2009.5 + + 195.4 = 1200.2).

Табл. 1. Отсчеты сигнала на участках малого изменения информативной составляющей

n	X n	n	X n	n	X n
0	191.2	7	295.7	24	2208.6
1	192.0	8	393.4	25	2206.6
2	200.5	9	547.8	26	2208.4
3	198.1	10	764.6	27	2206.2
4	211.5	11	1072.4	28	2199.0
5	222.2	12	1396.1	29	2202.1
6	254.3	13	1697.5	30	2203.2

Оценочное значение X 0 = X * / B ® ® 2009.5/1516 = 1.33. Тогда на начальных отсчетах логистический рост практически неограничен, носит экспоненциальный характер и осуществляется примерно по закону X ₀ • а 0 , т. е. при n = 0, 1, 2, 3 получим величины 1.33, 2.53, 4.80 и 9.12 (линейная аппроксимация соответствующего фрагмента сигнала позволяет получить оценку параметра положения, равную 2.56). Таким образом, наклон линейной аппроксимации практически полностью объясняется логистическим ростом, и, следовательно, аддитивной систематической погрешности типа линейного тренда первого порядка не имеется .

СРАВНЕНИЕ ДВУХ МОДЕЛЕЙ КРИВЫХ ЛОГИСТИЧЕСКОГО РОСТА

Кривая логистического роста описывается двумя зависимостями (1) и (2), отличающимися различным числом информативных параметров и типом используемых функций. В (1) входит показательная функция, в (2) — степеннáя. Существенным представляется вопрос о связи параметров моделей: ( X ^*, X ₀, a ₀) и ( A ₁, A ₂, n ^*, p ) . Первые два параметра в обеих моделях имеют один и тот же смысл: начальный сигнал X ₀ = А 1 и сигнал насыщения X * = А ₂. Два оставшихся параметра модели (2) можно связать с параметрами модели (1) на основе сопоставления временнóго положения и динамики информативного сигнала в области наиболее линейной фазы сигнала, т. е. на цикле n ₀ = ln( X * / X ₀ - 1) / ln( а ₀). Имеем n ₀ >>  1 при достаточно большом соотношении Х ^*/ Х 0 . Приравняв временнóе положение порогового цикла на основе моделей (1) и (2), а также d X_n /d n — скорость роста информативного сигнала в указанной временнóй области, получим соотношения

^{( n} * / ⁿ 0 ) ^p = ⁽ Р ^{- 1)/(} Р + 1)

Однако, выбрав в качестве критерия минимизацию среднеквадратичного отклонения обеих моделей на интервале отсчетов n = [0; N ], получим, что оптимальные оценки параметров А 1 , А 2 , n ^* и p расходятся с названными выше. Это связано, в частности, с тем, что скорости роста степеннóй и показательной функций различны, и в областях стыковки участков кривой "начальный участок"— "экспоненциальный рост" и "экспоненциальный рост"—"участок насыщения" имеются существенные расхождения обеих кривых.

Имитационное моделирование свидетельствует, что оптимальные значения n ₀ ~ n * , а остальные оптимальные значения имеют некоторые расхождения с приближенными оценками:

A 1 = X 0 ; A 2 = X * ; р = ⁿ 0 lⁿ⁽ a 0 ). ⁽³⁾

Задачу оптимизации предлагается решить следующим образом. Указанные три значения параметров (3) рассматриваются как первое итерационное приближение. Необходимые поправки для второго итерационного приближения определим в соответствии с алгоритмом:

а) выпишем функционал качества

Ф ( A 1 , A 2 , Р ) =

N

= 1

n =0

X ^*

V 1 + ( X * / X 0 - 1) • а 0 -

(

A 2 + V

A 1 ^- A 2 )

1 + ( n / n *) Р j_j

; (4)

и

X * ln( а ₀)/4 =

( X* - X ₀)( p ² - 1) 4 pn ^*

• б)    вычисляются частные производные первого по-

• дф дф дф

рядка ;    ; при значениях параметров (3);

д A 1 д A ₂ д p

• в)    после необходимых итерационных приращений A A 1 , A A ₂, A p мы должны получить стационарную точку функционала Ф , в которой все частные производные первого порядка должны стать равными нулю (необходимое условие экстремума функции нескольких переменных);

• г)    приращения частных производных первого порядка в приближении второго дифференциала функции нескольких переменных равны:

дФ д ² Ф . .

A -    . Л А 1 +

д ² Ф

Т. к.

X * / X ₀ >>  1 ^ n * >>  1 ^ p >>  1 ^ p ~ n * ln( а ₀),

*     /Р - 1     L 2    )

ⁿ = ⁿ 0 ^p ----7 ~ ⁿ 0 ¹-- 7---- 77 Г ⁿ 0. Т. ^е. харак^-

V Р +1 V Р(Р - 1) j терный временнóй масштаб n* из (2) практически совпадает с величиной порогового цикла n*. Тем самым в первом приближении возможно связать параметры обеих моделей кривых логистического роста.

дА1 дА12

_к дФ   д ² Ф

A--«---- дА2 дА1дА2

д А 1 д А

AA

A A . +---- A A ₂

1   22

д ² Ф

+-- дА1дp д2Ф

A p ;

+-- дA 2дp

A p ;

дФ д ² Ф      д ² Ф      д ² Ф

A ®-----A A . +-----A A ₂ +---A p .

д p д А 1 д p      д p д А 2        д p ²

При этом производные первого порядка выражаются, как

V;

V n

1 + Vn ’

—=— ;y ( x 1 — x 2 )■ d A₁     ^ ^{( n    n} ’

— = —2У (X1 — X2) dA2     ^( n    n ’ f^ _ 2(A — A )у ( xi — x2) Vnln(n / n ) dp       1      ^( n n) (1 + Vn)2

.

Здесь и далее введены обозначения X_n ¹

и

X_n ² — отсчеты кривых логистического роста в соответствии с моделями (1) и (2), V n = ( n / n * ) p .

Производные второго порядка определяются выражениями:

ф2У

8 A ;   ^

(1 + V n )²;

^ф 2! J-;

a A 1 a a 2     ^ (1 + V n )²

а ² Ф d A ₁ d p

= 2( A 2 — A 1 ) E Vn™ +

_{1      2} V_n ln( n / n ^*)

^{+ 2} ^ ⁽ X n ^— X n ) (1 + V ) 2 ’

^Ф = 2( A — a ^

d a d p                 (i + v n )³

—

_{— 2}V₍ X 1 _— X 2 ) ^V n ln⁽ n / n ‘) .

^( n n) (1 ₊ v ) 2 ;

дФ_ ₂₍ A _— A ₎₂y V n ²ln²( n / n * ) d p ^{2    ( 2}       ^    (1 + V n ) 4

—

-А (X 1 -X2) Vn (¹ — Vn )ln²( n / n *) ²⁽ A 2 A 1 ) ^ ⁽ X n X n )      (1 + v ) 3

.

Таким образом, на основе линейной системы уравнений (5) вычисляются необходимые приращения параметров А А ₁, А А ₂ и А p и второе итерационное приближение решения задачи минимизации функционала качества (4).

ПРИМЕР РАСЧЕТА ОПТИМАЛЬНО СОГЛАСОВАННЫХ ПО ПАРАМЕТРАМ

МОДЕЛЕЙ (1) И (2)

Рассмотрим кривую (1) с параметрами Х* = = 2000, Х0 = 0.2, а0 = 1.94. Первое итерационное приближение параметров степеннóй модели (2): А1 = 0.2; А2 = 2000; n * = 13.898; p = 9.210 (n * вычислен [1], как ln( X */ X0 — 1) / ln( a 0) = = ln(9999)/ln(1.94)). Дисперсию расхождения моделей можно оценить, как Ф(А1, А2, p) / (N +1 — 3), где Ф определен согласно (4), поскольку выборка содержит (N + 1) отсчет и 3 оцениваемых параметра. Вычисление частных производных и решение системы (5) для определения приращений параметров позволяет получить новое итерационное приближение: А1= 0.2 + 17.001 = 17.201; А2= 2000 + + 17.369 = 2017.369; р = 9.210 + 0.043 = 9.253. (Построение 10 итераций в соответствии с алгоритмом, встроенным в пакет ORIGIN 6.1, позволяет получить весьма близкие оценки: А1 = 17.198, А2 = = 2017.290, р = 9.256). Среднеквадратичное отклонение моделей при первой итерации значений параметров равно 25.06; при втором (уточненном) наборе параметров — 17.13. Взяв модель (1) с X* = = 3000; X0 = 0.05; a0 = 1.95, т. е. условия более позднего достижения порогового цикла (n* = = 16.474) и более эффективной ПЦР, в качестве оптимальных параметров по описанной выше методике получим: А1 = 16.691; А2 = 3028.084; р = = 10.945. Реализация итерационной процедуры по алгоритму ORIGIN дает весьма близкие оценки А1 = 16.601; А2 = 3028.149; р = 10.941. Тем самым подтверждается высокая точность решений задачи оптимизации "пересчета" параметров модели на основе итерационного приближения первого дифференциала и матрицы Гессе (т. е. системы (5)).

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ВЫПОЛНЕНИЯ ЦИКЛА АЛГОРИТМОВ ОБРАБОТКИ КРИВЫХ ЛОГИСТИЧЕСКОГО РОСТА

В качестве модельного сигнала генерируем последовательность отсчетов n = 0,…, 34 при заданных параметрах: Х ^* = 3200, Х 0 = 0.2, а 0 = 1.92. Далее аддитивно добавляем сгенерированную равномерно распределенную центрированную случайную величину в диапазоне [–16; +16] (оговоренное ранее условие Х / 5 >  120 выполнено). В качестве систематической погрешности задается линейный тренд первого порядка 250 + 2.0 • n . График сгенерированной зашумленной кривой и ее значимых фрагментов представлен далее.

На рис. 1 приведена форма кривой логистического роста с наложенными систематической и случайной погрешностями измерения. На графике схематически выделены участки: 1 — фаза начального роста, соответствующая малому количеству ДНК; 2 — наиболее линейный участок роста в области порогового цикла (точки перегиба); 3 — участок насыщения.

Далее проиллюстрированы основные стадии обработки указанного информативного сигнала. Заметим, что идеальной кривой логистического роста (1) соответствуют В = 3200 / 0.2 = 16000 и n ^* = ln(16000 – 1) / ln(1.92) = 14.840.

3500-1

3000 -      1

500-

Отсчеты

Рис. 1. Схематическое представление информативного сигнала в соответствии с моделью логистического роста.

Пояснения см. в тексте

Табл. 2. Величина сигнала на этапе насыщения логистической кривой

n	X n	n	X n	n	X n
23	3440.4	27	3456.1	31	3458.9
24	3438.3	28	3457.0	32	3451.8
25	344.1	29	3464.7	33	3471.4
26	3455.0	30	3447.5	34	3467.2

Табл. 3. Величина сигнала на начальном этапе кривой логистического роста

n	X n	n	X n	n	X n
0	195.6	3	197.7	6	214.8
1	193.3	4	217.2	—	—
2	205.9	5	229.6	—	—

Первый этап обработки предполагает выявление систематической погрешности, ее компенсацию и грубую оценку основных параметров кривой логистического роста.

Анализируем динамику второй разности исходного сигнала: при n = 12÷14 эти разности положительны (при n = 14 равна +86.07), далее при n = 15÷17 происходит смена знака (при n = 15 величина второй разности –17.08). Таким образом, на интервале 14–15 отсчетов находится точка перегиба (пороговый цикл). Методом линейной интерполяции определяется точка перехода второй разности через ноль: n ^* = 14.83 и Х n * = 1834.4.

В предположении формы графика систематической погрешности, как линейной, тренд первого порядка Xn* примерно соответствует 0.5Х* + α0 + + α1n*. Эффективность ПЦР априорно полагаем средней, т. е. a0 = 1.90 . Т. к. a08 = 1.98 ≈ 170 , то отклонение от порогового цикла на +8 тактов соответствует стадии насыщения сигнала (информативная составляющая практически совпадает с Х*); участок, предшествующий пороговому циклу на 8 тактов и более, — начальный участок экспоненциального роста (полезная составляющая сигнала близка к X0 ⋅ a0n ). На основе временнóго положения порогового цикла получаем примерное отношение Х* / Х0= = 1+1.914.83= 13610.

В табл. 2 и 3 представлены значения фрагментов сгенерированного информативного сигнала — на этапе насыщения (отсчеты 23–34) и на начальном этапе (отсчеты 0–6).

На основе МНК данные таблицы аппроксимированы трендом первого порядка 3394 + 2.13^. n , что иллюстрируется на рис. 2. Таким образом, сумма Х ^* + α 0 ≈ 3394 при α 1 ≈ 2.13.

Аппроксимация X_n = f ( n ) данных табл. 3 по МНК дает зависимость 192.6 + 5.04 ⋅ n . Можно сделать следующие выводы:

• а)    систематическая погрешность содержит постоянное смещение ( α 0 ≈ 190);

• б)    параметр положения линейного тренда ( α 1 ≈ ≈ 2.1);

• в)    большие значения параметра α 1 ≈ 5.0 связаны с информативным слагаемым (экспоненциальным ростом);

• г)    разность между свободными членами на обоих участках (3394 – 190 = 3204) примерно соответствует величине сигнала насыщения Х ^*.

Для проверки проанализируем предполагаемую точку перегиба (измерение на пороговом цикле): компенсировав из сигнала 1834.4 и систематическую составляющую, равную α0 + α1 ⋅ n* ≈ ≈ 190 + 2.1 ⋅14.83 ≈ 221 , должны получить около 1613, что примерно соответствует требуемому уровню 0.5Х* = 1602. Таким образом, в первом приближении можно полагать сигнал насыщения 3204. Следовательно, оценка начального информативного сигнала Х0 составит 3204 / 13610 ≈ ≈ 0.235. Информативная составляющая сигнала на начальных отсчетах приближенно соответствует X0 ⋅ a0n ≈ 0.235 ⋅1.9n . При аппроксимации этой зависимости линейным трендом по МНК получим 1.57 +1.63 ⋅ n Разность вычисленных параметров положения 5.0 – 2.1 = 2.9 в значительной степени объясняется "наложенным" информативным экспоненциальным ростом. Кроме того, истинное значение параметра a0 может превосходить априорно заданный средний уровень 1.90, а наличие случайной помехи большого (по сравнению с изменением сигнала на начальных отсчетах) диапазона также может исказить оцененную величину параметра положения систематической погрешности. В целом можно полагать, что в первом приближении систематическую погрешность можно аппроксимировать зависимостью 190 + 2.1n. Далее эта систематическая погрешность компенсируется.

После компенсации систематической составляющей сигнала осуществляется более точное оценивание информативных составляющих сигнала — а 0 , Х ^* и Х 0 по методикам, описанным выше. Также следует заметить, что проведенная компенсация линейного тренда первого порядка не повлияла на оценку положения порогового цикла (точки перегиба), т. к. последний определяется вторым разностным сигналом, а вторая разность от линейного тренда первого порядка есть ноль.

Ранее [1] были найдены условия оптимального оценивания параметра а 0 (4-точечная схема, включающая измерения на отсчетах n , n + 1, n + 4 и n + 5, т. к. в большинстве случаев оптимальным является k = 4). Было определено, что оптимальный отсчет n должен соответствовать t = 4.5÷5, т. е. примерно на 3 отсчета предшествовать пороговому циклу. Однако, поскольку предварительно осуществлялась компенсация систематической составляющей, целесообразно использовать отсчеты с большими величинами информативного сигнала, т. к. эффект неточной компенсации систематической составляющей информативного сигнала будет в этом случае менее значим.

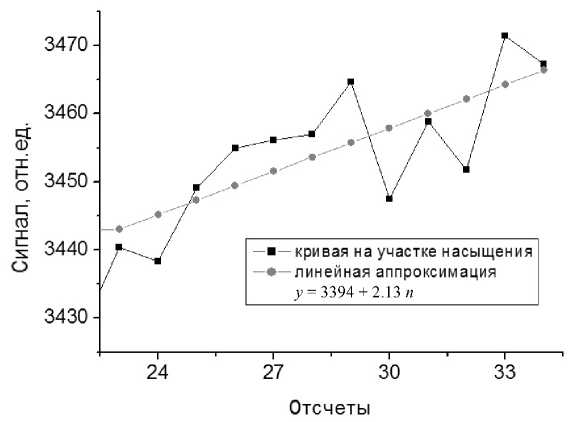
Рис. 2. Выделение систематической погрешности как линейного тренда первого порядка на стадии насыщения

Табл. 4. Величины отсчетов сигнала после компенсации систематической составляющей

n	X n	n	X n	n	X n	n	X n
27	3209	29	3214	31	3204	33	3212
28	3208	30	3195	32	3195	34	3206

Табл. 5. Выборка оценок параметра F

F	n
	11	10	12	13	14	15
	9.654	9.589	9.681	9.643	9.656	9.702

Для иллюстрации выберем четыре 4-точечные схемы, соответствующие n = 12÷15. Расчет параметра a 0 даст следующие оценки: 1.944; 1.948; 1.894 и 1.838. Выбрав медиану этих 4 измерений, получим (1.944 + 1.894) / 2 ® 1.919.

Для сравнения, использование близких 4-точечных схем по отсчетам (13, 14, 16, 17), (13, 14, 18, 19) и (12, 13, 18, 19) дает достаточно близкие оценки: 1.895, 1.889 и 1.922 соответственно.

После оценивания а 0 осуществляется расчет оценок Х ^*. Как говорилось ранее, более эффективные оценки будут при использовании наибольших по величине измерений (близких к стадии насыщения). Измерения на заключительных отсчетах кривой (от 27 до 34-го) после компенсации аппроксимированной систематической погрешности и округленные до целочисленных значений представлены в табл. 4.

Использовав пары значений сигнала на отсчетах 27–31, 28–32, 29–33, 30–34, применили формулу расчета Х ^* из [1] при k = 4 и оцененное значение параметра а 0 = 1.919. Тогда оценки Х ^* практически совпадают с вышеуказанными измерениями, поскольку стадия насыщения практически достигнута: 3203.6; 3194.0; 3211.8 и 3206.9. В этих условиях дисперсия ошибки оценивания должна лишь незначительно превышать дисперсию исходной помехи (стандартное отклонение исходной равномерной помехи с полуразмахом δ = 16 есть 9.24). В соответствии с медианной оценкой получим, что Х « (3206.9 + 3203.6) / 2 = 3205.3.

Заключительный оцениваемый параметр F связан с отношением Х* / Х0. В соответствии с методикой [1] наиболее эффективное оценивание этого параметра осуществляется при отсчетах, примерно соответствующих t = 12÷15 (требуется решение трансцендентного уравнения). Т. к. t = 1 — точка перегиба (пороговый цикл), a0 близко к 2.0, то требуется выбрать отсчет, предшествующий пороговому циклу на An: An = ln(t) / ln(a0) = 4 ^ 5. Однако по соображениям, высказанным ранее, следу- ет несколько сместить отсчеты в сторону больших измерений. В табл. 5 приведены оценки параметра F на основе измерений n = 10÷15. По медианному алгоритму получено F = 9.655. Следовательно, В = = 15600 и Х0 = 0.205. Пороговый цикл вычисляется, как F/ln(a0) = 14.816. Поскольку оценочные значения параметров получились весьма близкими к истинным, то и достаточно устойчивая оценка положения порогового цикла оказалась весьма близкой к истинному значению.

В заключительной стадии обработки информативного сигнала можно осуществить сопоставление найденных параметров модели (1) с параметрами альтернативной модели (2). Первая итерация параметров: n 0 = n * = 14.816, A 1 = X 0 = 0.205, A ₂ = X * = 3205.3 и p = n ₀/ln( a 0 ) = 9.655. Применив алгоритм уточнения параметров, основанный на решении системы (5), получим необходимые приращения параметров и новые итерационные значения: A A 1 = 25.995 ^ A = 26.200, A A = 21.71 ^ A ₂ = 3227.01 и A p = 0.083 ^ A = 9.738. Среднеквадратичное отклонение двух кривых составит: при первой итерации параметров 36.17 отсчетов, при второй итерации — 25.88. На рис. 3 иллюстрируется совпадение кривых, построенных на основе различных моделей логистического роста. Взяты значимые фрагменты, поскольку на начальной стадии и на стадии насыщения обе модели обеспечивают близкие значения (соответственно к величинам Х 0 и Х ^*). Наиболее "расходящейся" стадией являются участки с наибольшей кривизной сигнала, т. е. на границах областей 1—2 и 2— 3 (см. рис. 2). Более детализированные укрупненные фрагменты представлены на рис. 4 (а и б).

Разумеется, проиллюстрирована лишь общая схема оценивания информативных параметров кривых логистического роста. В частности, возможно формирование как более представительной статистики оценок параметров (за счет варьирования выбора n и k вблизи оптимальных условий),

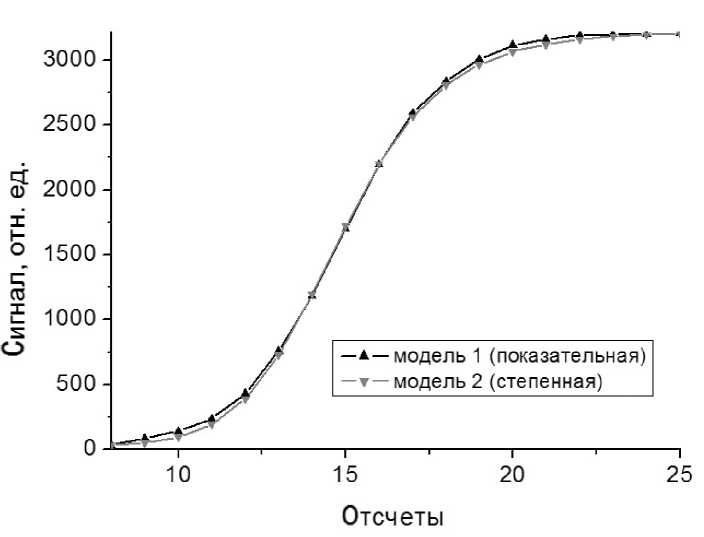
Рис. 3. Сравнение форм кривых логистического роста, сформированных на основе различных моделей

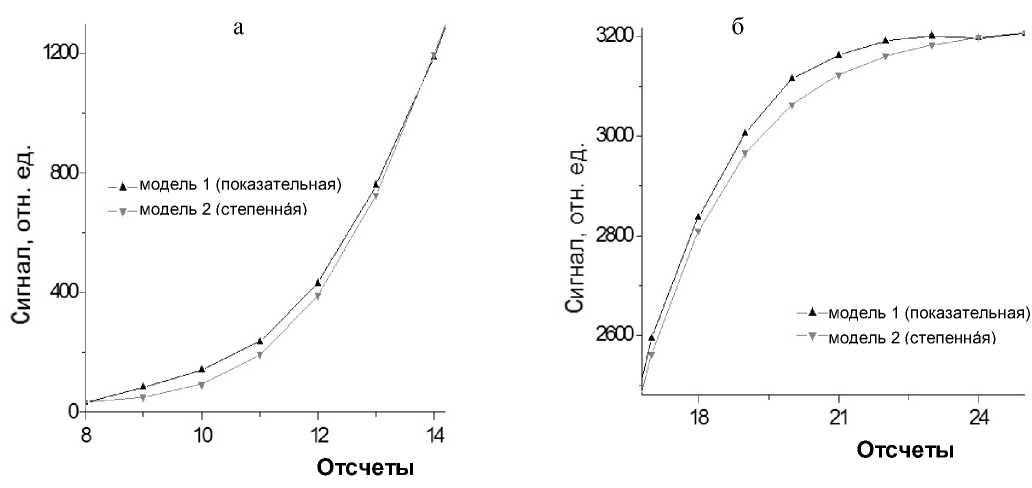
Рис. 4. Различие кривых логистического роста, сформированных в соответствии с различными математическими моделями.

а — фрагмент в области перехода режимов 1—2; б — фрагмент в области перехода режимов 2—3

так и другие принципы отбора результирующей оценки из выборки. Например, в [1] для формирования результирующей оценки параметров рассмотрен алгоритм стохастической аппроксимации.

Другая предложенная оценка в форме медианы по четному числу измерений алгоритмически является усеченным средним, т. е. учитывает различие оценок, обладает необходимой робастностью (ус- тойчивостью к выбросам) и мало отличается по своим характеристикам от оценки на основе алгоритма стохастической аппроксимации.

ЗАКЛЮЧЕНИЕ

Показаны возможности эффективной компенсации систематической составляющей сигнала, а также надежного оценивания параметров моделей логистического роста. Кроме того, детально описана процедура сопоставления двух наиболее распространенных форм (1) и (2) решения логистического уравнения, использующих показательные и степенн ы е функции. Рассмотренные в ч. 1 и 2 алгоритмы позволяют осуществить обработку соответствующих кривых (информативных сигналов) и в конечном счете способствуют получению необходимой аналитической информации при реализации ПЦР-РВ.

Данная работа выполнялась при финансовой поддержке в рамках программ и проектов: Аналитической ведомственной целевой программы "Развитие научного потенциала высшей школы" — проект "Исследования и диагностика клеточных структур: новые методические подходы и инструментальные решения на основе сканирующей зондовой микроскопии и микрочиповых технологий" (№ 4247); Программы фундаментальных исследований Президиума РАН № 20 "Создание и совер- шенствование методов химического анализа и исследования структуры веществ и материалов" — проект "Микрочиповые аналитические системы для метода молекулярных колоний"; Программы фундаментальных исследований Президиума РАН на 2009 г. № 27 "Основы фундаментальных исследований нанотехнологий и наноматериалов".