Методы оценивания спектральных и временных параметров сигналов на основе теории сплайн-алгебраического гармонического анализа

Агиевич Сергей Николаевич; Agievich S.N.

Научные статьи \ Прикладные науки. Медицина. Технология \ Инженерное дело. Техника в целом \ Общее машиностроение. Ядерная технология. Электротехника. Технология машиностроения \ Электротехника

Методы оценивания спектральных и временных параметров сигналов на основе теории сплайн-алгебраического гармонического анализа

Автор: Агиевич Сергей Николаевич

Журнал: Научное приборостроение @nauchnoe-priborostroenie

Рубрика: Математические модели физико-технических систем

Статья в выпуске: 2 т.22, 2012 года.

Бесплатный доступ

Предлагаются разработанные методы и реализующие их алгоритмы оценивания спектральных и временных параметров сигналов в базисах функций сплайн-характеров (БФСХ). Описывается метод быстрых преобразований сигналов в БФСХ. Обосновывается его высокая вычислительная эффективность. Демонстрируется выигрыш в объеме вычислений при переходе от дискретных экспоненциальных функций к частному случаю БФСХ - базису сплайн-Виленкина-Крестенсона функций (СВКФ). Рассматриваются методы оценивания несущей частоты сигналов на основе глобальных сплайнов. Предлагается алгоритм сплайн-БПФ в базисах функций сплайн-характеров. Анализируется эффективность методов оценивания несущей частоты сигналов с точки зрения точности, скорости и помехоустойчивости обработки. Оцениваются вычислительные затраты на интерполяцию при использовании классического и предлагаемого методов на примере частного случая БФСХ - СВКФ.

Еще

Оценивание параметров сигналов, функции сплайн-характеров, быстрые преобразования сигналов, базис сплайн-виленкина-крестенсона функций

Короткий адрес: https://sciup.org/14264784

IDR: 14264784 | УДК: 621.391

Methods of the estimation of spectral and temporary parameter signal on the basis of the theories of spline algebraic harmonic analysis

The developed methods and realizing them algorithms of the estimation of spectral and temporary parameter signal in base function of spline-character (BFSH) are suggested. The method for quick transformations of signal in these bases is described. Its high computing efficiency is proved. The advantage in calculation volume in passing from discrete exponential function to particular case BFSH - a base spline-Vilenkin-Krestenson functions - is shown. Methods for the estimation of signal carrying frequencies are considered using global splines. The algorithm of spline-BPF is offered in the base functions of spline-character. Efficiency of the methods for the estimation of signal carrying frequencies from the points of view of accuracy, velocities and noise-immunity of the processing is analyzed. The computing expresses on interpolation with the use of classical and proposed methods on the example of the particular case BFSH - SVKF are evaluated.

Еще

Текст научной статьи Методы оценивания спектральных и временных параметров сигналов на основе теории сплайн-алгебраического гармонического анализа

Предлагаются разработанные методы и реализующие их алгоритмы оценивания спектральных и временных параметров сигналов в базисах функций сплайн-характеров (БФСХ). Описывается метод быстрых преобразований сигналов в БФСХ. Обосновывается его высокая вычислительная эффективность. Демонстрируется выигрыш в объеме вычислений при переходе от дискретных экспоненциальных функций к частному случаю БФСХ — базису сплайн-Виленкина-Крестенсона функций (СВКФ). Рассматриваются методы оценивания несущей частоты сигналов на основе глобальных сплайнов. Предлагается алгоритм сплайн-БПФ в базисах функций сплайн-характеров. Анализируется эффективность методов оценивания несущей частоты сигналов с точки зрения точности, скорости и помехоустойчивости обработки. Оцениваются вычислительные затраты на интерполяцию при использовании классического и предлагаемого методов на примере частного случая БФСХ — СВКФ.

Кл. сл. : оценивание параметров сигналов, функции сплайн-характеров, быстрые преобразования сигналов, базис сплайн-Виленкина-Крестенсона функций

ОПРЕДЕЛЕНИЕ СПЛАЙН-ХАРАКТЕРОВ

Пусть имеется пространство функций, заданных на абелевой группе H и принимающих значения в некотором кольце K , т. е. областью определения функций является группа H , областью значений — кольцо K . Это пространство обозначим через L ( H , K ) . Аналогами комплексных экспонент в L ( H , K ) являются характеры χ ( n , k ) [1]. Характеры образуют ортонормированный базис в пространстве L ( H , K ) . Характеры χ ( n , k ) , определенные на конечном отрезке, называются χ -функциями. В дальнейшем для общности будем использовать понятие "характеры", а из контекста будет ясно, о каком случае (конечном или бесконечном) будет идти речь. Одним из достоинств характеров χ ( n , k ) является их многообразие, определяемое многообразием групп H и колец K . Однако все они являются функциями дискретными, поэтому реализация на их основе сигналов для непосредственного излучения в эфир невозможна. Получить гладкие ортонормированные базисные функции оказалось возможным, объединив свойства χ ( n , k ) и сплайнов. В результате в полученном пространстве _L ₍ _H _, _K ₎ G _n ^p периодических сплайнов сигнал _L ₍ _H _, _K ₎ S ^p ( t ) можно разложить следующим образом:

S^P ( t ) = —У , qHKpit^t ( t 0 tk ) =

L ( H , K ) N _k L ( H , K ) k µ k

= У L ( H , K ) cn L ( H , K ) ^ ^p ⁽ t X

где L ( H , K ) ^ ^p( ^t ) = L ( H , K ) m ^p( ^t )/7 L ( H , K ) un p ; L ( H , K ) m t ⁽ t )

=—У x(n,k)Mp(t0tk); X(n, k) — характеры груп-Nk µ пы H ; L(H,K) сп = L(H,K) Fn (z)L(H,K) uPP /L(H,K)Up ;

ц — модуль представления чисел; 0 — сдвиг по мо-µ дулю ц; l(h,k) up = l(h,k) Fn(Mp) = -1 Ух(n, k)Mp (tk);

Nk tk

N ; χ(n, k) — комплексносопряжен- ное χ(n,k) . Заметим, что сплайны

L(H,K) ^p (t) L(H,K) mp (t)/^L(H,K) un P образуют ортонормированный базис пространства L(H,K)Gnp . Будем называть их сплайн-характерами.

ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ В БАЗИСАХ ФУНКЦИЙ СПЛАЙН-ХАРАКТЕРОВ

Для пространств _L ( _HK ) G p (при t = k ) введем пары прямых и обратных преобразований Фурье (ПФ) в базисах функций сплайн-характеров

(БФСХ):

S^p ( к ) = V .. F (q F _n ( q * ) X p ( к ) =

L ( H , K ) L ( H , K ) n L ( H , K ) n

= ^ L ( H , K ) F i ⁽ z ) / L ( H , K ) n

2 p

L ( H , K ) u n L ( H , K )

где

L ( H , K ) F i ⁽ ^q ) = T7^ ^x ⁽ ¹ , ^k ) L ( H , K ) ^q k =

N k

= — S>X ^p ( к ) z, . (3)

n L ( H , K ) k

N _k

X Р ( к ), (2)

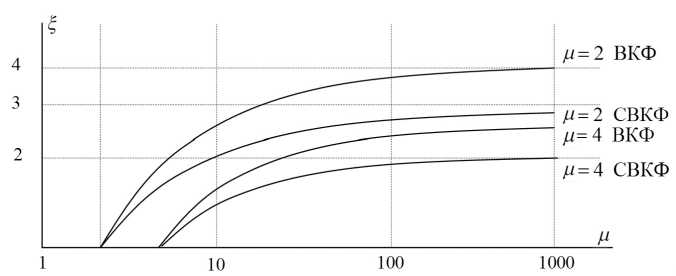
Рис. 1. Выигрыш в объеме вычислений БПФ при переходе от базиса ДЭФ к базисам ВКФ и СВКФ при µ = 2, 4

Отметим, что при p = 1 частными случаями пары выражений (2) и (3) являются выражения, полученные в [1] ((3.9) и (3.10)).

МЕТОД БЫСТРЫХ ПРЕОБРАЗОВАНИЙ СИГНАЛОВ В БАЗИСАХ ФУНКЦИЙ СПЛАЙН-ХАРАКТЕРОВ

Согласно (2), для нахождения спектральных коэффициентов в базисе L ( _HK ) X p необходимо вычислить дискретное ПФ L ( _HK ) F _n ( q * ). Один из вариантов его вычисления — через _L ₍ _H _, _K ₎ F _n ( z ) . Для этого необходимо полученную последовательность _L ₍ _H _, _K ₎ F _n ( z ) поэлементно умножить на последовательность _L ₍ _H _, _K ₎ u _n ² ^p _L ₍ _H _, _K ₎ u _n ^p . Элементы последней последовательности могут быть вычислены заранее, а для вычисления _L ₍ _H _, _K ₎ F _n ( z ) имеются быстрые алгоритмы [1]. Следовательно, переход из базиса функций характеров (БФХ) в БФСХ на выборке длиной N увеличивает количество операций преобразования на N . Это касается как ПФ в БФСХ, так и его быстрого алгоритма.

Таким образом, быстрое преобразование в БФСХ существует, и его основа — алгоритм быстрого преобразования Фурье (БПФ) в БФХ. При этом вычислительная сложность БПФ в БФСХ на выборке длиной N увеличивается на N операций умножения по сравнению с алгоритмом БПФ в БФХ. Сравнение вычислительных затрат классического алгоритма БПФ со всеми алгоритмами БПФ в БФСХ — задача невыполнимая по причине бесконечного количества последних. Поэтому остановимся на некоторых из них.

Сравним вычислительные затраты, требуемые для осуществления алгоритмов БПФ для частного случая БФСХ — базисов сплайн-Виленкина-Крестенсона (СВКФ). Для достижения этой цели воспользуемся подходом, предложенным в [2]. Если принять, что на операцию умножения и сложения тратится одинаковое время, то предельный выигрыш по скорости обработки ξ при использовании быстрого преобразования Уолша (БПУ) относительно дискретных экспоненциальных функций (ДЭФ) в алгоритме БПФ будет достигать ξ = 5. В то же время применение функций Вилен-кина-Крестенсона (ВКФ) по модулю 4 обеспечивает ξ= 3.25. В рассматриваемом случае для получения спектра использовался алгоритм БПФ в базисах СВКФ [3]. Согласно этому алгоритму на N входных точек преобразования, дополнительно к стандартному объему вычислений необходимо добавить N операций умножения. Это приводит к увеличению объема вычислений по сравнению с классическими алгоритмами БПУ и БПФ в базисе ВКФ по модулю 4. Однако получаемый выигрыш в этих случаях по сравнению с использованием классического алгоритма БПФ все равно оказывается существенным.

Данные об объеме вычислений для алгоритма БПФ [4] и результаты [2] позволили представить выигрыш в скорости цифровой обработки сигналов (ЦОС) графиком рис. 1 [5]. Анализ полученных результатов показал, что выигрыш в объеме вычислений при переходе к базису СВКФ может достигать 2÷3 раз.

Таким образом, реализация операций ЦОС с использованием алгоритма БПФ в базисе СВКФ ведет к существенному сокращению вычислительных затрат. Аналогичные результаты можно получить и при рассмотрении алгоритма в базисе сплайн-Рейдера.

АЛГОРИТМ СПЛАЙН-БПФ В БАЗИСАХ ФУНКЦИЙ СПЛАЙН-ХАРАКТЕРОВ

Довольно часто при выполнении стандартных операций ЦОС (фильтрации, вычислении корреляционных функций, определении несущей частоты) возникает необходимость осуществления интерполяции обрабатываемых дискретных данных о непрерывных функциях. Следовательно, возни-

кает необходимость разработки вычислительно эффективного алгоритма интерполяции сигналов. В теории сплайн-гармонического анализа (СГА) таким алгоритмом является алгоритм сплайн-БПФ в ДЭФ [6]. Его вычислительная эффективность базируется на том, что он построен на основе классического БПФ, поэтому по свойствам сравним с известным алгоритмом интерполяции, основанным на добавлении нулевых коэффициентов в спектральной области. Отличие состоит в том, что вместо добавления нулей в спектральной области используется информация о степени гладкости. Это позволяет осуществлять не линейную интерполяцию, как в классическом случае, а соответствующую выбранному порядку сплайна (например, кубическому). Рассматриваемый подход реализации быстрых преобразований позволяет разработать алгоритм сплайн-БПФ (СБПФ) сигналов в БФСХ. Рассмотрим особенности этого алгоритма.

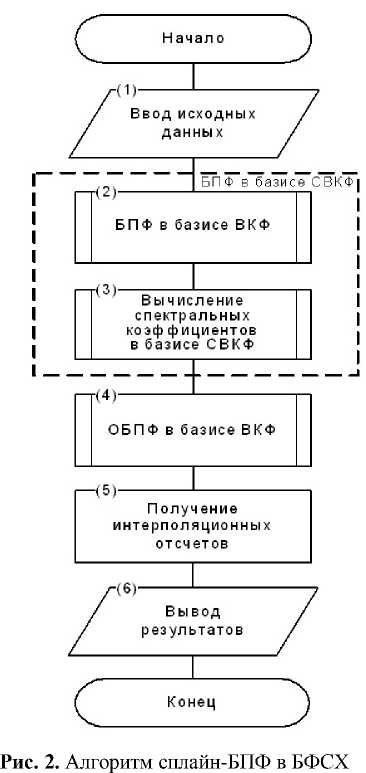
Так как в основе алгоритма сплайн-БПФ в базисе ДЭФ лежат процедуры БПФ, то разумно положить процедуры БПФ в БФСХ в основу алгоритма сплайн-БПФ в БФСХ. Исходными данными для алгоритма (см. рис. 2) являются объем выборки N , порядок сплайна p , тип группы H и кольца K , модуль представления числа ц , отсчеты сигнала { z k } и шаг сетки интерполяции h .

Разработанный алгоритм (рис. 2) отличается от известного не только переходом от ЭФ к БФСХ, но и отказом от увеличения количества спектральных коэффициентов перед осуществлением операции ОБПФ в соответствующем базисе, поскольку получение интерполяционных значений происходит уже во временнóй области. Структурная схема, реализующая указанные процедуры, представлена на рис. 3. В Приложении (табл. 1) представлены сравнительные затраты на интерполяцию при использовании классического и предлагаемого методов на примере частного случая БФСХ — СВКФ.

Анализ полученных результатов показывает, что выигрыш в объеме вычислений может достигать от 1.69 до 2.71 раза даже на коротких выборках сигнала. Таким образом, предложенный алгоритм обладает вычислительной эффективностью и может быть использован для осуществления фильтрации, вычисления корреляционных функций, определения несущей частоты.

Рис. 3. Принцип реализации процедур интерполяции в БФСХ

S^p ( t k _i )

МЕТОД ОЦЕНИВАНИЯ НЕСУЩЕЙ ЧАСТОТЫ В БАЗИСАХ ФУНКЦИЙ СПЛАЙН-ХАРАКТЕРОВ

Большое значение при приеме сигналов имеет оценивание несущей частоты. Для классических моделей сигналов в базисе ДЭФ оценивание осуществляется с использованием ПФ. Однако для сигналов, синтезированных в БФСХ, невозможно правильно оценить несущую частоту на основе базиса Фурье. Естественно, данную операцию необходимо выполнять в БФСХ.

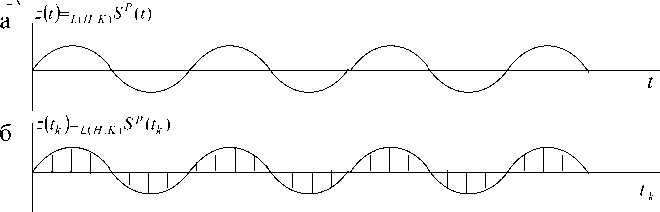
На рис. 4 представлены эпюры, поясняющие принцип оценивания частоты в БФСХ.

Аналоговый сигнал z ( t ) (рис. 4, а) дискретизируют z ( t _k ) (рис. 4, б), затем вычисляют последовательность комплексных спектральных коэффициентов _L ₍ _H _, _K ₎ F _n ( z ) (рис. 4, в) методом преобразования в выбранном пользователем базисе характеров. Одновременно тем же методом В -сплайн заданной степени p - 1 преобразуется в последовательность комплексных дискретных отсчетов

(рис. 4, г). Порядок В -сплайна определяется пользователем и зависит от степени гладкости анализируемого сигнала. Затем последовательность комплексных спектральных коэффициентов _L ₍ _H _, _K ₎ F _n ( z ) делят поэлементно на последовательность комплексных дискретных отсчетов 7 L ( н , K ) u ²p / l ( H , к ) u p Для базисов L ( H , K ) ^X p ⁽ t ) (рис. 4, д). Далее вычисляют компоненты спектральной плотности мощности _L ₍ _HK ) S ( n ) в БФСХ (рис. 4, е) заданной степени p - 1 с помощью выражения, представленного на рис. 4, е, где N — нормирующий множитель. На новом массиве компонент спектральной плотности мощности находится максимум r (рис. 4, ж), а значение несущей частоты сигнала определяется по формуле f n = r ^х f , где ^ f — расстояние между спектральными компонентами X P ( t ).

L ( H , K ) n

Оценим вычислительные затраты рассмотренного подхода. Его основу составляют процедуры

S ( n ) = L ( H , K ) ^Fn ⁽ z )

^p L ( H , K ) u n

L ( H , K ) ^S ⁽ n ) = L ( H , K ) ^F n ⁽ z )

pp L ( H , K ) u n L ( H , K ) u n

,~ ( n ) = N I Re

L ( H , K ) ' 1 I

L ( H , K ) F n ( z )

u p

L ( H , K ) u n J

¹f F (z))² + | Im ^L ( ^^K ) n ( )

u p

L ( H , K ) u n J

1 2

r r + 1 + 2

Рис. 4. Принцип оценивания несущей частоты в БФСХ n

БПФ в БФСХ. Сокращения объема вычислений данной процедуры возможно за счет формирования сигналов в базисах сплайн-Рейдера, в СВКФ с использованием модуля 2…4. В этом случае вычислительные затраты сократятся в 2…3 раза.

МЕТОДЫ ОЦЕНИВАНИЯ НЕСУЩЕЙ ЧАСТОТЫ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ

АЛГОРИТМА СПЛАЙН-БПФ В БАЗИСАХ ФУНКЦИЙ СПЛАЙН-ХАРАКТЕРОВ

Дальнейшее повышение вычислительной эффективности и точности оценивания возможно за счет учета информации о гладкости спектральной плотности мощности сигналов. Поскольку точность оценивания определяется величиной частотного разрешения, то необходимо повысить разрешающую способность. При классическом подходе это достигается за счет увеличения длины реализации сигнала, в том числе и путем добавления нулевых значений. При этом существенно растет объем вычислений, а интерполяция осуществляется по линейному закону без использования информации о степени гладкости спектральной плотности мощности сигнала. В связи с этим предлагается использовать сплайн-интерполяцию в частотной области. Причем эту операцию предлагается проводить с помощью вычислительно эффективного алгоритма сплайн-БПФ в БФСХ. Возможны два варианта интерполяции [7].

В первом случае используются коэффициенты всей реализации. Во втором — интерполяция производится только вблизи исходного максимального спектрального коэффициента. Эффективность указанных методов оценивалась с позиций скорости ЦОС (Приложение, табл. 2).

Характеристика методов по точности определения несущей частоты сигналов представлена в Приложении, табл. 3. Согласно табл. 3, чем выше степень гладкости интерполируемого процесса, соответственно и степень гладкости сплайна, тем выше точность интерполяции [8]. Если h = 0.1, то точность кубической интерполяции с использованием глобальных сплайнов будет пропорциональна 0.0001. При классическом подходе точность интерполяции пропорциональна h = 0.05 или необходимо значительное увеличение объема вычислений.

Важно отметить, что использование глобальных сглаживающих сплайнов может повысить помехоустойчивость определения несущей частоты. Согласно табл. 3 (см. Приложение), при выборе кубического сплайна выигрыш в помехоустойчивости может достигать 0.5 дБ.

МЕТОДЫ ОЦЕНИВАНИЯ НЕСУЩЕЙ ЧАСТОТЫ С ИСПОЛЬЗОВАНИЕМ ЛОКАЛЬНЫХ

СПЛАЙНОВ

Основное отличие локальных сплайнов от глобальных состоит в том, что для интерполяции используется значительно меньший объем информации. Например, для поиска экстремума достаточно данных лишь о вблизи расположенных отсчетах сигнала. Это относится и к простейшим сплайнам, таким как сплайны минимального шаблона (СМШ), квадратичные (КВСМШ) и кубические (КСМШ), квазиинтерполяционные сплайны (КИС), сплайны максимального сглаживания (СМС) [9]. Однако обеспечиваемая ими точность и помехоустойчивость ниже по сравнению с глобальными сплайнами, а вычислительная эффективность существенно изменяется в зависимости от длины реализации.

Представление о вычислительной эффективности простейших сплайнов на примере СМШ с использований экспоненциальных функций и СВКФ с модулем 2 и 4 дает табл. 4 (в Приложении). Характеристика точности определения несущей частоты сигналов представлена в Приложении в табл. 5.

Анализ полученных результатов показал, что при выборе наиболее часто используемого кубического СМС выигрыш в помехоустойчивости может достигать 0.22 дБ.

МЕТОД ВЫЧИСЛЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СИГНАЛОВ

Предлагаемый метод базируется на свойствах сплайнов и предложенного алгоритма СБПФ. Его вычислительная эффективность обеспечивается при условии расчета корреляционной функции при предельно низкой частоте дискретизации. Вариант структурной схемы, реализующий метод, в соответствии с указанными требованиям, представлен на рис. 5.

Сравнительные затраты на вычисление корреляционных функций при использовании различных базисов представлены в Приложении в табл. 6. При этом интерполяция на Л- N точках производится для получения дополнительных значений корреляционной функции на всей ее области определения. А интерполяция на Л- 2 точках производится только в районе максимума. Здесь λ — количество точек интерполяции между двумя узловыми точками, N (2) — количество интервалов интерполяции, 4 — количество операций для получения одного интерполируемого значения. Полученные результаты подтверждают вычислительную эффективность предложенного алгоритма.

Рис. 5. Вычисление автокорреляционной функции в БФСХ

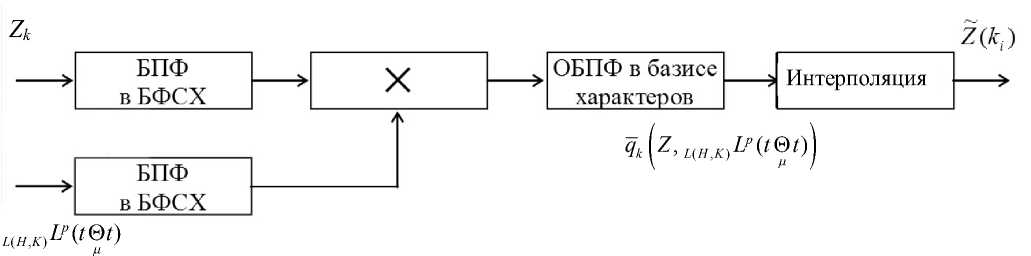
Рис. 6. Фильтрация в базисах СВКФ

МЕТОД ФИЛЬТРАЦИИ СИГНАЛОВ В БАЗИСАХ ФУНКЦИЙ СПЛАЙН-ХАРАКТЕРОВ

Вариант структурной схемы метода фильтрации сигналов в базисах функций сплайн-харак-теров представлен на рис. 6. Вычислительная эффективность метода фильтрации — в Приложении, табл. 7.

В основе разработанного метода лежит использование алгоритма СБПФ в БФСХ. Анализ полученных результатов показывает, что даже без интерполяции выигрыш в объеме вычислений достигает от 1.45 до 2.86 раза на коротких выборках сигнала. Данный факт подтверждает вычислительную эффективность разработанного метода.

ЗАКЛЮЧЕНИЕ

Разработана аналитическая основа методов оценивания спектральных и временных параметров сигналов в БФСХ.

Предложен метод быстрых преобразований сигналов в БФСХ, обладающий высокой вычислительной эффективностью. Выигрыш в объеме вычислений при переходе от ДЭФ к частному случаю БФСХ — базису функций сплайн-Виленкина-Крестенсона — достигает 2…3 раз.

На основе разработанного алгоритма сплайн-БПФ в БФСХ предложены методы оценивания несущей частоты сигналов с использованием глобальных сплайнов. Вычислительная эффективность указанных методов для СВКФ достигает 2.54 раза и более даже на коротких выборках сигнала. А выигрыш в помехоустойчивости для сглаживающих глобальных сплайнов может достигать 1 дБ.

Использование методов оценивания несущей частоты сигналов на основе локальных сплайнов может обеспечить выигрыш в помехоустойчивости до 0.5 дБ при достаточно высокой вычислительной эффективности.

При расчете корреляционных функций сигналов вычислительные затраты по сравнению с классическим подходом для СВКФ как частного случая БФСХ сокращаются в 2.1 и более раза.

Выигрыш в объеме вычислений при фильтрации сигналов может достигать от 1.45 до 2.86 раза даже на коротких выборках сигнала по отношению к классическому подходу.

Таким образом, применение разработанного аналитического аппарата обработки сигналов обеспечивает повышение помехоустойчивости при общем снижении вычислительных затрат.

ПРИЛОЖЕНИЕ

Табл. 1. Количество операций на интерполяцию различными методами в базисах СВКФ (квадратичный сплайн)

Параметры метода								Количество операций
N	cd й О S У га S	в а о о в В	е m CJ о S ю га е и	о 9 pq VO Q ОД К 5 CJ	в к И -X К s О В ^ В" о 5 в о в в о «	е m cd О од ^ е О	е m о И ст о в ю е О	О Cl g О й 2 в g в § в 2 о	о CJ m	а & m
64	ЭФ	Доб. нулей	384	–	8	–	4608	–	4992	–
64	ЭФ	СБПФ	384	128	8	384		2048	2944	1.69
64	2	СБПФ	192	64	8	192	–	2048	2496	2
64	4	СБПФ	256	128	8	256	–	2048	2688	1.85
128	ЭФ	Доб. нулей	896	–	8	–	10240	–	11136	–
128	ЭФ	СБПФ	896	256	8	896		4096	6144	1.81
128	2	СБПФ	407	128	8	407	–	4096	5038	2.21
128	4	СБПФ	535	256	8	535	–	4096	5422	2.05
256	ЭФ	Доб. нулей	1024	–	8	–	22528	–	23552	–
256	ЭФ	СБПФ	1024	512	8	1024		8192	10752	2.19
256	2	СБПФ	410	256	8	410	–	8192	9268	2.54
256	4	СБПФ	552	512	8	552	–	8192	9808	2.44
512	ЭФ	Доб. нулей	4608	–	8	–	49152	–	53760	–
512	ЭФ	СБПФ	4608	1024	8	4608	–	16384	26624	2.01
512	2	СБПФ	1440	512	8	1440	–	16384	19776	2.71
512	4	СБПФ	2355	1024	8	2355	–	16384	21658	2.48

Табл. 2. Количество операций на интерполяцию при определении несущей частоты различными методами в базисах СВКФ (кубический сплайн)

Параметры метода										Число операций на интерполяцию
	cd о У вР $ S	к	S1 о о в в в	н 6 И В о В" и ст ⁸ ц ю о ® Рн	га га S X § cd to	к о и 5	е га СО cd to	га К со cd to	е е ® о ! ю m	λN /2	λN	λ ∙2	О о m	а & m
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
64	ЭФ	Нулями	8	4608	–	9216	–	–	–	–	–	–	13824	–
64	ЭФ	СБПФ	8	384	64	128	160	64	160	1280	–	–	2240	6.17
64	ЭФ	СБПФ	8	384	64	128	160	64	160	–	–	80	1040	13.26
64	2	СБПФ	8	110	64	64	110	64	110	–	2560	–	3082	4.48
64	2	СБПФ	8	110	64	64	110	64	110	–	–	80	602	22.96

Табл. 2 ( продолжение )

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
64	4	СБПФ	8	192	64	128	84	64	84	1280	–	-	1896	7.29
64	4	СБПФ	8	192	64	128	84	64	84	–	–	80	696	19,86
128	ЭФ	Нулями	8	10240	–	20480	–	–	–	–	–	–	30720	–
128	ЭФ	СБПФ	8	896	128	256	384	128	384	2560	–		4736	6.48
128	ЭФ	СБПФ	8	896	128	256	384	128	384	–	–	80	2256	13.61
128	2	СБПФ	8	230	128	128	230	128	230	–	5120		6194	4.95
128	2	СБПФ	8	230	128	128	230	128	230	–	–	80	1154	26.62
128	4	СБПФ	8	390	128	256	192	128	192	2560	–	–	3846	7.98
128	4	СБПФ	8	390	128	256	192	128	192	–	–	80	1366	22.48

Табл. 3. Интерполяционные и сглаживающие свойства глобальных сплайнов

Метод интерполяции	Потенциальная точность интерполяции	Требование к функции	Выигрыш в помехоустойчивости, дБ
Добавление нулей	1 2 h	_С 1	–
Квадратичная интерполяция	4 (4) max	_С 4	-
Квадратичное сглаживание	4 (4) max	_С 4	0.3
Кубическая интерполяция	< o( h ⁵ z _m ⁽⁵ _a ⁾ _x ) 5/384( h ⁴ z m⁽⁴a⁾x )	С 5	-
Кубический сглаживающий сплайн	< o( h ⁵ z _m ⁽⁵ _a ⁾ _x ), 5/384( h ⁴ z m⁽⁴a⁾x )	С 5	0.5
Интерполяционный сплайн 4-й степени	6 (6) max	С ⁶	-
Сглаживающий сплайн 4-й степени	6 (6) max	_С 6	0.9
Интерполяционный сплайн 5-й степени	7 (7) max	С ⁷	-
Сглаживающий сплайн 5-й степени	7 (7) max	_С 7	1.1

Табл. 4. Количество операций на интерполяцию при определении несущей частоты различными методами c использованием локальных сплайнов

Параметры метода							Число операций на интерполяцию
N	cd ч О S F i-Q О	s	s1 ^н Ц о о ц В a ^ в в	6 н 6 =- и В" и cd ⁸ и ю Рн	и S 5* X у Ю	S и 5	Одной точки	λ ∙ N /2	λ ∙ N	λ ∙∙2	О о	а в & в В m
64	ЭФ	Доб. нулей	8	4608	–	9216	–	–	–	–	13824	–
64	ЭФ	КВСМШ	8	384	32	128	21	5376	–	–	5920	2.33
64	ЭФ	КВСМШ	8	384	32	128	21	–	–	336	880	15.7
64	ЭФ	КСМШ	8	384	32	128	28	7168	–	–	7712	1.79
64	ЭФ	КСМШ	8	384	32	128	28	–	–	448	992	13.93
64	ЭФ	СМШ 4-й степени	8	384	32	128	80	20480	–	–	21024	0.66
64	ЭФ	СМШ 4-й степени	8	384	32	128	80	–	–	1280	1824	7.58
64	ЭФ	СМШ 5-й степени	8	384	32	128	102	26112	–	–	26656	0.52
64	ЭФ	СМШ 5-й степени	8	384	32	128	102	–	–	1632	2176	6.35
64	ЭФ	КИС 5-й степени	8	384	32	128	175	44800	–	–	45344	0.3
64	ЭФ	КИС 5-й степени	8	384	32	128	175	–	–	2800	3344	4.13
64	ЭФ	СМС 5-й степени	8	384	32	128	175	44800	–	–	45344	0.3
64	ЭФ	СМС 5-й степени	8	384	32	128	175	–	–	2800	3344	4.13
64	ЭФ	Доб. нулей	8	390	128	256	–	–	–	–	13824	–

Табл. 5. Интерполяционные и сглаживающие свойства локальных сплайнов для различных методов оценивания несущей частоты

Метод интерполяции	Потенциальная точность интерполяции	Требование к функции	Выигрыш в помехоустойчивости, дБ
1	2	3	4
Добавление нулей	1/(2 h )	_С 1	–
КВСМШ	0.047 h ³ z m⁽³a⁾x	С ⁴	-
Квадратичный КИС	< 0.047 h ³ z m⁽³a⁾x	_С 4	-
Квадратичный СМС	0.047 h ³ z m⁽³a⁾x	_С 4	0.1
КСМШ	35/1152 h ⁴ z m⁽⁴a⁾x	С ⁵	-
Кубический КИС	< 35/1152 h ⁴ z m⁽⁴a⁾x	С 5	-

Табл. 5 ( продолжение )

1	2	3	4
Кубический СМС	35/1152 h ⁴ z m⁽⁴a⁾x	С 5	0.22
СМШ 4-й степени	132677/13271040 h ⁵ z ⁽⁵⁾max	С 5	-
КИС 4-й степени	< 132677/13271040 h ⁵ z ⁽⁵⁾max	_С 6	-
СМС 4-й степени	132677/13271040 h ⁵ z ⁽⁵⁾max	С ⁶	0.34
СМШ 5-й степени	59/5120 h ⁶ z m⁽⁶a⁾x	_С 7	-
КИС 5-й степени	< 59/5120 h ⁶ z m⁽⁶a⁾x	_С 7	-
СМС 5-й степени	59/5120 h ⁶ z m⁽⁶a⁾x	С ⁷	0.5

Табл. 6. Количество операций на вычисление корреляционных функций в базисах СВКФ

N	§ 6 I	m О 8 в 1 и	eg й 8 о 3 § 5 у И В g g	§ I &	и	m о 8 о ^	8 «§ * 6 2 g^	Количество операций на интерполяцию		Всего	Выигрыш
	§ 6 I	m О 8 в 1 и	eg й 8 о 3 § 5 у И В g g	§ I &	и	m о 8 о ^	8 «§ * 6 2 g^	На λ ∙ N точках	На λ ∙2 точках
64	ЭФ	384	–	384	8	–	4608	–	–	5376	–
64	2	192	64	64	8	192	–	2048	64	2560/576	2.1/9.33
64	4	256	64	384	8	256	–	2048	64	3008/1024	1.78/5.25
128	ЭФ	896	–	768	8	–	10240	–	–	11904	–
128	2	407	128	128	8	407	–	4096	64	4806/1134	2.48/10.5
128	4	535	128	768	8	535	–	4096	64	6062/2030	1.96/5.86
256	ЭФ	1024	–	1536	8	–	22528	–	–	25088	–
256	2	410	256	256	8	410	–	8192	64	9124/996	2.75/25.19
256	4	552	256	1536	8	552	–	8192	64	11088/2960	2.26/8.48
512	ЭФ	4608	–	3072	8	–	49152	–	–	56832	–
512	2	1440	512	512	8	1440	–	16384	64	20288/3968	2.8/14.32
512	4	2355	512	3072	8	2355	–	16384	64	24678/8358	2.3/6.8

Табл. 7. Количество операций на фильтрацию в различных базисах (без интерполяции)

N	Модуль числа	БПФ в базисе ВКФ (операций)	Вычисление спектральных коэффициентов сигнала, прошедшего через фильтр	ОБПФ в базисе ВКФ N точек	Всего	Выигрыш
1	2	3	4	5	6	7
64	ЭФ	384	64	384	832	–
64	2	192	64	192	448	1.86

Табл. 7 ( продолжение )

1	2	3	4	5	6	7
64	4	256	64	256	575	1.45
128	ЭФ	896	128	896	1920	–
128	2	407	128	407	943	2.04
128	4	535	128	535	1198	1.6
256	ЭФ	1024	256	1024	2304	–
256	2	410	256	410	1075	2.14
256	4	552	256	552	1360	1.69
512	ЭФ	4608	512	4608	9728	–
512	2	1440	512	1440	3392	2.86
512	4	2355	512	2355	5222	1.86