Методы определения несущей способности монолитных шпоночных соединений сборных элементов

На сегодняшний день проведено большое количество экспериментальных и теоретических исследований шпоночных соединений железобетонных сборных конструкций с целью определения предельного сдвигающего усилия в шве Тш. Выделяют характерные виды разрушения шпонок в соединении [1]: сдвиг по опорной грани шпонки; смятие опорной грани; срез по основанию шпонки; срез по наклонной трещине.

Смещение по опорной грани не происходит при углах наклона шпонок а < 35° (рис. 1) и является ошибкой конструирования соединения, поэтому указанный вид разрушения не рассматриваем.

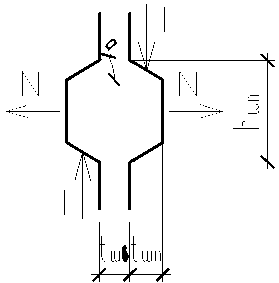
Рис. 1. Схема шпоночного соединения [1]

Прочность бетонной шпонки при скалывании и при смятии регламентируют действующие нормы [4, 5]. При расчете на смятие:

Тсм = Нь.юсАсм, где Rb-loc = Rb, при бетоне класса В25 и ниже, и Rb-loc = 13,5Rbt — для бетонов классов выше В25, Лсм - площадь смятия шпонки.

В [2, 3] указанная фор м ула повтор я ется, однако величина R_b>loc = R_b д ля многош п оночных соединений, и R_b-loc = 1,5R_b - для одношпоночного.

При расчете на срез по нормативным документам [4, 5]:

Тср = YсрRbtAср, здесь y„„ = 1,5 [1], автор [5] предлагает принимать ср

Y = п/2; R_bt - прочность бетона на ра с тяжение; ср

Л_ср - площадь среза шпонки. В первом случае коэффициент Y_с p получен путем статистической обработки испытаний, во втором - теоретическими выкладками исходя из прочности бетонных образцов на раскалывание. При расчете на образование нак л онной трещины:

Тнак = YнaкRbtSkt, где коэффициент Yнак = ^шп/(tшв + tшn) [4] или Yнак = 0,7 в [5]; sk - шаг шпонок и t - толщина замоноличенной поверхности (например, толщина стены).

За несущую способность шпонки Тшп принимают наименьшее значение Тня„, Т™ или Т„.

нак , ср см

При воздействии сил сдвига возникает распорное усилие Н [1], при этом его величина равна к_аТ и изменяется в зависи м ости от геометриче-

Краткие сообщения ских размеров от 0,157 до 0,27. Распор должен быть воспринят нормальным армированием.

При расчете несущей способности шпонки с учетом примыкающих участков сдвига [1, 3] рекомендуют использовать формулу

⁷ = ⁷ шп ⁽¹ - Мдф) + ^tgф(Ц_попй_s ,поп + G)S_kt, здесь ц_поп = A_s/(s_kt) - коэффициент поперечного армирования, R_S1ПOП - расчетное сопротивление поперечной арматуры, σ – напряжения обжатия стыка в перпендикулярном ему направлении.

При этом значение 7 не должно превышать максимально го, рассчитываемого по формуле ⁷ тах ^_ tS_k^R bt (R bt + Р поп^поп + о) <  ts_k • 2R_bt .

Последнее выражение было получено исходя из прочности по главным растягивающим напря- жениям.

Минимальное количество продольной арматуры определяется минимальной величиной рас- пора:

Р_поп т1п ^ a ⁷ шп ^/(Rs, поп ^tsk^{) .}

Кроме того в нормах [2] отмечено, что суммарное сопротивление сдвигу железобетонного шпоночного соединения не должно превышать

7 „ нак

(°^ст + ^5,поп^5,поп+^5,прод^5,прод)5к tшв+tшп здесь Лст - площадь среза всего стыка, Л5-прод

и

Rs,прод — соответственно суммарная площадь и расчетное сопротивление продольной арматуры в стыке. Последняя величина принимается равной рас- четному сопротивлению растяжению арматуры при расчете наклонных сечений на действие поперечной силы Rsw, в случае если продольное армирование представлено одним стержнем Rs,прод = Rs.

Расчет несущей способности шпоночных соединений предусмотрен также и европейскими нормами [7, 8]. Расчетное сопротивление шпоночного соединения сдвигу равно:

V_Rdt = cf_c td + tgФ • о „ + ц_попf yd (tgф sin9 + cos9), где с и tgф - коэффициенты, зависящие от шероховатости границы взаимодействия и равные для шпоночного соединения с = 0,5 и tgф = 0,9; f_ctd - расчётное сопротивление бетона растяжению;о_п - нормальное усилие сжатия в стыке; f_yd - расчетное сопротивление поперечной арматуры; θ – угол наклона поперечной арматуры к плоскости сдвига.

Автором [9] путем анализа кругов Кулона – Мора и отношений, полученных Друккером, как критериев напряженно-деформированного состояния бетона при двухосном НС, удалось получить формулы для определения несущей способности шпоночного соединения при сдвиге:

т = 7/Аст = fc Jo^v ^ - ap), где ap = (AS|попfyd)/(AeIfc), v = 0,55 - коэффициент, учитывающий пластические свойства бетона; ^шп - отношение площадей среза шпонок ЛСт к площади стыка. Это отношение верно при a < у^шп 1 51пв, где р _ 45° _ угол внутреннего Лст     2

трения для бетона. При ap >  ^у^ ^{шп 1 51пв} применя- Л ст      2

ется зависимость

т _ — _ f(v — ^^пв + ap tgP).

Лст     С 4 Лст 2СО5в 1

Автор обнаружил, что зависимость т от f_c (a_p) имеет большую сходимость с опытными данными.

Тайские исследователи [10] провели серию экспериментов и построили следующую линейную зависимость:

7 = 0,073Л шп й + 0,82Л s,поп R s,поп , где R - кубиковая прочность бетона омоноличива-ния стыка.

Группа исследователей из США и Канады [11] получили следующие зависимости, подтвержденные экспериментами:

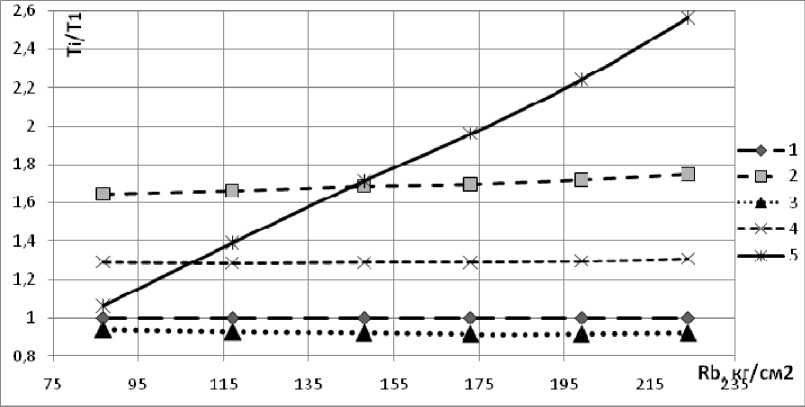
Рис. 2. Несущая способность шпоночного соединения: 1 – рассчитанная по отечественным нормам [1–5]; 2 – по Еврокодам [7, 8]; 3 – по теории Дженсена [9]; 4 – по результатам [10]; 5 – по результатам [11]

Дербенцев И.С.

Методы определения несущей способности монолитных шпоночных соединений сборных элементов величина несущей способности по трещино-образованию:

V cr = V f + V b , где V f - несущая способность стыка, обусловленная силами трения по контакту монолитного и сборного бетонов; V b - сопротивление стыка образованию наклонных трещин в шпонках;

V_CT = Цо_п(Л_с - ndt tan0) + ^f_t(f t + nJ • А_ст, здесь р - коэффициент трения бетона о бетон, принимаемый равным 0,6; о_п - нормальные напряжения сжатия, вызванные обжатием стыка в перпендикулярном направлении; А_с = tH - площадь стыка в продольном направлении (t - толщина стены, H - длина стыка); n, d, tan0 - соответственно количество шпонок в стыке, их глубина и тангенс угла наклона граней; f_t - расчетное сопротивление бетона омоноличивания растяжению (авторами принята зависимость от расчетного сопротивления сжатию f_u: f_t = 0,6^f J ); А_сг = nt^h ? + b² - площадь поперечного сечения образующихся диагональных трещин в шпонках многошпоночного соединения.

Используя приведенные выше формулы, были построены графики несущей способности стыка в зависимости от призменной прочности бетона его омоноличивания (рис. 2), где Т \ - несущая способность соединения, рассчитанная по отечественной методике.

Выводы

• 1.    Методика, полученная отечественными исследователями, отражает варианты разрушения шпоночного соединения и получена на основе наибольшего числа экспериментальных исследований.

• 2.    Схожие результаты дает теория Дженсена [9], хоть и имеет в своей основе иные предпосылки.

• 3.    Формула, заложенная в Еврокодах, дает завышение несущей способности на 70 % по сравнению с отечественными нормами, кроме того она учитывает вероятный наклон поперечной арматуры.

• 4.    График, полученный по [11] существенно отличается от остальных. Это, по-видимому, связано с тем, что испытывались соединения с часто расположенными шпонками, работа которых принципиально другая. Указанная теория учитывает работу бетонного соединения после образования наклонных трещин.

• 5.    Исследователи [10] получили эмпирическую зависимость с запасом 30 %, подтверждающую в целом отечественную методику оценки несущей способности.