Методы определения рассеяния обмоток трансформатора по отдельности

Актуальность проблемы определения рассеяния обмоток трансформатора по отдельности обусловлена той важной ролью, которую играют сопротивления рассеяния в силовых трансформаторах. В аварийных режимах индуктивность рассеяния ограничивает уровни токов коротких замыканий и интенсивность нагрева обмоток, способствует уменьшению электродинамических усилий, благодаря чему снижается вероятность повреждения силового трансформатора при коротких замыканиях (внутренних и сквозных). С другой стороны, с индуктивностью рассеяния связаны добавочные потери в элементах конструкции трансформатора, что уменьшает его полезную мощность, КПД, напряжение на вторичных обмотках и обусловливает потребление реактивной мощности ( Sima et al., 2019; Селиванов и др., 2018 ).

Суммарное реактивное сопротивление рассеяния трансформатора с концентрическими цилиндрическими обмотками равно rnunnDw2 ( a.       a i

x = ——---- — + an + — , l ( 3     0 3 J где ω – циклическая частота тока; µ0 – постоянная магнитная; D – средний диаметр обмотки; w – число витков (приведенное); l – высота обмотки; a0 – зазор между катушками; a1, a2 – толщины катушек (Копылов, 1986).

Существующие методы не позволяют измерять реактивные сопротивления рассеяния для каждой обмотки в отдельности, поэтому полагают их равными половине величины, полученной при расчете по формуле (1) ( Бердников, 2006; 2005 ).

В действительности, применительно к рассматриваемому случаю, они существенно не равны. Потокосцепление внешней обмотки определяется по формуле a   aa2

Ho™D      W                   w2 w2       z^onDw ( a,a,

T 2 =---- w₂z — xdx + w₂zw₂dx + — x — xdx =-------1--+ a ₀ + — I ,

L 10     A1        0             0 a2 a2     J L I 23

где i – приведенный ток, а w1 = w2 = w (индексы показаны для наглядности интегрирования) (Марквардт, 1935). Отсюда реактивное сопротивление рассеяния внешней обмотки равно x2

шц ₀ nDw ² l

a,           a, i

+ an +.

2     ⁰ 3 )

Вычитание его значения из величины, полученной при расчете по формуле (1), дает реактивное сопротивление рассеяния внутренней обмотки x1

ω µ ₀ π Dw ² a ₁

.

l6

Этот результат получен Е. Г. Марквардтом ( Марквардт, 1938 ), но он не имел признания из-за отсутствия экспериментальной проверки.

Знак "–" в выражении (3) указывает на два обстоятельства: 1) внутренняя обмотка поглощает магнитный поток ( Zhao et al., 2019; Попов, 2009 ) в большей степени, чем рассеивает (рассеивает свой, поглощает от внешней обмотки); 2) ее (эквивалентное) реактивное сопротивление рассеяния является емкостным.

Другими словами, рассеяние магнитного потока порождает индуктивное сопротивление, следовательно, противоположный процесс – поглощение магнитного потока – порождает противоположное по характеру емкостное реактивное сопротивление.

Потокосцепление внутренней обмотки с собственным потоком (в области a ₁ ) имеет вид

Ψ

1-1

i µ ₀ π Dw ² a ₁

/ т,

т. е. рассеивает поток. Ее же потокосцепление с потоком внешней обмотки (в области a 1 ) равно

^Ψ 1-2

-

i µ ₀ π Dw ² a ₁

l2

.

Данный поток противоположен, следовательно, внутренняя обмотка его не рассеивает, а поглощает, и этот поток по абсолютной величине больше первого. Таким образом, суммарное потокосцепление отрицательное и реактивное сопротивление рассеяния внутренней обмотки является емкостным.

Из выражений (2) и (3) следует

L ₂

ц ₀ nDw ²

l

a,          a, 1

--+ a₀ + , 2      0 3 j

^C 1 ⁼

6l ω ² µ ₀ π Dw ² a ₁

При экспериментальном определении активных сопротивлений R ₁ и R ₂ обмоток не возникает никаких проблем ( Данилин и др., 2016 ).

Реактивное сопротивление рассеяния любой обмотки определяется из формулы

22 x = Vz - r .

Полное сопротивление z , казалось бы, можно определить в соответствии с законом Ома для участка цепи. Однако при коротком замыкании, когда принято измерять реактивное сопротивление рассеяния, напряжение на вторичной обмотке равно нулю, что является причиной, не позволяющей раздельно измерять рассеяния обмоток. Данную проблему можно решить, используя несколько способов.

Целью настоящего исследования являлось обоснование возможности экспериментального определения реактивных сопротивлений рассеяния для каждой обмотки в отдельности и, в частности, верификации выражений (2)–(5).

Методы исследования

В процессе исследования применялись электротехнические расчеты. Существующие измерительные комплексы позволяют определять действующие значения электрических величин и фазные сдвиги между ними практически с любой заданной точностью. Однако при поочередных измерениях величин высокая точность каждого измерения не имеет большого значения, поскольку сами измеряемые величины нестабильны. При определении реактивных сопротивлений важны не столько величины токов и напряжений, сколько соотношения между ними. Проблема с их нестабильностью решена одномоментной регистрацией необходимых параметров, осуществляемой процессором, что обеспечивает точность вычисляемых величин, сопоставимую с точностью единичного измерения.

Результаты и обсуждение

Высокоточный метод холостого хода

Из схемы замещения трансформатора (рис. 1) следует, что приведенное напряжение на вторичной обмотке равно i ii и2 = и0 = Io .

Отсюда i ii ii i

Uzi = U1 - U0 = U1 - U 2= I1Z1, ii

_ U i - U 2

Zl                           •

1 _i

I 1

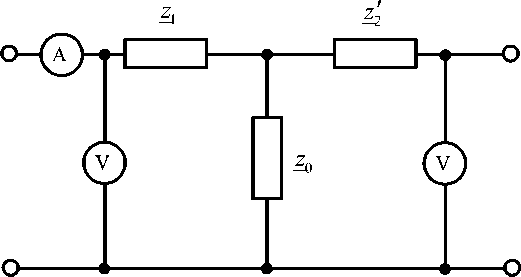
Рис. 1. Схема замещения трансформатора

Fig. 1. Transformer equivalent circuit

Из обратимости трансформатора следует ii

z

² U 2 ′- ² U 1

.

i

I 2 ′

Здесь и далее верхний левый индекс 2 указывает, что величина получена во втором (обратимом) эксперименте.

Пример 1 . Определить сопротивления рассеяния обмоток трансформатора ОСМ-1.00, используя

i

i

i

измеренные с высокой точностью величины ( U 1 = 219,138 В; U 2 = 219,054е ^j0,23 ° В; I 1 = 0,819e ^j80’¹² ° А;

i

2 U 2 = 218,825 В;

i

i

2 U 1 = 218,343e ^j0 - ⁰² ° В; I ’ = 0,817 e - ^j80 - ³² ° А):

ii z = U i - U 2

219,138 - 219,054e ^j0,23 °

i

I 1

0,819 е^-Ж12 °

= 1,075e ^-j433 ° Ом,

r 1 = 1,072 Ом,

C 1 =

x ₁

—1

0,081 Ом, 1

--=----------

2 n fX 1    2n- 50 ■ 0,081

= 0,039 Ф,

i

,   2u2- z-^ =-------- 2i

i

2 U 1    218,825 - 218,343e ^j0-⁰² °

0,817e - j^80,32 °

= 0,601 е 9³⁹ ° Ом,

L 2 =

r2= 0,211 Ом, x2 = 0,562 Ом, x2 = -0562- = 1,790 -10-3 Гн. 2nf 2п50

Пример 2 . Определить сопротивления рассеяния обмоток трансформатора ОСМ-1.00, используя

i

i

величины, измеренные с точностью, уменьшенной на порядок ( U 1 = 219,14 В; U 2 = 219,05e ^j02 ° В;

i

I 1 = 0,82e"^w° А ):

ii _z = U i - U ‘

219,14 - 219,05e ^j0-2°

i

I 1

0,82е"жх°

= 1,44 _e ^j39-⁹° Ом,

r1 = 1,1 Ом, x1 = +0,92 Ом.

Как показывают расчеты, понижение точности на порядок мало сказалось на определении активного сопротивления внутренней обмотки, однако привело к совершенно недостоверному значению реактивного сопротивления, включая смену его знака.

Таким образом, точность измерений в примере 1 (а также 3 и 4) является минимально необходимой.

Высокоточный метод короткого замыкания

Из схемы замещения трансформатора следует, что ii   i

U 0 = I _o z = I 2 z 2 ,

i

^2- z z .

0 i2

I 0

Полное сопротивление при коротком замыкании равно

zz ^        I‘ I^²

z = zi +-----; = z1 + -y—,-------= z1 + zo + ^2        I' Tz' + z’

i z = U

i

I 1

i

--²— z ‘ = z +

i i2        1

1 2 + 1 о

i

1 2 - = z + — z ‘. 1 i2

I 1

Отсюда

ii

z 1 = ^U i1

I 1

-

I 2 z ′ .

i2

I 1

Из обратимости трансформатора следует

z

i

i

12 v

iii

1 2 + I - 1 2

I1

i

₅= U

I 1

i ( i