Методы отбора корней из заданного множества в тригонометрических уравнениях

Тригонометрическое уравнение - это уравнение, содержащее тригонометрические функции неизвестного аргумента [1]. Множество всех корней данного уравнения обычно бесконечно. Но, если задан отрезок, интервал или полуинтервал, всегда можно отобрать конкретные корни тригонометрического уравнения. Рассмотрим три метода отбора корней из заданного множества: геометрический, алгебраический, функциональный.

Геометрический метод - это такой метод отбора корней, когда чертят единичную окружность, отмечают заданный промежуток и находят на нем корни данного уравнения. Рассмотрим геометрический метод при решении тригонометрического уравнения в едином государственном экзамене по профильной математике в примере 1.

Пример 1:

• а) . Решите уравнение cos2x = sin( x + | )

• б) . Найдите корни этого уравнения, принадлежащие промежутку: [-2п; - п] [2].

Решение:

• а) . Преобразуем правую часть уравнения с помощью формулы приведения: sin( х + | ) = cosx, тогда cos2x = cosx

Для преобразования левой части необходимо применить формулу двойного       угла:         cos2x = (cosx)² — (sinx)² = 2(cos x)² — 1.

Получаем: 2(cosx)2 — 1 = cosx.

Перенесем все в левую часть уравнения: 2(cos x)² — cosx — 1 = 0.

Обозначим cosx = t, где —1 <  t < 1, тогда 2t 2 -1 - 1 = 0.

Решаем данное квадратное уравнение: D = b2 — 4ac = (—1)2 — 4 • 2 • (—1) = 1 + 8 = 9.

—ь + VD  —(—1) + V9 1 + 3

• t1 =   2а =    2^2    =  4=

—ь — VD  —(—1) — V9 1 — з1

• t2 = 2a =    2^2    =  4=

  Обратная замена: cosx = 1, cosx =

  
  

  —

  
  
  
  

cosx = 1

Х1 = 2лгг, где n — целое число cosx = — -

х₂ = arccos (—1 ) + 2лк = ± 27 +

2лк, где к — целое число

• б) . Корни, принадлежащие отрезку [-2π; - π], найдем геометрическим методом с помощью единичной окружности (рис.1).

  

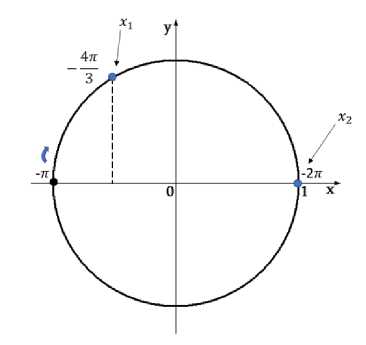
  рис.1

  
  

л   4л

• х1 = —л — з = — у

• х2 = —2л

Ответ: а). х1 = 2лг, где n — целое число, х2 = ±27 + 2лк, где к — целое число. б). Х1 = ——, х2 = —2л.

Часто множество корней тригонометрического уравнения задается некоторым алгебраическим выражением f(n) от одной переменной г Е Z , а заданное множество промежутком с концами а и b (a

Пример 2:

а) . Решите уравнение 4(sin х )2 — 12sinx + 5 = 0 б) . Найдите корни этого уравнения, принадлежащие промежутку:

[-п; 2п].

Решение:

• а) . Обозначим sinx = t, где — 1 < t < 1, тогда 4t 2 - 12t +5 = 0. Решаем данное квадратное уравнение: D = Ь² — 4ас = (—12)2 — 4 • 4 • 5 = 144 — 80 = 64.

_ —Ь + VD _ —(—12) + V64 _ 12 + 8 _ 20 _ 5 _

= 2а =     2^4     =   8   = "в" = 2 = 2,5

t₁ - не является корнем уравнения, так как не принадлежит промежутку

[-1; 1].

—Ь — VD   —(—12) — V64  12 — 8  4  1

2а =     2^4    =  8  = 8 = 2

Обратная замена: sinx = |

х1

= arcsin

+ 2лп = - + 2лп, где n - целое число

х2 = п — arcsin (1 ) + 2лк = л — - + 2лк = 5- + 2лк, где к - целое число.

• б) . Найдем корни уравнения, принадлежащие промежутку [-п; 2п],

алгебраическим методом.

Решаем неравенство —л < - + 2лп < 2л 1                           6

—л — — < 2лп < 2л — — 66

— 7л<2лп<11л

Разделим это неравенство на —, получим:

11 < п < —

Так как n является целым числом, то n=0. Отсюда находим хт = - +

2л • 0 = —.

Аналогично решаем следующее неравенство —л < — + 2лк <  2л

—л — ^ < 2лк < 2л — 5л

6                 6

11л

""6""

< 2лк

7л < —

Разделим это неравенство на —, получим:

Г2<к

< —-

Так как k является целым числом, то k=0. Отсюда находим х2 = — +

2л • 0 = —.

Ответ: а). х1 = — + 2лп , где n — целое число. х₂ = 5— + 2лк, где к — целое число. б). х 1 = — х₂ = -—.

Зачастую формула корней тригонометрического уравнения является линейной возрастающей функцией f(n) от одной переменной n G Z, а промежуток представляет из себя отрезок [a;b], где a

f(i) (i G N U 0) удовлетворяет неравенству a < /(i) < b. Если же 2). a < /(0) < b, то находим поочередно f(1), f(2), . , f(-1), f(-2), . и определяем, какие из чисел f(i) (i G Z) удовлетворяют неравенству a

< /(i) < b. Наконец, если 3). b

находим такие числа f(-i) (i G N), что a < /(—i) < b [3]. Данный метод отбора корней из заданного множества называется функциональный.

Рассмотрим данный метод на примере 3.

Пример 3:

а) . Решите уравнение 7 cos (5^ + x) — 2cos2x = 0 б) . Найдите все корни данного уравнения, принадлежащие отрезку [5п; 6п] [4].

Решение:

• а) . Воспользуемся формулой приведения и формулой двойного угла cos2x = 1 — 2 (sinx)² для преобразования левой части данного уравнения:

—7sinx — 2(1 — 2(sinx)2) = 0

—7sinx + 4(sinx)2 — 2 = 0

4(sinx)2 — 7sinx — 2 = 0

Обозначим sinx = t, где —1 < t < 1, тогда 4t² - 7t -2 = 0

Решаем данное квадратное уравнение: D = b2 — 4ac = (—7)2 — 4 • 4-(—2) = 49 + 32 = 81.

_ —b + VD _ —(—7) + V81 _ 7 + 9 _ 16 _

f1 = 2a  =    2;    =  8  = T =2

t₁- не является корнем уравнения, так как не принадлежит промежутку

[-1; 1].

—b — VD —(—7) — V81  7 — 9    2    1

2a =    2-4    =  8  = — 8 = —4

Обратная замена: sinx = — ~

xi

= arcsin

(—4)

+ 2лп =

— arcsin

+ 2лп , где n - целое число

x2 = п — (—arcsin (1 )) + 2лк = л + arcsin (1 ) + 2лк, где к - целое число.

Полученные корни уравнения можно представить следующим образом: х = (—1)^m+1 • arcsin (1) + пт, где тЕ Z.

• б) . Найдем все корни данного уравнения, принадлежащие отрезку

[5π; 6π], функциональным методом.

Запишем множество х = (—1)m+1 • arcsin (1) + пт, где т Е Z в виде двух

множеств: х1 = — arcsin (1) + 2un, где n

–

целое число.

х2 =

n=0

и + arcsin (1 ) + 2ик , где к — целое число.

Функция х1 является линейно возрастающей функцией от n и при принимает отрицательное значение — arcsin (1) . Поэтому все значения х1 при n = 0; -1; -2 .. будут меньше 5п и в заданный промежуток не попадают.

Находим

значение х1

при

n=1.

Получаем

число 2п — arcsin (1). 2п — arcsin (1) < 5п. То есть значение х1 при n=1

не входит в заданный промежуток.

Находим

значение х1

при

n=2.

Получаем

число 4п — arcsin (1). 4п — arcsin (1) < 5п. То есть значение х1 при n=2

не входит в заданный промежуток.

Находим значение х₁ при n=3. Получаем число 6и — arcsin (1) .

5u < 6u — arcsin (1) < 6и. То есть 6п — arcsin (1) попадает в заданный промежуток.

Далее убеждаемся, что значение х1 при n=4 больше 6п. Получаем число 8п — arcsin (1) > 6п. То есть значение х1 при n=4 не входит в заданный промежуток.

Единственное значение при  х1 = 6л — arcsin (1) попадает в заданный промежуток.

Аналогично рассуждая, получаем, что функция х₂ является линейно возрастающей функцией от k и при k=0 принимает положительное значение л + arcsin (1 ), меньшее 5 л. Поэтому все значения х₂ при k = 0; -1; -2 … будут меньше 5π и в заданный промежуток не попадают.

Находим

значение

х2

при

k=1.

Получаем

число 3л + arcsin (1). 3л + arcsin (1) < 5п. То есть значение х₂ при k=1 не входит в заданный промежуток.

Находим значение х2 при k=2. Получаем число 5л + arcsin (1) . 5л < 5л + arcsin (1) < 6л. То есть 5л + arcsin (1) попадает в заданный промежуток.

Теперь убеждаемся, что значение х₂ при k=3 больше 6л. Получаем число 7л + arcsin (1) > 6л. То есть значение х₂ при k=3 не входит в заданный промежуток.

Значит, единственное значение при х2 = 5л + arcsin (1) попадает в заданный промежуток.

Ответ: а). х = (—1)m+1 • arcsin (1) + лт, где т Е Z б). х1 = 6л — arcsin (1), х2 = 5л + arcsin (1) .

Таким образом, отобрать корни в тригонометрическом уравнении из заданного множества можно, как минимум, тремя методами: геометрически, алгебраически, функционально. Для конкретного множества можно подобрать более рациональный способ. Эти методы можно использовать при решении задач единого государственного экзамена по профильной математике.