Методы применения матриц при создании моделей группового преследования

Original article

Methods for Applying Matrices when Creating Models of Group Pursuit

Alexander A. Dubanov

Introduction. It is obvious that in the near future, the issues of equipping moving robotic systems with autonomous control elements will remain relevant. This requires the development of models of group pursuit. Note that optimization in pursuit tasks is reduced to the construction of optimal trajectories (shortest trajectories, trajectories with differential constraints, fuel consumption indicators). At the same time, the aspects of automated distribution by goals in group pursuit were not considered. To fill this gap, the presented piece of research has been carried out. Its result should be the construction of a model of automated distribution of pursuers by goals in group pursuit.

Materials and Methods. A matrix was formed to study the multiple goal group pursuit. The control parameters for the movement of the pursuers were modified according to the minimum curvature of the trajectory. The methods of pursuit and approach were considered in detail. The possibilities of modifying the method of parallel approach were shown. Matrix simulation was used to build a scheme of multiple goal group pursuit. The listed processes were illustrated by functions in the given coordinate systems and animation. Block diagrams of the phase coordinates of the pursuer at the next step, the time and distance of the pursuer reaching the goal were constructed as a base of functions. In some cases, the location of targets and pursuers was defined as points on the circle of Apollonius. The matrix was formed by samples corresponding to the distribution of pursuers by goals.

Results . Nine variants of the pursuit, parallel, proportional and three-point approach on the plane and in space were considered. The maximum value of the goal achievement time was calculated. There were cases when the speed vector of the pursuer was directed arbitrarily and to a point on the Apollonius circle. It was noted that the three-point approach method was convenient if the target was moving along a ballistic trajectory. To modify the method of parallel approach, a network of parallel lines was built on the plane. Here, the length of the arc of the line (which can be of any shape) and the array of reference points of the target trajectory were taken into account. An equation was compiled and solved with these elements. On an array of samples with corresponding time values, the minimum time was found, i.e., the optimal time for simultaneous group achievement of multiple goals was determined. For unified access to the library, the control vector was expressed through a one-parameter family of parallel planes. A library of calculations of control vectors was formed. An example of applying matrix simulation to group pursuit was shown. A scheme of group pursuit of multiple goals was presented. For two goals and three pursuers, six samples corresponding to the distribution of pursuers by goals were considered. The data was presented in the form of a matrix. Based on the research results, the computer program was created and registered – “Parallel Approach on Plane of Group of Pursuers with Simultaneous Achievement of the Goal”.

Введение. Алгоритмы преследования изучаются с точки зрения их классической и оптимальной реализации. Исследуется их роль в дифференциальных играх преследования. Прикладная сфера готовых решений весьма широка, т. к. результаты таких научных изысканий применимы в различных информационных технологиях и системах, в частности в поисковых. Безусловно также, что продолжительное время будут актуальны вопросы оснащения движущихся робототехнических комплексов элементами автономного управления, что также требует качественной реализации рассматриваемых алгоритмов.

В работах [1–4] исследовалось согласованное поведение группы преследователей и целей. Для общих теоретических и практических вопросов в задачах преследования рассматривались работы [5–9]. Наведение преследователя на цель анализировалось в свете информации, представленной в [10–13].

При всем теоретическом и практическом интересе к данной теме оптимизация в задачах преследования ограничивается построением оптимальных траекторий. Предлагаются, например, кратчайшие траектории, траектории с дифференциальными ограничениями, показатели расхода топлива. Но не рассматриваются аспекты автоматизированного распределения по целям при групповом преследовании. Для восполнения этого пробела проводилась данная научная работа. Ее главным результатом представляется построение модели автоматизированного распределения преследователей по целям в групповом преследовании. Показано формирование матрицы достижения преследователями целей. При назначении преследователям целей выполняется перебор всех возможных комбинаций достижения целей и выбирается комбинация минимального значения критерия из формируемого множества с максимальным значением.

Оптимизация группового преследования множества целей является перспективным направлением развития такой дисциплины, как оптимальное управление движением в задачах, связанных с автоматизированным принятием решений и автономным управлением.

Материалы и методы. В модели описанного в статье группового преследования цели движутся по предопределенным траекториям. Однако эта предопределенность не имеет принципиального значения. Преследователи распределяются по целям автоматически, на основе минимаксного решения целевой функции. Затем модифицируются управляющие параметры движения преследователей. В данной работе это параметр минимальной кривизны траектории. Такой подход позволяет обеспечить одновременное достижения целей.

Рассмотрим групповое преследование множества целей: N преследователей догоняют M целей. Сформируем матрицу распределения преследователей по целям:

¥.„ гдеi = 1.. N , j = 1.. M .

ij

Каждая ячейка V j содержит информацию о фазовых координатах i -го преследователя и j -й цели. В матрице V у содержится информация о том, каким методом i -й преследователь преследует j -ю цель.

Данные, хранящиеся в ячейках матрицы, определяют обращение к библиотеке расчетов управляющих векторов преследователя.

В каждой ячейке матрицы V j может рассчитываться прогнозируемое время достижения i-м преследователем j-й цели: tij.

Результаты работы

В каждой полученной выборке  Ak ={vit^...Т^^} следует найти максимальное значение времен достижений tk = Max{ttJ} , например из {t2,,t23,t32,t4J (таблица 1).

Информатика , вычислительная техника и управление

Таблица 1

Выборки, соответствующие распределению преследователей по целям

1 c

Цели

1

2

1

2

1

2

1

2

1

2

1

2

1

×

×

×

×

×

×

2

×

×

×

×

×

×

3

×

×

×

×

×

×

Выборки

Л 1

^ 2

^ 3

^ 4

a 5

A 6

Необходимо сформировать матрицы Ψ ij , где i = 1… 3 , j =1… 2 в соответствии с возможными выборками A k ,k = 1…6. Затем, после обращения находится максимальное значение t k =Max{ t ij }. Расчет позволил установить, что наибольшее время достижения демонстрирует преследователь P 1 , настигающий цель T 1 из выборки A 2 .

Итак, рассмотрим выборку A k . Можно увеличить до значения параметра t k все значения t ij , зависящие от векторов скоростей преследователей и целей, а также их допустимых угловых скоростей. Этим определяется максимальное значение t k .

Получив массив выборок { A k } с соответственными значениями времен { t ij }, следует найти минимальное время t min = Min { t k }. Так определяется оптимальное время одновременного группового достижения множества целей.

Алгоритмы расчета следующего шага преследователя и оценки времени достижения преследователем цели. На рис. 1 представлен алгоритм функции расчета следующего шага и вектора скорости движения преследователя.

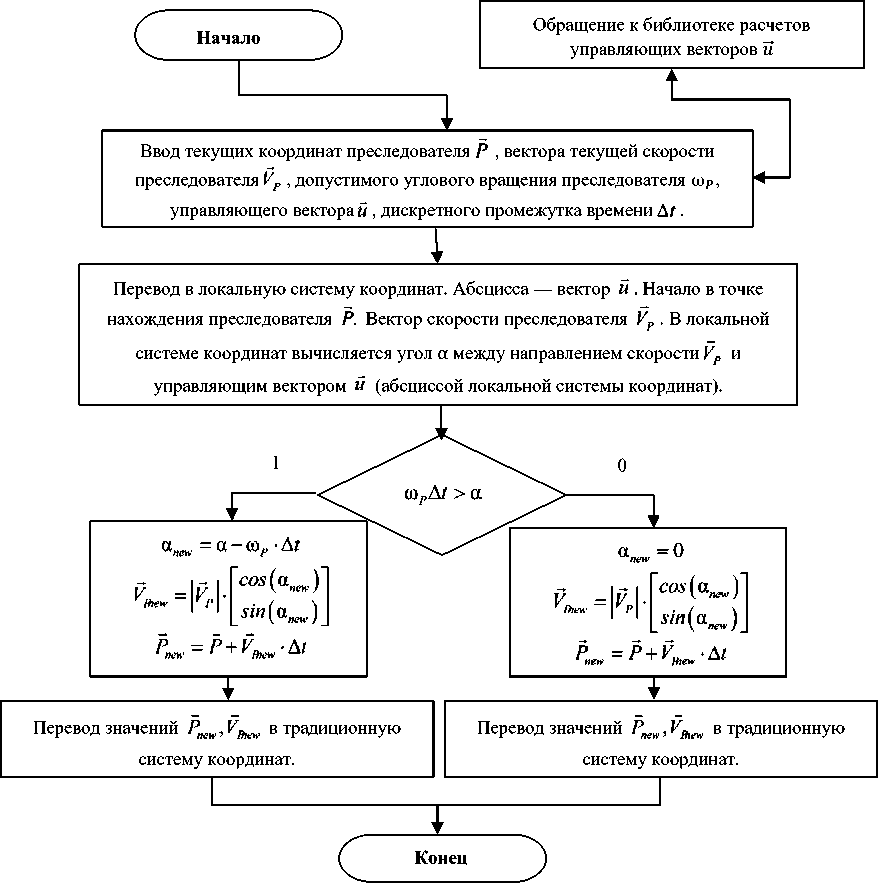
Рис. 1. Блок-схема расчета фазовых координат преследователя на следующем шаге

На рис. 2 представлен алгоритм расчета времени и расстояния достижения преследователем цели. Переменная 8 — это пороговое значение расстояния от преследователя до цели, при достижении которого цель считается достигнутой.

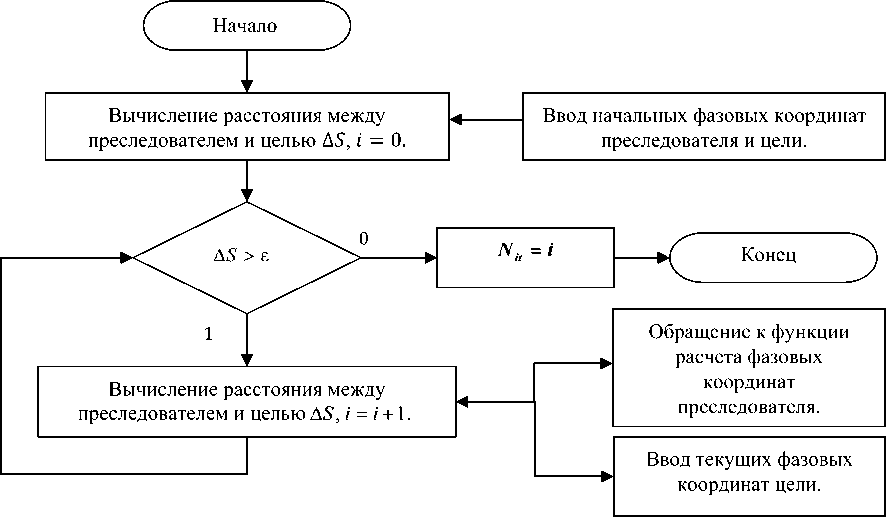
Рис. 2. Блок-схема функции расчета времени и расстояния достижения преследователем цели

Если цель движется по предопределенной траектории, то алгоритм, представленный на рис. 2, может дать оценку времени t ij достижения i -м преследователем j -й цели. В этом случае выходным параметром функции может служить количество итераций процесса преследования N it . Количество итераций N it — выходной параметр функции расчета времени и расстояния достижения преследователем цели.

Если цель предпринимает ответные шаги, чтобы избежать достижения, следует оценивать время иначе. Нужно строить прогнозируемые траектории как составные из сегментов прямых, дуг окружностей, квадратных и кубических парабол и других известных линий. Это позволит не решать краевые задачи в расчетном цикле.

Формирование библиотеки расчетов управляющих векторов. Матрица распределения ¥ ij , где i = 1... N, j =1… M преследователей по целям будет строиться на каждом дискретном промежутке времени. В каждой ячейке матрицы ¥ ij будет храниться информация о методе преследования. На ней основывается обращение к библиотеке функций расчета управляющих векторов и (рис. 3-11).

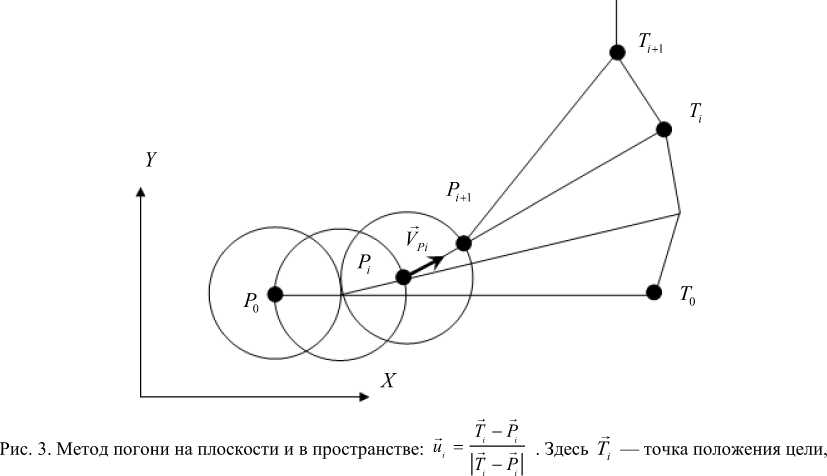
P — точка положения преследователя [14]

, вычислительная техника и управление

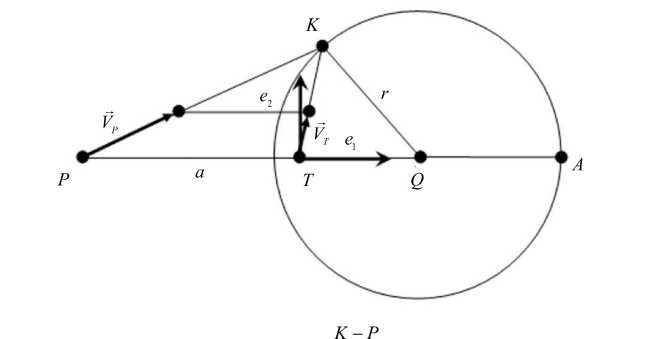
Рис. 4. Метод параллельного сближения на плоскости: и = ------- . T — точка положения цели, P — точка положения

I K - P

преследователя, K — точка на окружности Аполлония.

Она однозначно определена точками P , T и вектором скорости цели V [15]

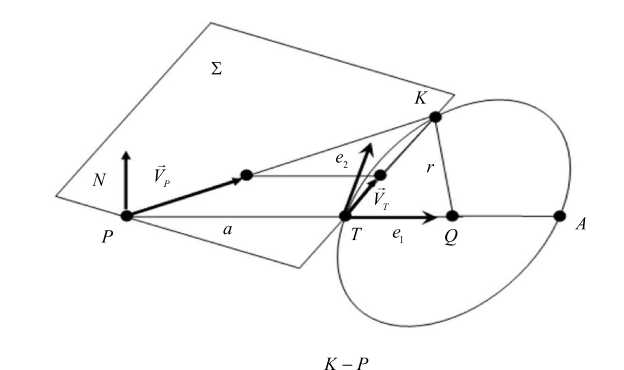
Рис. 5. Метод параллельного сближения в пространстве: и = ------- , T — точка положения цели, P — точка положения

IK - P преследователя, K — точка на окружности Аполлония. Окружность Аполлония лежит в плоскости 2, образованной точками P, T и вектором скорости цели VT [16]. Показан случай, когда вектор скорости преследователя направлен произвольно. По истечении некоторого времени вектор скорости преследователя направлен в точку на окружности Аполлония

f ( x,y ) .

X

P i

P i + 1

W + 1

L i + 1

S i + 1

*

¹ i + 1

*

P i + 1

T + 1

P i ^*

L i

T ^*

S i

W i      T i

Z

Y

P i + 1 - P i

, где P — результат пересечения поверхности z=f ( x,y ), плоскости

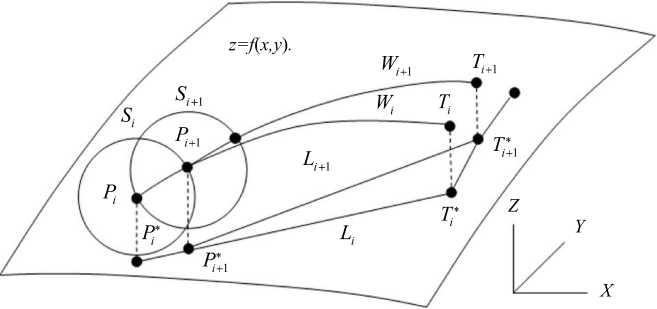
Рис. 6. Метод погони на поверхности: и, = :--------г

I P ? + 1 - P i l

PP*T и сферы S i с центром в точке P i . Радиус ^_г | • A t . Точка P* — ортогональная проекция точки P i на плоскость XY .

Для унифицированного обращения к библиотеке необходимо выразить управляющий вектор [17]

ф

P i

P z=F(x,y)

P i + 1 - Р

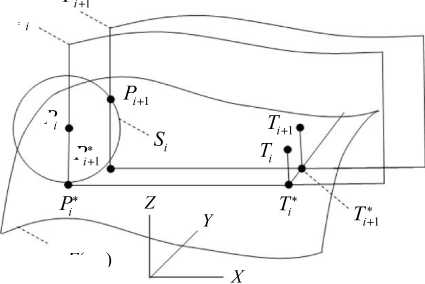
Рис. 7. Метод параллельного сближения на поверхности: и =  ----- . Здесь Р . +1 — результат пересечения поверхности

'   |Р+1 -Р z=f (x,y), плоскости Р+1Р+Т+1 и сферы S. с центром в точке Р.. Радиус | V | • At .

Точка Р+1 — ортогональная проекция точки Р. +1 на плоскость XY. Для унифицированного обращения к библиотеке необходимо выразить управляющий вектор. Ф. — однопараметрическое семейство параллельных плоскостей [18]

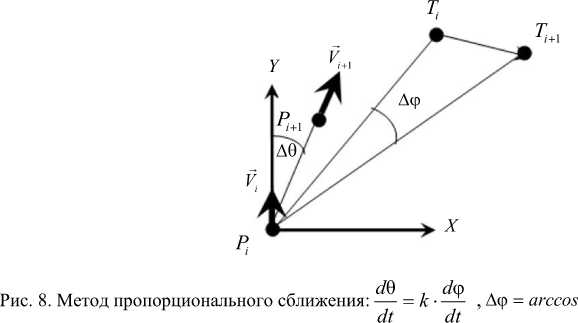
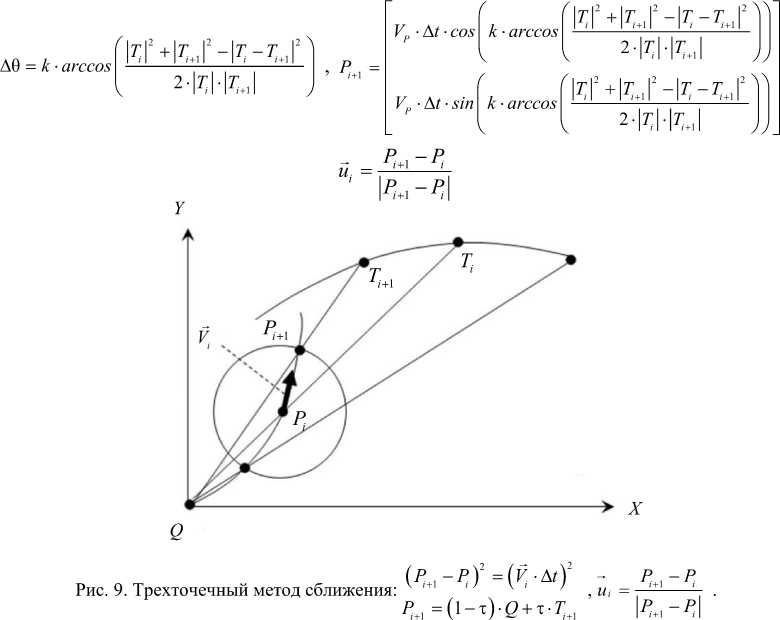
Метод удобен, если цель движется по баллистической траектории

., вычислительная техника и управление

Ри

К

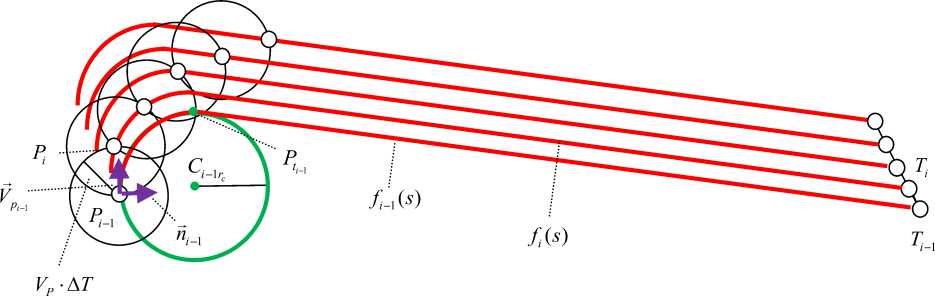
Рис. 10. Модификация метода параллельного сближения на плоскости. Строится сеть параллельных линий fu 1 (s) = f (s) + T.+1 - T , где s — длина дуги линии, Ti — массив опорных точек траектории цели. Решение уравнения ( f+1 ( s )-P )2 =( VP'A t )2 относительно параметра s позволит найти значение s*, которое будет соответствовать

P + i = f + i ⁽ s * ) .

P 1 - P u = i------i

'     I P ? + 1 - P l

В семействе f i (s) могут быть линии произвольной конфигурации[19]

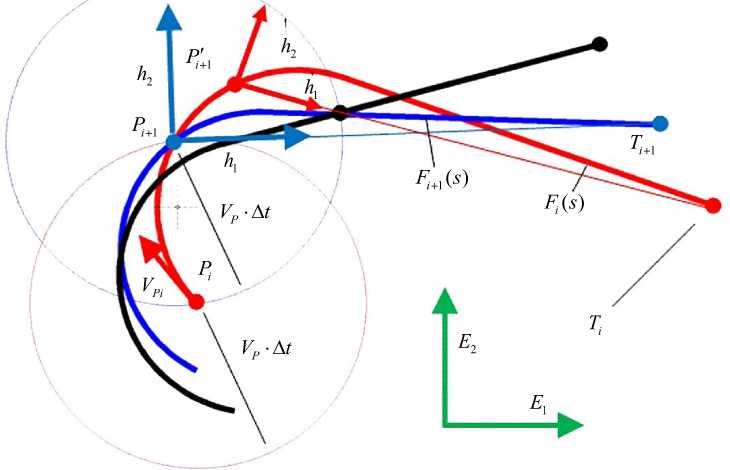
Рис. 11. Модификация метода погоней на плоскости. Строится сеть f i (s), где s — длина дуги линии, T i — массив опорных точек траектории цели. Выполняется условие, что конец линии f i (s) проходит через точку T i , а точка

P i инцидентна линии f t (s), то есть используется в качестве лекала. Решение уравнения ( f _+т ( s ) - P ) 2 = ( V_p - A t ) 2

относительно параметра s позволит найти значение s ^*, которое будет соответствовать P

= ^f + 1 ( ^s *) . u i

^Pi + 1 - P

I P + 1 - P ? l ■

В семействе f i (s) могут быть линии произвольной конфигурации [20]

Итак, библиотека расчетов управляющих векторов содержит методы погони на плоскости, в пространстве и на поверхности. Методы параллельного сближения рассчитываются на плоскости, в пространстве и на поверхности. Методы пропорционального сближения рассчитываются на плоскости и в пространстве. Трехточечные методы рассчитываются на плоскости и в пространстве. Модифицированные методы погони рассчитываются на плоскости и в пространстве, когда для управления преследователем задействуют допустимую кривизну траекторий. Модифицированные методы параллельного сближения рассчитываются на плоскости и в пространстве.

Модификация методов параллельного сближения и погони позволяет строить сеть прогнозируемых траекторий, которые допускают различные краевые условия. Это иллюстрируют рис. 3–11. Но на них представлены далеко не все методы расчета управляющих векторов. Подразумевается, что это открытая, пополняемая библиотека функций.

Пример применения матричного моделирования к групповому преследованию. Рассмотрим пример группового преследования (рис. 12).

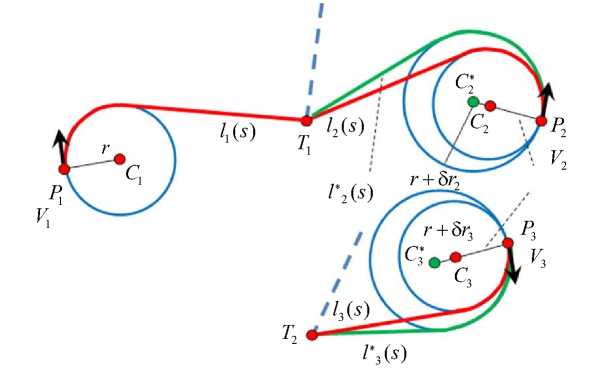
Рис. 12. Схема группового преследования множества целей

Здесь все преследователи достигают цели по модифицированному методу параллельного сближения, что соответствует рис. 10. В модели преследования на. рис. 10 кривизна траектории не должна быть больше определенного значения. Поэтому у преследователей P ₂ и P ₃ увеличивается первоначальный радиус кривизны траектории, что показано на рис. 12.

Сформирована выборка A k , в которой преследователь P i догоняет T j. Далее происходит первичная оценка времени достижения t ij . Для оценки времени t ij вычисляются:

• -    длина прямолинейного участка до цели,

• -    длина дуги сопрягаемой окружности допустимого радиуса.

Затем выбирается максимальное значение t k = Max { t ij }. Увеличение времени t ij до t k в данной модели происходит за счет увеличения у преследователя P i радиуса сопрягаемой окружности со значения r i до значения r i + 5 r i.

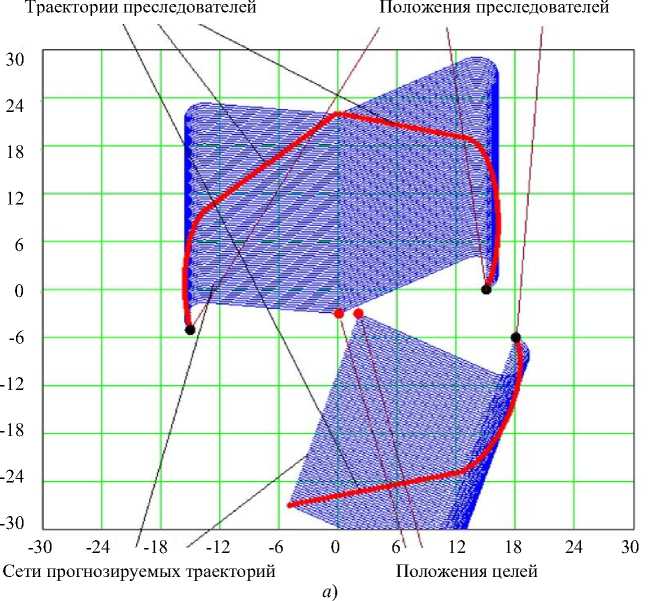
Рис. 13 дополнен анимированным изображением, где показан процесс группового преследования множества целей [21].

Информатика , вычислительная техника и управление

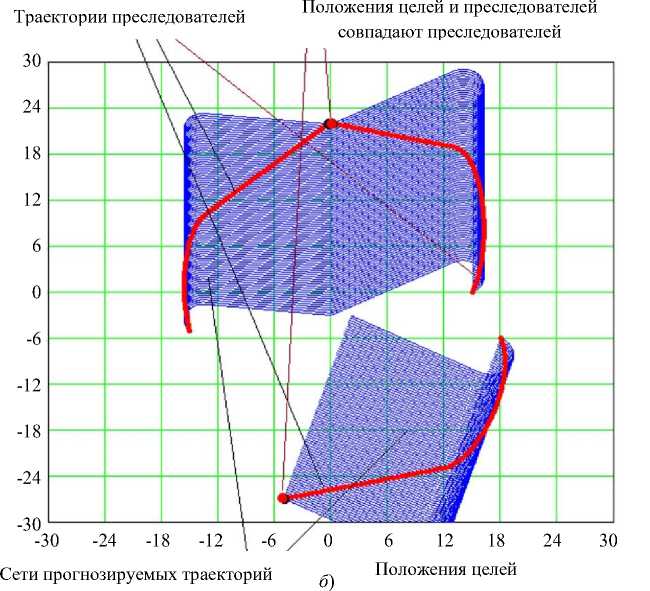
Рис. 13. Схемы фаз группового преследования: а — начальная фаза; б — конечная фаза

По результатам исследования создана и зарегистрирована программа для ЭВМ [22], которая реализует алгоритм группового преследования нескольких целей. Это софтверное решение называется «Модель параллельного сближения на плоскости группы преследователей с одновременным достижением цели».

Обсуждение и заключение. Описаны и визуализированы в виде функций на плоскости, на поверхности и в пространстве методы погони, параллельного, пропорционального и трехточечного сближения. Кроме того, показаны возможности модификации метода параллельного сближения на плоскости. С применением матричного моделирования к групповому преследованию выстраивается схема группового преследования множества целей. Отдельно показаны начальная и конечная фаза этого процесса. Расчет времени достижения позволил выявить преследователя, которому нужно наибольшее время, чтобы настичь цель из рассматриваемой выборки.

Итак, предполагается, что матрица распределения преследователей по целям будет генерироваться в каждый момент времени. Цели и преследователи могут исчезать, могут появляться новые. Такая матрица может использоваться и стороной, представляющей цели, которая уклоняется от преследования. Итоги описанных в статье научных изысканий позволят сформировать принципы автоматизированного распределения преследователей по целям на основе выбранной целевой функции. Предлагаются алгоритмы модификации траекторий преследователей для достижения целей одновременно или согласно установленному графику. Также рассматриваются вопросы формирования библиотеки методов преследования. Метод формирования матрицы распределения преследователей по целям может быть востребован при проектировании систем виртуальной реальности для игровых задач, в которых моделируется процесс группового преследования, убегания и уклонения.

Список литературы